1.4E: Exercícios para a Seção 1.4
- Page ID
- 188658
Nos exercícios 1 a 6, use o teste de linha horizontal para determinar se cada um dos gráficos fornecidos é individual.
1)
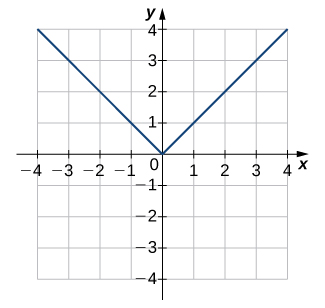
- Resposta
- Não um para um
2)
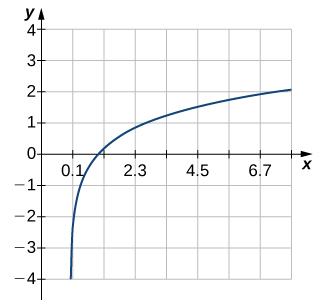
3)
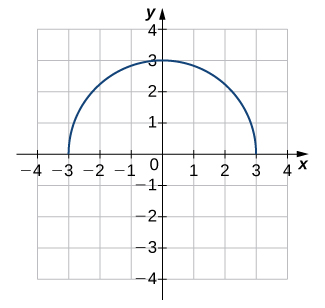
- Resposta
- Não um para um
4)
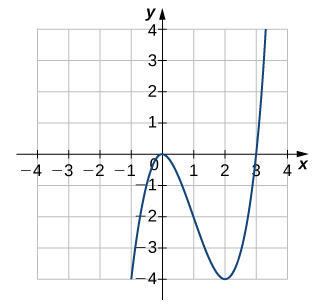
5)
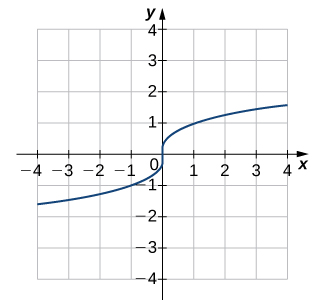
- Resposta
- Um para um
6)
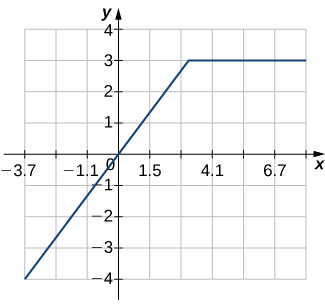
Nos exercícios 7 a 12,
a. encontre a função inversa e
b. encontre o domínio e o alcance da função inversa.
7)\(f(x)=x^2−4, \quad x≥0\)
- Resposta
- a.\(f^{−1}(x)=\sqrt{x+4}\)
b. Domínio:\(x≥−4,\) Intervalo:\(y≥0\)
8)\(f(x)=\sqrt[3]{x−4}\)
9)\(f(x)=x^3+1\)
- Resposta
- a.\(f^{−1}(x)=\sqrt[3]{x−1}\)
b. Domínio: todos os números reais, Intervalo: todos os números reais
10)\(f(x)=(x−1)^2, \quad x≤1\)
11)\(f(x)=\sqrt{x−1}\)
- Resposta
- a.\(f^{−1}(x)=x^2+1\),
b. Domínio:\(x≥0,\) Intervalo:\(y≥1\)
12)\(f(x)=\dfrac{1}{x+2}\)
Nos exercícios 13 a 16, use o gráfico de\(f\) para esboçar o gráfico de sua função inversa.
13)
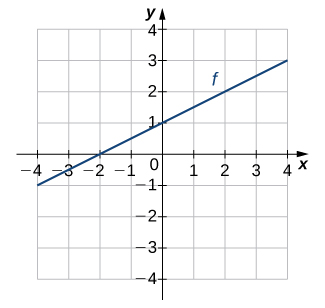
- Resposta
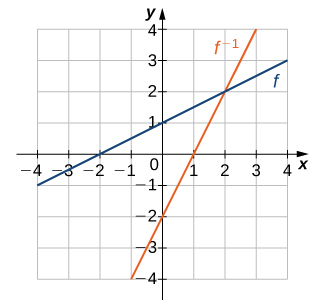
14)
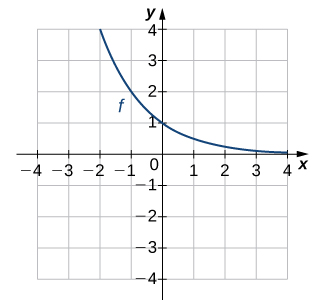
15)
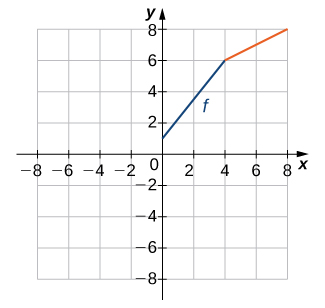
- Resposta
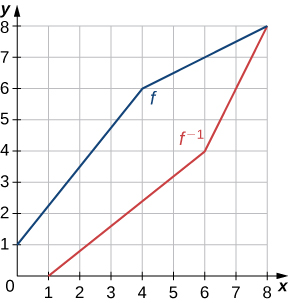
16)
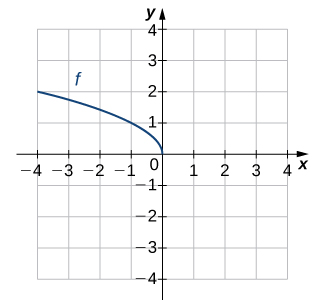
Nos exercícios 17 a 24, use a composição para determinar quais pares de funções são inversas.
17)\(f(x)=8x, \quad g(x)=\dfrac{x}{8}\)
- Resposta
- São inversas.
18)\(f(x)=8x+3, \quad g(x)=\dfrac{x-3}{8}\)
19)\(f(x)=5x−7, \quad g(x)=\dfrac{x+5}{7}\)
- Resposta
- Não são inversas.
20)\(f(x)=\frac{2}{3}x+2, \quad g(x)=\frac{3}{2}x+3\)
21)\(f(x)=\dfrac{1}{x−1}, \;x≠1, \quad g(x)=\dfrac{1}{x}+1,\; x≠0\)
- Resposta
- São inversas.
22)\(f(x)=x^3+1,\quad g(x)=(x−1)^{1/3}\)
23)\(f(x)=x^2+2x+1,\; x≥−1, \quad g(x)=−1+\sqrt{x},\; x≥0\)
- Resposta
- São inversas.
24)\(f(x)=\sqrt{4−x^2},\; 0≤x≤2, \quad g(x)=\sqrt{4−x^2},\; 0≤x≤2\)
Nos exercícios 25 a 33, avalie as funções. Dê o valor exato.
25)\(\tan^{−1}\left(\frac{\sqrt{3}}{3}\right)\)
- Resposta
- \(\frac{π}{6}\)
26)\(\cos^{−1}\left(−\frac{\sqrt{2}}{2}\right)\)
27)\(\cot^{−1}(1)\)
- Resposta
- \(\frac{π}{4}\)
28)\(\sin^{−1}(−1)\)
29)\(\cos^{−1}\left(\frac{\sqrt{3}}{2}\right)\)
- Resposta
- \(\frac{π}{6}\)
30)\(\cos\big(\tan^{−1}(\sqrt{3})\big)\)
31)\(\sin\left(\cos^{−1}\left(\frac{\sqrt{2}}{2}\right)\right)\)
- Resposta
- \(\frac{\sqrt{2}}{2}\)
32)\(\sin^{−1}\left(\sin\left(\frac{π}{3}\right)\right)\)
33)\(\tan^{−1}\left(\tan\left(−\frac{π}{6}\right)\right)\)
- Resposta
- \(-\frac{π}{6}\)
34) A função\(C=T(F)=(5/9)(F−32)\) converte graus Fahrenheit em graus Celsius.
a) Encontre a função inversa\(F=T^{−1}(C)\)
b) Para que serve a função inversa?
35) [T] A velocidade\(V\) (em centímetros por segundo) do sangue em uma artéria a uma distância\(x\) cm do centro da artéria pode ser modelada\(V=f(x)=500(0.04−x^2)\) pela função de\(0≤x≤0.2.\)
a) Encontre\(x=f^{−1}(V).\)
b) Interprete para que a função inversa é usada.
c) Encontre a distância do centro de uma artéria com uma velocidade de 15 cm/seg, 10 cm/seg e 5 cm/seg.
- Resposta
- a.\(x=f^{−1}(V)=\sqrt{0.04−\dfrac{V}{500}}\)
b. A função inversa determina a distância do centro da artéria na qual o sangue está fluindo com velocidade\(V.\)
c. 0,1 cm; 0,14 cm; 0,17 cm
36) Uma função que converte tamanhos de vestidos nos Estados Unidos para os da Europa é dada por\(D(x)=2x+24.\)
a) Encontre os tamanhos de vestidos europeus que correspondem aos tamanhos 6, 8, 10 e 12 nos Estados Unidos.
b) Encontre a função que converte tamanhos de vestidos europeus em tamanhos de vestidos dos EUA.
c) Use a parte b. para encontrar os tamanhos de vestido nos Estados Unidos que correspondem a 46, 52, 62 e 70.
37) [T] O custo para remover uma toxina de um lago é modelado pela função\(C(p)=\dfrac{75p}{85−p},\) onde\(C\) está o custo (em milhares de dólares) e\(p\) é a quantidade de toxina em um pequeno lago (medida em partes por bilhão [ppb]). Este modelo é válido somente quando a quantidade de toxina é inferior a 85 ppb.
a) Encontre o custo para remover 25 ppb, 40 ppb e 50 ppb da toxina do lago.
b) Encontre a função inversa.
c) Use a parte b. para determinar quanto da toxina é removida por $50.000.
- Resposta
- a. $31.250, $66.667, $107.143
b.\(p=\dfrac{85C}{C+75}\)
c. 34 ppb
38) [T] Um carro de corrida está acelerando a uma velocidade dada por\(v(t)=\frac{25}{4}t+54,\)
onde\(v\) está a velocidade (em pés por segundo) no momento\(t.\)
a) Encontre a velocidade do carro em 10 segundos.
b) Encontre a função inversa.
c) Use a parte b. para determinar quanto tempo o carro leva para atingir uma velocidade de 150 pés/seg.
39) [T] O número Mach de um avião\(M\) é a razão entre sua velocidade e a velocidade do som. Quando um avião está voando a uma altitude constante, seu ângulo de Mach é dado por\(μ=2\sin^{−1}\left(\frac{1}{M}\right).\)
Encontre o ângulo de Mach (até o grau mais próximo) para os seguintes números de Mach.
1.0”." style="width: 465px; height: 305px;" width="465px" height="305px" src="https://math.libretexts.org/@api/dek...01_04_215.jpeg">
uma.\(μ=1.4\)
b.\(μ=2.8\)
c.\(μ=4.3\)
- Resposta
- a.\(\sim 92°\) b.\(\sim 42°\) c.\(\sim 27°\)
40) [T] Usando\(μ=2\sin^{−1}\left(\frac{1}{M}\right)\), encontre o número Mach M para os seguintes ângulos.
uma.\(μ=\frac{π}{6}\)
b.\(μ=\frac{2π}{7}\)
c.\(μ=\frac{3π}{8}\)
41) [T] A temperatura (em graus Celsius) de uma cidade no norte dos Estados Unidos pode ser modelada pela função
\(T(x)=5+18\sin\left[\frac{π}{6}(x−4.6)\right],\)
onde\(x\) está o tempo em meses e\(x=1.00\) corresponde a 1º de janeiro. Determine o mês e o dia em que a temperatura é\(21°C.\)
- Resposta
- \(x≈6.69,\, 8.51\); então, a temperatura ocorre em 21 de junho e 15 de agosto
42) [T] A profundidade (em pés) da água em uma doca muda com o aumento e a queda das marés. É modelado pela função em\(D(t)=5\sin\left(\frac{π}{6}t−\frac{7π}{6}\right)+8,\) que\(t\) é o número de horas após a meia-noite. Determine a primeira vez depois da meia-noite quando a profundidade é de\(11.75\) pés.
43) [T] Um objeto que se move em movimento harmônico simples é modelado pela função em\(s(t)=−6\cos\left(\dfrac{πt}{2}\right),\) que\(s\) é medido em polegadas e\(t\) é medido em segundos. Determine a primeira vez em que a distância percorrida está\(4.5\) dentro.
- Resposta
- \(\sim 1.5\)seg
44) [T] Uma galeria de arte local tem um retrato de 3 pés de altura pendurado 2,5 pés acima do nível dos olhos de uma pessoa comum. O ângulo de visão\(θ\) pode ser modelado pela função\(θ=\tan^{−1}\frac{5.5}{x}−\tan^{−1}\frac{2.5}{x}\), onde\(x\) está a distância (em pés) do retrato. Encontre o ângulo de visão quando uma pessoa estiver a 4 pés do retrato.
45) [T] Use uma calculadora para avaliar\(\tan^{−1}(\tan(2.1))\)\(\cos^{−1}(\cos(2.1))\) e. Explique os resultados de cada um.
- Resposta
- \(\tan^{−1}(\tan(2.1))≈−1.0416\); a expressão não é igual,\(2.1\) pois\(2.1>1.57=\frac{π}{2}\) — em outras palavras, ela não está no domínio restrito de\(\tan x\). \(\cos^{−1}(\cos(2.1))=2.1\), já que\(2.1\) está no domínio restrito de\(\cos x\).
46) [T] Use uma calculadora para avaliar\(\sin(\sin^{−1}(−2))\)\(\tan(\tan^{−1}(−2))\) e. Explique os resultados de cada um.


