1.4: Funções inversas

objetivos de aprendizagem

• Determine as condições para quando uma função tem um inverso.
• Use o teste de linha horizontal para reconhecer quando uma função é individual.
• Encontre o inverso de uma determinada função.
• Desenhe o gráfico de uma função inversa.
• Avalie funções trigonométricas inversas.

Uma função inversa reverte a operação realizada por uma função específica. Em outras palavras, o que quer que uma função faça, a função inversa a desfaz. Nesta seção, definimos formalmente uma função inversa e declaramos as condições necessárias para que uma função inversa exista. Examinamos como encontrar uma função inversa e estudamos a relação entre o gráfico de uma função e o gráfico de sua inversa. Em seguida, aplicamos essas ideias para definir e discutir as propriedades das funções trigonométricas inversas.

Existência de uma função inversa

Começamos com um exemplo. Dada uma função\(f\) e uma saída\(y=f(x)\), geralmente estamos interessados em descobrir qual valor ou valores\(x\) foram mapeados\(y\) por\(f\). Por exemplo, considere a função\(f(x)=x^3+4\). Como qualquer saída\(y=x^3+4\), podemos resolver essa equação\(x\) para descobrir que a entrada é\(x=\sqrt[3]{y−4}\). Essa equação é definida\(x\) como uma função de\(y\). Denotando essa função como\(f^{−1}\), e escrevendo\(x=f^{−1}(y)=\sqrt[3]{y−4}\), vemos isso para qualquer\(x\) pessoa no domínio de\(f,f^{−1}\)\(f(x))=f^{−1}(x^3+4)=x\). Assim, essa nova função\(f^{−1}\), “desfez” o que a função original\(f\) fazia. Uma função com essa propriedade é chamada de função inversa da função original.

Definição: Funções inversas

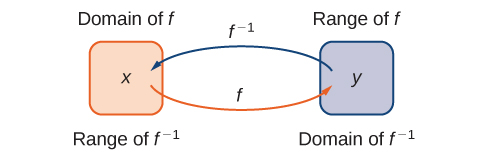
Dada uma função\(f\) com domínio\(D\) e alcance\(R\), sua função inversa (se existir) é a função\(f^{−1}\) com domínio\(R\) e alcance de\(D\) forma que\(f^{−1}(y)=x\) se e somente se\(f(x)=y\). Em outras palavras, para uma função\(f\) e seu inverso\(f^{−1}\),

\[f^{−1}(f(x))=x \nonumber \]

para tudo\(x\) em\(D\) e

\[f(f^{−1}(y))=y \nonumber \]

para todos\(y\)\(R\).

Observe que isso\(f^{−1}\) é lido como “\(f\)inverso”. Aqui, o não\(−1\) é usado como um expoente, então

\[f^{−1}(x)≠ \dfrac{1}{f(x)}. \nonumber \]

A figura\(\PageIndex{1}\) mostra a relação entre o domínio e o intervalo de\(f\) e o domínio e a faixa de\(f^{−1}\).

Figura\(\PageIndex{1}\): Dada uma função\(f\) e seu inverso\(f^{−1},f^{−1}(y)=x\) se e somente se\(f(x)=y\). O intervalo de\(f\) se torna o domínio de\(f^{−1}\) e o domínio de\(f\) se torna o intervalo de\(f^{−1}\).

Lembre-se de que uma função tem exatamente uma saída para cada entrada. Portanto, para definir uma função inversa, precisamos mapear cada entrada para exatamente uma saída. Por exemplo, vamos tentar encontrar a função inversa para\(f(x)=x^2\). Resolvendo a equação\(y=x^2\) para\(x\), chegamos à equação\(x=±\sqrt{y}\). Essa equação não se descreve\(x\) como uma função de\(y\) porque existem duas soluções para essa equação para cada\(y>0\). O problema de tentar encontrar uma função inversa para\(f(x)=x^2\) é que duas entradas são enviadas para a mesma saída para cada saída\(y>0\). A função\(f(x)=x^3+4\) discutida anteriormente não tinha esse problema. Para essa função, cada entrada foi enviada para uma saída diferente. Uma função que envia cada entrada para uma saída diferente é chamada de função individual.

Definição: Funções individuais

Dizemos que uma função\(f\) é uma função individual se\(f(x_1)≠f(x_2)\) quando\(x_1≠x_2\).

Uma forma de determinar se uma função é individual é observando seu gráfico. Se uma função for individual, duas entradas não poderão ser enviadas para a mesma saída. Portanto, se desenharmos uma linha horizontal em qualquer lugar no\(xy\) plano -, de acordo com o teste da linha horizontal, ela não poderá cruzar o gráfico mais de uma vez. Observamos que o teste da linha horizontal é diferente do teste da linha vertical. O teste de linha vertical determina se um gráfico é o gráfico de uma função. O teste de linha horizontal determina se uma função é individual (Figura\(\PageIndex{2}\)).

Teste de linha horizontal

Uma função\(f\) é individual se e somente se cada linha horizontal cruzar o gráfico de\(f\) no máximo uma vez.

Figura\(\PageIndex{2}\): (a) A função não\(f(x)=x^2\) é individual porque falha no teste da linha horizontal. (b) A função\(f(x)=x^3\) é individual porque passa no teste da linha horizontal.

Exemplo\(\PageIndex{1}\): Determining Whether a Function Is One-to-One

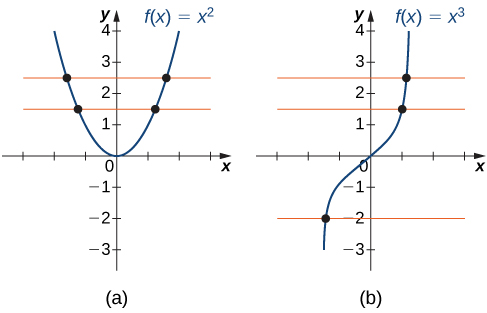
Para cada uma das funções a seguir, use o teste de linha horizontal para determinar se é individual.

uma)

b)

Solução

a) Como a linha horizontal\(y=n\) de qualquer número inteiro\(n≥0\) cruza o gráfico mais de uma vez, essa função não é individual.

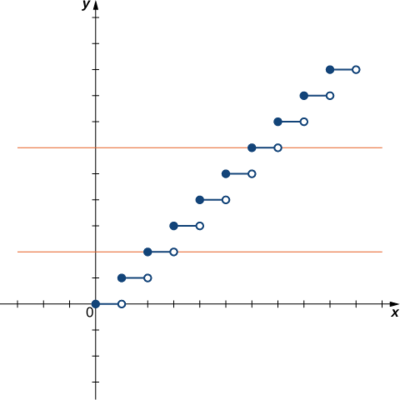
b) Como cada linha horizontal cruza o gráfico uma vez (no máximo), essa função é individual.

Exercício\(\PageIndex{1}\)

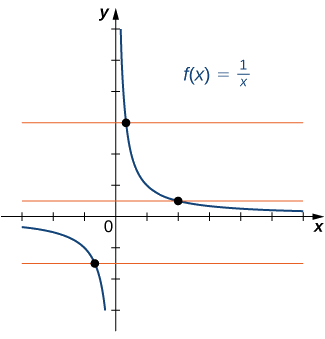
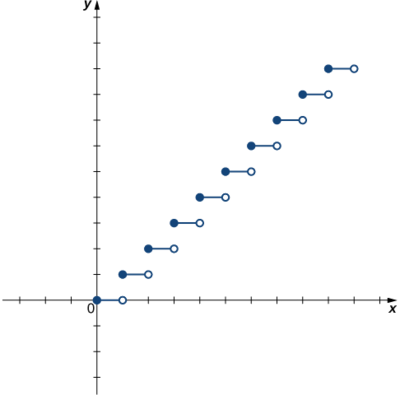
A função está\(f\) representada graficamente na imagem a seguir, individualmente?

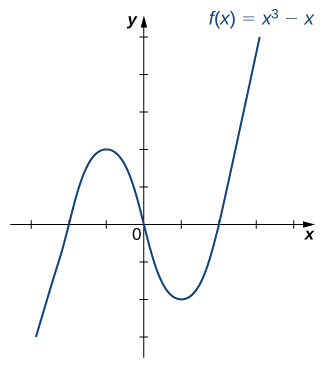
Solução

Use o teste de linha horizontal.

Responda

Não

Encontrando o inverso de uma função

Agora podemos considerar funções individuais e mostrar como encontrar suas inversas. Lembre-se de que uma função mapeia elementos no domínio de\(f\) até elementos no intervalo de\(f\). A função inversa mapeia cada elemento do intervalo de\(f\) volta até o elemento correspondente do domínio de\(f\). Portanto, para encontrar a função inversa de uma função um-para-um\(f\), dada qualquer uma\(y\) na faixa de\(f\), precisamos determinar qual\(x\) no domínio de\(f\) satisfaz\(f(x)=y\). Como\(f\) é individual, existe exatamente um desses valores\(x\). Podemos encontrar esse valor\(x\) resolvendo a equação\(f(x)=y\) para\(x\). Fazendo isso, podemos escrever\(x\) como uma função de\(y\) onde o domínio dessa função é o intervalo de\(f\) e o alcance dessa nova função é o domínio de\(f\). Consequentemente, essa função é o inverso de\(f\), e nós escrevemos\(x=f^{−1}(y)\). Como normalmente usamos a variável\(x\) para denotar a variável independente e y para denotar a variável dependente, geralmente trocamos as funções de\(x\) e e\(y\) e escrevemos\(y=f^{−1}(x)\). Representar a função inversa dessa maneira também é útil posteriormente, quando representamos graficamente uma função\(f\) e seu inverso\(f^{−1}\) nos mesmos eixos.

Estratégia de resolução de problemas: encontrando uma função inversa

1. Resolva a equação\(y=f(x)\) para\(x\).
2. Troque as variáveis\(x\)\(y\) e escreva\(y=f^{−1}(x)\).

Exemplo\(\PageIndex{2}\): Finding an Inverse Function

Encontre o inverso para a função\(f(x)=3x−4.\) State o domínio e o alcance da função inversa. Verifique se\(f^{−1}(f(x))=x.\)

Solução

Siga as etapas descritas na estratégia.

Etapa 1. Se\(y=3x−4,\) então\(3x=y+4\) e\(x=\frac{1}{3}y+\frac{4}{3}.\)

Etapa 2. Reescreva como\(y=\frac{1}{3}x+\frac{4}{3}\) e deixe\(y=f^{−1}(x)\) .Portanto,\(f^{−1}(x)=\frac{1}{3}x+\frac{4}{3}\).

Como o domínio de\(f\) é\((−∞,∞)\), o intervalo de\(f^{−1}\) é\((−∞,∞)\). Como o intervalo de\(f\) é\((−∞,∞)\), o domínio de\(f^{−1}\) é\((−∞,∞)\).

Você pode verificar isso\(f^{−1}(f(x))=x\) escrevendo

\(f^{−1}(f(x))=f^{−1}(3x−4)=\frac{1}{3}(3x−4)+\frac{4}{3}=x−\frac{4}{3}+\frac{4}{3}=x.\)

Observe que for\(f^{−1}(x)\) é o inverso de\(f(x)\), ambos\(f^{−1}(f(x))=x\) e\(f(f^{−1}(x))=x\) para todos\(x\) no domínio da função interna.

Exercício\(\PageIndex{2}\)

Encontre o inverso da função\(f(x)=3x/(x−2)\). Indique o domínio e o alcance da função inversa.

Dica

Use a estratégia de resolução de problemas para encontrar funções inversas.

Responda

\(f^{−1}(x)=\dfrac{2x}{x−3}\). O domínio de\(f^{−1}\) é\(\{x\,|\,x≠3\}\). O alcance de\(f^{−1}\) é\(\{y\,|\,y≠2\}\).

Representação gráfica de funções inversas

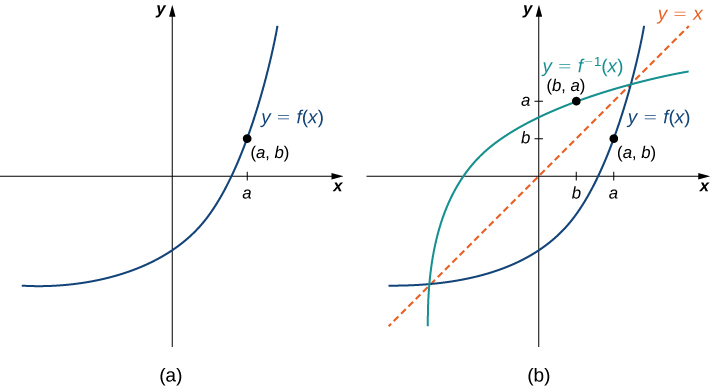
Vamos considerar a relação entre o gráfico de uma função\(f\) e o gráfico de seu inverso. Considere o gráfico\(f\) mostrado na Figura\(\PageIndex{3}\) e um ponto\((a,b)\) no gráfico. Desde\(b=f(a)\) então\(f^{−1}(b)=a\). Portanto, quando representamos graficamente\(f^{−1}\), o ponto\((b,a)\) está no gráfico. Como resultado, o gráfico de\(f^{−1}\) é um reflexo do gráfico de\(f\) cerca da linha\(y=x\).

Figura\(\PageIndex{3}\): (a) O gráfico desta função\(f\) mostra o ponto\((a,b)\) no gráfico de\(f\). (b) Como\((a,b)\) está no gráfico de\(f\), o ponto\((b,a)\) está no gráfico de\(f^{−1}\). O gráfico de\(f^{−1}\) é um reflexo do gráfico de\(f\) cerca da linha\(y=x\).

Exemplo\(\PageIndex{3}\): Sketching Graphs of Inverse Functions

Para o gráfico de\(f\) na imagem a seguir, esboce um gráfico de\(f^{−1}\) desenhando a linha\(y=x\) e usando simetria. Identifique o domínio e a faixa de\(f^{−1}\).

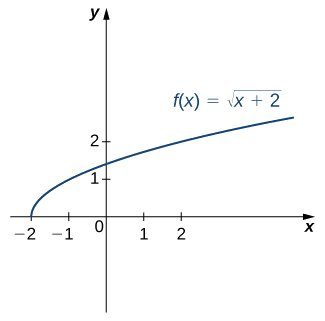
Solução

Reflita o gráfico sobre a linha\(y=x\). O domínio de\(f^{−1}\) é\([0,∞)\). O alcance de\(f^{−1}\) é\([−2,∞)\). Usando a estratégia anterior para encontrar funções inversas, podemos verificar se a função inversa é\(f^{−1}(x)=x^2−2\), conforme mostrado no gráfico.

Exercício\(\PageIndex{3}\)

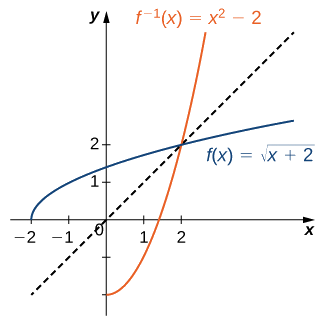
Esboce o gráfico\(f(x)=2x+3\) e o gráfico de seu inverso usando a propriedade de simetria das funções inversas.

Dica

Os gráficos são simétricos em relação à linha\(y=x\)

Responda

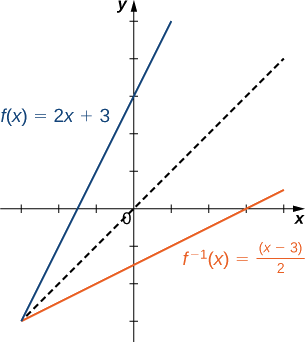
Restringindo domínios

Como vimos,\(f(x)=x^2\) não tem uma função inversa porque não é um para um. No entanto, podemos escolher um subconjunto do domínio de\(f\) tal forma que a função seja individual. Esse subconjunto é chamado de domínio restrito. Ao restringir o domínio de\(f\), podemos definir uma nova função de\(g\) forma que o domínio de\(g\) seja o domínio restrito de\(f\) e\(g(x)=f(x)\) para todos\(x\) no domínio de\(g\). Então, podemos definir uma função inversa para\(g\) nesse domínio. Por exemplo, como\(f(x)=x^2\) é um para um no intervalo\([0,∞)\), podemos definir uma nova função\(g\) tal que o domínio de\(g\) é\([0,∞)\) e\(g(x)=x^2\) para todos\(x\) em seu domínio. Como\(g\) é uma função individual, ela tem uma função inversa, dada pela fórmula\(g^{−1}(x)=\sqrt{x}\). Por outro lado, a função também\(f(x)=x^2\) é individual no domínio\((−∞,0]\). Portanto, também poderíamos definir uma nova função\(h\) tal que o domínio de\(h\) é\((−∞,0]\) e\(h(x)=x^2\) para todos\(x\) no domínio de\(h\). Então\(h\) é uma função um-para-um e também deve ter um inverso. Seu inverso é dado pela fórmula\(h^{−1}(x)=−\sqrt{x}\) (Figura\(\PageIndex{4}\)).

Figura\(\PageIndex{4}\): (a) Para\(g(x)=x^2\) restringido a\([0,∞)\),\(g^{−1}(x)=\sqrt{x}\). (b) Para\(h(x)=x^2\) restringido a\((−∞,0]\),\(h^{−1}(x)=−\sqrt{x}\).

Exemplo\(\PageIndex{4}\): Restricting the Domain

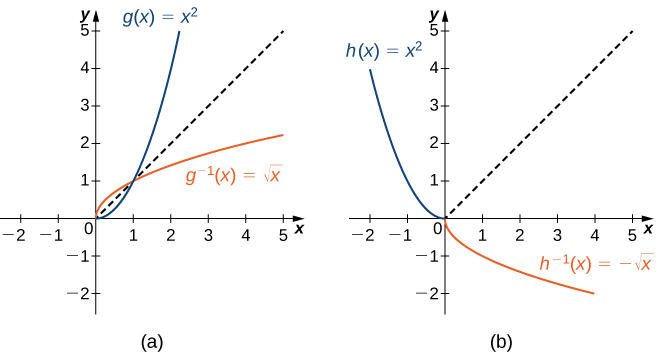
Considere a função\(f(x)=(x+1)^2\).

1. Esboce o gráfico\(f\) e use o teste de linha horizontal para mostrar que não\(f\) é individual.
2. Mostre que\(f\) é individual no domínio restrito\([−1,∞)\). Determine o domínio e o intervalo para o inverso de\(f\) neste domínio restrito e encontre uma fórmula para\(f^{−1}\).

Solução

a) O gráfico de\(f\) é o gráfico da\(1\) unidade esquerda\(y=x^2\) deslocada. Como existe uma linha horizontal cruzando o gráfico mais de uma vez, não\(f\) é um para um.

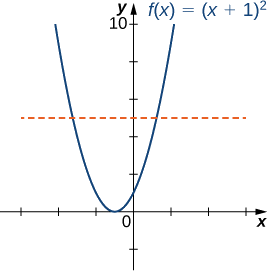
b) No intervalo\([−1,∞),\;f\) é um para um.

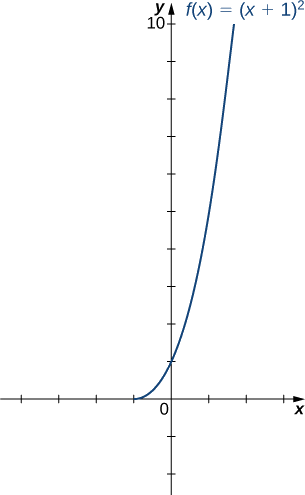
O domínio e o intervalo de\(f^{−1}\) são dados pelo intervalo e domínio de\(f\), respectivamente. Portanto, o domínio de\(f^{−1}\) é\([0,∞)\) e o intervalo de\(f^{−1}\) é\([−1,∞)\). Para encontrar uma fórmula para\(f^{−1}\), resolva a equação\(y=(x+1)^2\) para\(x.\) If\(y=(x+1)^2\), então\(x=−1±\sqrt{y}\). Como estamos restringindo o domínio ao intervalo em\(x≥−1\) que precisamos\(±\sqrt{y}≥0\). Portanto,\(x=−1+\sqrt{y}\). Intercambiando\(x\) e\(y\), escrevemos\(y=−1+\sqrt{x}\) e concluímos isso\(f^{−1}(x)=−1+\sqrt{x}\).

Exercício\(\PageIndex{4}\)

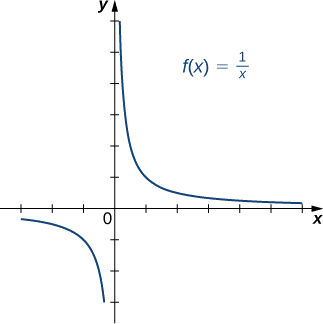
Considere\(f(x)=1/x^2\) restrito ao domínio\((−∞,0)\). Verifique se\(f\) é individual neste domínio. Determine o domínio e o intervalo do inverso de\(f\) e encontre uma fórmula para\(f^{−1}\).

Dica

O domínio e o intervalo de\(f^{−1}\) são dados pelo intervalo e domínio de\(f\), respectivamente. Para encontrar\(f^{−1}\), resolva\(y=1/x^2\)\(x\).

Responda

O domínio de\(f^{−1}\) é\((0,∞)\). O alcance de\(f^{−1}\) é\((−∞,0)\). A função inversa é dada pela fórmula\(f^{−1}(x)=−1/\sqrt{x}\).

Funções trigonométricas inversas

As seis funções trigonométricas básicas são periódicas e, portanto, não são individuais. No entanto, se restringirmos o domínio de uma função trigonométrica a um intervalo em que ela seja um para um, podemos definir seu inverso. Considere a função seno. A função seno é individual em um número infinito de intervalos, mas a convenção padrão é restringir o domínio ao intervalo\(\left[−\frac{π}{2},\frac{π}{2}\right]\). Ao fazer isso, definimos a função seno inverso no domínio de\([−1,1]\) forma que, para qualquer um\(x\) no intervalo\([−1,1]\), a função seno inverso nos informe qual ângulo\(θ\) no intervalo é\(\left[−\frac{π}{2},\frac{π}{2}\right]\) satisfatório\(\sin θ=x\). Da mesma forma, podemos restringir os domínios das outras funções trigonométricas para definir funções trigonométricas inversas, que são funções que nos dizem qual ângulo em um determinado intervalo tem um valor trigonométrico especificado.

Definição: funções trigonométricas inversas

A função de seno inverso, denotada\(\sin^{−1}\) ou\(\arcsin\), e a função de cosseno inverso, denotada\(\cos^{−1}\) ou\(\arccos\), são definidas no domínio da\(D=\{x|−1≤x≤1\}\) seguinte forma:

\(\sin^{−1}(x)=y\)

• se e somente se\(\sin(y)=x\) e\(−\frac{π}{2}≤y≤\frac{π}{2}\);

\(\cos^{−1}(x)=y\)

• se e somente se\(\cos(y)=x\)\(0≤y≤π\) e.

A função tangente inversa, denotada\(\tan^{−1}\) ou\(\arctan\), e a função cotangente inversa, denotada\(\cot^{−1}\) ou\(\operatorname{arccot}\), são definidas no domínio da\(D=\{x|−∞<x<∞\}\) seguinte forma:

\(\tan^{−1}(x)=y\)

• se e somente se\(\tan(y)=x\) e\(−\frac{π}{2}<y<\frac{π}{2}\);

\(\cot^{−1}(x)=y\)

• se e somente se\(\cot(y)=x\)\(0<y<π\) e.

A função cossecante inversa, denotada\(\csc^{−1}\) ou\(\operatorname{arccsc}\), e a função secante inversa, denotada\(\sec^{−1}\) ou\(\operatorname{arcsec}\), são definidas no domínio da\(D=\{x\,|\,|x|≥1\}\) seguinte forma:

\(\csc^{−1}(x)=y\)

• se e somente se\(\csc(y)=x\) e\(−\frac{π}{2}≤y≤\frac{π}{2}, \, y≠0\);

\(\sec^{−1}(x)=y\)

• se e somente se\(\sec(y)=x\)\(0≤y≤π, \, y≠π/2\) e.

Para representar graficamente as funções trigonométricas inversas, usamos os gráficos das funções trigonométricas restritas aos domínios definidos anteriormente e refletimos os gráficos sobre a linha\(y=x\) (Figura\(\PageIndex{5}\)).

Figura\(\PageIndex{5}\): O gráfico de cada uma das funções trigonométricas inversas é uma reflexão sobre a linha\(y=x\) da função trigonométrica restrita correspondente.

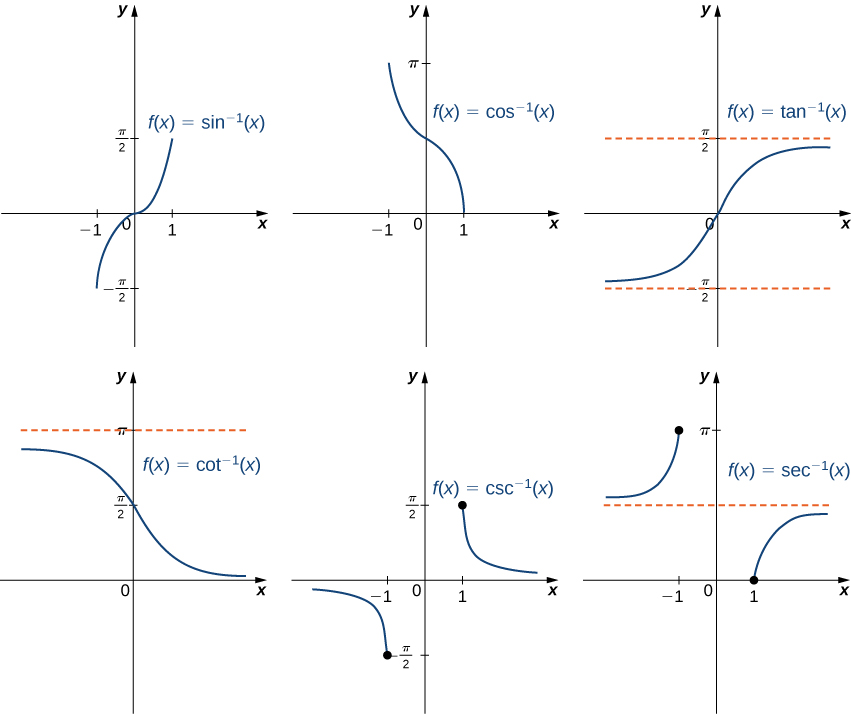
Ao avaliar uma função trigonométrica inversa, a saída é um ângulo. Por exemplo, para avaliar\(\cos^{−1}\left(\frac{1}{2}\right)\), precisamos encontrar um ângulo\(θ\) como esse\(\cos θ=\frac{1}{2}\). Claramente, muitos ângulos têm essa propriedade. No entanto, dada a definição de\(\cos^{−1}\), precisamos do ângulo\(θ\) que não apenas resolva essa equação, mas também esteja no intervalo\([0,π]\). Concluímos isso\(\cos^{−1}\left(\frac{1}{2}\right)=\frac{π}{3}\).

Agora consideramos a composição de uma função trigonométrica e seu inverso. Por exemplo, considere as duas expressões\(\sin\left(\sin^{−1}\left(\frac{\sqrt{2}}{2}\right)\right)\) e\(\sin^{−1}(\sin(π)).\)

Para o primeiro, simplificamos da seguinte forma:

\[\sin\left(\sin^{−1}\left(\frac{\sqrt{2}}{2}\right)\right)=\sin\left(\frac{π}{4}\right)=\frac{\sqrt{2}}{2}.\nonumber \]

Para o segundo, temos

\[\sin^{−1}(\sin(π))=\sin^{−1}(0)=0.\nonumber \]

A função inversa deve “desfazer” a função original, então por que\(\sin^{−1}(\sin(π))=π?\) relembrar nossa definição de funções inversas, uma função\(f\) e seu inverso não\(f^{−1}\) satisfazem as condições\(f(f^{−1}(y))=y\) para todos\(y\) no domínio de\(f^{−1}\) e\(f^{−1}(f(x))=x\) para todos\(x\) em o domínio de\(f\), então o que aconteceu aqui? O problema é que a função senoidal inversa\(\sin^{−1}\),, é a inversa da função senoidal restrita definida no domínio\(\left[−\frac{π}{2},\frac{π}{2}\right]\). Portanto, pois\(x\) no intervalo\([−\frac{π}{2},\frac{π}{2}]\), é verdade que\(\sin^{−1}(\sin x)=x\). No entanto, para valores\(x\) fora desse intervalo, a equação não é válida, mesmo que\(\sin^{−1}(\sin x)\) esteja definida para todos os números reais\(x\).

E quanto\(\sin(\sin^{−1}y)?\) a Isso tem um problema semelhante? A resposta é não. Como o domínio de\(\sin^{−1}\) é o intervalo\([−1,1]\), concluímos que\(\sin\left(\sin^{−1}y\right)=y\) if\(−1≤y≤1\) e a expressão não estão definidos para outros valores de\(y\). Para resumir,

\(\sin(\sin^{−1}y)=y\)E se\(−1≤y≤1\)

e

\(\sin^{−1}(\sin x)=x\)E se\(−\frac{π}{2}≤x≤\frac{π}{2}.\)

Da mesma forma, para a função cosseno,

\(\cos(\cos^{−1}y)=y\)E se\(−1≤y≤1\)

e

\(\cos^{−1}(\cos x)=x\)E se\(0≤x≤π.\)

Propriedades semelhantes valem para as outras funções trigonométricas e seus inversos.

Exemplo\(\PageIndex{5}\): Evaluating Expressions Involving Inverse Trigonometric Functions

Avalie cada uma das expressões a seguir.

1. \(\sin^{−1}\left(−\frac{\sqrt{3}}{2}\right)\)
2. \(\tan\left(\tan^{−1}\left(−\frac{1}{\sqrt{3}}\right)\right)\)
3. \(\cos^{−1}\left(\cos\left(\frac{5π}{4}\right)\right)\)
4. \(\sin^{−1}\left(\cos\left(\frac{2π}{3}\right)\right)\)

Solução

1. Avaliar\(\sin^{−1}(−\sqrt{3}/2)\) é equivalente a encontrar o ângulo de\(θ\) tal forma que\(\sin θ=−\sqrt{3}/2\)\(−π/2≤θ≤π/2\) e. O ângulo\(θ=−π/3\) satisfaz essas duas condições. Portanto,\(\sin^{−1}(−\sqrt{3}/2)=−π/3\).
2. Primeiro, usamos o fato de que\(\tan^{−1}(−1/\sqrt{3})=−π/6.\) Então\(\tan(-π/6)=−1/\sqrt{3}\). Portanto,\(\tan(\tan^{−1}(−1/\sqrt{3}))=−1/\sqrt{3}\).
3. Para avaliar\(\cos^{−1}(\cos(5π/4))\), primeiro use o fato de que\(\cos(5π/4)=−\sqrt{2}/2\). Então precisamos encontrar o ângulo de\(θ\) tal forma que\(\cos(θ)=−\sqrt{2}/2\)\(0≤θ≤π\) e. Uma vez que\(3π/4\) satisfaz essas duas condições, nós temos\(\cos^{-1}(\cos(5π/4))=\cos^{−1}(−\sqrt{2}/2))=3π/4\).
4. Desde então\(\cos(2π/3)=−1/2\), precisamos avaliar\(\sin^{−1}(−1/2)\). Ou seja, precisamos encontrar o ângulo de\(θ\) tal forma que\(\sin(θ)=−1/2\)\(−π/2≤θ≤π/2\) e. Como\(−π/6\) satisfaz essas duas condições, podemos concluir que\(\sin^{−1}(\cos(2π/3))=\sin^{−1}(−1/2)=−π/6.\)

O valor máximo de uma função

Em muitas áreas da ciência, engenharia e matemática, é útil saber o valor máximo que uma função pode obter, mesmo que não saibamos seu valor exato em um determinado instante. Por exemplo, se tivermos uma função descrevendo a resistência de uma viga de teto, gostaríamos de saber o peso máximo que a viga pode suportar sem quebrar. Se tivermos uma função que descreva a velocidade de um trem, gostaríamos de saber sua velocidade máxima antes que ele pule dos trilhos. O design seguro geralmente depende do conhecimento dos valores máximos.

Este projeto descreve um exemplo simples de uma função com um valor máximo que depende de dois coeficientes de equação. Veremos que os valores máximos podem depender de vários fatores além da variável independente\(x\).

1. Considere o gráfico na Figura\(\PageIndex{6}\) da função\(y=\sin x+\cos x.\) Descreva sua forma geral. É periódico? Como você sabe?

Figura\(\PageIndex{6}\): O gráfico de\(y=\sin x+\cos x\).

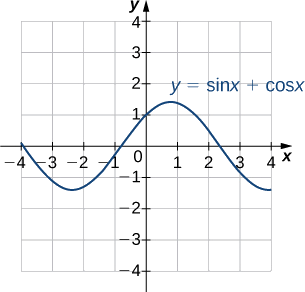
Usando uma calculadora gráfica ou outro dispositivo gráfico, estime os\(y\) valores\(x\) - e -do ponto máximo para o gráfico (o primeiro desses pontos onde\(x > 0\)). Pode ser útil expressar o\(x\) valor -como um múltiplo de\(π.\)

2. Agora, considere outros gráficos do formulário\(y=A\sin x+B\cos x\) para vários valores de\(A\) e\(B.\) desenhe o gráfico quando\(A = 2\)\(B = 1,\) e encontre os\(y\) valores\(x\) - e -para o ponto máximo. (Lembre-se de expressar o\(x\) valor -como um múltiplo de\(π\), se possível.) Ele se moveu?

3. Repita para\(A = 1, \,B = 2.\) Existe alguma relação com o que você encontrou na parte (2)?

4. Complete a tabela a seguir, adicionando algumas opções próprias para\(A\) e\(B:\)

\(A\)	\(B\)	\(x\)	\(y\)	\(A\)	\(B\)	\(x\)	\(y\)
\ (A\)” style="vertical-align:middle; ">0	\ (B\)” style="alinhamento vertical: médio; ">1	\ (x\)” style="alinhamento vertical: meio; ">	\ (y\)” style="vertical-align:middle; ">	\ (A\)” style="vertical-align:middle; ">3	\ (B\)” style="alinhamento vertical: médio; ">4	\ (x\)” style="alinhamento vertical: meio; ">	\ (y\)” style="vertical-align:middle; ">
\ (A\)” style="vertical-align:middle; ">1	\ (B\)” style="alinhamento vertical: médio; ">0	\ (x\)” style="alinhamento vertical: meio; ">	\ (y\)” style="vertical-align:middle; ">	\ (A\)” style="vertical-align:middle; ">4	\ (B\)” style="alinhamento vertical: médio; ">3	\ (x\)” style="alinhamento vertical: meio; ">	\ (y\)” style="vertical-align:middle; ">
\ (A\)” style="vertical-align:middle; ">1	\ (B\)” style="alinhamento vertical: médio; ">1	\ (x\)” style="alinhamento vertical: meio; ">	\ (y\)” style="vertical-align:middle; ">	\ (A\)” style="vertical-align:middle; ">\(\sqrt{3}\)	\ (B\)” style="alinhamento vertical: médio; ">1	\ (x\)” style="alinhamento vertical: meio; ">	\ (y\)” style="vertical-align:middle; ">
\ (A\)” style="vertical-align:middle; ">1	\ (B\)” style="alinhamento vertical: médio; ">2	\ (x\)” style="alinhamento vertical: meio; ">	\ (y\)” style="vertical-align:middle; ">	\ (A\)” style="vertical-align:middle; ">1	\ (B\)” style="alinhamento vertical: médio; ">\(\sqrt{3}\)	\ (x\)” style="alinhamento vertical: meio; ">	\ (y\)” style="vertical-align:middle; ">
\ (A\)” style="vertical-align:middle; ">2	\ (B\)” style="alinhamento vertical: médio; ">1	\ (x\)” style="alinhamento vertical: meio; ">	\ (y\)” style="vertical-align:middle; ">	\ (A\)” style="vertical-align:middle; ">12	\ (B\)” style="alinhamento vertical: médio; ">5	\ (x\)” style="alinhamento vertical: meio; ">	\ (y\)” style="vertical-align:middle; ">
\ (A\)” style="vertical-align:middle; ">2	\ (B\)” style="alinhamento vertical: médio; ">2	\ (x\)” style="alinhamento vertical: meio; ">	\ (y\)” style="vertical-align:middle; ">	\ (A\)” style="vertical-align:middle; ">5	\ (B\)” style="alinhamento vertical: médio; ">12	\ (x\)” style="alinhamento vertical: meio; ">	\ (y\)” style="vertical-align:middle; ">

5. Tente descobrir a fórmula para os\(y\) valores -.

6. A fórmula para os\(x\) valores -é um pouco mais difícil. Os pontos mais úteis da tabela são\((1,1),\, (1,\sqrt{3}),\, (\sqrt{3},1).\) (Dica: considere funções trigonométricas inversas).

7. Se você encontrou fórmulas para as peças (5) e (6), mostre que elas funcionam juntas. Ou seja, substitua a fórmula\(x\) -value que você encontrou\(y=A\sin x+B\cos x\) e simplifique-a para chegar à fórmula de\(y\) -valor que você encontrou.

Conceitos-chave

• Para que uma função tenha um inverso, a função deve ser um para um. Dado o gráfico de uma função, podemos determinar se a função é individual usando o teste de linha horizontal.
• Se uma função não for individual, podemos restringir o domínio a um domínio menor, onde a função é individual, e então definir o inverso da função no domínio menor.
• Para uma função\(f\) e seu inverso\(f^{−1},\, f(f^{−1}(x))=x\) para todos\(x\) no domínio de\(f^{−1}\) e\(f^{−1}(f(x))=x\) para todos\(x\) no domínio de\(f\).
• Como as funções trigonométricas são periódicas, precisamos restringir seus domínios para definir as funções trigonométricas inversas.
• O gráfico de uma função\(f\) e seu inverso\(f^{−1}\) são simétricos em relação à linha\(y=x.\)

Equações-chave

• Função inversa

\(f^{−1}(f(x))=x\)para todos\(x\)\(D,\) e\(f(f^{−1}(y))=y\) para todos\(y\) em\(R\).

Glossário

teste de linha horizontal

uma função\(f\) é individual se e somente se cada linha horizontal cruzar o gráfico de\(f\), no máximo, uma vez

função inversa

para uma função\(f\), a função inversa\(f^{−1}\) satisfaz\(f^{−1}(y)=x\) se\(f(x)=y\)

funções trigonométricas inversas

os inversos das funções trigonométricas são definidos em domínios restritos, onde são funções individuais

função um para um

uma função\(f\) é um para um se\(f(x_1)≠f(x_2)\) se\(x_1≠x_2\)

domínio restrito

um subconjunto do domínio de uma função\(f\)