1.2E: Exercícios para a Seção 1.2

Last updated
Save as PDF

Page ID: 188619

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Nos exercícios 1 a 8, para cada par de pontos,

a. encontre a inclinação da linha que passa pelos pontos e

b. indica se a linha está aumentando, diminuindo, horizontal ou vertical.

1)$(-2,4)$ e$(1,1)$

Resposta: a.$m = −1$
b. Diminuindo

2)$(-1,4)$ e$(3,-1)$

3)$(3,5)$ e$(-1,2)$

Resposta: a.$m = 3/4$
b. Aumentando

4)$(6,4)$ e$(4,-3)$

5)$(2,3)$ e$(5,7)$

Resposta: a.$m = 4/3$
b. Aumentando

6)$(1,9)$ e$(-8,5)$

7)$(2,4)$ e$(1,4)$

Resposta: a.$m = 0$
b. Horizontal

8)$(1,4)$ e$(1,0)$

Nos exercícios 9 a 16, escreva a equação da reta que satisfaz as condições dadas na forma de interceptação de inclinação.

9) Inclinação =$−6$, passa por$(1,3)$

Resposta: $y=−6x+9$

10) Inclinação =$3$, passa por$(-3,2)$

11) Inclinação =$\frac{1}{3}$, passa por$(0,4)$

Resposta: $y=\frac{1}{3}x+4$

12) Inclinação =$\frac{2}{5}$,$x$ -intercepto =$8$

13) Passando por$(2,1)$ e$(−2,−1)$

Resposta: $y=\frac{1}{2}x$

14) Passando por$(−3,7)$ e$(1,2)$

15)$x$ -intercept =$5$ e$y$ -intercept =$−3$

Resposta: $y=\frac{3}{5}x−3$

16)$x$ -Intercept =−$6$ e$y$ -intercept =$9$

Nos exercícios 17 a 24, para cada equação linear,

a. forneça a inclinação$m$ e$y$ -intercepte,$b,$ se houver, e

b. represente graficamente a linha.

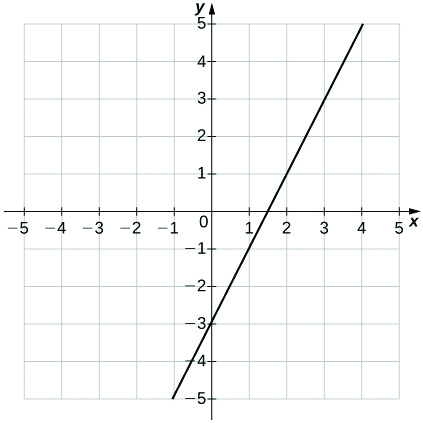
17)$y=2x−3$

Resposta

uma.$m=2,\;b=−3$

$Uma imagem de um gráfico. O eixo x vai de -5 a 5 e o eixo y vai de -5 a 5. O gráfico mostra uma função crescente de linha reta com um intercepto y em (0, -3) e um intercepto x em (1,5, 0).$

18)$y=−\frac{1}{7}x+1$

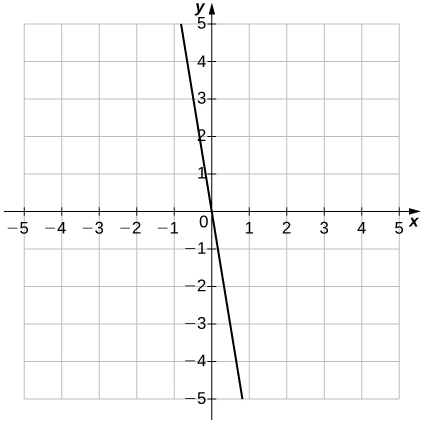
19)$f(x)=-6x$

Resposta

uma.$m=−6,\; b=0$

$Uma imagem de um gráfico. O eixo x vai de -5 a 5 e o eixo y vai de -5 a 5. O gráfico mostra uma função de linha reta decrescente com um intercepto y e um intercepto x, ambos na origem. Há um ponto sem rótulo na função em (0,5, -3).$

20)$f(x)=−5x+4$

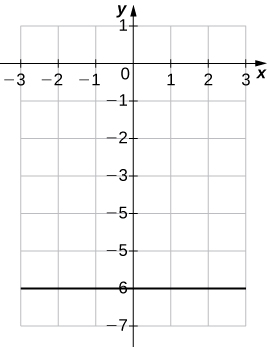
21)$4y+24=0$

Resposta

uma.$ m=0,\;b=−6$

$Uma imagem de um gráfico. O eixo x vai de -3 a 3 e o eixo y vai de -7 a 1. O gráfico mostra uma função de linha reta horizontal com um intercepto y em (0, -6) e sem interceptação x.$

22)$8x-4=0$

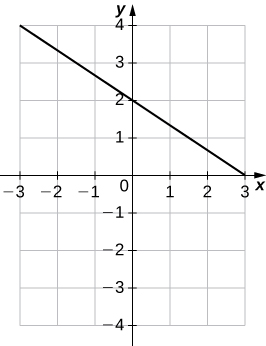
23)$2x+3y=6$

Resposta

uma.$m=−\frac{2}{3},\; b=2$

$Uma imagem de um gráfico. O eixo x vai de -3 a 3 e o eixo y vai de -4 a 4. O gráfico mostra uma função de linha reta decrescente com um intercepto y em (0, 2) e um intercepto x em (3, 0).$

24)$6x−5y+15=0$

Nos exercícios 25 a 29, para cada polinômio,

a. encontre o diploma;

b. encontre os zeros, se houver;

c. encontre o (s)$y$ intercepto (s) -, se houver;

d. use o coeficiente principal para determinar o comportamento final do gráfico; e

e. determine algebricamente se o polinômio é par, ímpar ou nenhum dos dois.

25)$f(x)=2x^2−3x−5$

Resposta: a.$2$
b.$\frac{5}{2},\;−1$;
c.$−5$
d. Ambas as extremidades se elevam
e. Nenhuma

26)$f(x)=−3x^2+6x$

27)$f(x)=\frac{1}{2}x^2−1$

Resposta: a.$2$
b. ±$\sqrt{2}$
c.$−1$
d. Ambas as extremidades se elevam
e. Par

28)$f(x)=x^3+3x^2−x−3$

29)$f(x)=3x−x^3$

Resposta: a.$3$
b.$0,$ ±$\sqrt{3}$
c.$0$
d. A extremidade esquerda sobe, a extremidade direita cai
e. Ímpar

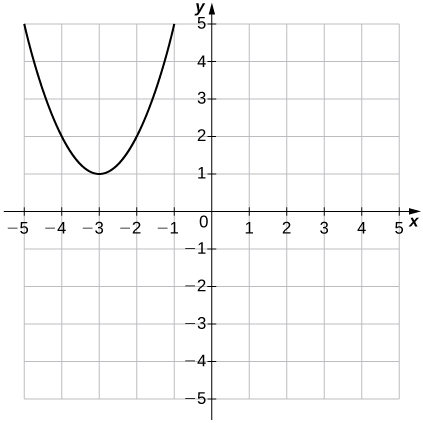
Para os exercícios 30 a 31, use o gráfico de$f(x)=x^2$ para representar graficamente cada função transformada$g$.

30)$g(x)=x^2−1$

31)$g(x)=(x+3)^2+1$

Resposta: $Uma imagem de um gráfico. O eixo x vai de -5 a 5 e o eixo y vai de -5 a 5. O gráfico mostra uma função parabólica que diminui até o ponto (-3, 1) e depois começa a aumentar. O intercepto y não é mostrado e não há interceptações x. Há dois pontos não representados graficamente em (-4, 2) e (-2, 2).$

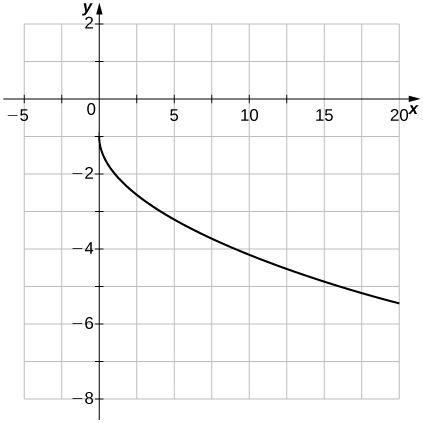
Para os exercícios 32 a 33, use o gráfico de$f(x)=\sqrt{x}$ para representar graficamente cada função transformada$g$.

32)$g(x)=\sqrt{x+2}$

33)$g(x)=−\sqrt{x}−1$

Resposta: $Uma imagem de um gráfico. O eixo x vai de -5 a 20 e o eixo y vai de -8 a 2. O gráfico mostra uma função curva que começa no ponto (0, -1) e depois começa a diminuir. O intercepto y está em (0, -1) e não há interceptação x. Há um ponto não plotado em (9, -4).$

Para os exercícios 34 a 35, use o gráfico de$y=f(x)$ para representar graficamente cada função transformada$g$.

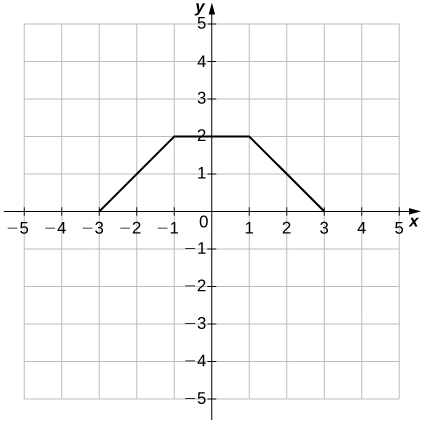
$Uma imagem de um gráfico. O eixo x vai de -5 a 5 e o eixo y vai de -5 a 5. O gráfico mostra uma função que começa no ponto (-3, 0), onde começa a aumentar até o ponto (-1, 2). Depois do ponto (-1, 2), a função se torna uma linha horizontal e permanece assim até o ponto (1, 2). Depois do ponto (1, 2), a função começa a diminuir até o ponto (3, 0), onde a função termina.$

34)$g(x)=f(x)+1$

(35)$g(x)=f(x−1)+2$

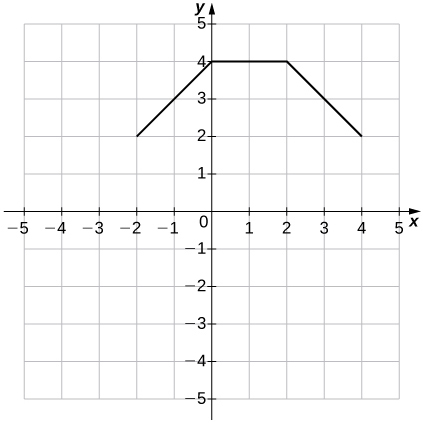
Resposta: $Uma imagem de um gráfico. O eixo x vai de -5 a 5 e o eixo y vai de -5 a 5. O gráfico mostra uma função que começa no ponto (-2, 2), onde começa a aumentar até o ponto (0, 4). Depois do ponto (0, 4), a função se torna uma linha horizontal e permanece assim até o ponto (2, 4). Depois do ponto (2, 4), a função começa a diminuir até o ponto (4, 2), onde a função termina.$

Nos exercícios 36 a 39, para cada uma das funções definidas por partes,

a. avaliar com os valores dados da variável independente, e

b. esboce o gráfico.

36)$f(x)=\begin{cases}4x+3, & &\text{if } x≤0\\ -x+1, & &\text{if } x>0\end{cases} ;\quad f(−3);\; f(0);\; f(2)$

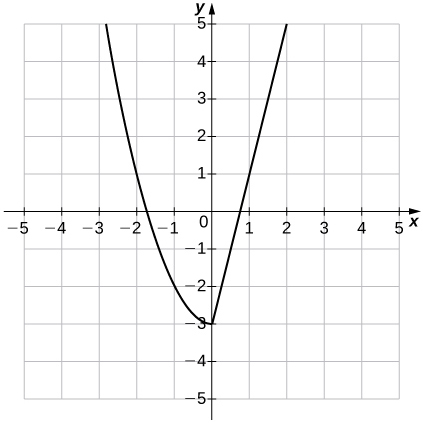
37)$f(x)=\begin{cases}x^2-3, & &\text{if } x≤0\\ 4x-3, & &\text{if } x>0\end{cases} ;\quad f(−4);\; f(0);\; f(2)$

Resposta

uma.$f(−4) = 13,\quad f(0)=−3,\quad f(2)=5$

$Uma imagem de um gráfico. O eixo x vai de -5 a 5 e o eixo y vai de -5 a 5. O gráfico é de uma função que tem duas partes. A primeira peça é uma curva decrescente que termina no ponto (0, -3). A segunda peça é uma linha crescente que começa no ponto (0, -3). A função tem uma interceptação x no ponto aproximado (1,7, 0) e no ponto (0,75, 0) e uma interceptação y em (0, -3).$

38)$h(x)=\begin{cases}x+1, & &\text{if }x≤5\\4, & &\text{if } x>5\end{cases} ;\quad h(0);\; h(π);\; h(5)$

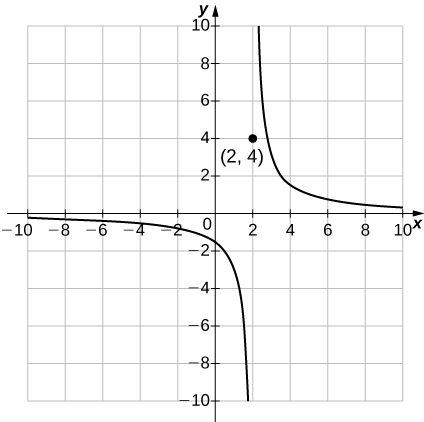
39)$g(x)=\begin{cases}\dfrac{3}{x−2}, & &\text{if }x≠2\\4, & &\text{if } x=2\end{cases} ;\quad g(0);\; g(−4);\; g(2)$

Resposta

uma.$g(0) = -\frac{3}{2},\; g(-4)=-\frac{1}{2},\; g(2)=4$

$Uma imagem de um gráfico. O eixo x vai de -10 a 10 e o eixo y vai de -10 a 10. O gráfico é de uma função que começa um pouco abaixo do eixo x e começa a diminuir. À medida que a função se aproxima da linha vertical não traçada de “x = 2”, ela diminui a uma taxa mais rápida, mas nunca atinge a linha “x = 2”. No lado direito da linha não traçada “x = 2”, a função começa na parte superior do gráfico e começa a diminuir e se aproxima da linha horizontal não traçada “y = 0”, mas nunca alcança “y = 0”. A função também inclui um ponto representado graficamente em (2, 4). Há um intercepto y em (0, -1,5) e nenhum intercepto x.$

Nos exercícios 40 a 44, determine se a afirmação é verdadeira ou falsa. Explique o porquê.

40)$f(x)=\dfrac{4x+1}{7x−2}$ é uma função transcendental.

41)$g(x)=\sqrt[3]{x}$ é uma função raiz ímpar.

Resposta: É verdade;$n=3$

42) Uma função logarítmica é uma função algébrica.

43) Uma função da forma$f(x)=x^b$, onde$b$ é uma constante de valor real, é uma função exponencial.

Resposta: Falso;$f(x)=x^b$, onde$b$ é uma constante de valor real, é uma função de potência

44) O domínio de uma função de raiz par são todos números reais.

45) [T] Uma empresa compra alguns equipamentos de informática por $20.500. Ao final de um período de 3 anos, o valor do equipamento diminuiu linearmente para $12.301.

a. Encontre uma função$y=V(t)$ que determine o valor$V$ do equipamento no final dos$t$ anos.

b. Encontre e interprete o significado das$y$ interceptações$x$ - e -para essa situação.

c. Qual é o valor do equipamento ao final de 5 anos?

d. Quando o valor do equipamento será de $3000?

Resposta: a.$V(t)=−2733t+20500$
b.$(0,20,500)$ significa que o preço inicial de compra do equipamento é de $20.500;$(7.5,0)$ significa que em$7.5$ anos o equipamento de informática não tem valor.
c. $6835
d. Em aproximadamente$6.4$ anos

46) [T] O total de compras on-line durante as férias de Natal aumentou dramaticamente nos últimos 5 anos. Em 2012$(t=0)$, as vendas totais de fim de ano on-line foram de $42,3 bilhões, enquanto em 2013 foram de $48,1 bilhões.

a. Encontre uma função linear$S$ que estime o total de vendas de feriados on-line no ano$t.$

b. Interprete a inclinação do gráfico de$S.$

c. Use a parte a. para prever o ano em que as compras on-line durante o Natal chegarão a 60 bilhões de dólares.

47) [T] Uma padaria familiar faz cupcakes e os vende em festivais locais ao ar livre. Para um festival de música, há um custo fixo de $125 para montar uma barraca de cupcakes. O proprietário estima que custa $0,75 para fazer cada cupcake. O proprietário está interessado em determinar o custo$C$ total em função do número de cupcakes feitos.

a. Encontre uma função linear que relacione o custo$C$ com$x,$ o número de cupcakes feitos.

b. Encontre o custo para assar$160$ cupcakes.

c. Se a dona vender os cupcakes por $1,50 cada, quantos cupcakes ela precisa vender para começar a lucrar? (Dica: use a função INTERSECTION em uma calculadora para encontrar esse número.)

Resposta: a.$C=0.75x+125$
b. $245
c.$167$ cupcakes

48) [T] Espera-se que uma casa comprada por $250.000 valha o dobro do preço de compra em 18 anos.

a. Encontre uma função linear que modela o preço$P$ da casa versus o número de anos$t$ desde a compra original.

b. Interprete a inclinação do gráfico de$P.$

c. Encontre o preço da casa$15$ anos a partir de quando ela foi originalmente comprada.

49) [T] Um carro foi comprado por $26.000. O valor do carro se deprecia em $1500 por ano.

a. Encontre uma função linear que modela o valor$V$ do carro após$t$ anos.

b. Encontre e interprete$V(4)$.

Resposta: a.$V(t)=−1500t+26,000$
b. Em$4$ anos, o valor do carro é de $20.000.

50) [T] Um condomínio em uma parte nobre da cidade foi comprado por $432.000. Em$35$ anos, vale $60.500. Encontre a taxa de depreciação.

51) [T] O custo total$C$ (em milhares de dólares) para produzir um determinado item é modelado pela função$C(x)=10.50x+28,500$, onde$x$ está o número de itens produzidos. Determine o custo de produção$175$ dos itens.

Resposta: $30.337.500

52) [T] Uma professora pede que sua turma relate a quantidade de tempo$t$ que passou escrevendo duas tarefas. A maioria dos alunos relata que demoram cerca de$45$ minutos para digitar uma tarefa de quatro páginas e cerca de$1.5$ horas para digitar uma tarefa de nove páginas.

a. Encontre a função linear$y=N(t)$ que modela essa situação, onde$N$ é o número de páginas digitadas e$t$ o tempo em minutos.

b. Use a parte a. para determinar quantas páginas podem ser digitadas em$2$ horas.

c. Use a parte a. para determinar quanto tempo leva para digitar uma tarefa de 20 páginas.

53) [T] A produção (como porcentagem da capacidade total) das usinas nucleares nos Estados Unidos pode ser modelada pela função$P(t)=1.8576t+68.052$, onde$t$ é o tempo em anos e$t=0$ corresponde ao início de 2000. Use o modelo para prever a produção percentual em 2015.

Resposta: 96% da capacidade total

54) [T] O escritório de admissões de uma universidade pública estima que 65% dos estudantes admitidos na turma de 2019 realmente se matricularão.

a. Encontre a função linear$y=N(x)$, onde$N$ está o número de alunos que realmente se matriculam e$x$ é o número de todos os alunos que foram admitidos na turma de 2019.

b. Se a universidade quiser que o tamanho da turma de calouros de 2019 seja 1350, determine quantos alunos devem ser admitidos.

Colaboradores

Template:ContribOpenStaxCalc