1.2: Classes básicas de funções

Last updated
Save as PDF

Page ID: 188601

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de

Calcule a inclinação de uma função linear e interprete seu significado.
Reconheça o grau de um polinômio.
Encontre as raízes de um polinômio quadrático.
Descreva os gráficos das funções polinomiais pares e ímpares básicas.
Identifique uma função racional.
Descreva os gráficos das funções de potência e raiz.
Explique a diferença entre funções algébricas e transcendentais.
Faça um gráfico de uma função definida por partes.
Esboce o gráfico de uma função que foi deslocada, esticada ou refletida a partir da posição inicial do gráfico.

Estudamos as características gerais das funções, então agora vamos examinar algumas classes específicas de funções. Começamos revisando as propriedades básicas das funções lineares e quadráticas e, em seguida, generalizamos para incluir polinômios de maior grau. Ao combinar funções raiz com polinômios, podemos definir funções algébricas gerais e distingui-las das funções transcendentais que examinamos posteriormente neste capítulo. Concluímos a seção com exemplos de funções definidas por partes e examinamos como esboçar o gráfico de uma função que foi deslocada, esticada ou refletida a partir de sua forma inicial.

Funções lineares e inclinação

O tipo de função mais fácil de considerar é uma função linear. As funções lineares têm a forma$f(x)=ax+b$, onde$a$ e$b$ são constantes. Na Figura$\PageIndex{1}$, vemos exemplos de funções lineares quando a é positivo, negativo e zero. Observe que$a>0$, se, o gráfico da linha aumenta à medida que$x$ aumenta. Em outras palavras,$f(x)=ax+b$ está aumentando$(−∞, ∞)$. Se$a<0$, o gráfico da linha cai à medida que$x$ aumenta. Nesse caso,$f(x)=ax+b$ está diminuindo em$(−∞, ∞)$. Se$a=0$ sim, a linha é horizontal.

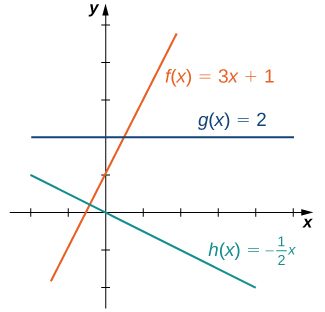
Uma imagem de um gráfico. O eixo y vai de -2 a 5 e o eixo x vai de -2 a 5. O gráfico é das 3 funções. A primeira função é “f (x) = 3x + 1”, que é uma linha reta crescente com um intercepto x em (-1/3), 0) e um intercepto y em (0, 1). A segunda função é “g (x) = 2”, que é uma linha horizontal com um intercepto y em (0, 2) e sem interceptação x. A terceira função é “h (x) = (-1/2) x”, que é uma linha reta decrescente com um intercepto x e um intercepto y ambos na origem. A função f (x) está aumentando a uma taxa maior do que a função h (x) está diminuindo. — Figura$\PageIndex{1}$: Essas funções lineares estão aumentando ou diminuindo$(∞, ∞)$ e uma função é uma linha horizontal.

Conforme sugerido pela Figura$\PageIndex{1}$, o gráfico de qualquer função linear é uma linha. Uma das características distintivas de uma linha é sua inclinação. A inclinação é a mudança$y$ para cada mudança de unidade em$x$. A inclinação mede a inclinação e a direção de uma linha. Se a inclinação for positiva, a linha aponta para cima ao se mover da esquerda para a direita. Se a inclinação for negativa, a linha aponta para baixo ao se mover da esquerda para a direita. Se a inclinação for zero, a linha será horizontal. Para calcular a inclinação de uma linha, precisamos determinar a razão entre a mudança em$y$ e a mudança em$x$. Para fazer isso, escolhemos quaisquer dois pontos$(x_1,y_1)$ e$(x_2,y_2)$ na linha e calculamos$\dfrac{y_2−y_1}{x_2−x_1}$. Na Figura$\PageIndex{2}$, vemos que essa proporção é independente dos pontos escolhidos.

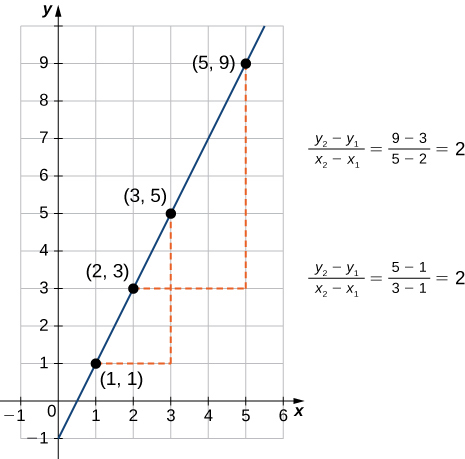
Uma imagem de um gráfico. O eixo y vai de -1 a 10 e o eixo x vai de -1 a 6. O gráfico é de uma função que é uma linha reta crescente. Há quatro pontos rotulados na função em (1, 1), (2, 3), (3, 5) e (5, 9). Há uma linha horizontal pontilhada do ponto de função rotulado (1, 1) até o ponto sem rótulo (3, 1) que não está na função e, em seguida, uma linha vertical pontilhada do ponto sem rótulo (3, 1), que não está na função, até o ponto de função rotulado (3, 5). Esses dois pontos têm o rótulo “(y2 - y1)/(x2 - x1) = (5 -1)/(3 - 1) = 2”. Há uma linha horizontal pontilhada do ponto de função rotulado (2, 3) até o ponto sem rótulo (5, 3) que não está na função e, em seguida, uma linha vertical pontilhada do ponto sem rótulo (5, 3), que não está na função, até o ponto de função rotulado (5, 9). Esses dois pontos têm o rótulo “(y2 - y1)/(x2 - x1) = (9 -3)/(5 - 2) = 2”. — Figura$\PageIndex{2}$: Para qualquer função linear, a inclinação$(y_2−y_1)/(x_2−x_1)$ é independente da escolha dos pontos$(x_1,y_1)$ e$(x_2,y_2)$ da linha.

Definição: Inclinação de uma função linear

Considere a linha$L$ passando por pontos$(x_1,y_1)$$(x_2,y_2)$ e. Deixe$Δy=y_2−y_1$ e$Δx=x_2−x_1$ denote as mudanças em$y$ e$x$, respectivamente. A inclinação da linha é

\[m=\dfrac{y_2−y_1}{x_2−x_1}=\dfrac{Δy}{Δx} \nonumber \]

Agora examinamos a relação entre a inclinação e a fórmula para uma função linear. Considere a função linear dada pela fórmula$f(x)=ax+b$. Conforme discutido anteriormente, sabemos que o gráfico de uma função linear é dado por uma linha. Podemos usar nossa definição de inclinação para calcular a inclinação dessa linha. Conforme mostrado, podemos determinar a inclinação$(y_2−y_1)/(x_2−x_1)$ calculando quaisquer pontos$(x_1,y_1)$ e$(x_2,y_2)$ na linha. Avaliando a função$f$ em$x=0$, vemos que$(0,b)$ é um ponto nessa linha. Avaliando essa função em$x=1$, vemos que também$(1,a+b)$ é um ponto nessa linha. Portanto, a inclinação dessa linha é

\[\dfrac{(a+b)−b}{1−0}=a. \nonumber \]

Mostramos que o coeficiente$a$ é a inclinação da linha. Podemos concluir que a fórmula$f(x)=ax+b$ descreve uma linha com inclinação$a$. Além disso, como essa linha cruza o$y$ eixo -no ponto$(0,b)$, vemos que o$y$ intercepto -para essa função linear é$(0,b)$. Concluímos que a fórmula nos$f(x)=ax+b$ diz a inclinação$a$,, e o$y$ intercepto$(0,b)$ -, para essa linha. Como costumamos usar o símbolo$m$ para indicar a inclinação de uma linha, podemos escrever

\[\underbrace{f(x)=mx+b}_{\text{slope-intercept form}} \nonumber \]

para denotar a forma de interceptação de inclinação de uma função linear.

Às vezes, é conveniente expressar uma função linear de maneiras diferentes. Por exemplo, suponha que o gráfico de uma função linear passe pelo ponto$(x_1,y_1)$ e a inclinação da linha seja$m$. Uma vez que qualquer outro ponto$(x,f(x))$ no gráfico de$f$ deve satisfazer a equação

\[m=\dfrac{f(x)−y_1}{x−x_1}, \nonumber \]

esta função linear pode ser expressa escrevendo

\[\underbrace{f(x)−y_1=m(x−x_1)}_{\text{point-slope equation}}. \nonumber \]

Chamamos essa equação de equação de ponto de inclinação para essa função linear.

Como toda linha não vertical é o gráfico de uma função linear, os pontos em uma linha não vertical podem ser descritos usando as equações de interceptação de inclinação ou de inclinação de ponto. No entanto, uma linha vertical não representa o gráfico de uma função e não pode ser expressa em nenhuma dessas formas. Em vez disso, uma linha vertical é descrita pela equação$x=k$ para alguma constante$k$. Como nem a forma de interceptação de inclinação nem a forma de inclinação de ponto permitem linhas verticais, usamos a notação

\[\underbrace{ax+by=c}_{\text{standard form}}, \nonumber \]

onde ambos não$a,b$ são zero, para denotar a forma padrão de uma linha.

Definição: Equação de Ponto-Inclinação e Forma de Intercepção de Inclinação e Forma Padrão da Equação de uma Reta

Considere uma linha passando pelo ponto$(x_1,y_1)$ com inclinação$m$. A equação

\[y−y_1=m(x−x_1) \nonumber \]

é a equação de inclinação pontual para essa linha.

Considere uma linha com inclinação$m$ e$y$ -intercepte$(0,b).$ A equação

\[y=mx+b \nonumber \]

é uma equação para essa linha na forma de interceptação de inclinação.

A forma padrão de uma linha é dada pela equação

\[ax+by=c, \nonumber \]

onde$a$ e ambos não$b$ são zero. Esse formulário é mais geral porque permite uma linha vertical,$x=k$.

Exemplo$\PageIndex{1}$: Finding the Slope and Equations of Lines

Considere a linha que passa pelos pontos$(11,−4)$ e$(−4,5)$, conforme mostrado na Figura$\PageIndex{3}$.

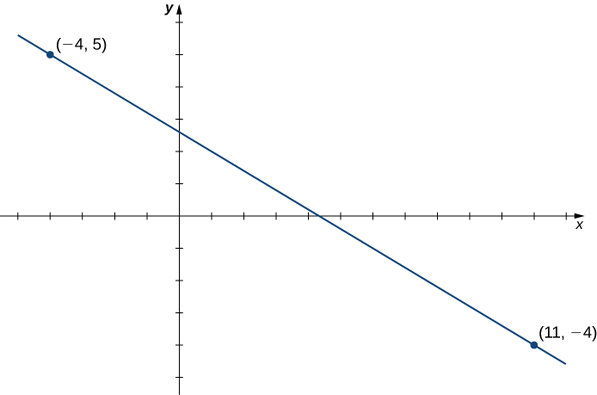
Uma imagem de um gráfico. O eixo x vai de -5 a 12 e o eixo y vai de -5 a 6. O gráfico é da função que é uma linha reta decrescente. A função tem dois pontos traçados, em (-4, 5) e (11, 4). — Figura$\PageIndex{3}$: Encontrando a equação de uma função linear com um gráfico que é uma linha entre dois pontos dados.

Encontre a inclinação da linha.
Encontre uma equação para essa função linear na forma de inclinação de pontos.
Encontre uma equação para essa função linear na forma de interceptação de inclinação.

Solução

1. A inclinação da linha é

\[m=\dfrac{y_2−y_1}{x_2−x_1}=\dfrac{5−(−4)}{−4−11}=−\dfrac{9}{15}=−\dfrac{3}{5}. \nonumber \]

2. Para encontrar uma equação para a função linear na forma de inclinação de pontos, use a inclinação$m=−3/5$ e escolha qualquer ponto na linha. Se escolhermos o ponto$(11,−4)$, obtemos a equação

\[f(x)+4=−\dfrac{3}{5}(x−11). \nonumber \]

3. Para encontrar uma equação para a função linear na forma de interceptação de inclinação, resolva a equação na parte b. para$f(x)$. Quando fazemos isso, obtemos a equação

\[f(x)=−\dfrac{3}{5}x+\dfrac{13}{5}. \nonumber \]

Exercício$\PageIndex{1}$

Considere a linha passando por pontos$(−3,2)$$(1,4)$ e.

Encontre a inclinação da linha.
Encontre uma equação dessa reta na forma de inclinação de pontos.
Encontre uma equação dessa reta na forma de interceptação de inclinação.

Dica: A inclinação$m=Δy/Δx$.

Responda a: $m=1/2$.
Resposta b: A forma de inclinação do ponto é$y−4=\dfrac{1}{2}(x−1)$.
Resposta c: A forma de interceptação de inclinação é$y=\dfrac{1}{2}x+\dfrac{7}{2}$.

Exemplo$\PageIndex{2}$:

Jessica sai de casa às 5:50 da manhã e sai para uma corrida de 9 milhas. Ela volta para sua casa às 7h08. Responda às seguintes perguntas, supondo que Jessica corra em um ritmo constante.

Descreva a distância$D$ (em milhas) que Jessica percorre como uma função linear de seu tempo de execução$t$ (em minutos).
Esboce um gráfico de$D$.
Interprete o significado da inclinação.

Solução

a. Às vezes$t=0$, Jessica está na casa dela, então$D(0)=0$. Em$t=78$ alguns minutos, Jessica terminou de correr$9$ mi, então$D(78)=9$. A inclinação da função linear é

\[m=\dfrac{9−0}{78−0}=\dfrac{3}{26}.\nonumber \]

O$y$ intercepto -é$(0,0)$, então a equação para essa função linear é

\[D(t)=\dfrac{3}{26}t. \nonumber \]

b. Para representar graficamente$D$, use o fato de que o gráfico passa pela origem e tem inclinação$m=3/26.$

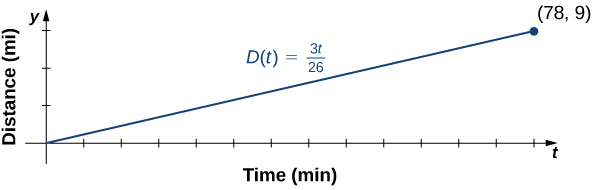
$Uma imagem de um gráfico. O eixo y é rotulado como “y, distância em milhas”. O eixo x é rotulado como “t, tempo em minutos”. O gráfico é da função “D (t) = 3t/26”, que é uma linha reta crescente que começa na origem. A função termina no ponto traçado (78, 9).$

c. A inclinação$m=3/26≈0.115$ descreve a distância (em milhas) que Jessica corre por minuto, ou sua velocidade média.

Polinômios

Uma função linear é um tipo especial de uma classe mais geral de funções: polinômios. Uma função polinomial é qualquer função que possa ser escrita na forma

\[f(x)=a_nx^n+a_{n−1}x^{n−1}+…+a_1x+a_0 \nonumber \]

para alguns números inteiros$n≥0$ e constantes$a_n,a_{n−1},…,a_0$, onde$a_n≠0$. No caso em que$n=0$, permitimos por$a_0=0$; if$a_0=0$, a função$f(x)=0$ é chamada de função zero. O valor$n$ é chamado de grau do polinômio; a constante$a_n$ é chamada de coeficiente principal. Uma função linear da forma$f(x)=mx+b$ é um polinômio de grau 1 if$m≠0$ e grau 0 if$m=0$. Um polinômio de grau 0 também é chamado de função constante. Uma função polinomial de grau 2 é chamada de função quadrática. Em particular, uma função quadrática tem a forma

\[f(x)=ax^2+bx+c, \nonumber \]

onde$a≠0$. Uma função polinomial de grau$3$ é chamada de função cúbica.

Funções de potência

Algumas funções polinomiais são funções de potência. Uma função de potência é qualquer função da forma$f(x)=ax^b$, onde$a$ e$b$ estão quaisquer números reais. O expoente em uma função de potência pode ser qualquer número real, mas aqui consideramos o caso quando o expoente é um número inteiro positivo. (Consideraremos outros casos posteriormente.) Se o expoente for um inteiro positivo, então$f(x)=ax^n$ é um polinômio. Se$n$ for par, então$f(x)=ax^n$ é uma função par porque$f(−x)=a(−x)^n=ax^n$$n$ é par. Se$n$ é ímpar, então$f(x)=ax^n$ é uma função ímpar porque$f(−x)=a(−x)^n=−ax^n$$n$ é ímpar (Figura$\PageIndex{4}$).

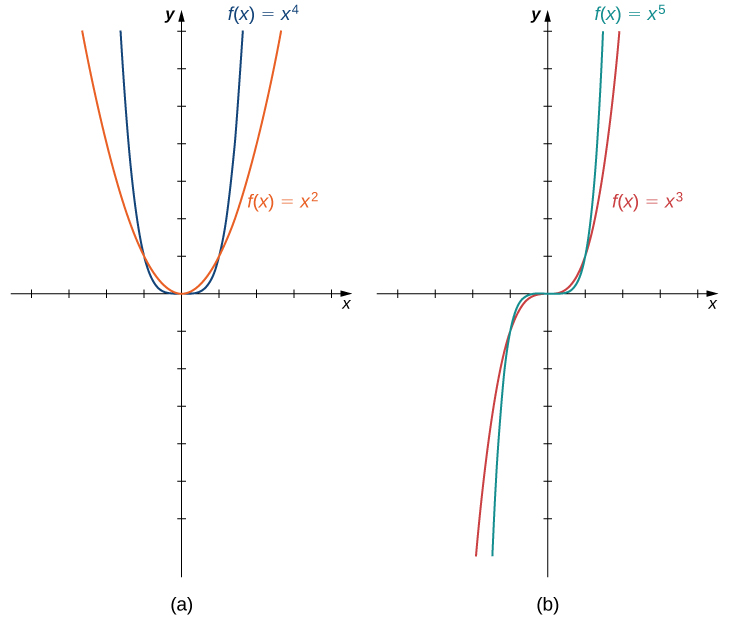
Uma imagem de dois gráficos. Ambos os gráficos têm um eixo x que vai de -4 a 4 e um eixo y que vai de -6 a 7. O primeiro gráfico é rotulado como “a” e tem duas funções. A primeira função é “f (x) = x to the 4th”, que é uma parábola que diminui até a origem e depois aumenta novamente após a origem. A segunda função é “f (x) = x ao quadrado”, que é uma parábola que diminui até a origem e depois aumenta novamente após a origem, mas aumenta e diminui a uma taxa mais lenta do que a primeira função. O segundo gráfico é rotulado como “b” e tem duas funções. A primeira função é “f (x) = x to the 5th”, que é uma função curva que aumenta até a origem, se torna uniforme na origem e depois aumenta novamente após a origem. A segunda função é “f (x) = x ao cubo”, que é uma função curva que aumenta até a origem, se torna uniforme na origem e depois aumenta novamente após a origem, mas aumenta a uma taxa mais lenta do que a primeira função. — Figura$\PageIndex{4}$: (a) Para qualquer número inteiro par$n$,$f(x)=ax^n$ é uma função par. (b) Para qualquer número inteiro ímpar$n$,$f(x)=ax^n$ é uma função ímpar.

Comportamento no infinito

Para determinar o comportamento de uma função à$f$ medida que as entradas se aproximam do infinito, observamos os valores à$f(x)$ medida que as entradas se tornam maiores.$x$ Para algumas funções, os valores de$f(x)$ se aproximam de um número finito. Por exemplo, para a função$f(x)=2+1/x$, os valores$1/x$ ficam cada vez mais próximos de zero para todos os valores à$x$ medida que ficam cada vez maiores. Para essa função, dizemos “$f(x)$se aproxima de dois quando$x$ vai para o infinito” e escrevemos$f(x)→2$ como$x→∞$. A linha$y=2$ é uma assíntota horizontal para a função$f(x)=2+1/x$ porque o gráfico da função se aproxima da linha à$x$ medida que aumenta.

Para outras funções, os valores$f(x)$ podem não se aproximar de um número finito, mas podem se tornar maiores para todos os valores$x$ à medida que aumentam. Nesse caso, dizemos “$f(x)$se aproxima do infinito como$x$ se aproxima do infinito” e escrevemos$f(x)→∞$ como$x→∞$. Por exemplo, para a função$f(x)=3x^2$, as saídas$f(x)$ ficam maiores à medida que as entradas$x$ aumentam. Podemos concluir que a função$f(x)=3x^2$ se aproxima do infinito à medida que$x$ se aproxima do infinito, e escrevemos$3x^2→∞$ como$x→∞$. O comportamento como$x→−∞$ e o significado de$f(x)→−∞$ como$x→∞$ ou$x→−∞$ podem ser definidos de forma semelhante. Podemos descrever o que acontece com os valores de as$x→∞$ e$f(x)$$x→−∞$ como o comportamento final da função.

Para entender o comportamento final das funções polinomiais, podemos nos concentrar nas funções quadráticas e cúbicas. O comportamento de polinômios de maior grau pode ser analisado de forma semelhante. Considere uma função quadrática$f(x)=ax^2+bx+c$. Se$a>0$, os valores são$f(x)→∞$$x→±∞$. Se$a<0$, os valores são$f(x)→−∞$$x→±∞$. Como o gráfico de uma função quadrática é uma parábola, a parábola se abre para cima se$a>0$.; a parábola se abre para baixo se$a<0$ (Figura$\PageIndex{5a}$).

Agora, considere uma função cúbica$f(x)=ax^3+bx^2+cx+d$. Se$a>0$, então$f(x)→∞$ como$x→∞$ e$f(x)→−∞$ como$x→−∞$. Se$a<0$, então$f(x)→−∞$ como$x→∞$ e$f(x)→∞$ como$x→−∞$. Como podemos ver nesses dois gráficos, o termo principal do polinômio determina o comportamento final (Figura$\PageIndex{5b}$).

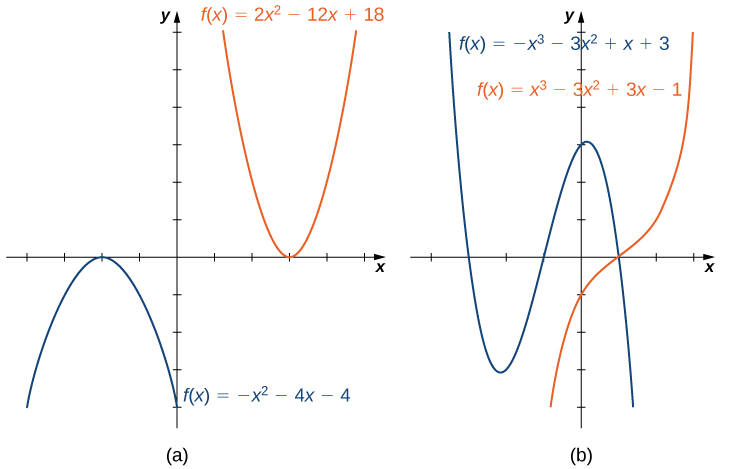
Uma imagem de dois gráficos. O primeiro gráfico é rotulado como “a” e tem um eixo x que vai de -4 a 5 e um eixo y que vai de -4 a 6. O gráfico contém duas funções. A primeira função é “f (x) = - (x ao quadrado) - 4x -4”, que é uma parábola. A função aumenta até atingir o máximo no ponto (-2, 0) e depois começa a diminuir. O intercepto x está em (-2, 0) e o intercepto y está em (0, -4). A segunda função é “f (x) = 2 (x ao quadrado) -12x + 16”, que é uma parábola. A função diminui até atingir o ponto mínimo em (3, -2) e então começa a aumentar. Os interceptos x estão em (2, 0) e (4, 0) e o intercepto y não é mostrado. O segundo gráfico é denominado “b” e tem um eixo x que vai de -4 a 3 e um eixo y que vai de -4 a 6. O gráfico contém duas funções. A primeira função é “f (x) = - (x ao cubo) - 3 (x ao quadrado) + x + 3”. O gráfico diminui até o ponto aproximado em (-2,2, -3,1), depois aumenta até o ponto aproximado em (0,2, 3,1) e começa a diminuir novamente. As interceptações x estão em (-3, 0), (-1, 0) e (1, 0). O intercepto y está em (0, 3). A segunda função é “f (x) = (x ao cubo) -3 (x ao quadrado) + 3x - 1”. É uma função curva que aumenta até o ponto (1, 0), onde se nivela. Após esse ponto, a função começa a aumentar novamente. Ele tem um intercepto x em (1, 0) e um intercepto y em (0, -1). — Figura$\PageIndex{5}$: (a) Para uma função quadrática, se o coeficiente principal$a>0$, a parábola se abre para cima. Se$a<0$, a parábola se abre para baixo. (b) Para uma função cúbica$f$, se o coeficiente principal$a>0$, os valores$f(x)→∞$ como$x→∞$ e os valores$f(x)→−∞$ como$x→−∞$. Se o coeficiente principal$a<0$, o oposto é verdadeiro.

Zeros de funções polinomiais

Outra característica do gráfico de uma função polinomial é onde ela cruza o$x$ eixo. Para determinar onde uma função$f$ cruza o$x$ eixo -, precisamos resolver a equação$f(x)=0$ para$x$. No caso da função linear$f(x)=mx+b$, o$x$ intercepto -é dado pela resolução da equação$mx+b=0$. Nesse caso, vemos que o$x$ intercepto -é dado por$(−b/m,0)$. No caso de uma função quadrática, encontrar o (s)$x$ intercepto (s) -requer encontrar os zeros de uma equação quadrática:$ax^2+bx+c=0$. Em alguns casos, é fácil fatorar o polinômio$ax^2+bx+c$ para encontrar os zeros. Caso contrário, usamos a fórmula quadrática.

A fórmula quadrática

Considere a equação quadrática

\[ax^2+bx+c=0, \nonumber \]

onde$a≠0$. As soluções dessa equação são dadas pela fórmula quadrática

\[x=\dfrac{−b±\sqrt{b^2−4ac}}{2a}. \label{quad} \]

Se o discriminante$b^2−4ac>0$, a Equação\ ref {quad} nos diz que existem dois números reais que satisfazem a equação quadrática. Se$b^2−4ac=0$, essa fórmula nos diz que há apenas uma solução e é um número real. Se$b^2−4ac<0$, nenhum número real satisfaz a equação quadrática.

No caso de polinômios de maior grau, pode ser mais complicado determinar onde o gráfico cruza o$x$ eixo. Em alguns casos, é possível encontrar os$x$ interceptos -fatorando o polinômio para encontrar seus zeros. Em outros casos, é impossível calcular os valores exatos dos$x$ interceptos. No entanto, como vemos mais adiante no texto, em casos como esse, podemos usar ferramentas analíticas para aproximar (em um grau muito alto) onde os$x$ interceptos estão localizados. Aqui nos concentramos nos gráficos de polinômios para os quais podemos calcular seus zeros explicitamente.

Exemplo$\PageIndex{3}$: Graphing Polynomial Functions

Para as seguintes funções,

$f(x)=−2x^2+4x−1$
$f(x)=x^3−3x^2−4x$

descreva o comportamento de$f(x)$ como$x→±∞$,
encontre todos os zeros de$f$, e
esboce um gráfico de$f$.

Solução

1. A função$f(x)=−2x^2+4x−1$ é uma função quadrática.

1. Porque$a=−2<0$, como$x→±∞,f(x)→−∞.$

2. Para encontrar os zeros de$f$, use a fórmula quadrática. Os zeros são

$x=\dfrac{−4±\sqrt{4^2−4(−2)(−1)}}{2(−2)}=\dfrac{−4±\sqrt{8}}{−4}=\dfrac{−4±2\sqrt{2}}{−4}=\dfrac{2±\sqrt{2}}{2}.$

3. Para esboçar o gráfico de$f$, use as informações de suas respostas anteriores e combine-as com o fato de que o gráfico é uma parábola que se abre para baixo.

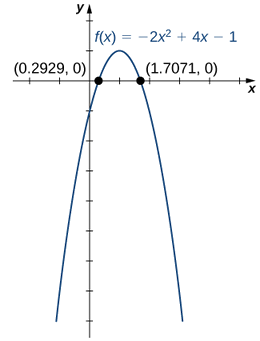
$Uma imagem de um gráfico. O eixo x vai de -2 a 5 e o eixo y vai de -8 a 2. O gráfico é da função “f (x) = -2 (x ao quadrado) + 4x - 1”, que é uma parábola. A função aumenta até o ponto máximo em (1, 1) e depois diminui. Ambos os pontos de interceptação x são plotados na função, em aproximadamente (0,2929, 0) e (1,7071, 0). O intercepto y está no ponto (0, -1).$

2. A função$f(x)=x^3−3x^2−4x$ é uma função cúbica.

1. Porque$a=1>0$, como$x→∞$,$f(x)→∞$. Como$x→−∞$,$f(x)→−∞$.

2. Para encontrar os zeros de$f$, precisamos fatorar o polinômio. Primeiro, quando$x$ consideramos todos os termos, encontramos

$f(x)=x(x^2−3x−4).$

Então, quando fatoramos a função quadrática$x^2−3x−4$, encontramos

$f(x)=x(x−4)(x+1).$

Portanto, os zeros de$f$ são$x=0,4,−1$.

3. Combinando os resultados das partes i. e ii., desenhe um esboço de$f$.

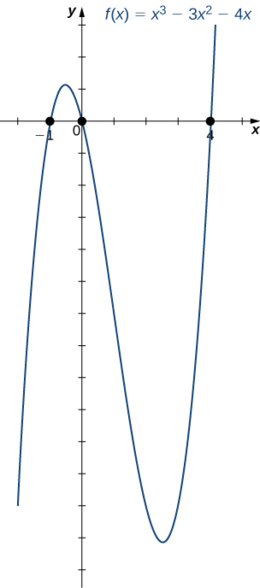
$Uma imagem de um gráfico. O eixo x vai de -2 a 5 e o eixo y vai de -14 a 7. O gráfico é da função curva “f (x) = (x ao cubo) - 3 (x ao quadrado) - 4x”. A função aumenta até o ponto aproximado em (-0,5, 1,1), depois diminui até o ponto aproximado (2,5, -13,1) e começa a aumentar novamente. Os pontos de interceptação x são plotados na função, em (-1, 0), (0, 0) e (4, 0). O intercepto y está na origem.$

Exercício$\PageIndex{2}$

Considere a função quadrática$f(x)=3x^2−6x+2.$ Encontre os zeros de$f$. A parábola se abre para cima ou para baixo?

Dica: Use a fórmula quadrática.

Responda: Os zeros são$x=1±\sqrt{3}/3$. A parábola se abre para cima.

Modelos matemáticos

Uma grande variedade de situações do mundo real pode ser descrita usando modelos matemáticos. Um modelo matemático é um método de simular situações da vida real com equações matemáticas. Físicos, engenheiros, economistas e outros pesquisadores desenvolvem modelos combinando observação com dados quantitativos para desenvolver equações, funções, gráficos e outras ferramentas matemáticas para descrever o comportamento de vários sistemas com precisão. Os modelos são úteis porque ajudam a prever resultados futuros. Exemplos de modelos matemáticos incluem o estudo da dinâmica populacional, investigações de padrões climáticos e previsões de vendas de produtos.

Como exemplo, vamos considerar um modelo matemático que uma empresa poderia usar para descrever sua receita com a venda de um item específico. A quantidade de receita que$R$ uma empresa recebe pela venda de$n$ itens vendidos a um preço de$p$ dólares por item é descrita pela equação$R=p⋅n$. A empresa está interessada em saber como as vendas mudam à medida que o preço do item muda. Suponha que os dados na Tabela$\PageIndex{1}$ mostrem o número de unidades que uma empresa vende em função do preço por item.

Tabela$\PageIndex{1}$: Número de unidades vendidas$n$ (em milhares) em função do preço por unidade$p$ (em dólares)
$p$	6	8	10	12	14
$n$	19,4	18,5	16.2	13,8	12.2

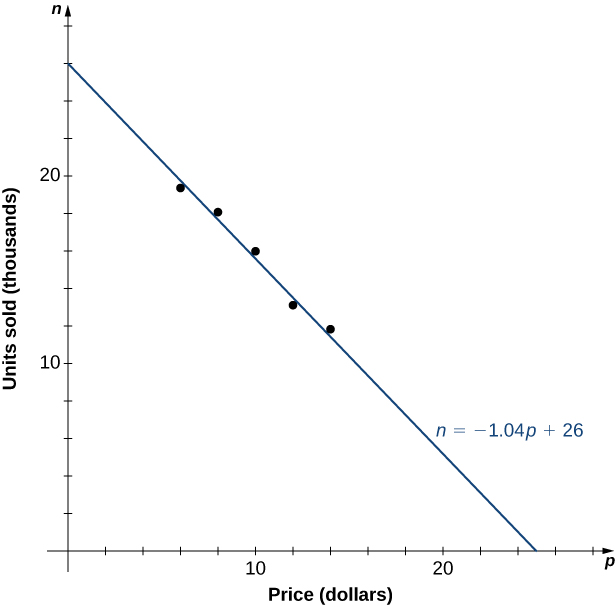
Na Figura$\PageIndex{6}$, vemos o gráfico do número de unidades vendidas (em milhares) em função do preço (em dólares). Observamos na forma do gráfico que o número de unidades vendidas é provavelmente uma função linear do preço por item, e os dados podem ser aproximados pela função$n= −1.04p+26$ linear de$0≤p≤25$, onde$n$ prevê o número de unidades vendidas em milhares. Usando essa função linear, a receita (em milhares de dólares) pode ser estimada pela função quadrática

\[R(p)=p⋅ (−1.04p+26)=−1.04p^2+26p \text{ for }0≤p≤25. \nonumber \]

No exemplo$\PageIndex{4}$, usamos essa função quadrática para prever a quantidade de receita que a empresa recebe, dependendo do preço que a empresa cobra por item. Observe que não podemos concluir definitivamente o número real de unidades vendidas por valores de$p$, para os quais nenhum dado é coletado. No entanto, dados os outros valores de dados e o gráfico mostrado, parece razoável que o número de unidades vendidas (em milhares) se o preço cobrado for$p$ dólares possa estar próximo dos valores previstos pela função linear$n=−1.04p+26.$

Uma imagem de um gráfico. O eixo y vai de 0 a 28 e é rotulado como “n, unidades vendidas em milhares”. O eixo x vai de 0 a 28 e é rotulado como “p, preço em dólares”. O gráfico é da função “n = -1,04p + 26”, que é uma função de linha decrescente que começa no ponto de interceptação y (0, 26). Há 5 pontos plotados no gráfico em (6, 19,4), (8, 18,5), (10, 16,2), (12, 13,8) e (14, 12,2). Os pontos não estão no gráfico da linha de função, mas estão muito próximos a ela. A função tem um intercepto x no ponto (25, 0). — Figura$\PageIndex{6}$: Os dados coletados para o número de itens vendidos em função do preço são aproximadamente lineares. Usamos a função linear$n=−1.04p+26$ para estimar essa função.

Exemplo$\PageIndex{4}$: Maximizing Revenue

Uma empresa está interessada em prever o valor da receita que receberá, dependendo do preço que cobra por um determinado item. Usando os dados da Tabela$\PageIndex{1}$, a empresa chega à seguinte função quadrática para modelar a receita$R$ em função do preço por item$p:$

\[R(p)=p⋅(−1.04p+26)=−1.04p^2+26p \nonumber \]

para$0≤p≤25$.

Preveja a receita se a empresa vender o item a um preço de$p=$5$$p=$17$ e.
Encontre os zeros dessa função e interprete o significado dos zeros.
Esboce um gráfico de$R$.
Use o gráfico para determinar o valor$p$ que maximiza a receita. Encontre a receita máxima.

Solução

a. Avaliando a função de receita em$p=5$ e$p=17$, podemos concluir que

$R(5)=−1.04(5)^2+26(5)=104,\text{ so revenue}=$104,000;$

$R(17)=−1.04(17)^2+26(17)=141.44,\text{ so revenue}=$141,440.$

b. Os zeros dessa função podem ser encontrados resolvendo a equação$−1.04p^2+26p=0$. Quando fatoramos a expressão quadrática, obtemos$p(−1.04p+26)=0$. As soluções para essa equação são dadas por$p=0,25$. Para esses valores de$p$, a receita é zero. Quando$p=$0$, a receita é zero porque a empresa está distribuindo suas mercadorias gratuitamente. Quando$p=$25$, a receita é zero porque o preço é muito alto e ninguém vai comprar nenhum item.

c. Sabendo que a função é quadrática, também sabemos que o gráfico é uma parábola. Como o coeficiente principal é negativo, a parábola se abre para baixo. Uma propriedade das parábolas é que elas são simétricas em relação ao eixo de simetria, então, como os zeros estão em$p=0$ e$p=25$, a parábola deve ser simétrica em relação à linha a meio caminho entre elas, ou$p=12.5$.

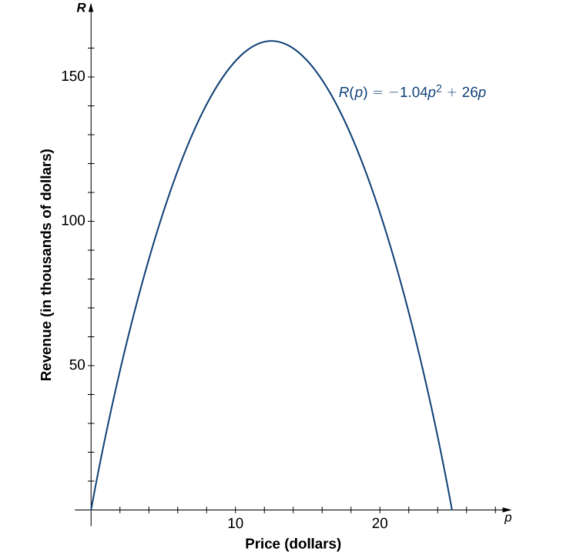
$Uma imagem de um gráfico. O eixo y vai de 0 a 170 e é rotulado como “R, receita em milhares de dólares”. O eixo x vai de 0 a 28 e é rotulado como “p, preço em dólares”. O gráfico é da função “n = -1,04 (p ao quadrado) + 26p”, que é uma parábola que começa na origem. A função aumenta até o ponto máximo em (12,5, 162,5) e então começa a diminuir. A função tem x interceptações na origem e no ponto (25, 0). O intercepto y está na origem.$

d. A função é uma parábola com zeros em$p=0$ e$p=25$, e é simétrica em relação à linha$p=12.5$, então a receita máxima ocorre a um preço de$p=$12.50$ por item. A esse preço, a receita é$R(p)=−1.04(12.5)^2+26(12.5)=$162,500.$

Funções algébricas

Ao permitir quocientes e potências fracionárias em funções polinomiais, criamos uma classe maior de funções. Uma função algébrica é aquela que envolve adição, subtração, multiplicação, divisão, poderes racionais e raízes. Dois tipos de funções algébricas são funções racionais e funções raiz.

Assim como números racionais são quocientes de números inteiros, funções racionais são quocientes de polinômios. Em particular, uma função racional é qualquer função da forma$f(x)=p(x)/q(x)$, onde$p(x)$ e$q(x)$ são polinômios. Por exemplo,

$f(x)=\dfrac{3x−1}{5x+2}$e$g(x)=\dfrac{4}{x^2+1}$

são funções racionais. Uma função raiz é uma função de potência da forma$f(x)=x^{1/n}$, onde$n$ é um número inteiro positivo maior que um. Por exemplo,$f(x)=x^{1/2}=\sqrt{x}$ é a função de raiz quadrada e$g(x)=x^{1/3}=\sqrt[3]{x}$ é a função de raiz cúbica. Ao permitir composições de funções raiz e funções racionais, podemos criar outras funções algébricas. Por exemplo,$f(x)=\sqrt{4−x^2}$ é uma função algébrica.

Exemplo$\PageIndex{5}$: Finding Domain and Range for Algebraic Functions

Para cada uma das funções a seguir, encontre o domínio e o intervalo.

$f(x)=\dfrac{3x−1}{5x+2}$
$f(x)=\sqrt{4−x^2}$

Solução

1. Não é possível dividir por zero, então o domínio é o conjunto de números reais$x$ como esse$x≠−2/5$. Para encontrar o intervalo, precisamos encontrar os valores$y$ para os quais existe um número real$x$ tal que

$y=\dfrac{3x−1}{5x+2}$

Quando multiplicamos os dois lados dessa equação por$5x+2$, vemos que$x$ deve satisfazer a equação

$5xy+2y=3x−1.$

A partir dessa equação, podemos ver que$x$ deve satisfazer

$2y+1=x(3−5y).$

Se y=$3/5$, essa equação não tem solução. Por outro lado, desde que$y≠3/5$,

$x=\dfrac{2y+1}{3−5y}$

satisfaz essa equação. Podemos concluir que o intervalo de$f$ é$\{y\,|\,y≠3/5\}$.

2. Para encontrar o domínio do$f$, precisamos$4−x^2≥0$. Quando consideramos, escrevemos$4−x^2=(2−x)(2+x)≥0$. Essa desigualdade se mantém se e somente se ambos os termos forem positivos ou ambos os termos forem negativos. Para que ambos os termos sejam positivos, precisamos descobrir$x$ que

$2−x≥0$e$2+x≥0.$

Essas duas desigualdades se reduzem para$2≥x$$x≥−2$ e. Portanto, o conjunto$\{x\,|\,−2≤x≤2\}$ deve fazer parte do domínio. Para que ambos os termos sejam negativos, precisamos

$2−x≤0$e$2+x\le 0.$

Essas duas desigualdades também se reduzem para$2≤x$$x\le −2$ e. Não há valores$x$ que satisfaçam essas duas desigualdades. Assim, podemos concluir que o domínio dessa função é$\{x\,|\,−2≤x≤2\}.$

Se$−2≤x≤2$, então$0≤4−x^2≤4$. Portanto$0≤\sqrt{4−x2}≤2$, e o intervalo de$f$ é$\{y\,|\,0≤y≤2\}.$

Exercício$\PageIndex{3}$

Encontre o domínio e o intervalo da função$f(x)=(5x+2)/(2x−1).$

Dica: O denominador não pode ser zero. Resolva a equação de$y=(5x+2)/(2x−1)$$x$ para encontrar o intervalo.
Responda: O domínio é o conjunto de números reais$x$ como esse$x≠1/2$. O alcance é o conjunto$\{y\,|\,y≠5/2\}$.

As funções raiz$f(x)=x^{1/n}$ têm características definidoras, dependendo se$n$ são pares ou ímpares. Para todos os números inteiros$n≥2$ pares, o domínio de$f(x)=x^{1/n}$ é o intervalo$[0,∞)$. Para todos os números inteiros ímpares$n≥1$, o domínio de$f(x)=x^{1/n}$ é o conjunto de todos os números reais. Já que$x^{1/n}=(−x)^{1/n}$ para números inteiros ímpares$n$,$f(x)=x^{1/n}$ é uma função ímpar se$n$ for ímpar. Veja os gráficos das funções raiz para diferentes valores de$n$ na Figura$\PageIndex{7}$.

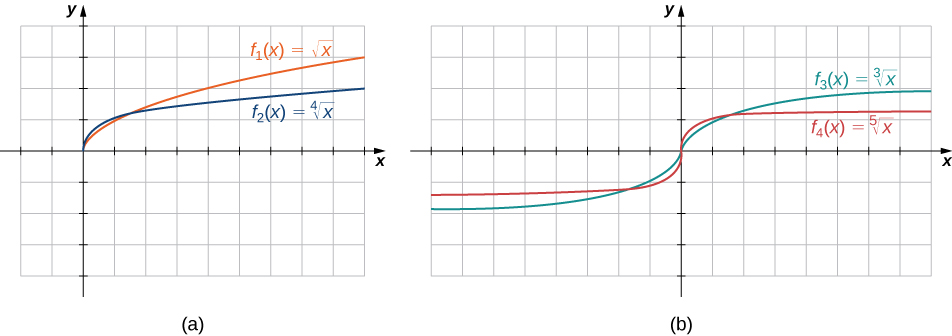
Uma imagem de dois gráficos. O primeiro gráfico é rotulado como “a” e tem um eixo x que vai de -2 a 9 e um eixo y que vai de -4 a 4. O primeiro gráfico é de duas funções. A primeira função é “f (x) = raiz quadrada de x”, que é uma função curva que começa na origem e aumenta. A segunda função é “f (x) = x até a 4ª raiz”, que é uma função curva que começa na origem e aumenta, mas aumenta a uma taxa mais lenta do que a primeira função. O segundo gráfico é denominado “b” e tem um eixo x que vai de -8 a 8 e um eixo y que vai de -4 a 4. O segundo gráfico é de duas funções. A primeira função é “f (x) = raiz cúbica de x”, que é uma função curva que aumenta até a origem, se torna vertical na origem e depois aumenta novamente após a origem. A segunda função é “f (x) = x até a 5ª raiz”, que é uma função curva que aumenta até a origem, se torna vertical na origem e depois aumenta novamente após a origem, mas aumenta a uma taxa mais lenta do que a primeira função. — Figura$\PageIndex{7}$: (a) Se$n$ for par, o domínio de$f(x)=\sqrt[n]{x}$ é$[0,∞)$. (b) Se$n$ for ímpar, o domínio de$f(x)=\sqrt[n]{x}$ é$(−∞,∞)$ e a função$f(x)=\sqrt[n]{x}$ é uma função ímpar.

Exemplo$\PageIndex{6}$: Finding Domains for Algebraic Functions

Para cada uma das funções a seguir, determine o domínio da função.

$f(x)=\dfrac{3}{x^2−1}$
$f(x)=\dfrac{2x+5}{3x^2+4}$
$f(x)=\sqrt{4−3x}$
$f(x)=\sqrt[3]{2x−1}$

Solução

Você não pode dividir por zero, então o domínio é o conjunto de valores$x$ tal que$x^2−1≠0$. Portanto, o domínio é$\{x\,|\,x≠±1\}$.
Você precisa determinar os valores dos$x$ quais o denominador é zero. Já que$3x^2+4≥4$ para todos os números reais$x$, o denominador nunca é zero. Portanto, o domínio é$(−∞,∞).$
Como a raiz quadrada de um número negativo não é um número real, o domínio é o conjunto de valores$x$ para o qual$4−3x≥0$. Portanto, o domínio é$\{x\,|\,x≤4/3\}.$
A raiz cúbica é definida para todos os números reais, então o domínio é o intervalo$(−∞, ∞).$

Exercício$\PageIndex{4}$

Encontre o domínio para cada uma das seguintes funções:$f(x)=(5−2x)/(x^2+2)$$g(x)=\sqrt{5x−1}$ e.

Dica: Determine os valores de$x$ quando a expressão no denominador de$f$ é diferente de zero e encontre os valores de$x$ quando a expressão dentro do radical de não$g$ é negativa.

Responda: O domínio de$f$ é$(−∞, ∞)$. O domínio de$g$ é$\{x\,|\,x≥1/5\}.$

Funções transcendentais

Até agora, discutimos as funções algébricas. Algumas funções, entretanto, não podem ser descritas por operações algébricas básicas. Essas funções são conhecidas como funções transcendentais porque dizem que “transcendem” ou vão além da álgebra. As funções transcendentais mais comuns são as funções trigonométricas, exponenciais e logarítmicas. Uma função trigonométrica relaciona as proporções de dois lados de um triângulo reto. Eles são$\sin x, \cos x, \tan x, \cot x, \sec x,\text{ and }\csc x.$ (discutiremos as funções trigonométricas mais adiante neste capítulo.) Uma função exponencial é uma função da forma$f(x)=b^x$, onde a base$b>0,\, b≠1$. Uma função logarítmica é uma função da forma$f(x)=\log_b(x)$ de alguma constante$b>0,\,b≠1,$ onde$\log_b(x)=y$ se e somente se$b^y=x$. (Também discutiremos as funções exponenciais e logarítmicas posteriormente neste capítulo.)

Exemplo$\PageIndex{7}$: Classifying Algebraic and Transcendental Functions

Classifique cada uma das seguintes funções, a. a c., como algébrica ou transcendental.

$f(x)=\dfrac{\sqrt{x^3+1}}{4x+2}$
$f(x)=2^{x^2}$
$ f(x)=\sin(2x)$

Solução

Como essa função envolve apenas operações algébricas básicas, ela é uma função algébrica.
Essa função não pode ser escrita como uma fórmula que envolve apenas operações algébricas básicas, por isso é transcendental. (Observe que as funções algébricas só podem ter potências que sejam números racionais.)
Como na parte b, essa função não pode ser escrita usando uma fórmula envolvendo apenas operações algébricas básicas; portanto, essa função é transcendental.

Exercício$\PageIndex{5}$:

É$f(x)=x/2$ uma função algébrica ou transcendental?

Responda: Algébrico

Funções definidas por partes

Às vezes, uma função é definida por diferentes fórmulas em diferentes partes de seu domínio. Uma função com essa propriedade é conhecida como função definida por partes. A função de valor absoluto é um exemplo de uma função definida por partes porque a fórmula muda com o sinal de$x$:

\[f(x)=\begin{cases}−x, & \text{if } x<0\\x, & \text{if } x≥0\end{cases}. \nonumber \]

Outras funções definidas por partes podem ser representadas por fórmulas completamente diferentes, dependendo da parte do domínio em que um ponto se encontra. Para representar graficamente uma função definida por partes, representamos graficamente cada parte da função em seu respectivo domínio, no mesmo sistema de coordenadas. Se a fórmula de uma função for diferente para$x<a$ e$x>a$, precisamos prestar atenção especial ao que acontece$x=a$ quando representamos graficamente a função. Às vezes, o gráfico precisa incluir um círculo aberto ou fechado para indicar o valor da função em$x=a$. Examinaremos isso no próximo exemplo.

Exemplo$\PageIndex{8}$: Graphing a Piecewise-Defined Function

Esboce um gráfico da seguinte função definida por partes:

\[f(x)=\begin{cases}x+3, & \text{if } x<1\\(x−2)^2, & \text{if } x≥1\end{cases} \nonumber \]

Solução

Faça um gráfico da função linear$y=x+3$ no intervalo$(−∞,1)$ e represente graficamente a função quadrática$y=(x−2)^2$ no intervalo$[1,∞)$. Como o valor da função at$x=1$ é dado pela fórmula$f(x)=(x−2)^2$, vemos isso$f(1)=1$. Para indicar isso no gráfico, desenhamos um círculo fechado no ponto$(1,1)$. O valor da função é dado por$f(x)=x+3$ for all$x<1$, mas não em$x=1$. Para indicar isso no gráfico, desenhamos um círculo aberto em$(1,4)$.

Uma imagem de um gráfico. O eixo x vai de -7 a 5 e o eixo y vai de -4 a 6. O gráfico é de uma função que tem duas partes. A primeira peça é uma linha crescente que termina no ponto do círculo aberto (1, 4) e tem o rótulo “f (x) = x + 3, para x < 1”. A segunda peça é parabólica e começa no ponto do círculo fechado (1, 1). Depois do ponto (1, 1), a peça começa a diminuir até que o ponto (2, 0) comece a aumentar. Esta peça tem o rótulo “f (x) = (x - 2) ao quadrado, para x — Figura$\PageIndex{8}$: Essa função definida por partes é linear para$x<1$ e quadrática para$x≥1.$

2) Esboce um gráfico da função

$f(x)=\begin{cases}2−x, & \text{if } x≤2\\x+2, & \text{if } x>2\end{cases}.$

Solução:

Uma imagem de um gráfico. O eixo x vai de -6 a 5 e o eixo y vai de -2 a 7. O gráfico é de uma função que tem duas partes. A primeira peça é uma linha decrescente que termina no ponto do círculo fechado (2, 0) e tem o rótulo “f (x) = 2 - x, para x <= 2. A segunda peça é uma linha crescente e começa no ponto do círculo aberto (2, 4) e tem o rótulo “f (x) = x + 2, para x 2. A função tem um intercepto x em (2, 0) e um intercepto y em (0, 2)." src="https://math.libretexts.org/@api/dek...8509006001.png">

Exemplo$\PageIndex{9}$: Parking Fees Described by a Piecewise-Defined Function

Em uma cidade grande, os motoristas pagam tarifas variáveis pelo estacionamento em uma garagem. Eles são cobrados $10 pela primeira hora ou qualquer parte da primeira hora e um adicional de $2 por cada hora ou parte dela até um máximo de $30 por dia. A garagem está aberta das 6h às 12h.

Escreva uma função definida por partes que descreva o custo de$C$ estacionar na garagem em função das horas estacionadas$x$.
Esboce um gráfico dessa função$C(x).$

Solução

1. Como a garagem está aberta 18 horas por dia, o domínio para esta função é$\{x\,|\,0<x≤18\}$. O custo de estacionar um carro nesta garagem pode ser descrito por partes pela função

\[C(x)=\begin{cases}10, & \text{for } 0<x≤1\\12, & \text{for } 1<x≤2\\14, & \text{for } 2<x≤3\\16, & \text{for } 3<x≤4\\ ⋮\\30, & \text{for } 10<x≤18\end{cases}. \nonumber \]

2. O gráfico da função consiste em vários segmentos de linha horizontal.

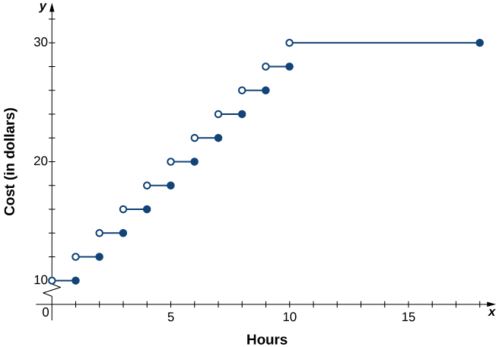
$Uma imagem de um gráfico. O eixo x vai de 0 a 18 e é rotulado como “x, horas”. O eixo y vai de 0 a 32 e é rotulado como “y, custo em dólares”. A função consiste em 11 peças, todos os segmentos de linha horizontal que começam com um círculo aberto e terminam com um círculo fechado. A primeira peça começa em x = 0 e termina em x = 1 e está em y = 10. A segunda peça começa em x = 1 e termina em x = 2 e está em y = 12. A terceira peça começa em x = 2 e termina em x = 3 e está em y = 14. A quarta peça começa em x = 3 e termina em x = 4 e está em y = 16. A quinta peça começa em x = 4 e termina em x = 5 e está em y = 18. A sexta peça começa em x = 5 e termina em x = 6 e está em y = 20. A sétima peça começa em x = 6 e termina em x = 7 e está em y = 22. A oitava peça começa em x = 7 e termina em x = 8 e está em y = 24. A nona peça começa em x = 8 e termina em x = 9 e está em y = 26. A décima peça começa em x = 9 e termina em x = 10 e está em y = 28. A décima primeira peça começa em x = 10 e termina em x = 18 e está em y = 30.$

Exercício$\PageIndex{6}$

O custo do envio de uma carta é uma função do peso da carta. Suponha que o custo do envio de uma carta seja$49¢$ para a primeira onça e$21¢$ para cada onça adicional. Escreva uma função definida por partes descrevendo o custo$C$ em função do peso$x$ de$0<x≤3$, onde$C$ é medido em centavos e$x$ é medido em onças.

Dica: A função definida por partes é constante nos intervalos$(0,1],\,(1,2],\,….$

Responda: \[C(x)=\begin{cases}49, 0<x≤1\\70, 1<x≤2\\91, 2<x≤3\end{cases} \nonumber \]

Transformações de funções

Vimos vários casos em que adicionamos, subtraímos ou multiplicamos constantes para formar variações de funções simples. No exemplo anterior, por exemplo, subtraímos 2 do argumento da função$y=x^2$ para obter a função$f(x)=(x−2)^2$. Essa subtração representa um deslocamento da função$y=x^2$ duas unidades para a direita. Um deslocamento, horizontal ou vertical, é um tipo de transformação de uma função. Outras transformações incluem escalas horizontais e verticais e reflexões sobre os eixos.

Uma mudança vertical de uma função ocorre se somarmos ou subtrairmos a mesma constante em cada saída$y$. Pois$c>0$, o gráfico de$f(x)+c$ é uma mudança do gráfico de$c$ unidades$f(x)$ ascendentes, enquanto o gráfico de$f(x)−c$ é uma mudança do gráfico de$c$ unidades$f(x)$ descendentes. Por exemplo, o gráfico da função$f(x)=x^3+4$ é o gráfico das$4$ unidades$y=x^3$ deslocadas para cima; o gráfico da função$f(x)=x^3−4$ é o gráfico das$4$ unidades$y=x^3$ deslocadas para baixo (Figura$\PageIndex{9}$).

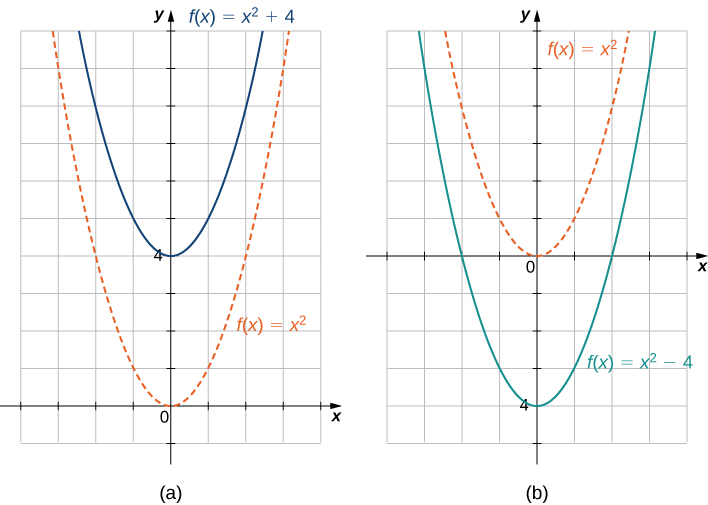
Uma imagem de dois gráficos. O primeiro gráfico é rotulado como “a” e tem um eixo x que vai de -4 a 4 e um eixo y que vai de -1 a 10. O gráfico tem duas funções. A primeira função é “f (x) = x ao quadrado”, que é uma parábola que diminui até a origem e depois aumenta novamente após a origem. A segunda função é “f (x) = (x ao quadrado) + 4”, que é uma parábola que diminui até o ponto (0, 4) e depois aumenta novamente após a origem. As duas funções têm o mesmo formato, mas a segunda função é deslocada para 4 unidades. O segundo gráfico é denominado “b” e tem um eixo x que vai de -4 a 4 e um eixo y que vai de -5 a 6. O gráfico tem duas funções. A primeira função é “f (x) = x ao quadrado”, que é uma parábola que diminui até a origem e depois aumenta novamente após a origem. A segunda função é “f (x) = (x ao quadrado) - 4”, que é uma parábola que diminui até o ponto (0, -4) e depois aumenta novamente após a origem. As duas funções têm o mesmo formato, mas a segunda função é reduzida em 4 unidades. — Figura$\PageIndex{9}$: (a) Para$c>0$, o gráfico de$y=f(x)+c$ é um deslocamento vertical para cima das$c$ unidades do gráfico de$y=f(x)$. (b) Para$c>0$, o gráfico de$y=f(x)−c$ é um deslocamento vertical para baixo c unidades do gráfico de$y=f(x)$.

Um deslocamento horizontal de uma função ocorre se somarmos ou subtrairmos a mesma constante em cada entrada$x$. Pois$c>0$, o gráfico de$f(x+c)$ é um deslocamento do gráfico$f(x)$ para as$c$ unidades da esquerda; o gráfico de$f(x−c)$ é um deslocamento do gráfico das$c$ unidades$f(x)$ para a direita. Por que o gráfico muda para a esquerda ao adicionar uma constante e para a direita ao subtrair uma constante? Para responder a essa pergunta, vamos dar uma olhada em um exemplo.

Considere a função$f(x)=|x+3|$ e avalie essa função em$x−3$. Desde$f(x−3)=|x|$ e$x−3<x$, o gráfico de$f(x)=|x+3|$ é o gráfico das$3$ unidades esquerdas$y=|x|$ deslocadas. Da mesma forma, o gráfico de$f(x)=|x−3|$ é o gráfico das$3$ unidades$y=|x|$ deslocadas para a direita (Figura$\PageIndex{10}$).

Uma imagem de dois gráficos. O primeiro gráfico é rotulado como “a” e tem um eixo x que vai de -8 a 5 e um eixo y que vai de -3 a 5. O gráfico tem duas funções. A primeira função é “f (x) = valor absoluto de x”, que diminui em linha reta até a origem e depois aumenta em linha reta novamente após a origem. A segunda função é “f (x) = valor absoluto de (x + 3)”, que diminui em linha reta até o ponto (-3, 0) e depois aumenta em linha reta novamente após o ponto (-3, 0). As duas funções têm a mesma forma, mas a segunda função é deslocada para a esquerda em 3 unidades. O segundo gráfico é denominado “b” e tem um eixo x que vai de -5 a 8 e um eixo y que vai de -3 a 5. O gráfico tem duas funções. A primeira função é “f (x) = valor absoluto de x”, que diminui em linha reta até a origem e depois aumenta em linha reta novamente após a origem. A segunda função é “f (x) = valor absoluto de (x - 3)”, que diminui em linha reta até o ponto (3, 0) e depois aumenta em linha reta novamente após o ponto (3, 0). As duas funções têm o mesmo formato, mas a segunda função é deslocada para a direita em 3 unidades. — Figura$\PageIndex{10}$: (a) Para$c>0$, o gráfico de$y=f(x+c)$ é um deslocamento horizontal para a esquerda das$c$ unidades do gráfico de$y=f(x)$. (b) Pois$c>0$, o gráfico de$y=f(x−c)$ é um deslocamento horizontal das$c$ unidades direitas do gráfico de$y=f(x).$

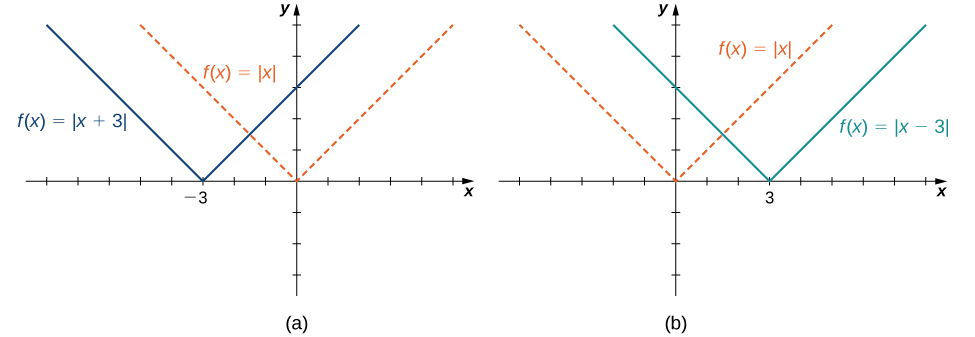
A escala vertical de um gráfico ocorre se multiplicarmos todas as saídas$y$ de uma função pela mesma constante positiva. Pois$c>0$, o gráfico da função$cf(x)$ é o gráfico de$f(x)$ escalado verticalmente por um fator de$c$. Se$c>1$, os valores das saídas da função$cf(x)$ forem maiores do que os valores das saídas da função$f(x)$; portanto, o gráfico foi esticado verticalmente. Se$0<c<1$, então as saídas da função$cf(x)$ são menores, então o gráfico foi compactado. Por exemplo, o gráfico da função$f(x)=3x^2$ é o gráfico de$y=x^2$ esticado verticalmente por um fator de 3, enquanto o gráfico de$f(x)=x^2/3$ é o gráfico de$y=x^2$ comprimido verticalmente por um fator de$3$ (Figura$\PageIndex{11b}$).

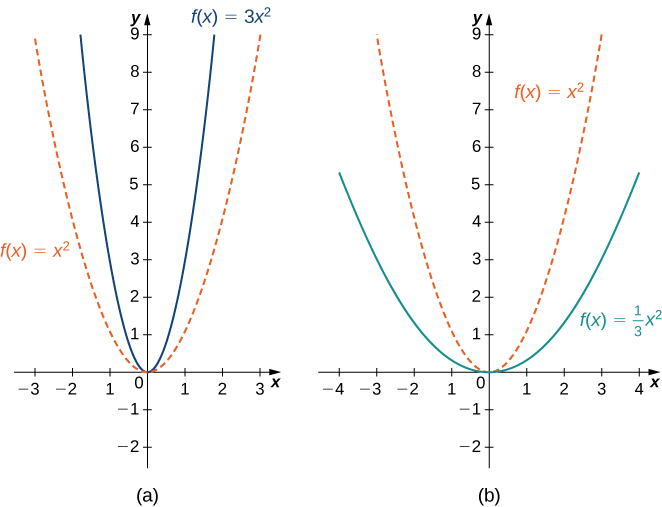
Uma imagem de dois gráficos. O primeiro gráfico é rotulado como “a” e tem um eixo x que vai de -3 a 3 e um eixo y que vai de -2 a 9. O gráfico tem duas funções. A primeira função é “f (x) = x ao quadrado”, que é uma parábola que diminui até a origem e depois aumenta novamente após a origem. A segunda função é “f (x) = 3 (x ao quadrado)”, que é uma parábola que diminui até a origem e depois aumenta novamente após a origem, mas é esticada verticalmente e, portanto, aumenta a uma taxa mais rápida do que a primeira função. O segundo gráfico é denominado “b” e tem um eixo x que vai de -4 a 4 e um eixo y que vai de -2 a 9. O gráfico tem duas funções. A primeira função é “f (x) = x ao quadrado”, que é uma parábola que diminui até a origem e depois aumenta novamente após a origem. A segunda função é “f (x) = (1/3) (x ao quadrado)”, que é uma parábola que diminui até a origem e depois aumenta novamente após a origem, mas é comprimida verticalmente e, portanto, aumenta a uma taxa mais lenta do que a primeira função. — Figura$\PageIndex{11}$: (a) Se$c>1$, o gráfico de$y=cf(x)$ é um trecho vertical do gráfico de$y=f(x)$. (b) Se$0<c<1$, o gráfico de$y=cf(x)$ é uma compressão vertical do gráfico de$y=f(x)$.

A escala horizontal de uma função ocorre se multiplicarmos as entradas$x$ pela mesma constante positiva. Pois$c>0$, o gráfico da função$f(cx)$ é o gráfico de$f(x)$ escalado horizontalmente por um fator de$c$. Se$c>1$, o gráfico de$f(cx)$ é o gráfico de$f(x)$ comprimido horizontalmente. Se$0<c<1$, o gráfico de$f(cx)$ é o gráfico de$f(x)$ esticado horizontalmente. Por exemplo, considere a função$f(x)=\sqrt{2x}$ e avalie$f$ em$x/2$. Uma vez que$f(x/2)=\sqrt{x}$, o gráfico de$f(x)=\sqrt{2x}$ é o gráfico de$y=\sqrt{x}$ comprimido horizontalmente. O gráfico de$y=\sqrt{x/2}$ é um trecho horizontal do gráfico de$y=\sqrt{x}$ (Figura$\PageIndex{12}$).

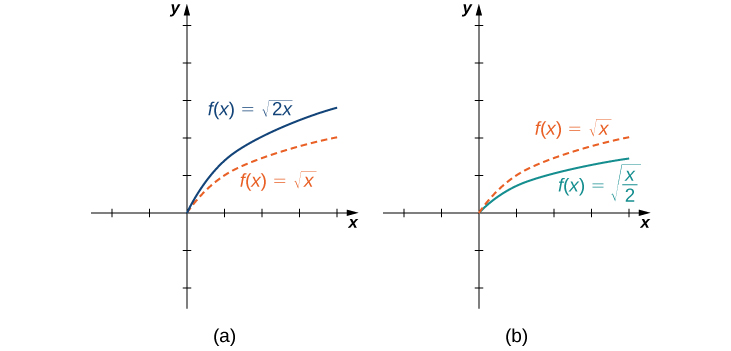
Uma imagem de dois gráficos. Ambos os gráficos têm um eixo x que vai de -2 a 4 e um eixo y que vai de -2 a 5. O primeiro gráfico é rotulado como “a” e tem duas funções. O primeiro gráfico é de duas funções. A primeira função é “f (x) = raiz quadrada de x”, que é uma função curva que começa na origem e aumenta. A segunda função é “f (x) = raiz quadrada de 2x”, que é uma função curva que começa na origem e aumenta, mas aumenta a uma taxa mais rápida do que a primeira função. O segundo gráfico é rotulado como “b” e tem duas funções. A primeira função é “f (x) = raiz quadrada de x”, que é uma função curva que começa na origem e aumenta. A segunda função é “f (x) = raiz quadrada de (x/2)”, que é uma função curva que começa na origem e aumenta, mas aumenta a uma taxa mais lenta do que a primeira função. — Figura$\PageIndex{12}$: (a) Se$c>1$, o gráfico de$y=f(cx)$ é uma compressão horizontal do gráfico de$y=f(x)$. (b) Se$0<c<1$, o gráfico de$y=f(cx)$ é um trecho horizontal do gráfico de$y=f(x)$.

Exploramos o que acontece com o gráfico de uma função$f$ quando multiplicamos$f$ por uma constante$c>0$ para obter uma nova função$cf(x)$. Também discutimos o que acontece com o gráfico de uma função$f$ quando multiplicamos a variável independente$x$ por$c>0$ para obter uma nova função$f(cx)$. No entanto, não abordamos o que acontece com o gráfico da função se a constante$c$ for negativa. Se tivermos uma constante$c<0$, podemos escrever$c$ como um número positivo multiplicado por$−1$; mas, que tipo de transformação obtemos quando multiplicamos a função ou seu argumento por$−1?$ Quando multiplicamos todas as saídas por$−1$, obtemos uma reflexão sobre o$x$ eixo. Quando multiplicamos todas as entradas por$−1$, obtemos uma reflexão sobre o$y$ eixo y. Por exemplo, o gráfico de$f(x)=−(x^3+1)$ é o gráfico$y=(x^3+1)$ refletido sobre o$x$ eixo -. O gráfico de$f(x)=(−x)^3+1$ é o gráfico$y=x^3+1$ refletido sobre o$y$ eixo -( Figura$\PageIndex{13}$).

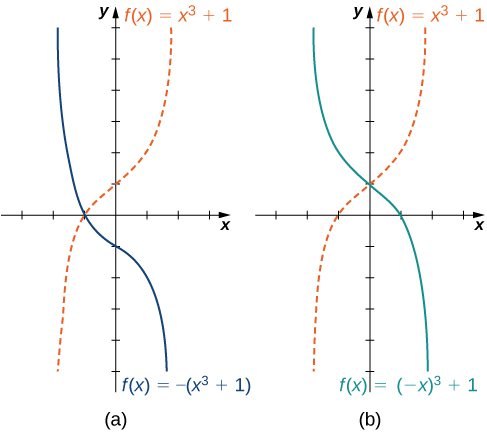
Uma imagem de dois gráficos. Ambos os gráficos têm um eixo x que vai de -3 a 3 e um eixo y que vai de -5 a 6. O primeiro gráfico é rotulado como “a” e tem duas funções. O primeiro gráfico é de duas funções. A primeira função é “f (x) = x ao cubo + 1”, que é uma função crescente curva que tem um intercepto x em (-1, 0) e um intercepto y em (0, 1). A segunda função é “f (x) = - (x ao cubo + 1)”, que é uma função decrescente curva que tem um intercepto x em (-1, 0) e um intercepto y em (0, -1). O segundo gráfico é rotulado como “b” e tem duas funções. A primeira função é “f (x) = x ao cubo + 1”, que é uma função crescente curva que tem um intercepto x em (-1, 0) e um intercepto y em (0, 1). A segunda função é “f (x) = (-x) ao cubo + 1”, que é uma função decrescente curva que tem um intercepto x em (1, 0) e um intercepto y em (0, 1). A primeira função aumenta na mesma taxa, a segunda função diminui para os mesmos valores de x. — Figura$\PageIndex{13}$: (a) O gráfico de$y=−f(x)$ é o gráfico$y=f(x)$ refletido sobre o$x$ eixo -. (b) O gráfico de$y=f(−x)$ é o gráfico$y=f(x)$ refletido sobre o$y$ eixo.

Se o gráfico de uma função consistir em mais de uma transformação de outro gráfico, é importante transformar o gráfico na ordem correta. Dada uma função$f(x)$, o gráfico da função relacionada$y=cf(a(x+b))+d$ pode ser obtido a partir do gráfico de$y=f(x)$ executando as transformações na seguinte ordem.

Deslocamento horizontal do gráfico de$y=f(x)$. Se$b>0$, mude para a esquerda. Se$b<0$ mudar para a direita.
Escala horizontal do gráfico de$y=f(x+b)$ por um fator de$|a|$. Se$a<0$, reflita o gráfico sobre o$y$ eixo -.
Escala vertical do gráfico de$y=f(a(x+b))$ por um fator de$|c|$. Se$c<0$, reflita o gráfico sobre o$x$ eixo -.
Deslocamento vertical do gráfico de$y=cf(a(x+b))$. Se$d>0$, mude para cima. Se$d<0$, mude para baixo.

Podemos resumir as diferentes transformações e seus efeitos relacionados no gráfico de uma função na tabela a seguir.

Transformação de$f (c>0)$	Efeito do gráfico de$f$
\ (f (c>0)\)” style="text-align:center; vertical-align:middle; ">$f(x)+c$	\ (f\)” style="text-align:center; vertical-align:middle; "$c$>Unidades verticais para cima
\ (f (c>0)\)” style="text-align:center; vertical-align:middle; ">$f(x)-c$	\ (f\)” style="text-align:center; vertical-align:middle; "$c$>Unidades de deslocamento vertical para baixo
\ (f (c>0)\)” style="text-align:center; vertical-align:middle; ">$f(x+c)$	\ (f\)” style="text-align:center; vertical-align:middle; ">Deslocar para a esquerda em$c$ unidades
\ (f (c>0)\)” style="text-align:center; vertical-align:middle; ">$f(x-c)$	\ (f\)” style="text-align:center; vertical-align:middle; ">Deslocar para a direita em$c$ unidades
\ (f (c>0)\)” style="text-align:center; vertical-align:middle; ">$cf(x)$	\ (f\)” style="alinhamento vertical: médio; "> Estiramento vertical se$c>1$; compressão vertical se$0<c<1$
\ (f (c>0)\)” style="text-align:center; vertical-align:middle; ">$f(cx)$	\ (f\)” style="alinhamento vertical: médio; "> Estiramento horizontal se$0<c<1$; compressão horizontal se$c>1$
\ (f (c>0)\)” style="text-align:center; vertical-align:middle; ">$-f(x)$	\ (f\)” style="text-align:center; vertical-align:middle; ">Reflexão sobre o$x$ eixo -
\ (f (c>0)\)” style="text-align:center; vertical-align:middle; ">$f(-x)$	\ (f\)” style="text-align:center; vertical-align:middle; ">Reflexão sobre o$y$ eixo -

Exemplo$\PageIndex{10}$: Transforming a Function

Para cada uma das seguintes funções, a. e b., esboce um gráfico usando uma sequência de transformações de uma função conhecida.

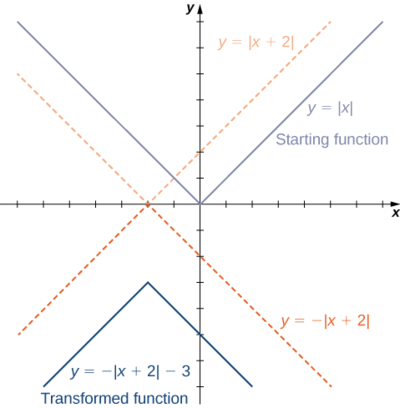
$f(x)=−|x+2|−3$
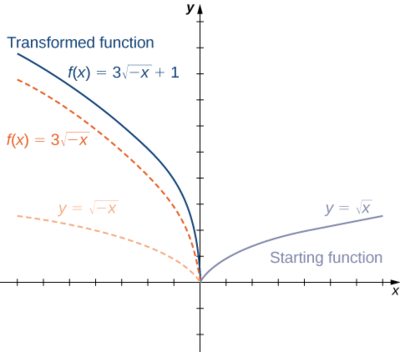
$f(x)=\sqrt[3]{x}+1$

Solução

1. Começando com o gráfico de$y=|x|$, desloque$2$ as unidades para a esquerda, reflita sobre o$x$ eixo -e, em seguida, desloque$3$ as unidades para baixo.

Uma imagem de um gráfico. O eixo x vai de -7 a 7 e um eixo y vai de -7 a 7. O gráfico contém quatro funções. A primeira função é “f (x) = valor absoluto de x” e é rotulada como função inicial. Ele diminui em linha reta até a origem e depois aumenta em linha reta novamente após a origem. A segunda função é “f (x) = valor absoluto de (x + 2)”, que diminui em linha reta até o ponto (-2, 0) e depois aumenta em linha reta novamente após o ponto (-2, 0). A segunda função tem a mesma forma da primeira função, mas é deslocada para a esquerda em 2 unidades. A terceira função é “f (x) = - (valor absoluto de (x + 2))”, que aumenta em linha reta até o ponto (-2, 0) e depois diminui em linha reta novamente após o ponto (-2, 0). A terceira função é a segunda função refletida sobre o eixo x. A quarta função é “f (x) = - (valor absoluto de (x + 2)) - 3” e é rotulada como “função transformada”. Ele aumenta em linha reta até o ponto (-2, -3) e depois diminui em linha reta novamente após o ponto (-2, -3). A quarta função é a terceira função deslocada para baixo em 3 unidades. — Figura$\PageIndex{14}$: A função$f(x)=−|x+2|−3$ pode ser vista como uma sequência de três transformações da função$y=|x|$.

2. Começando com o gráfico de$y=sqrt{x},$ reflexão sobre o$y$ eixo -, estique o gráfico verticalmente por um fator de 3 e suba 1 unidade.

Uma imagem de um gráfico. O eixo x vai de -7 a 7 e um eixo y vai de -2 a 10. O gráfico contém quatro funções. A primeira função é “f (x) = raiz quadrada de x” e é chamada de função inicial. É uma função curva que começa na origem e aumenta. A segunda função é “f (x) = raiz quadrada de -x”, que é uma função curva que diminui até atingir a origem, onde para. A segunda função é a primeira função refletida sobre o eixo y. A terceira função é “f (x) = 3 (raiz quadrada de -x)”, que é uma função curva que diminui até atingir a origem, onde para. A terceira função diminui a uma taxa mais rápida do que a segunda função. A quarta função é “f (x) = 3 (raiz quadrada de -x) + 1” e é rotulada como “função transformada”. É uma função curva que diminui até atingir o ponto (0, 1), onde para. A quarta função é a terceira função deslocada para cima em 1 unidade. — Figura$\PageIndex{15}$: A função$f(x)=\sqrt[3]{x}+1$ pode ser vista como uma sequência de três transformações da função$y=\sqrt{x}$.

Exercício$\PageIndex{7}$

Descreva como a função$f(x)=−(x+1)^2−4$ pode ser representada graficamente usando o gráfico de$y=x^2$ e uma sequência de transformações

Responda: Desloque o gráfico$y=x^2$ para a esquerda em 1 unidade, reflita sobre o$x$ eixo -e, em seguida, desloque 4 unidades para baixo.

Conceitos-chave

A função de potência$f(x)=x^n$ é uma função par se n for par e$n≠0$, e é uma função ímpar se$n$ for ímpar.
A função raiz$f(x)=x^{1/n}$ tem o domínio$[0,∞)$ se n for par e o domínio$(−∞,∞)$ if$n$ for ímpar. Se$n$ for ímpar, então$f(x)=x^{1/n}$ é uma função ímpar.
O domínio da função racional$f(x)=p(x)/q(x)$, onde$p(x)$ e$q(x)$ são funções polinomiais, é o conjunto de$x$ tais que$q(x)≠0$.
Funções que envolvem as operações básicas de adição, subtração, multiplicação, divisão e potências são funções algébricas. Todas as outras funções são transcendentais. Funções trigonométricas, exponenciais e logarítmicas são exemplos de funções transcendentais.
Uma função polinomial$f$ com grau$n≥1$ satisfaz$f(x)→±∞$ como$x→±∞$. O sinal da saída$x→∞$ depende apenas do sinal do coeficiente principal e se$n$ é par ou ímpar.
Desvios verticais e horizontais, escalas verticais e horizontais e reflexões sobre os$y$ eixos$x$ - e -são exemplos de transformações de funções.

Equações-chave

Equação ponto-declive de uma reta\[y−y_1=m(x−x_1)\nonumber \]
Forma de interceptação de inclinação de uma linha\[y=mx+b\nonumber \]
Forma padrão de uma linha\[ax+by=c\nonumber \]
Função polinomial\[f(x)=a_n{x^n}+a_{n−1}x^{n−1}+⋯+a_1x+a_0\nonumber \]

Glossário

função algébrica: uma função envolvendo qualquer combinação apenas das operações básicas de adição, subtração, multiplicação, divisão, potências e raízes aplicadas a uma variável de entrada$x$

função cúbica: um polinômio de grau 3; ou seja, uma função da forma$f(x)=ax^3+bx^2+cx+d$, onde$a≠0$

diploma: para uma função polinomial, o valor do maior expoente de qualquer termo

função linear: uma função que pode ser escrita no formulário$f(x)=mx+b$

função logarítmica: uma função do formulário$f(x)=\log_b(x)$ para alguma base$b>0,\,b≠1$ tal que$y=\log_b(x)$ se e somente se$b^y=x$

modelo matemático: Um método para simular situações da vida real com equações matemáticas

função definida por partes: uma função que é definida de forma diferente em diferentes partes de seu domínio

equação ponto-inclinação: equação de uma função linear indicando sua inclinação e um ponto no gráfico da função

função polinomial: uma função do formulário$f(x)=a_nx^n+a_{n−1}x^{n−1}+…+a_1x+a_0$

função de alimentação: uma função da forma$f(x)=x^n$ para qualquer número inteiro positivo$n≥1$

função quadrática: um polinômio de grau 2; ou seja, uma função da forma$f(x)=ax^2+bx+c$ em que$a≠0$

função racional: uma função da forma$f(x)=p(x)/q(x)$, onde$p(x)$ e$q(x)$ são polinômios

função raiz: uma função do formulário$f(x)=x^{1/n}$ para qualquer número inteiro$n≥2$

inclinação: a mudança em$y$ para cada mudança de unidade em$x$

forma de interceptação de inclinação: equação de uma função linear indicando sua inclinação e$y$ intercepto

função transcendental: uma função que não pode ser expressa por uma combinação de operações aritméticas básicas

transformação de uma função: uma mudança, escala ou reflexão de uma função

Transformação de\(f (c>0)\)	Efeito do gráfico de\(f\)
\ (f (c>0)\)” style="text-align:center; vertical-align:middle; ">\(f(x)+c\)	\ (f\)” style="text-align:center; vertical-align:middle; "\(c\)>Unidades verticais para cima
\ (f (c>0)\)” style="text-align:center; vertical-align:middle; ">\(f(x)-c\)	\ (f\)” style="text-align:center; vertical-align:middle; "\(c\)>Unidades de deslocamento vertical para baixo
\ (f (c>0)\)” style="text-align:center; vertical-align:middle; ">\(f(x+c)\)	\ (f\)” style="text-align:center; vertical-align:middle; ">Deslocar para a esquerda em\(c\) unidades
\ (f (c>0)\)” style="text-align:center; vertical-align:middle; ">\(f(x-c)\)	\ (f\)” style="text-align:center; vertical-align:middle; ">Deslocar para a direita em\(c\) unidades
\ (f (c>0)\)” style="text-align:center; vertical-align:middle; ">\(cf(x)\)	\ (f\)” style="alinhamento vertical: médio; "> Estiramento vertical se\(c>1\); compressão vertical se\(0<c<1\)
\ (f (c>0)\)” style="text-align:center; vertical-align:middle; ">\(f(cx)\)	\ (f\)” style="alinhamento vertical: médio; "> Estiramento horizontal se\(0<c<1\); compressão horizontal se\(c>1\)
\ (f (c>0)\)” style="text-align:center; vertical-align:middle; ">\(-f(x)\)	\ (f\)” style="text-align:center; vertical-align:middle; ">Reflexão sobre o\(x\) eixo -
\ (f (c>0)\)” style="text-align:center; vertical-align:middle; ">\(f(-x)\)	\ (f\)” style="text-align:center; vertical-align:middle; ">Reflexão sobre o\(y\) eixo -

Definição: Inclinação de uma função linear

Definição: Equação de Ponto-Inclinação e Forma de Intercepção de Inclinação e Forma Padrão da Equação de uma Reta

Exemplo\(\PageIndex{1}\): Finding the Slope and Equations of Lines

Exercício\(\PageIndex{1}\)

Exemplo\(\PageIndex{2}\):

A fórmula quadrática

Exemplo\(\PageIndex{3}\): Graphing Polynomial Functions

Exercício\(\PageIndex{2}\)

Exemplo\(\PageIndex{4}\): Maximizing Revenue

Exemplo\(\PageIndex{5}\): Finding Domain and Range for Algebraic Functions

Exercício\(\PageIndex{3}\)

Exemplo\(\PageIndex{6}\): Finding Domains for Algebraic Functions

Exercício\(\PageIndex{4}\)

Exemplo\(\PageIndex{7}\): Classifying Algebraic and Transcendental Functions

Exercício\(\PageIndex{5}\):

Exemplo\(\PageIndex{8}\): Graphing a Piecewise-Defined Function

Exemplo\(\PageIndex{9}\): Parking Fees Described by a Piecewise-Defined Function

Exercício\(\PageIndex{6}\)

Exemplo\(\PageIndex{10}\): Transforming a Function

Exercício\(\PageIndex{7}\)