1.1: Revisão das funções
- Page ID
- 188672
- Use a notação funcional para avaliar uma função.
- Determine o domínio e o alcance de uma função.
- Desenhe o gráfico de uma função.
- Encontre os zeros de uma função.
- Reconheça uma função de uma tabela de valores.
- Crie novas funções a partir de duas ou mais funções dadas.
- Descreva as propriedades de simetria de uma função.
Nesta seção, fornecemos uma definição formal de uma função e examinamos várias maneiras pelas quais as funções são representadas, ou seja, por meio de tabelas, fórmulas e gráficos. Estudamos notação formal e termos relacionados a funções. Também definimos composição de funções e propriedades de simetria. A maior parte desse material será uma revisão para você, mas serve como uma referência útil para lembrá-lo de algumas das técnicas algébricas úteis para trabalhar com funções.
Funções
Dados dois conjuntos\(A\) e\(B\) um conjunto com elementos que são pares ordenados,\((x,y)\) onde\(x\) é um elemento de\(A\) e\(y\) é um elemento de\(B,\) é uma relação de\(A\) para\(B\). Uma relação de\(A\) para\(B\) define uma relação entre esses dois conjuntos. Uma função é um tipo especial de relação em que cada elemento do primeiro conjunto está relacionado a exatamente um elemento do segundo conjunto. O elemento do primeiro conjunto é chamado de entrada; o elemento do segundo conjunto é chamado de saída. As funções são usadas o tempo todo em matemática para descrever relações entre dois conjuntos. Para qualquer função, quando conhecemos a entrada, a saída é determinada, então dizemos que a saída é uma função da entrada. Por exemplo, a área de um quadrado é determinada pelo comprimento do lado, então dizemos que a área (a saída) é uma função do comprimento do lado (a entrada). A velocidade de uma bola lançada no ar pode ser descrita como uma função da quantidade de tempo que a bola está no ar. O custo do envio de um pacote é uma função do peso do pacote. Como as funções têm muitos usos, é importante ter definições e terminologia precisas para estudá-las.

Uma função\(f\) consiste em um conjunto de entradas, um conjunto de saídas e uma regra para atribuir cada entrada a exatamente uma saída. O conjunto de entradas é chamado de domínio da função. O conjunto de saídas é chamado de intervalo da função.
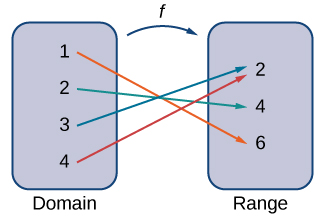
Por exemplo, considere a função\(f\), em que o domínio é o conjunto de todos os números reais e a regra é o quadrado da entrada. Em seguida, a entrada\(x=3\) é atribuída à saída\(3^2=9\).
Como todo número real não negativo tem uma raiz quadrada de valor real, todo número não negativo é um elemento do intervalo dessa função. Como não há um número real com um quadrado negativo, os números reais negativos não são elementos do intervalo. Concluímos que o intervalo é o conjunto de números reais não negativos.
Para uma função geral\(f\) com domínio\(D\), geralmente usamos\(x\) para denotar a entrada e\(y\) para denotar a saída associada\(x\) a. Ao fazer isso, nos referimos\(x\) como variável independente e\(y\) como variável dependente, porque depende de\(x\). Usando a notação de função\(y=f(x)\), escrevemos e lemos essa equação como “\(y\)igual\(f\) a”\(x.”\) Para a função quadrada descrita anteriormente, escrevemos\(f(x)=x^2\).
O conceito de uma função pode ser visualizado usando Figuras\(\PageIndex{1}\) -\(\PageIndex{3}\).
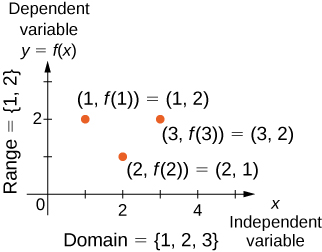
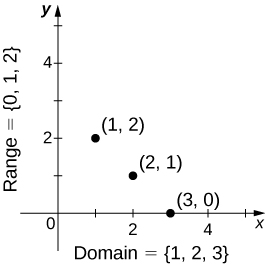
Também podemos visualizar uma função traçando pontos\((x,y)\) no plano de coordenadas onde\(y=f(x)\). O gráfico de uma função é o conjunto de todos esses pontos. Por exemplo, considere a função\(f\), em que o domínio é o conjunto\(D=\{1,2,3\}\) e a regra é\(f(x)=3−x\). Na Figura\(\PageIndex{4}\), traçamos um gráfico dessa função.
Cada função tem um domínio. No entanto, às vezes uma função é descrita por uma equação, como em\(f(x)=x^2\), sem nenhum domínio específico fornecido. Nesse caso, o domínio é considerado o conjunto de todos os números reais\(x\) para os quais\(f(x)\) é um número real. Por exemplo, como qualquer número real pode ser quadrado, se nenhum outro domínio for especificado, consideramos o domínio de\(f(x)=x^2\) como o conjunto de todos os números reais. Por outro lado, a função de raiz quadrada\(f(x)=\sqrt{x}\) só fornece uma saída real se não\(x\) for negativa. Portanto, o domínio da função\(f(x)=\sqrt{x}\) é o conjunto de números reais não negativos, às vezes chamado de domínio natural.
Para as funções\(f(x)=x^2\) e\(f(x)=\sqrt{x}\), os domínios são conjuntos com um número infinito de elementos. Claramente, não podemos listar todos esses elementos. Ao descrever um conjunto com um número infinito de elementos, geralmente é útil usar o construtor de conjuntos ou a notação de intervalo. Ao usar a notação set-builder para descrever um subconjunto de todos os números reais\(R\), indicados, escrevemos
\[\{x\,|\,\textit{x has some property}\}. \nonumber \]
Lemos isso como o conjunto de números\(x\) reais que\(x\) têm alguma propriedade. Por exemplo, se estivéssemos interessados no conjunto de números reais maiores que um, mas menores que cinco, poderíamos denotar esse conjunto usando a notação do construtor de conjuntos escrevendo
\[\{x\,|\,1<x<5\}.\nonumber \]
Um conjunto como esse, que contém todos os números maiores\(a\) e menores que, também\(b,\) pode ser indicado usando a notação de intervalo\((a,b)\). Portanto,
\[(1,5)=\{x\,|\,1<x<5\}.\nonumber \]
Os números\(1\) e\(5\) são chamados de pontos finais desse conjunto. Se quisermos considerar o conjunto que inclui os endpoints, denotaríamos esse conjunto escrevendo
\[[1,5]=\{x\,|\,1 \le x \le 5\}.\nonumber \]
Podemos usar uma notação semelhante se quisermos incluir um dos endpoints, mas não o outro. Para denotar o conjunto de números reais não negativos, usaríamos a notação do construtor de conjuntos
\[\{x\,|\,x\ge 0\}.\nonumber \]
O menor número desse conjunto é zero, mas esse conjunto não tem um número maior. Usando a notação de intervalo, usaríamos o símbolo\(∞,\) que se refere ao infinito positivo e escreveríamos o conjunto como
\[[0,∞)=\{x\,|\,x\ge 0\}.\nonumber \]
É importante observar que não\(∞\) é um número real. É usado simbolicamente aqui para indicar que esse conjunto inclui todos os números reais maiores ou iguais a zero. Da mesma forma, se quiséssemos descrever o conjunto de todos os números não positivos, poderíamos escrever
\[(−∞,0]=\{x\,|\,x≤0\}.\nonumber \]
Aqui, a notação\(−∞\) se refere ao infinito negativo e indica que estamos incluindo todos os números menores ou iguais a zero, não importa quão pequenos sejam. O conjunto
\[(−∞,∞)=\{\textit{x} \,|\, \textit{x is any real number}\}\nonumber \]
refere-se ao conjunto de todos os números reais. Algumas funções são definidas usando equações diferentes para diferentes partes de seu domínio. Esses tipos de funções são conhecidos como funções definidas por partes. Por exemplo, suponha que desejemos definir uma função\(f\) com um domínio que seja o conjunto de todos os números reais, como\(f(x)=3x+1\) para\(x≥2\) e\(f(x)=x^2\) para\( x<2\). Nós denotamos essa função escrevendo
\[f(x)=\begin{cases} 3x+1, & \text{if } x≥2 \\ x^2, & \text{if } x<2 \end{cases}\nonumber \]
Ao avaliar essa função para uma entrada\(x\), a equação a ser usada depende de se\(x≥2\) ou\(x<2\). Por exemplo, desde então\(5>2\), usamos o fato de que\(f(x)=3x+1\) para\(x≥2\) ver isso\(f(5)=3(5)+1=16\). Por outro lado, para\(x=−1\), usamos o fato de que\(f(x)=x^2\) para\(x<2\) e vemos isso\(f(−1)=1\).
Para a função\(f(x)=3x^2+2x−1\), avalie:
- \(f(−2)\)
- \(f(\sqrt{2})\)
- \(f(a+h)\)
Solução
Substitua o valor fornecido por\(x\) na fórmula por\(f(x)\).
- \(f(−2)=3(−2)^2+2(−2)−1=12−4−1=7\)
- \(f(\sqrt{2})=3(\sqrt{2})^2+2\sqrt{2}−1=6+2\sqrt{2}−1=5+2\sqrt{2}\)
- \(f(a+h)=3(a+h)^2+2(a+h)−1=3(a^2+2ah+h^2)+2a+2h−1=3a^2+6ah+3h^2+2a+2h−1\)
Para\(f(x)=x^2−3x+5\),\(f(1)\) avalie\(f(a+h)\) e.
- Dica
-
Substitua\(1\) e\(a+h\) por\(x\) na fórmula por\(f(x)\).
- Responda
-
\(f(1)=3 \)e\(f(a+h)=a^2+2ah+h^2−3a−3h+5\)
Para cada uma das funções a seguir, determine o domínio i. e o intervalo ii.
- \(f(x)=(x−4)^2+5\)
- \(f(x)=\sqrt{3x+2}−1\)
- \(f(x)=\dfrac{3}{x−2}\)
Solução
a. Considere\(f(x)=(x−4)^2+5.\)
1. Como\(f(x)=(x−4)^2+5\) é um número real para qualquer número real\(x\), o domínio de\(f\) é o intervalo\((−∞,∞)\).
2. Desde então\((x−4)^2≥0\), nós sabemos\(f(x)=(x−4)^2+5≥5\). Portanto, o intervalo deve ser um subconjunto de\(\{y\,|\,y≥5\}.\) Para mostrar que cada elemento desse conjunto está no intervalo, precisamos mostrar que, para um determinado\(y\) conjunto, existe um número real\(x\) tal que\(f(x)=(x−4)^2+5=y\). Resolvendo essa equação,\(x,\) pois vemos que precisamos de\(x\) tal forma
\((x−4)^2=y−5.\)
Essa equação é satisfeita desde que exista um número real\(x\) tal que
\(x−4=±\sqrt{y−5}\)
Desde então\(y≥5\), a raiz quadrada está bem definida. Concluímos que para\(x=4±\sqrt{y−5},\)\(f(x)=y,\) e, portanto, o alcance é\(\{y\,|\,y≥5 \}.\)
b. Considere\(f(x)=\sqrt{3x+2}−1\).
1. Para encontrar o domínio de\(f\), precisamos da expressão\(3x+2≥0\). Resolvendo essa desigualdade, concluímos que o domínio é\(\{x\,|\,x≥−2/3\}.\)
2. Para encontrar a variedade de\(f\), notamos que desde então\(\sqrt{3x+2}≥0,\)\(f(x)=\sqrt{3x+2}−1≥−1\). Portanto, o intervalo de\(f\) deve ser um subconjunto do conjunto\(\{y\,|\,y≥−1\}\). Para mostrar que cada elemento desse conjunto está na faixa de\(f\), precisamos mostrar que, para todos\(y\) neste conjunto, existe um número real\(x\) no domínio, tal que\(f(x)=y.\) Let\(y≥−1.\) Then,\(f(x)=y\) if and only if
\(\sqrt{3x+2}−1=y.\)
Resolvendo essa equação,\(x,\) pois vemos que\(x\) deve resolver a equação
\(\sqrt{3x+2}=y+1.\)
Desde então\(y≥−1\),\(x\) isso poderia existir. Ao quadrado dos dois lados dessa equação, temos\(3x+2=(y+1)^2.\)
Portanto, precisamos
\(3x=(y+1)^2−2,\)
o que implica
\(x=\frac{1}{3}(y+1)^2−\frac{2}{3}.\)
Só precisamos verificar se\(x\) está no domínio de\(f\). Como o domínio de\(f\) consiste em todos os números reais maiores ou iguais a\(\frac{−2}{3}\), e
\(\frac{1}{3}(y+1)^2-\frac{2}{3}≥−\frac{2}{3},\)
existe um\(x\) no domínio de\(f\). Concluímos que o intervalo de\(f\) é\(\{y\,|\,y≥−1\}.\)
c. Considere\(f(x)=\dfrac{3}{x−2}.\)
1. Como\(3/(x−2)\) é definido quando o denominador é diferente de zero, o domínio é\(\{x\,|\,x≠2\}.\)
2. Para encontrar o intervalo de,\(f,\) precisamos encontrar os valores de\(y\) tal forma que exista um número real\(x\) no domínio com a propriedade que
\(\dfrac{3}{x−2}=y.\)
Resolvendo essa equação,\(x,\) pois descobrimos que
\(x=\dfrac{3}{y}+2.\)
Portanto\(y≠0\), desde que exista um número real\(x\) no domínio, tal como\(f(x)=y\). Assim, o alcance é\(\{y\,|\,y≠0\}.\)
Encontre o domínio e o intervalo para\(f(x)=\sqrt{4−2x}+5.\)
- Dica
-
Use\(4−2x≥0\).
- Responda
-
Domínio =\(\{x\,|\,x≤2\}\) e intervalo =\(\{y\,|\,y≥5\}\)
Representando funções
Normalmente, uma função é representada usando uma ou mais das seguintes ferramentas:
- Uma mesa
- Um gráfico
- Uma fórmula
Podemos identificar uma função em cada formulário, mas também podemos usá-las juntas. Por exemplo, podemos traçar em um gráfico os valores de uma tabela ou criar uma tabela a partir de uma fórmula.
Mesas
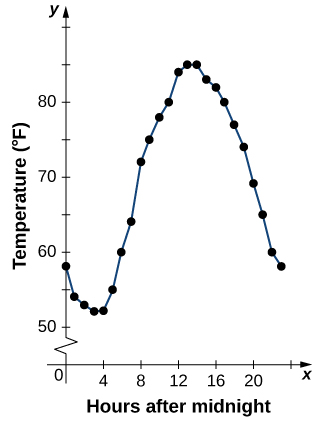
As funções descritas usando uma tabela de valores surgem com frequência em aplicativos reais. Considere o exemplo simples a seguir. Podemos descrever a temperatura em um determinado dia em função da hora do dia. Suponha que gravamos a temperatura a cada hora por um período de 24 horas a partir da meia-noite. Deixamos que nossa variável de entrada\(x\) seja a hora após a meia-noite, medida em horas, e a variável de saída\(y\) seja a temperatura\(x\) horas após a meia-noite, medida em graus Fahrenheit. Registramos nossos dados na Tabela\(\PageIndex{1}\).
| Hora depois da meia-noite | Temperatura (°F) | Hora depois da meia-noite | Temperatura (°F) |
|---|---|---|---|
| 0 | 58 | 12 | 84 |
| 1 | 54 | 13 | 85 |
| 2 | 53 | 14 | 85 |
| 3 | 52 | 15 | 83 |
| 4 | 52 | 16 | 82 |
| 5 | 55 | 17 | 80 |
| 6 | 60 | 18 | 77 |
| 7 | 64 | 19 | 74 |
| 8 | 72 | 20 | 69 |
| 9 | 75 | 21 | 65 |
| 10 | 78 | 22 | 60 |
| 11 | 80 | 23 | 58 |
Podemos ver na tabela que a temperatura é uma função do tempo, e a temperatura diminui, depois aumenta e depois diminui novamente. No entanto, não podemos ter uma visão clara do comportamento da função sem representá-la graficamente.
Gráficos
Dada uma função\(f\) descrita por uma tabela, podemos fornecer uma imagem visual da função na forma de um gráfico. Representar graficamente as temperaturas listadas na Tabela\(\PageIndex{1}\) pode nos dar uma ideia melhor de suas flutuações ao longo do dia. A figura\(\PageIndex{5}\) mostra o gráfico da função de temperatura.
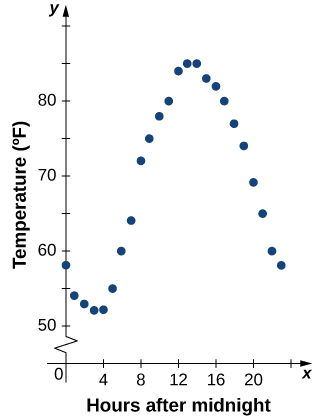
A partir dos pontos traçados no gráfico na Figura\(\PageIndex{5}\), podemos visualizar a forma geral do gráfico. Geralmente, é útil conectar os pontos no gráfico, que representam os dados da tabela. Neste exemplo, embora não possamos fazer nenhuma conclusão definitiva sobre qual era a temperatura em nenhum momento para o qual a temperatura não foi registrada, dado o número de pontos de dados coletados e o padrão nesses pontos, é razoável suspeitar que as temperaturas em outros momentos seguiram um padrão semelhante, como podemos ver na Figura\(\PageIndex{6}\).
Fórmulas algébricas
Às vezes, não recebemos os valores de uma função em forma de tabela, em vez disso, recebemos os valores em uma fórmula explícita. As fórmulas surgem em muitas aplicações. Por exemplo, a área de um círculo de raio\(r\) é dada pela fórmula\(A(r)=πr^2\). Quando um objeto é lançado do solo para cima com uma velocidade inicial em\(v_{0}\) pés/s, sua altura acima do solo desde o momento em que é lançado até atingir o solo é dada pela fórmula\(s(t)=−16t^2+v_{0}t\). Quando os\(P\) dólares são investidos em uma conta a uma taxa de juros anual\(r\) composta continuamente, a quantia de dinheiro após\(t\) anos é dada pela fórmula\(A(t)=Pe^{rt}\). As fórmulas algébricas são ferramentas importantes para calcular os valores das funções. Freqüentemente, também representamos essas funções visualmente em forma de gráfico.
Dada uma fórmula algébrica para uma função\(f\), o gráfico de\(f\) é o conjunto de pontos\((x,f(x))\), onde\(x\) está no domínio de\(f\) e\(f(x)\) está no intervalo. Para representar graficamente uma função dada por uma fórmula, é útil começar usando a fórmula para criar uma tabela de entradas e saídas. Se o domínio de\(f\) consiste em um número infinito de valores, não podemos listar todos eles, mas como listar algumas das entradas e saídas pode ser muito útil, geralmente é uma boa maneira de começar.
Ao criar uma tabela de entradas e saídas, normalmente verificamos se zero é uma saída. Esses valores de\(x\) where\(f(x)=0\) são chamados de zeros de uma função. Por exemplo, os zeros de\(f(x)=x^2−4\) são\(x=±2\). Os zeros determinam onde o gráfico de\(f\) cruza o\(x\) eixo -, o que nos dá mais informações sobre a forma do gráfico da função. O gráfico de uma função pode nunca cruzar o\(x\) eixo -ou pode se cruzar várias (ou até infinitamente muitas) vezes.
Outro ponto de interesse é o\(y\) intercepto -, se existir. O\(y\) intercepto -é dado por\((0,f(0))\).
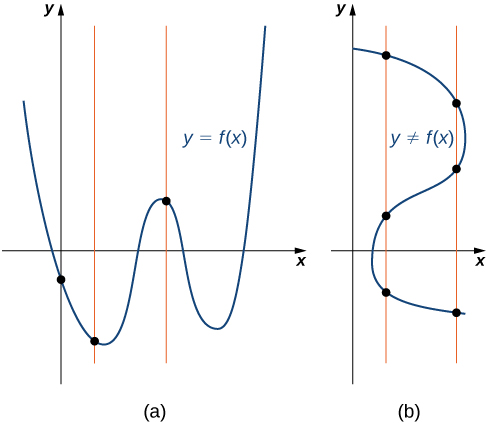
Como uma função tem exatamente uma saída para cada entrada, o gráfico de uma função pode ter, no máximo, um\(y\) intercepto. Se\(x=0\) estiver no domínio de uma função\(f,\), então\(f\) tem exatamente um\(y\) intercepto. Se não\(x=0\) estiver no domínio de\(f,\), então não\(f\) tem\(y\) intercepto. Da mesma forma, para qualquer número real,\(c,\) se\(c\) estiver no domínio de\(f\), há exatamente uma saída\(f(c),\) e a linha\(x=c\) cruza o gráfico de\(f\) exatamente uma vez. Por outro lado, se não\(c\) estiver no domínio de não\(f,\)\(f(c)\) está definido e a linha\(x=c\) não cruza o gráfico de\(f\). Essa propriedade é resumida no teste de linha vertical.
Dada uma função\(f\), cada linha vertical que pode ser desenhada cruza o gráfico de\(f\) no máximo uma vez. Se alguma linha vertical cruzar um conjunto de pontos mais de uma vez, o conjunto de pontos não representa uma função.
Podemos usar esse teste para determinar se um conjunto de pontos representados graficamente representa o gráfico de uma função (Figura\(\PageIndex{7}\)).
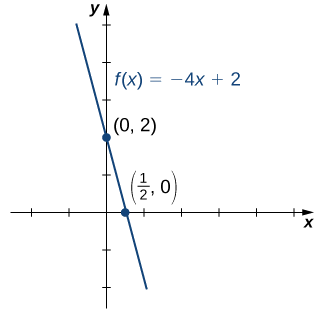
Considere a função\(f(x)=−4x+2.\)
- Encontre todos os zeros de\(f\).
- Encontre o\(y\) -intercept (se houver).
- Esboce um gráfico de\(f\).
Solução
1. Para encontrar os zeros, resolva\(f(x)=−4x+2=0\). Descobrimos que\(f\) tem um zero em\(x=1/2\).
2. O\(y\) intercepto -é dado por\((0,f(0))=(0,2).\)
3. Dado que\(f\) é uma função linear da forma\(f(x)=mx+b\) que passa pelos pontos\((1/2,0)\)\((0,2)\), podemos esboçar o gráfico de\(f\) (Figura\(\PageIndex{8}\)).
Considere a função\(f(x)=\sqrt{x+3}+1\).
- Encontre todos os zeros de\(f\).
- Encontre o\(y\) -intercept (se houver).
- Esboce um gráfico de\(f\).
Solução
1. Para encontrar os zeros, resolva\(\sqrt{x+3}+1=0\). Essa equação implica\(\sqrt{x+3}=−1\). \(\sqrt{x+3}≥0\)Pois, para todos\(x\), essa equação não tem soluções e, portanto, não\(f\) tem zeros.
2. O\(y\) intercepto -é dado por\((0,f(0))=(0,\sqrt{3}+1)\).
3. Para representar graficamente essa função, criamos uma tabela de valores. Como precisamos\(x+3≥0\), precisamos escolher valores de\(x≥−3\). Escolhemos valores que facilitam a avaliação da função de raiz quadrada.
| \(x\) | -3 | -2 | 1 |
|---|---|---|---|
| \(f(x)\) | 1 | 2 | 3 |
Fazendo uso da tabela e sabendo que, como a função é uma raiz quadrada, o gráfico de\(f\) deve ser semelhante ao gráfico de\(y=\sqrt{x}\), esboçamos o gráfico (Figura\(\PageIndex{9}\)).
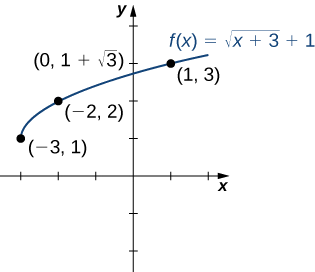
Encontre os zeros de\(f(x)=x^3−5x^2+6x.\)
- Dica
-
Fator o polinômio.
- Responda
-
\(x=0,2,3\)
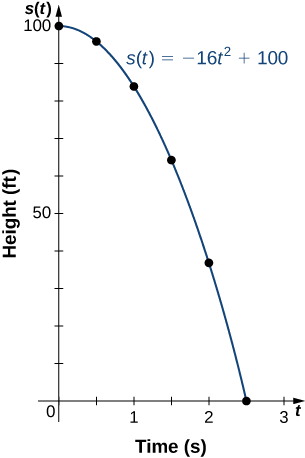
Se uma bola cair de uma altura de 100 pés, sua altura s por vez\(t\) é dada pela função\(s(t)=−16t^2+100\), onde s é medido em pés e\(t\) é medido em segundos. O domínio é restrito ao intervalo\([0,c],\) onde\(t=0\) está o momento em que a bola cai e\(t=c\) é o momento em que a bola atinge o chão.
- Crie uma tabela mostrando a altura s (t) quando\(t=0,\, 0.5,\, 1,\, 1.5,\, 2,\)\(2.5\) e. Usando os dados da tabela, determine o domínio dessa função. Ou seja, encontre a\(c\) hora em que a bola atinge o chão.
- Esboce um gráfico de\(s\).
Solução
| \(t\) | 0 | 0,5 | 1 | 1,5 | 2 | 2,5 |
| \(s(t)\) | 100 | 96 | 84 | 64 | 36 | 0 |
Como a bola atinge o chão quando\(t=2.5\), o domínio dessa função é o intervalo\([0,2.5]\).
2.
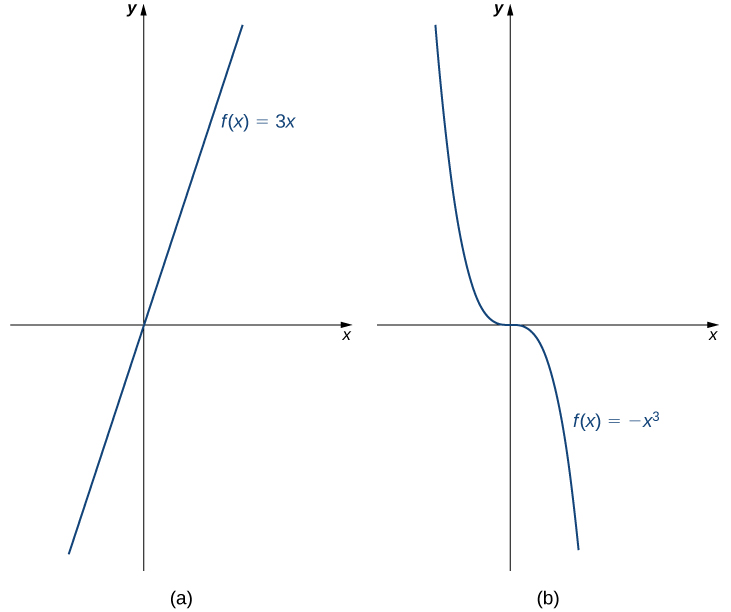
Dizemos que uma função\(f\) está aumentando no intervalo\(I\) se for tudo\(x_{1},\, x_{2}∈I,\)
\(f(x_{1})≤f(x_{2})\)quando\(x_{1}<x_{2}.\)
Dizemos que\(f\) está aumentando estritamente no intervalo,\(I\) se for para todos.\(x_{1},x_{2}∈I,\)
\(f(x_{1})<f(x_{2})\)quando\(x_{1}<x_{2}.\)
Dizemos que uma função\(f\) está diminuindo no intervalo\(I\) se for tudo\(x_{1},x_{2}∈I,\)
\(f(x_{1})≥f(x_{2})\)E se\(x_{1}<x_{2}.\)
Dizemos que uma função\(f\) está diminuindo estritamente no intervalo,\(I\) se para todos\(x_{1},x_{2}∈I\),
\(f(x_{1})>f(x_{2})\)E se\(x_{1}<x_{2}.\)
Por exemplo, a função\(f(x)=3x\) está aumentando no intervalo\((−∞,∞)\) porque\(3x_{1}<3x_{2}\) sempre\(x_{1}<x_{2}\). Por outro lado, a função\(f(x)=−x^3\) está diminuindo no intervalo\((−∞,∞)\) porque\(−x^3_{1}>−x^3_{2}\) sempre\(x_{1}<x_{2}\) (Figura\(\PageIndex{10}\)).
Combinando funções
Agora que analisamos as características básicas das funções, podemos ver o que acontece com essas propriedades quando combinamos funções de maneiras diferentes, usando operações matemáticas básicas para criar novas funções. Por exemplo, se o custo de uma empresa fabricar\(x\) itens for descrito pela função\(C(x)\) e a receita criada pela venda de\(x\) itens for descrita pela função\(R(x)\), o lucro na fabricação e venda de\(x\) itens será definido como\(P(x)=R(x)−C(x)\). Usando a diferença entre duas funções, criamos uma nova função.
Como alternativa, podemos criar uma nova função compondo duas funções. Por exemplo, dadas as funções\(f(x)=x^2\) e\(g(x)=3x+1\), a função composta\(f∘g\) é definida de forma que
\[(f∘g)(x)=f(g(x))=(g(x))^2=(3x+1)^2. \nonumber \]
A função composta\(g∘f\) é definida de forma que
\[(g∘f)(x)=g(f(x))=3f(x)+1=3x^2+1. \nonumber \]
Observe que essas duas novas funções são diferentes uma da outra.
Combinando funções com operadores matemáticos
Para combinar funções usando operadores matemáticos, simplesmente escrevemos as funções com o operador e simplificamos. Dadas duas funções\(f\) e\(g\), podemos definir quatro novas funções:
| \((f+g)(x)=f(x)+g(x)\) | Soma |
| \((f−g)(x)=f(x)−g(x)\) | Diferença |
| \((f·g)(x)=f(x)g(x)\) | Produto |
| \((\frac{f}{g})(x)=\frac{f(x)}{g(x)}\)para\(g(x)≠0\) | Quociente |
Dadas as funções\(f(x)=2x−3\) e\(g(x)=x^2−1\), encontre cada uma das seguintes funções e declare seu domínio.
- \((f+g)(x)\)
- \((f−g)(x)\)
- \((f·g)(x)\)
- \(\left(\dfrac{f}{g}\right)(x)\)
Solução
1. \((f+g)(x)=(2x−3)+(x^2−1)=x^2+2x−4.\)
O domínio dessa função é o intervalo\((−∞,∞)\).
2. \((f−g)(x)=(2x−3)−(x^2−1)=−x^2+2x−2.\)
O domínio dessa função é o intervalo\((−∞,∞)\).
3. \((f·g)(x)=(2x−3)(x^2−1)=2x^3−3x^2−2x+3.\)
O domínio dessa função é o intervalo\((−∞,∞)\).
4. \(\left(\dfrac{f}{g}\right)(x)=\dfrac{2x−3}{x^2−1}\).
O domínio dessa função é\(\{x\,|\,x≠±1\}.\)
Para\(f(x)=x^2+3\) e\(g(x)=2x−5\), encontre\((f/g)(x)\) e declare seu domínio.
- Dica
-
A nova função\((f/g)(x)\) é um quociente de duas funções. Para quais valores de\(x\) é o denominador zero?
- Responda
-
\(\left(\dfrac{f}{g}\right)(x)=\frac{x^2+3}{2x−5}.\)O domínio é\(\{x\,|\,x≠\frac{5}{2}\}.\)
Composição da função
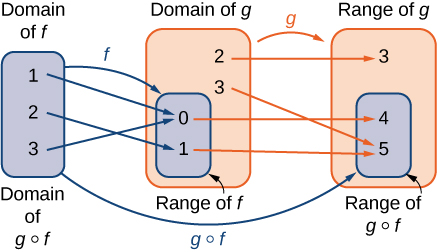
Quando escrevemos funções, assumimos uma função de uma função. Por exemplo, suponha que a temperatura\(T\) em um determinado dia seja descrita como uma função do tempo\(t\) (medida em horas após a meia-noite), como na Tabela\(\PageIndex{1}\). Suponha que o custo\(C\), para aquecer ou resfriar um prédio por 1 hora, possa ser descrito como uma função da temperatura\(T\). Combinando essas duas funções, podemos descrever o custo de aquecimento ou resfriamento de um edifício em função do tempo avaliando\(C(T(t))\). Definimos uma nova função, denotada\(C∘T\), que é definida de forma que\((C∘T)(t)=C(T(t))\) para todos\(t\) no domínio de\(T\). Essa nova função é chamada de função composta. Observamos que, como o custo é uma função da temperatura e a temperatura é uma função do tempo, faz sentido definir essa nova função\((C∘T)(t)\). Não faz sentido considerar\((T∘C)(t)\), porque a temperatura não é uma função do custo.
Considere a função\(f\) com domínio\(A\) e alcance\(B\), e a função\(g\) com domínio\(D\) e intervalo\(E\). Se\(B\) for um subconjunto de\(D\), então a função composta\((g∘f)(x)\) é a função com domínio\(A\) tal que
\[(g∘f)(x)=g(f(x)) \nonumber \]
Uma função composta\(g∘f\) pode ser visualizada em duas etapas. Primeiro, a função\(f\) mapeia cada entrada\(x\) no domínio de\(f\) até sua saída\(f(x)\) no intervalo de\(f\). Segundo, como o intervalo de\(f\) é um subconjunto do domínio de\(g\), a saída\(f(x)\) é um elemento no domínio de e\(g\), portanto, é mapeada para uma saída\(g(f(x))\) na faixa de\(g\). Na Figura\(\PageIndex{11}\), vemos uma imagem visual de uma função composta.
Considere as funções\(f(x)=x^2+1\)\(g(x)=1/x\) e.
- Encontre\((g∘f)(x)\) e declare seu domínio e alcance.
- Avalie\((g∘f)(4),\)\((g∘f)(−1/2)\).
- Encontre\((f∘g)(x)\) e declare seu domínio e alcance.
- Avalie\((f∘g)(4),\)\((f∘g)(−1/2)\).
Solução
1. Podemos encontrar a fórmula para\((g∘f)(x)\) de duas maneiras diferentes. Nós poderíamos escrever
\((g∘f)(x)=g(f(x))=g(x^2+1)=\dfrac{1}{x^2+1}\).
Alternativamente, poderíamos escrever
\((g∘f)(x)=g(f(x))=\dfrac{1}{f(x)}=\dfrac{1}{x^2+1}.\)
Já que\(x^2+1≠0\) para todos os números reais,\(x,\) o domínio de\((g∘f)(x)\) é o conjunto de todos os números reais. Desde então\(0<1/(x^2+1)≤1\), o alcance é, no máximo, o intervalo\((0,1]\). Para mostrar que o intervalo é todo esse intervalo, deixamos\(y=1/(x^2+1)\) e resolvemos essa equação\(x\) para mostrar que, para todos\(y\) no intervalo\((0,1]\), existe um número real\(x\) tal que\(y=1/(x^2+1)\). Resolvendo essa equação,\(x,\) pois vemos isso\(x^2+1=1/y\), o que implica que
\(x=±\sqrt{\frac{1}{y}−1}\)
Se\(y\) estiver no intervalo\((0,1]\), a expressão sob o radical não é negativa e, portanto, existe um número real\(x\) como esse\(1/(x^2+1)=y\). Concluímos que o intervalo de\(g∘f\) é o intervalo\((0,1].\)
2. \((g∘f)(4)=g(f(4))=g(4^2+1)=g(17)=\frac{1}{17}\)
\((g∘f)(−\frac{1}{2})=g(f(−\frac{1}{2}))=g((−\frac{1}{2})^2+1)=g(\frac{5}{4})=\frac{4}{5}\)
3. Podemos encontrar uma fórmula para\((f∘g)(x)\) de duas maneiras. Primeiro, poderíamos escrever
\((f∘g)(x)=f(g(x))=f(\frac{1}{x})=(\frac{1}{x})^2+1.\)
Alternativamente, poderíamos escrever
\((f∘g)(x)=f(g(x))=(g(x))^2+1=(\frac{1}{x})^2+1.\)
O domínio de\(f∘g\) é o conjunto de todos os números reais\(x\), tais como\(x≠0\). Para encontrar o intervalo de,\(f,\) precisamos encontrar todos os valores\(y\) para os quais existe um número real\(x≠0\) tal que
\(\left(\dfrac{1}{x}\right)^2+1=y.\)
Resolvendo essa equação, pois\(x,\) vemos que\(x\) precisamos satisfazer
\(\left(\dfrac{1}{x}\right)^2=y−1,\)
o que simplifica para
\(\dfrac{1}{x}=±\sqrt{y−1}\)
Finalmente, obtemos
\(x=±\dfrac{1}{\sqrt{y−1}}.\)
Uma vez que\(1/\sqrt{y−1}\) é um número real se e somente se\(y>1,\) o intervalo de\(f\) for o definido\(\{y\,|\,y≥1\}.\)
4. \((f∘g)(4)=f(g(4))=f(\frac{1}{4})=(\frac{1}{4})^2+1=\frac{17}{16}\)
\((f∘g)(−\frac{1}{2})=f(g(−\frac{1}{2}))=f(−2)=(−2)^2+1=5\)
No exemplo\(\PageIndex{7}\), podemos ver isso\((f∘g)(x)≠(g∘f)(x)\). Isso nos diz, em termos gerais, que a ordem em que compomos as funções é importante.
Deixe\(f(x)=2−5x\). Deixe\(g(x)=\sqrt{x}.\) encontrar\((f∘g)(x)\).
Solução
\((f∘g)(x)=2−5\sqrt{x}.\)
Considere as funções\(f\)\(g\) descritas por
| \(x\) | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|---|---|---|
| \(f(x)\) | 0 | 4 | 2 | 4 | -2 | 0 | -2 | 4 |
| \(x\) | -4 | -2 | 0 | 2 | 4 |
|---|---|---|---|---|---|
| \(g(x)\) | 1 | 0 | 3 | 0 | 5 |
- Avalie\((g∘f)(3)\),\((g∘f)(0)\).
- Indique o domínio e o intervalo de\((g∘f)(x)\).
- Avalie\((f∘f)(3)\),\((f∘f)(1)\).
- Indique o domínio e o intervalo de\((f∘f)(x)\).
Solução:
1. \((g∘f)(3)=g(f(3))=g(−2)=0\)
\((g∘f)(0)=g(4)=5\)
2. O domínio de\(g∘f\) é o conjunto.\(\{−3,−2,−1,0,1,2,3,4\}.\) Como o intervalo de\(f\) é o conjunto,\(\{−2,0,2,4\},\) o intervalo de\(g∘f\) é o conjunto\(\{0,3,5\}.\)
3. \((f∘f)(3)=f(f(3))=f(−2)=4\)
\((f∘f)(1)=f(f(1))=f(−2)=4\)
4. O domínio de\(f∘f\) é o conjunto\(\{−3,−2,−1,0,1,2,3,4\}.\) Como o intervalo de\(f\) é o conjunto,\(\{−2,0,2,4\},\) o intervalo de\(f∘f\) é o conjunto\(\{0,4\}.\)
Uma loja está anunciando uma venda de 20% de desconto em todas as mercadorias. Caroline tem um cupom que lhe dá direito a um desconto adicional de 15% em qualquer item, incluindo mercadorias em promoção. Se Caroline decidir comprar um item com o preço original de\(x\) dólares, quanto ela acabará pagando se aplicar o cupom ao preço de venda? Resolva esse problema usando uma função composta.
Solução
Como o preço de venda é de 20% sobre o preço original, se um item for em\(x\) dólares, seu preço de venda é dado por\(f(x)=0.80x\). Como o cupom dá direito a um indivíduo a 15% de desconto no preço de qualquer item, se um item for em\(y\) dólares, o preço, após a aplicação do cupom, é dado por g (y) =0,85y. Portanto, se o preço for originalmente em\(x\) dólares, seu preço de venda será\(f(x)=0.80x\) e, em seguida, seu preço final após o cupom será\(g(f(x))=0.85(0.80x)=0.68x\).
Se os itens estiverem à venda com 10% de desconto em relação ao preço original e o cliente tiver um cupom para um desconto adicional de 30%, qual será o preço final de um item originalmente em\(x\) dólares, depois de aplicar o cupom ao preço de venda?
Dica
O preço de venda de um item com um preço original de\(x\) dólares é\(f(x)=0.90x\). O preço do cupom de um item em\(y\) dólares é\(g(y)=0.70y\).
Solução
\((g∘f)(x)=0.63x\)
Simetria de funções
Os gráficos de certas funções têm propriedades de simetria que nos ajudam a entender a função e a forma de seu gráfico. Por exemplo, considere a função\(f(x)=x^4−2x^2−3\) mostrada na Figura\(\PageIndex{12a}\). Se pegarmos a parte da curva que está à direita do\(y\) eixo -e a virarmos sobre o\(y\) eixo -, ela ficará exatamente no topo da curva à esquerda do\(y\) eixo. Nesse caso, dizemos que a função tem simetria em relação ao\(y\) eixo -. Por outro lado, considere a função\(f(x)=x^3−4x\) mostrada na Figura\(\PageIndex{12b}\). Se pegarmos o gráfico e girá-lo em\(180°\) torno da origem, o novo gráfico terá exatamente a mesma aparência. Nesse caso, dizemos que a função tem simetria sobre a origem.
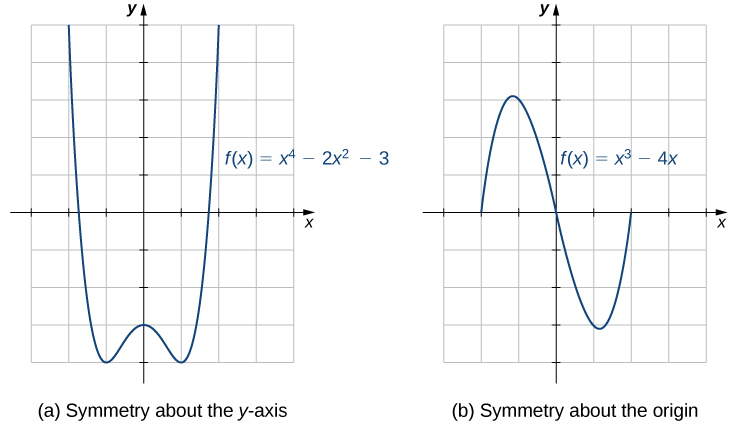
Se recebermos o gráfico de uma função, é fácil ver se o gráfico tem uma dessas propriedades de simetria. Mas sem um gráfico, como podemos determinar algebricamente se uma função\(f\) tem simetria? Olhando para a Figura\(\PageIndex{12a}\) novamente, vemos que, uma vez que\(f\) é simétrico em relação ao\(y\) eixo -, se o ponto\((x,y)\) estiver no gráfico, o ponto\((−x,y)\) está no gráfico. Em outras palavras,\(f(−x)=f(x)\). Se uma função\(f\) tem essa propriedade, dizemos que\(f\) é uma função par, que tem simetria sobre o\(y\) eixo -. Por exemplo,\(f(x)=x^2\) é até porque
\(f(−x)=(−x)^2=x^2=f(x).\)
Em contraste, olhando para a Figura\(\PageIndex{12b}\) novamente, se uma função\(f\) é simétrica em relação à origem, então sempre que o ponto\((x,y)\) está no gráfico, o ponto também\((−x,−y)\) está no gráfico. Em outras palavras,\(f(−x)=−f(x)\). Se\(f\) tem essa propriedade, dizemos que\(f\) é uma função ímpar, que tem simetria sobre a origem. Por exemplo,\(f(x)=x^3\) é estranho porque
\(f(−x)=(−x)^3=−x^3=−f(x).\)
- Se\(f(x)=f(−x)\) para todos\(x\) no domínio de\(f\), então\(f\) é uma função par. Uma função par é simétrica em relação ao\(y\) eixo -.
- Se for\(f(−x)=−f(x)\) para todos\(x\) no domínio de\(f\), então\(f\) é uma função ímpar. Uma função ímpar é simétrica em relação à origem.
Determine se cada uma das funções a seguir é par, ímpar ou nenhuma delas.
- \(f(x)=−5x^4+7x^2−2\)
- \(f(x)=2x^5−4x+5\)
- \(f(x)=\frac{3x}{x^2+1}\)
Solução
Para determinar se uma função é par ou ímpar, nós a avaliamos\(f(−x)\) e comparamos com\(f(x)\)\(−f(x)\) e.
1. \(f(−x)=−5(−x)^4+7(−x)^2−2=−5x^4+7x^2−2=f(x).\)Portanto,\(f\) está empatado.
2. \(f(−x)=2(−x)^5−4(−x)+5=−2x^5+4x+5.\)Agora,\(f(−x)≠f(x).\) além disso, observando isso\(−f(x)=−2x^5+4x−5\), vemos isso\(f(−x)≠−f(x)\). Portanto, não\(f\) é nem par nem ímpar.
3. \(f(−x)=3(−x)/((−x)2+1)\)\(=−3x/(x^2+1)=\)\(−[3x/(x^2+1)]=−f(x).\)Portanto,\(f\) é estranho.
Determine se\(f(x)=4x^3−5x\) é par, ímpar ou nenhum.
- Dica
-
Compare\(f(−x)\) com\(f(x)\)\(−f(x)\) e.
- Responda
-
\(f(x)\)é estranho.
Uma função simétrica que surge com frequência é a função de valor absoluto, escrita como\(|x|\). A função de valor absoluto é definida como
\[f(x)=\begin{cases} -x, & \text{if }x<0 \\ x, & \text{if } x≥0 \end{cases} \nonumber \]
Alguns estudantes descrevem essa função afirmando que ela “torna tudo positivo”. Pela definição da função de valor absoluto, vemos que if\(x<0\), then\(|x|=−x>0,\) e if\(x>0\), então\(|x|=x>0.\) No entanto, para\(x=0,\)\(|x|=0.\) Portanto, é mais preciso dizer que para todas as entradas diferentes de zero, a saída é positiva, mas se\(x=0\), a saída\(|x|=0\). Concluímos que o intervalo da função de valor absoluto é\(\{y\,|\,y≥0\}.\) Na Figura\(\PageIndex{13}\), vemos que a função de valor absoluto é simétrica em relação ao\(y\) eixo -e, portanto, é uma função par.
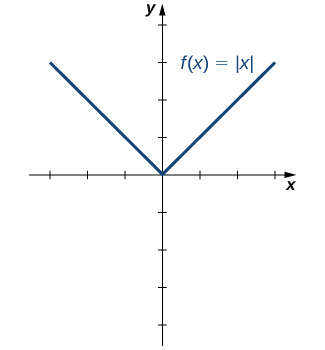
Encontre o domínio e o alcance da função\(f(x)=2|x−3|+4\).
Solução
Como a função de valor absoluto é definida para todos os números reais, o domínio dessa função é\((−∞,∞)\). Já que,\(|x−3|≥0\) para todos\(x\), a função\(f(x)=2|x−3|+4≥4\). Portanto, o intervalo é, no máximo, o conjunto.\(\{y\,|\,y≥4\}.\) Para ver que o intervalo é, de fato, todo esse conjunto, precisamos mostrar que\(y≥4\) existe um número real\(x\) tal que
\(2|x−3|+4=y\)
Um número real\(x\) satisfaz essa equação, desde que
\(|x−3|=\frac{1}{2}(y−4)\)
Como sabemos\(y≥4\), e\(y−4≥0\), portanto, o lado direito da equação não é negativo, então é possível que haja uma solução. Além disso,
\(|x−3|=\begin{cases} −(x−3), & \text{if } x<3\\x−3, & \text{if } x≥3\end{cases}\)
Portanto, vemos que existem duas soluções:
\(x=±\frac{1}{2}(y−4)+3\).
O alcance dessa função é\(\{y\,|\,y≥4\}.\)
Para a função\(f(x)=|x+2|−4\), encontre o domínio e o intervalo.
- Dica
-
\(|x+2|≥0\)para todos os números reais\(x\).
- Responda
-
Domínio =\((−∞,∞)\), intervalo =\(\{y\,|\,y≥−4\}.\)
Conceitos-chave
- Uma função é um mapeamento de um conjunto de entradas para um conjunto de saídas com exatamente uma saída para cada entrada.
- Se nenhum domínio for declarado para uma função,\(y=f(x),\) o domínio é considerado o conjunto de todos os números reais\(x\) para os quais a função está definida.
- Ao desenhar o gráfico de uma função,\(f,\) cada linha vertical pode cruzar o gráfico, no máximo, uma vez.
- Uma função pode ter qualquer número de zeros, mas tem, no máximo, um\(y\) intercepto.
- Para definir a composição\(g∘f\), o intervalo de\(f\) deve estar contido no domínio de\(g\).
- As funções pares são simétricas em relação ao\(y\) eixo -, enquanto as funções ímpares são simétricas em relação à origem.
Equações-chave
- Composição de duas funções
\((g∘f)(x)=g\big(f(x)\big)\)
- Função de valor absoluto
\(f(x)=\begin{cases}−x, & \text{if } x<0\\x, & \text{if } x≥0\end{cases}\)
Glossário
- função de valor absoluto
- \(f(x)=\begin{cases}−x, & \text{if } x<0\\x, & \text{if } x≥0\end{cases}\)
- função composta
- dadas duas funções\(f\) e\(g\), uma nova função, denotada\(g∘f\), tal que\((g∘f)(x)=g(f(x))\)
- diminuindo no intervalo\(I\)
- uma função que diminui no intervalo\(I\) se, para todos,\(x_1,\,x_2∈I,\;f(x_1)≥f(x_2)\) se\(x_1<x_2\)
- variável dependente
- a variável de saída para uma função
- domínio
- o conjunto de entradas para uma função
- função uniforme
- uma função é mesmo que,\(f(−x)=f(x)\) para todos,\(x\) no domínio de\(f\)
- função
- um conjunto de entradas, um conjunto de saídas e uma regra para mapear cada entrada para exatamente uma saída
- gráfico de uma função
- o conjunto de pontos\((x,y)\) que\(x\) está no domínio de\(f\) e\(y=f(x)\)
- aumentando no intervalo\(I\)
- uma função que aumenta no intervalo\(I\) if for all\(x_1,\,x_2∈I,\;f(x_1)≤f(x_2)\) if\(x_1<x_2\)
- variável independente
- a variável de entrada para uma função
- função ímpar
- uma função é ímpar se\(f(−x)=−f(x)\) para todos\(x\) no domínio de\(f\)
- alcance
- o conjunto de saídas para uma função
- simetria sobre a origem
- o gráfico de uma função\(f\) é simétrico em relação à origem se\((−x,−y)\) estiver no gráfico de\(f\) sempre que\((x,y)\) estiver no gráfico
- simetria sobre o\(y\) eixo -
- o gráfico de uma função\(f\) é simétrico em relação ao\(y\) eixo -se\((−x,y)\) estiver no gráfico de\(f\) sempre que\((x,y)\) estiver no gráfico
- tabela de valores
- uma tabela contendo uma lista de entradas e suas saídas correspondentes
- teste de linha vertical
- dado o gráfico de uma função, cada linha vertical cruza o gráfico, no máximo, uma vez
- zeros de uma função
- quando um número real\(x\) é zero de uma função\(f,\;f(x)=0\)


