14.4 : Plans tangents et approximations linéaires
- Page ID
- 197327
- Déterminez l'équation d'un plan tangent à une surface donnée en un point.
- Utilisez le plan tangent pour approximer une fonction de deux variables en un point.
- Expliquez quand une fonction de deux variables est dérivable.
- Utilisez le différentiel total pour approximer la variation d'une fonction de deux variables.
Dans cette section, nous examinons le problème de la détermination du plan tangent à une surface, ce qui est analogue à la recherche de l'équation d'une droite tangente à une courbe lorsque la courbe est définie par le graphe d'une fonction d'une variable,\( y=f(x)\). La pente de la tangente au point\( x=a\) est donnée par\( m=f′(a)\) ; quelle est la pente d'un plan tangent ? Nous avons découvert l'équation d'un plan dans Équations de lignes et de plans dans l'espace ; dans cette section, nous verrons comment elle peut être appliquée au problème en question.
Plans tangents
Intuitivement, il semble clair que, dans un plan, une seule ligne peut être tangente à une courbe en un point. Cependant, dans un espace tridimensionnel, de nombreuses lignes peuvent être tangentes à un point donné. Si ces lignes se situent dans le même plan, elles déterminent le plan tangent à ce point. Une façon plus intuitive de concevoir un plan tangent est de supposer que la surface est lisse à ce point (pas de coins). Ainsi, une ligne tangente à la surface à ce point dans n'importe quelle direction ne présente aucun changement brusque de pente, car la direction change doucement. Par conséquent, dans un voisinage suffisamment restreint autour du point, un plan tangent ne touche la surface qu'à ce point.
\( P_0=(x_0,y_0,z_0)\)Soit un point sur une surface\( S\), et\( C\) soit n'importe quelle courbe qui la traverse\( P_0\) et se trouve entièrement dedans\( S\). Si les lignes tangentes à toutes ces courbes\( C\)\( P_0\) se situent dans le même plan, alors ce plan est appelé plan tangent à\( S\) at\( P_0\) (Figure\(\PageIndex{1}\)).

Pour qu'un plan tangent à une surface existe en un point de cette surface, il suffit que la fonction qui définit la surface soit différenciable à ce point. Nous définissons ici le terme plan tangent, puis nous explorons l'idée de manière intuitive.
\( S\)Soit une surface définie par une fonction dérivable\( z=f(x,y),\) et\( P_0=(x_0,y_0)\) soit un point dans le domaine de\( f\). Ensuite, l'équation du plan tangent à\( S\) at\( P_0\) est donnée par
\[z=f(x_0,y_0)+f_x(x_0,y_0)(x−x_0)+f_y(x_0,y_0)(y−y_0). \label{tanplane} \]
Pour comprendre pourquoi cette formule est correcte, trouvons d'abord deux lignes tangentes à la surface\( S\). L'équation de la tangente à la courbe qui est représentée par l'intersection de\( S\) avec la trace verticale donnée par\( x=x_0\) est\( z=f(x_0,y_0)+f_y(x_0,y_0)(y−y_0)\). De même, l'équation de la tangente à la courbe qui est représentée par l'intersection de\( S\) avec la trace verticale donnée par\( y=y_0\) est\( z=f(x_0,y_0)+f_x(x_0,y_0)(x−x_0)\). Un vecteur parallèle à la première ligne tangente est\( \vecs a=\,\hat{\mathbf j}+f_y(x_0,y_0)\,\hat{\mathbf k}\) ; un vecteur parallèle à la seconde ligne tangente l'est\(\vecs b=\hat{\mathbf i}+f_x(x_0,y_0)\,\hat{\mathbf k}\). Nous pouvons prendre le produit croisé de ces deux vecteurs :
\[\begin{align*} \vecs a\times \vecs b &=(\,\hat{\mathbf j}+f_y(x_0,y_0)\,\hat{\mathbf k})×(\,\hat{\mathbf i}+f_x(x_0,y_0)\,\hat{\mathbf k})\\[4pt] &=\begin{vmatrix}\hat{\mathbf i} & \hat{\mathbf j} & \hat{\mathbf k}\\[4pt] 0 & 1 & f_y(x_0,y_0)\\[4pt] 1 & 0 & f_x(x_0,y_0)\end{vmatrix} \\[4pt] &=f_x(x_0,y_0)\,\hat{\mathbf i}+f_y(x_0,y_0)\,\hat{\mathbf j}−\,\hat{\mathbf k}. \end{align*}\]
Ce vecteur est perpendiculaire aux deux lignes et est donc perpendiculaire au plan tangent. Nous pouvons utiliser ce vecteur comme vecteur normal au plan tangent, avec le point de\( P_0=(x_0,y_0,f(x_0,y_0))\) l'équation d'un plan :
\[ \begin{align*}\vecs n·((x−x_0)\,\hat{\mathbf i}+(y−y_0)\,\hat{\mathbf j}+(z−f(x_0,y_0))\,\hat{\mathbf k}) &=0 \\[4pt] (f_x(x_0,y_0)\,\hat{\mathbf i}+f_y(x_0,y_0)\,\hat{\mathbf j}-\,\hat{\mathbf k})·((x−x_0)\,\hat{\mathbf i}+(y−y_0)\,\hat{\mathbf j}+(z−f(x_0,y_0))\,\hat{\mathbf k}) &=0 \\[4pt] f_x(x_0,y_0)(x−x_0)+f_y(x_0,y_0)(y−y_0)−(z−f(x_0,y_0)) &=0. \end{align*}\]
La résolution de cette équation pour\(z\) donne l'équation \ ref {tanplane}.
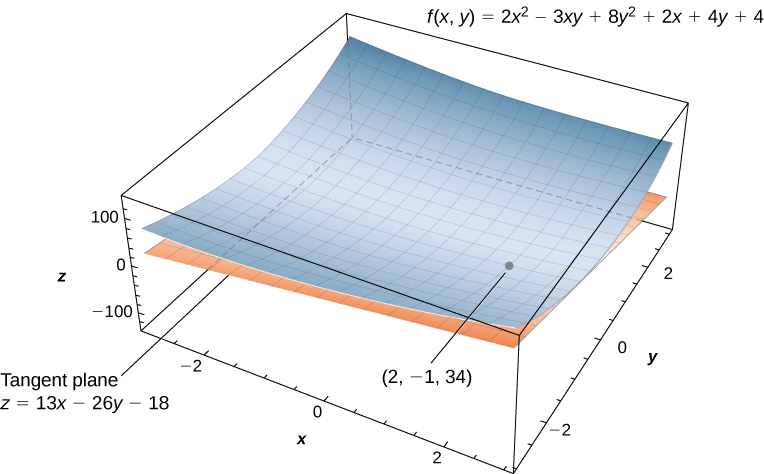
Trouvez l'équation du plan tangent à la surface définie par la fonction\( f(x,y)=2x^2−3xy+8y^2+2x−4y+4\) au point\( (2,−1).\)
Solution
Tout d'abord, nous devons calculer\( f_x(x,y)\) puis\( f_y(x,y)\) utiliser l'équation avec\( x_0=2\) et\( y_0=−1\) :
\[\begin{align*} f_x(x,y) &=4x−3y+2 \\[4pt] f_y(x,y) &=−3x+16y−4 \\[4pt] f(2,−1) &=2(2)^2−3(2)(−1)+8(−1)^2+2(2)−4(−1)+4=34 \\[4pt] f_x(2,−1) &=4(2)−3(−1)+2=13 \\[4pt] f_y(2,−1) &=−3(2)+16(−1)−4=−26.\end{align*}\]
Alors l'équation \ ref {tanplane} devient
\[\begin{align*} z &=f(x_0,y_0)+f_x(x_0,y_0)(x−x_0)+f_y(x_0,y_0)(y−y_0) \\[4pt] z &=34+13(x−2)−26(y−(−1)) \\[4pt] z &=34+13x−26−26y−26 \\[4pt] z &=13x−26y−18. \end{align*}\]
(Voir la figure suivante).
Trouvez l'équation du plan tangent à la surface définie par la fonction\( f(x,y)=x^3−x^2y+y^2−2x+3y−2\) au point\( (−1,3)\).
- Allusion
-
Commencez par calculer\( f_x(x,y)\) puis\( f_y(x,y)\) utilisez l'équation \ ref {tanplane}.
- Réponse
-
\( z=7x+8y−3\)
Trouvez l'équation du plan tangent à la surface définie par la fonction\( f(x,y)=\sin(2x)\cos(3y)\) au point\( (π/3,π/4).\)
Solution
Tout d'abord, calculez\( f_x(x,y)\) puis\( f_y(x,y)\) utilisez l'équation \ ref {tanplane} avec\( x_0=π/3\) et\( y_0=π/4\) :
\[\begin{align*} f_x(x,y) &=2\cos(2x)\cos(3y) \\[4pt] f_y(x,y) &=−3\sin(2x)\sin(3y) \\[4pt] f\left(\dfrac{π}{3},\dfrac{π}{4}\right) &=\sin\left(2\left(\dfrac{π}{3}\right)\right)\cos\left(3\left(\dfrac{π}{4}\right)\right)=\left(\dfrac{\sqrt{3}}{2}\right)\left(−\dfrac{\sqrt{2}}{2}\right)=−\dfrac{\sqrt{6}}{4} \\[4pt] f_x\left(\dfrac{π}{3},\dfrac{π}{4}\right) &=2\cos\left(2\left(\dfrac{π}{3}\right)\right)\cos\left(3\left(\dfrac{π}{4}\right)\right)=2\left(−\dfrac{1}{2}\right)\left(−\dfrac{\sqrt{2}}{2}\right)=\dfrac{\sqrt{2}}{2} \\[4pt] f_y \left(\dfrac{π}{3},\dfrac{π}{4}\right) &=−3\sin\left(2\left(\dfrac{π}{3}\right)\right)\sin\left(3\left(\dfrac{π}{4}\right)\right)=−3\left(\dfrac{\sqrt{3}}{2}\right)\left(\dfrac{\sqrt{2}}{2}\right)=−\dfrac{3\sqrt{6}}{4}. \end{align*}\]
Alors l'équation \ ref {tanplane} devient
\[\begin{align*} z &=f(x_0,y_0)+f_x(x_0,y_0)(x−x_0)+f_y(x_0,y_0)(y−y_0) \\[4pt] &=−\dfrac{\sqrt{6}}{4}+\dfrac{\sqrt{2}}{2}\left(x−\dfrac{π}{3}\right)−\dfrac{3\sqrt{6}}{4}\left(y−\dfrac{π}{4}\right) \\[4pt] &=\dfrac{\sqrt{2}}{2}x−\dfrac{3\sqrt{6}}{4}y−\dfrac{\sqrt{6}}{4}−\dfrac{π\sqrt{2}}{6}+\dfrac{3π\sqrt{6}}{16} \end{align*}\]
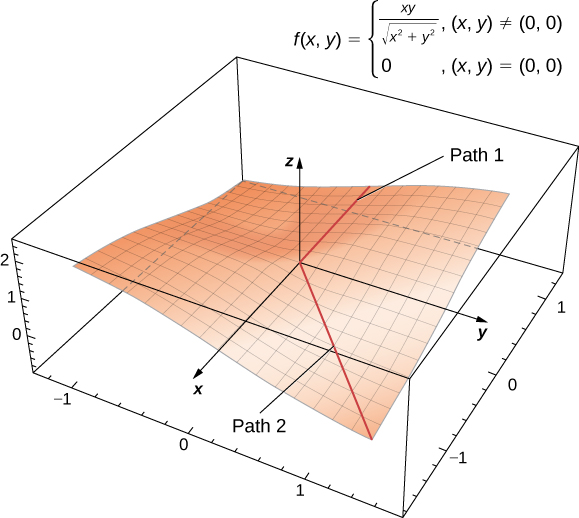
Un plan tangent à une surface n'existe pas toujours à chaque point de la surface. Considérez la fonction par morceaux
\[f(x,y)=\begin{cases}\dfrac{xy}{\sqrt{x^2+y^2}}, & & (x,y)≠(0,0)\\[4pt] 0, & & (x,y)=(0,0)\end{cases}. \label{oddfunction} \]
Le graphique de cette fonction est présenté ci-dessous.
Figure\(\PageIndex{3}\) : Graphique d'une fonction qui n'a pas de plan tangent à l'origine. Figure dynamique alimentée par CalcPlot3D.
Si l'\( x=0\)un ou l'autre\( f(x,y)=0,\) est\( y=0\), la valeur de la fonction ne change pas sur l'axe\(x\) \(y\)- ou -. Par conséquent\( f_x(x,0)=f_y(0,y)=0\), de manière à ce que l'\( y\)une\( x\) ou l'autre approche de zéro, ces dérivées partielles restent égales à zéro. En les remplaçant dans l'équation\( z=0\), on obtient l'équation de la tangente. Cependant, si nous abordons l'origine d'une manière différente, nous obtenons une histoire différente. Supposons, par exemple, que nous approchions l'origine le long de la ligne\( y=x\). Si nous insérons\( y=x\) dans la fonction d'origine, elle devient
\[f(x,x)=\dfrac{x(x)}{\sqrt{x^2+(x)^2}}=\dfrac{x^2}{\sqrt{2x^2}}=\dfrac{|x|}{\sqrt{2}}. \nonumber \]
Lorsque\( x>0,\) la pente de cette courbe est égale à\( \sqrt{2}/2\) ; lorsque\( x<0\), la pente de cette courbe est égale à\( −(\sqrt{2}/2).\) Cela pose un problème. Dans la définition du plan tangent, nous avons supposé que toutes les lignes tangentes passant par le point\( P\) (dans ce cas, l'origine) se trouvaient dans le même plan. Ce n'est clairement pas le cas en l'espèce. Lorsque nous étudions les fonctions dérivables, nous verrons que cette fonction n'est pas différenciable à l'origine.
Approximations linéaires
Rappelons à partir des approximations et des différentiels linéaires que la formule pour l'approximation linéaire d'une fonction\( f(x)\) au point\( x=a\) est donnée par
\[y≈f(a)+f'(a)(x−a). \nonumber \]
Le diagramme de l'approximation linéaire d'une fonction d'une variable apparaît dans le graphique suivant.
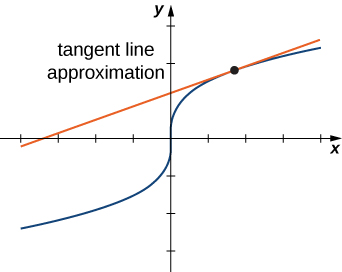
La droite tangente peut être utilisée comme approximation de la fonction\( f(x)\) pour des valeurs\( x\) raisonnablement proches de\( x=a\). Lorsque vous travaillez avec une fonction à deux variables, la droite tangente est remplacée par un plan tangent, mais l'idée de l'approximation est sensiblement la même.
Étant donné une fonction\( z=f(x,y)\) avec des dérivées partielles continues qui existent au point\( (x_0,y_0)\), l'approximation linéaire de\(f\) ce point\( (x_0,y_0)\) est donnée par l'équation
\[L(x,y)=f(x_0,y_0)+f_x(x_0,y_0)(x−x_0)+f_y(x_0,y_0)(y−y_0). \label{approx} \]
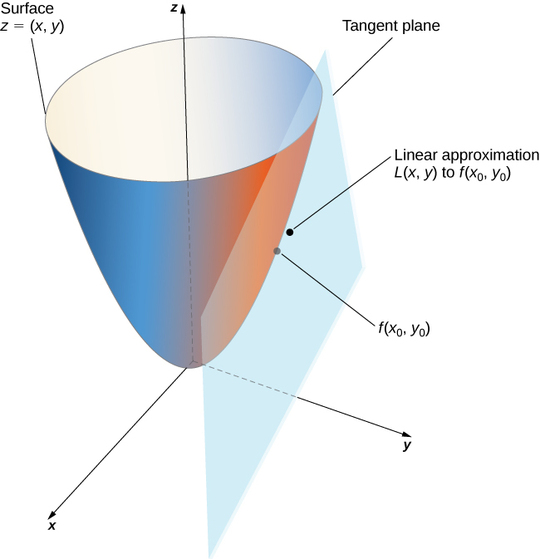
Notez que cette équation représente également le plan tangent à la surface définie par\( z=f(x,y)\) le point\( (x_0,y_0)\). L'idée qui sous-tend l'utilisation d'une approximation linéaire est que, s'il existe un point\( (x_0,y_0)\) auquel la valeur précise de\( f(x,y)\) est connue, alors pour des valeurs\( (x,y)\) raisonnablement proches\( (x_0,y_0)\), l'approximation linéaire (c'est-à-dire le plan tangent) produit une valeur qui est également raisonnablement proche de la valeur exacte de\( f(x,y)\) (Figure). De plus, le plan utilisé pour trouver l'approximation linéaire est également le plan tangent à la surface au point\( (x_0,y_0).\)
Compte tenu de la fonction\( f(x,y)=\sqrt{41−4x^2−y^2}\),\( f(2.1,2.9)\) approximez en utilisant un point\( (2,3)\) pour\( (x_0,y_0).\) Quelle est la valeur approximative de\( f(2.1,2.9)\) 1 à 4 décimales ?
Solution
Pour appliquer l'équation \ ref {approx}, nous devons d'abord calculer\( f(x_0,y_0), f_x(x_0,y_0),\) et\( f_y(x_0,y_0)\) utiliser\( x_0=2\) et\( y_0=3:\)
\[\begin{align*} f(x_0,y_0) &=f(2,3)=\sqrt{41−4(2)^2−(3)^2}=\sqrt{41−16−9}=\sqrt{16}=4 \\[4pt] f_x(x,y) &=−\dfrac{4x}{\sqrt{41−4x^2−y^2}} \text{ so} \; f_x(x_0,y_0)=−\dfrac{4(2)}{\sqrt{41−4(2)^2−(3)^2}}=−2 \\[4pt] f_y(x,y) &=−\dfrac{y}{\sqrt{41−4x^2−y^2}} \text{ so}\; f_y(x_0,y_0)=−\dfrac{3}{\sqrt{41−4(2)^2−(3)^2}}=−\dfrac{3}{4}. \end{align*}\]
Nous remplaçons maintenant ces valeurs dans l'équation \ ref {approx} :
\[\begin{align*} L(x,y) &=f(x_0,y_0)+f_x(x_0,y_0)(x−x_0)+f_y(x_0,y_0)(y−y_0) \\[4pt] &=4−2(x−2)−\dfrac{3}{4}(y−3) \\[4pt] &=\dfrac{41}{4}−2x−\dfrac{3}{4}y. \end{align*}\]
Enfin, nous remplaçons\( x=2.1\) et\( y=2.9\) introduisons\(L(x,y):\)
\[ L(2.1,2.9)=\dfrac{41}{4}−2(2.1)−\dfrac{3}{4}(2.9)=10.25−4.2−2.175=3.875. \nonumber \]
La valeur approximative comprise entre\( f(2.1,2.9)\) 1 et 4 décimales est
\[ f(2.1,2.9)=\sqrt{41−4(2.1)^2−(2.9)^2}=\sqrt{14.95}≈3.8665, \nonumber \]
ce qui correspond à une\( 0.2%\) erreur d'approximation.
Compte tenu de la fonction,\( f(4.1,0.9)\) utilisez\( f(x,y)=e^{5−2x+3y},\) approximativement le point\( (4,1)\) pour\( (x_0,y_0)\). Quelle est la valeur approximative comprise entre\( f(4.1,0.9)\) 1 et 4 décimales ?
- Allusion
-
Commencez par calculer\( f(x_0,y_0),f_x(x_0,y_0),\)\( x_0=4\) et\( f_y(x_0,y_0)\) utiliser\( y_0=1\), puis utilisez l'équation \ ref {approx}.
- Réponse
-
\( L(x,y)=6−2x+3y,\)donc\( L(4.1,0.9)=6−2(4.1)+3(0.9)=0.5\)\( f(4.1,0.9)=e^{5−2(4.1)+3(0.9)}=e^{−0.5}≈0.6065.\)
Différentiabilité
Lorsque vous travaillez avec une fonction\( y=f(x)\) d'une variable, la fonction est dite dérivable à un point\( x=a\) si\( f′(a)\) elle existe. De plus, si la fonction d'une variable est dérivable en un point, le graphe est « lisse » à ce point (c'est-à-dire qu'il n'existe aucun angle) et une ligne tangente est bien définie à ce point.
L'idée qui sous-tend la différentiabilité d'une fonction de deux variables est liée à l'idée de régularité à ce stade. Dans ce cas, une surface est considérée comme lisse à un point\( P\) si un plan tangent à la surface existe à ce point. Si une fonction est dérivable en un point, cela signifie qu'un plan tangent à la surface existe à ce point. Rappelez-vous que la formule (équation \ ref {tanplane}) pour un plan tangent en un point\( (x_0,y_0)\) est donnée par
\[z=f(x_0,y_0)+f_x(x_0,y_0)(x−x_0)+f_y(x_0,y_0)(y−y_0) \nonumber \]
Pour qu'un plan tangent existe au point\( (x_0,y_0),\), les dérivées partielles doivent donc exister à ce point. Cependant, cette condition n'est pas suffisante pour la douceur, comme l'illustre la figure. Dans ce cas, les dérivées partielles existaient à l'origine, mais la fonction avait également un coin sur le graphique à l'origine.
Une fonction\( f(x,y)\) est dérivable à un point\( P(x_0,y_0)\) si, pour tous les points\( (x,y)\) d'un\( δ\) disque environnant\( P\), on peut écrire
\[f(x,y)=f(x_0,y_0)+f_x(x_0,y_0)(x−x_0)+f_y(x_0,y_0)(y−y_0)+E(x,y), \label{diff1} \]
où le terme d'erreur\( E\) satisfait
\[\lim_{(x,y)→(x_0,y_0)}\dfrac{E(x,y)}{\sqrt{(x−x_0)^2+(y−y_0)^2}}=0. \label{diff2} \]
Le dernier terme de l'équation \ ref {diff1} est to comme terme d'erreur et il représente la proximité entre le plan tangent et la surface dans un petit voisinage (\( δ\)disque) d'un point\( P\). Pour que la fonction\( f\) soit dérivable en\( P\), elle doit être lisse, c'est-à-dire que le graphe de\( f\) doit être proche du plan tangent pour les points proches\( P\).
Afficher que la fonction\( f(x,y)=2x^2−4y\) est dérivable au point\( (2,−3).\)
Solution
Tout d'abord, nous calculons\( f(x_0,y_0),f_x(x_0,y_0),\)\( x_0=2\) et\( f_y(x_0,y_0)\) utilisons\( y_0=−3,\), puis nous utilisons l'équation \ ref {diff1} :
\[\begin{align*} f(2,−3) &=2(2)^2−4(−3)=8+12=20 \\[4pt] f_x(2,−3) &=4(2)=8 \\[4pt] f_y(2,−3) &=−4. \end{align*}\]
Par conséquent,\( m_1=8\)\( m_2=−4,\) et et l'équation \ ref {diff1} devient
\[ \begin{align*} f(x,y) &=f(2,−3)+f_x(2,−3)(x−2)+f_y(2,−3)(y+3)+E(x,y) \\[4pt] 2x^2−4y &=20+8(x−2)−4(y+3)+E(x,y) \\[4pt] 2x^2−4y &=20+8x−16−4y−12+E(x,y) \\[4pt] 2x^2−4y &=8x−4y−8+E(x,y) \\[4pt] E(x,y) &=2x^2−8x+8. \end{align*}\]
Ensuite, nous calculons la limite dans l'équation \ ref {diff2} :
\ [\ begin {align*} \ lim_ {(x, y) → (x_0, y_0)} \ dfrac {E (x, y)} {\ sqrt {(x−x+0) ^2+ (y−y_0) ^2}} &= \ lim_ {(x, y) → (2, −3)} \ dfrac {2x^2−8xx+8} {\ sqrt {(x−2) ^2+ (y+3) ^2}} \ \ [4 points]
&= \ lim_ {(x, y) → (2, −3)} \ dfrac {2 (x^2−4x+4)} {\ sqrt {(x−2) ^2+ (y+3) ^2}} \ \ [4 points]
&= lim_ {(x, y) → (2, −3)} \ dfrac {2 (x−2) ^2} {\ sqrt {(x −2) ^2+ (y+3) ^2}} \ \ [4 points]
&= \ lim_ {(x, y) → (2, −3)} \ dfrac {2 (x−2) ^2+ (y+3) ^2)} {\ sqrt {(x−2) ^2+ (y+3) ^2}} \ \ [4 points]
&= \ lim_ {(x, y) → (2, −3)} 2 \ sqrt {(x−2) ^2+ (y+3) ^2} \ \ [4 points]
&=0. \ end {align*} \]
Puisque\( E(x,y)≥0\) pour toute valeur de\( x\) ou\( y\), la limite initiale doit être égale à zéro. Par conséquent,\( f(x,y)=2x^2−4y\) est différenciable au point\( (2,−3)\).
Montrez que la fonction\( f(x,y)=3x−4y^2\) est dérivable au point\((−1,2)\).
- Allusion
-
Tout d'abord, calculez\( f(x_0,y_0),f_x(x_0,y_0),\)\( x_0=−1\) et\( f_y(x_0,y_0)\) utilisez\( y_0=2\), puis utilisez l'équation \ ref {diff2} pour trouver\( E(x,y)\). Enfin, calculez la limite.
- Réponse
-
\ [\ begin {align*} f (−1,2) &=−19, \ quad f_x (−1,2) =3, \ quad f_y (−1,2) =−16, \ quad E (x, y) =−4 (y−2) ^2. \ \ [4 points]
\ lim_ {(x, y) → (x_0, y_0)} \ dfrac {E (E) x, y)} {\ sqrt {(x−x_0) ^2+ (y−y_0) ^2}} &= \ lim_ {(x, y) → (−1,2)} \ dfrac {−4 (y−2) ^2} {\ sqrt {(x+1) ^2+ (y−2) ^2}} \ \ [4 points]
&≤ \ lim_ {(x, y) → (−1,2)} \ dfrac {−4 (x+1) ^2+ (y−2) ^2)} {\ sqrt {(x+1) ^2+ (y−2) ^2}} \ \ [4 points]
&= \ lim_ {(x, y) → (2, −3)} −4 \ sqrt {(x+1) ^2+ (y−2) ^2} \ \ [4 points]
&=0. \ end {align*} \]
Cette fonction provient de (Equation \ ref {oddfunction})
\[ f(x,y)=\begin{cases}\dfrac{xy}{\sqrt{x^2+y^2}}, & & (x,y)≠(0,0)\\[4pt] 0, & & (x,y)=(0,0)\end{cases} \nonumber \]
n'est pas différenciable à l'origine (Figure\(\PageIndex{3}\)). Nous pouvons le constater en calculant les dérivées partielles. Cette fonction est apparue plus tôt dans la section, où nous l'avons montrée\( f_x(0,0)=f_y(0,0)=0\). En substituant ces informations dans les équations \ ref {diff1} et \ ref {diff2} en utilisant\( x_0=0\) et\( y_0=0\), nous obtenons
\[\begin{align*} f(x,y) &=f(0,0)+f_x(0,0)(x−0)+f_y(0,0)(y−0)+E(x,y) \\[4pt] E(x,y) &=\dfrac{xy}{\sqrt{x^2+y^2}}. \end{align*}\]
Calculer
\[ \lim_{(x,y)→(x_0,y_0)}\dfrac{E(x,y)}{\sqrt{(x−x_0)^2+(y−y_0)^2}} \nonumber \]
donne
\[\begin{align*} \lim_{(x,y)→(x_0,y_0)}\dfrac{E(x,y)}{\sqrt{(x−x_0)^2+(y−y_0)^2}} &=\lim_{(x,y)→(0,0)}\dfrac{\dfrac{xy}{\sqrt{x^2+y^2}}}{\sqrt{x^2+y^2}} \\[4pt] &=\lim_{(x,y)→(0,0)}\dfrac{xy}{x^2+y^2}. \end{align*}\]
Selon le chemin emprunté vers l'origine, cette limite prend des valeurs différentes. Par conséquent, la limite n'existe pas et la fonction n'\( f\)est pas différenciable à l'origine, comme le montre la figure suivante.
La dérivabilité et la continuité des fonctions de deux variables ou plus sont liées, de la même manière que pour les fonctions d'une variable. En fait, avec quelques ajustements de notation, le théorème de base est le même.
\( z=f(x,y)\)Soit une fonction de deux variables ayant\( (x_0,y_0)\) dans le domaine de\( f\). Si\( f(x,y)\) est différenciable à\( (x_0,y_0)\), alors\( f(x,y)\) est continu à\( (x_0,y_0).\)
La note montre que si une fonction est dérivable en un point, elle y est continue. Toutefois, si une fonction est continue à un point, elle n'est pas nécessairement dérivable à ce point. Par exemple, la fonction décrite ci-dessus (Equation \ ref {oddfunction})
\[f(x,y)=\begin{cases}\dfrac{xy}{\sqrt{x^2+y^2}}, & & (x,y)≠(0,0)\\[4pt] 0, & & (x,y)=(0,0)\end{cases} \nonumber \]
est continu à l'origine, mais il n'est pas différenciable à l'origine. Cette observation est également similaire à la situation du calcul à variable unique.
Nous pouvons explorer plus en détail le lien entre continuité et différentiabilité à un moment donné. Le théorème suivant indique que si la fonction et ses dérivées partielles sont continues en un point, la fonction est dérivable.
\( z=f(x,y)\)Soit une fonction de deux variables ayant\( (x_0,y_0)\) dans le domaine de\( f\). Si\(f(x,y)\)\(f_x(x,y)\), et si\(f_y(x,y)\) tous existent dans un voisinage de\((x_0,y_0)\) et sont continus à\((x_0,y_0)\), alors\(f(x,y)\) ils y sont différenciables.
Rappelons que nous avons montré précédemment que la fonction dans Equation \ ref {oddfunction} n'était pas dérivable à l'origine. Calculons les dérivées partielles\( f_x\) et\( f_y\) :
\[ \dfrac{∂f}{∂x}=\dfrac{y^3}{(x^2+y^2)^{3/2}} \nonumber \]
et
\[\dfrac{∂f}{∂y}=\dfrac{x^3}{(x^2+y^2)^{3/2}}. \nonumber \]
La contre-hypothèse du théorème précédent indique que si une fonction n'est pas dérivable, alors au moins l'une des hypothèses doit être fausse. Explorons la condition qui\( f_x(0,0)\) doit être continue. Pour que cela soit vrai, il doit être vrai que
\[ \lim_{(x,y)→(0,0)} f_x(x,y)=f_x(0,0) \nonumber \]
donc
\[ \lim_{(x,y)→(0,0)}f_x(x,y)=\lim_{(x,y)→(0,0)}\dfrac{y^3}{(x^2+y^2)^{3/2}}. \nonumber \]
Laissez\( x=ky\). Alors
\ [\ begin {align*} \ lim_ {(x, y) → (0,0)} \ dfrac {y^3} {(x^2+y^2) ^ {3/2}} &= \ lim_ {y→0} \ dfrac {y^3} {((ky) ^2+y^2) ^ {3/2}} \ \ [4 points]
&= \ lim_ {y→0} \ dfrac {y^3} {(k^2y^2+y^2) ^ {3/2}} \ \ [4 points] &= \ lim_ {y→0} \ dfrac {y^3} {|y|^3 (k^2+1) ^ {3/2}} \ \ [4 points]
&= \ dfrac {1} {(k^2+1) ^ {3/2}} \ \ [4 points]
&= \ dfrac {1} {(k^2+1) ^ {3/2}} \ \ [4 points] 2+1) ^ {3/2}} \ lim_ {y →0} \ frac {|y|} {y}. \ end {align*} \]
Si\( y>0\), alors cette expression est égale\( 1/(k^2+1)^{3/2}\) ; si\( y<0\), alors elle est égale à\( −(1/(k^2+1)^{3/2})\). Dans les deux cas, la valeur dépend de\( k\), de sorte que la limite n'existe pas.
Différentiels
Dans Approximations et différentiels linéaires, nous avons d'abord étudié le concept de différentiels. Le différentiel de\( y\), écrit\( dy\), est défini comme\( f′(x)dx\). Le différentiel est utilisé pour approximer\( Δy=f(x+Δx)−f(x)\), où\( Δx=dx\). En étendant cette idée à l'approximation linéaire d'une fonction de deux variables au point,\( (x_0,y_0)\) on obtient la formule du différentiel total pour une fonction de deux variables.
\( z=f(x,y)\)Soit une fonction de deux variables ayant\( (x_0,y_0)\) dans le domaine de\( f\),\( Δx\) et\( Δy\) soit choisie de telle sorte qu'elle\( (x_0+Δx,y_0+Δy)\) soit également dans le domaine de\( f\). Si\( f\) est dérivable au point\( (x_0,y_0)\), alors les différentiels\( dx\) et\( dy\) sont définis comme
\[dx=Δx \nonumber \]
et
\[dy=Δy. \nonumber \]
Le différentiel\( dz\), également appelé différentiel total de\( z=f(x,y)\) at\( (x_0,y_0)\), est défini comme
\[dz=f_x(x_0,y_0)dx+f_y(x_0,y_0)dy. \label{total} \]
Notez que le symbole n'\( ∂\)est pas utilisé pour indiquer le différentiel total ; il\( d\) apparaît plutôt devant\( z\). Maintenant, définissons\( Δz=f(x+Δx,y+Δy)−f(x,y).\) que nous utilisons\( dz\) pour approximer\( Δz\), donc
\[Δz≈dz=f_x(x_0,y_0)dx+f_y(x_0,y_0)dy. \nonumber \]
Par conséquent, le différentiel est utilisé pour approximer la variation de la fonction\( z=f(x_0,y_0)\) au point\( (x_0,y_0)\) pour des valeurs données de\( Δx\) et\( Δy\). Puisque\( Δz=f(x+Δx,y+Δy)−f(x,y)\), cela peut être utilisé davantage pour approximer\( f(x+Δx,y+Δy):\)
\[ f(x+Δx,y+Δy)=f(x,y)+Δz≈f(x,y)+fx(x_0,y_0)Δx+f_y(x_0,y_0)Δy. \nonumber \]
Reportez-vous à la figure suivante.

L'une des applications de cette idée consiste à déterminer la propagation des erreurs. Par exemple, si nous fabriquons un gadget et que nous sommes en retard dans la mesure d'une quantité donnée, le différentiel peut être utilisé pour estimer l'erreur dans le volume total du gadget.
Trouvez le différentiel\( dz\) de la fonction\( f(x,y)=3x^2−2xy+y^2\) et utilisez-le pour obtenir une approximation\( Δz\) au point\( (2,−3).\) Use\( Δx=0.1\) et à\( Δy=−0.05.\) quelle est la valeur exacte de\( Δz\) ?
Solution
Tout d'abord, nous devons calculer\( f(x_0,y_0),f_x(x_0,y_0),\)\( x_0=2\) et\( f_y(x_0,y_0)\) utiliser\( y_0=−3:\)
\[\begin{align*} f(x_0,y_0) &=f(2,−3)=3(2)^2−2(2)(−3)+(−3)^2=12+12+9=33 \\[4pt] f_x(x,y) &=6x−2y \\[10pt] f_y(x,y) &=−2x+2y \\[4pt] f_x(x_0,y_0) &= fx(2,−3) \\[4pt] &=6(2)−2(−3)=12+6=18 \\[10pt] f_y(x_0,y_0) &=f_y(2,−3) \\[4pt] &=−2(2)+2(−3) \\[4pt] &=−4−6=−10. \end{align*}\]
Ensuite, nous substituons ces quantités dans l'équation \ ref {total} :
\[\begin{align*} dz &=f_x(x_0,y_0)dx+f_y(x_0,y_0)dy \\[4pt] dz &=18(0.1)−10(−0.05)=1.8+0.5=2.3. \end{align*}\]
Il s'agit de l'approximation de\( Δz=f(x_0+Δx,y_0+Δy)−f(x_0,y_0).\) La valeur exacte de\( Δz\) est donnée par
\[\begin{align*} Δz &=f(x_0+Δx,y_0+Δy)−f(x_0,y_0) \\[4pt] &=f(2+0.1,−3−0.05)−f(2,−3) \\[4pt] &=f(2.1,−3.05)−f(2,−3) \\[4pt] &=2.3425. \end{align*}\]
Trouvez le différentiel\( dz\) de la fonction\( f(x,y)=4y^2+x^2y−2xy\) et utilisez-le pour obtenir une approximation\( Δz\) au point\( (1,−1)\). Utilisez\( Δx=0.03\) et\( Δy=−0.02\). Quelle est la valeur exacte de\( Δz\) ?
- Allusion
-
Tout d'abord, calculez\( f_x(x_0,y_0)\)\( x_0=1\) et\( f_y(x_0,y_0)\) utilisez\( y_0=−1\), puis utilisez l'équation \ ref {total}.
- Réponse
-
\( dz=0.18\)
\( Δz=f(1.03,−1.02)−f(1,−1)=0.180682\)
Différentiabilité d'une fonction à trois variables
Tous les résultats précédents concernant la différentiabilité des fonctions de deux variables peuvent être généralisés aux fonctions de trois variables. Tout d'abord, la définition :
Une fonction\( f(x,y,z)\) est dérivable à un point\( P(x_0,y_0,z_0)\) si, pour tous les points\( (x,y,z)\) d'un\( δ\) disque environnant,\( P\) nous pouvons écrire
\[f(x,y)=f(x_0,y_0,z_0)+f_x(x_0,y_0,z_0)(x−x_0)+f_y(x_0,y_0,z_0)(y−y_0)+f_z(x_0,y_0,z_0)(z−z_0)+E(x,y,z), \nonumber \]
où le terme d'erreur E satisfait
\[\lim_{(x,y,z)→(x_0,y_0,z_0)}\dfrac{E(x,y,z)}{\sqrt{(x−x_0)^2+(y−y_0)^2+(z−z_0)^2}}=0. \nonumber \]
Si une fonction de trois variables est dérivable en un point\( (x_0,y_0,z_0)\), elle y est continue. De plus, la continuité des premières dérivées partielles à ce stade garantit la différentiabilité.
Concepts clés
- L'analogue d'une droite tangente à une courbe est un plan tangent à une surface pour les fonctions de deux variables.
- Les plans tangents peuvent être utilisés pour approximer des valeurs de fonctions proches de valeurs connues.
- Une fonction est dérivable à un point si elle est « lisse » à ce point (c'est-à-dire qu'il n'y a pas de coins ou de discontinuités à ce point).
- Le différentiel total peut être utilisé pour approximer la variation d'une fonction\( z=f(x_0,y_0)\) au point\( (x_0,y_0)\) pour des valeurs données de\( Δx\) et\( Δy\).
Équations clés
- Plan tangent
\( z=f(x_0,y_0)+f_x(x_0,y_0)(x−x_0)+f_y(x_0,y_0)(y−y_0)\)
- Approximation linéaire
\( L(x,y)=f(x_0,y_0)+f_x(x_0,y_0)(x−x_0)+f_y(x_0,y_0)(y−y_0)\)
- Différentiel total
\( dz=f_x(x_0,y_0)dx+f_y(x_0,y_0)dy\).
- Différentiabilité (deux variables)
\( f(x,y)=f(x_0,y_0)+f_x(x_0,y_0)(x−x_0)+f_y(x_0,y_0)(y−y_0)+E(x,y),\)
où le terme d'erreur\( E\) satisfait
\(\displaystyle \lim_{(x,y)→(x_0,y_0)}\dfrac{E(x,y)}{\sqrt{(x−x_0)^2+(y−y_0)^2}}=0\).
- Différentiabilité (trois variables)
\( f(x,y)=f(x_0,y_0,z_0)+f_x(x_0,y_0,z_0)(x−x_0)+f_y(x_0,y_0,z_0)(y−y_0)+f_z(x_0,y_0,z_0)(z−z_0)+E(x,y,z),\)
où le terme d'erreur\( E\) satisfait
\(\displaystyle \lim_{(x,y,z)→(x_0,y_0,z_0)}\dfrac{E(x,y,z)}{\sqrt{(x−x_0)^2+(y−y_0)^2+(z−z_0)^2}}=0\).
Lexique
- différenciable
-
une fonction\( f(x,y)\) est dérivable\( (x_0,y_0)\) si elle\( f(x,y)\) peut être exprimée sous la forme\( f(x,y)=f(x_0,y_0)+f_x(x_0,y_0)(x−x_0)+f_y(x_0,y_0)(y−y_0)+E(x,y),\)
où le terme d'erreur\( E(x,y)\) satisfait\( \lim_{(x,y)→(x_0,y_0)}\dfrac{E(x,y)}{\sqrt{(x−x_0)^2+(y−y_0)^2}}=0\)
- approximation linéaire
- étant donné une fonction\( f(x,y)\) et un plan tangent à la fonction en un point\( (x_0,y_0)\), nous pouvons approximer\( f(x,y)\) les points proches\( (x_0,y_0)\) en utilisant la formule du plan tangent
- plan tangent
- étant donné une fonction\( f(x,y)\) dérivable en un point\( (x_0,y_0)\), l'équation du plan tangent à la surface\( z=f(x,y)\) est donnée par\( z=f(x_0,y_0)+f_x(x_0,y_0)(x−x_0)+f_y(x_0,y_0)(y−y_0)\)
- différentiel total
- le différentiel total de la fonction\( f(x,y)\) at\( (x_0,y_0)\) est donné par la formule\( dz=f_x(x_0,y_0)dx+fy(x_0,y_0)dy\)


