14.3E : Exercices pour la section 14.3

Last updated
Save as PDF

Page ID: 197387

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Dans l'exercice suivant, calculez la dérivée partielle en utilisant uniquement les définitions des limites.

1)$\dfrac{∂z}{∂y}$ pour$ z=x^2−3xy+y^2$

Réponse: $\dfrac{∂z}{∂y}=−3x+2y$

Pour les exercices 2 à 5, calculez le signe de la dérivée partielle à l'aide du graphique de la surface.

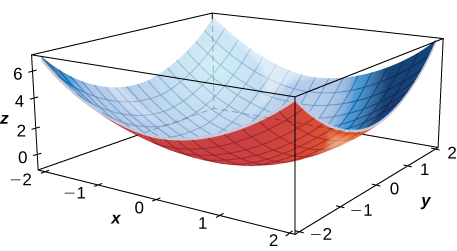
$Diagramme de surface d'un paraboloïde concave vers le haut et dont le sommet est à l'origine$

2)$ f_x(1,1)$

3)$ f_x(−1,1)$

Réponse: Le signe est négatif.

4)$ f_y(1,1)$

5)$ f_x(0,0)$

Réponse: La dérivée partielle est nulle à l'origine.

Dans les exercices 6 à 16, calculez les dérivées partielles demandées.

6)$ \dfrac{∂z}{∂x}$ pour$ z=\sin(3x)\cos(3y)$

7)$ \dfrac{∂z}{∂y}$ pour$ z=\sin(3x)\cos(3y)$

Réponse: $ \dfrac{∂z}{∂y}=−3\sin(3x)\sin(3y)$

8)$ \dfrac{∂z}{∂x}$ et$ \dfrac{∂z}{∂y}$ pour$ z=x^8e^3y$

9)$ \dfrac{∂z}{∂x}$ et$ \dfrac{∂z}{∂y}$ pour$ z=\ln(x^6+y^4)$

Réponse: $ \dfrac{∂z}{∂x}=\frac{6x^5}{x^6+y^4};\quad \dfrac{∂z}{∂y}=\frac{4y^3}{x^6+y^4}$

10) Rechercher$ f_y(x,y)$ pour$ f(x,y)=e^{xy}\cos(x)\sin(y).$

11) Laissez$ z=e^{xy}.$ trouver$ \dfrac{∂z}{∂x}$ et$ \dfrac{∂z}{∂y}$.

Réponse: $ \dfrac{∂z}{∂x}=ye^{xy};\quad \dfrac{∂z}{∂y}=xe^{xy}$

12) Laissez$ z=\ln(\frac{x}{y})$. Trouvez$ \dfrac{∂z}{∂x}$ et$ \dfrac{∂z}{∂y}$.

13) Laissez$ z=\tan(2x−y).$ trouver$ \dfrac{∂z}{∂x}$ et$ \dfrac{∂z}{∂y}$.

Réponse: $ \dfrac{∂z}{∂x}=2\sec^2(2x−y),\quad \dfrac{∂z}{∂y}=−\sec^2(2x−y)$

14) Laissez$ z=\sinh(2x+3y).$ trouver$ \dfrac{∂z}{∂x}$ et$ \dfrac{∂z}{∂y}$.

15) Laissez$ f(x,y)=\arctan(\frac{y}{x}).$ évaluer$ f_x(2,−2)$ et$ f_y(2,−2)$.

Réponse: $ f_x(2,−2)=\frac{1}{4}=f_y(2,−2)$

16) Laissons$ f(x,y)=\dfrac{xy}{x−y}.$ trouver$ f_x(2,−2)$ et$ f_y(2,−2).$

17) Trouvez$ \dfrac{∂z}{∂x}$$ (0,1)$ pour$ z=e^{−x}cos(y)$.

Réponse: $ \dfrac{∂z}{∂x}=−\cos(1)$

18) Compte tenu de la$ f(x,y,z)=x^3yz^2,$ découverte$ \dfrac{∂^2f}{∂x∂y}$ et$ f_z(1,1,1).$

19) Étant donné$ f_x(0,\frac{π}{2},−4)$ la$ f(x,y,z)=2\sin(x+y),$ découverte$f_y(0,\frac{π}{2},−4)$, et$ f_z(0,\frac{π}{2},−4)$.

Réponse: $ f_x(x,y,z)=0,\quad f_y(x,y,z)=0,\quad f_z(x,y,z)=0$

20) L'aire d'un parallélogramme dont les longueurs des côtés adjacents sont$ a$ et$ b$, et dans laquelle se situe l'angle entre ces deux côtés$ θ$, est donnée par la fonction$ A(a,b,θ)=ba\sin(θ).$ Trouver le taux de variation de l'aire du parallélogramme par rapport à ce qui suit :

a. Côté$a$

b. Côté$b$

c. Angle$θ$

21) Exprimer le volume d'un cylindre circulaire droit en fonction de deux variables :

a. son rayon$ r$ et sa hauteur$ h$.

b. Montrez que le taux de variation du volume du cylindre par rapport à son rayon est le produit de sa circonférence multiplié par sa hauteur.

c. Montrez que la vitesse de variation du volume du cylindre par rapport à sa hauteur est égale à l'aire de la base circulaire.

Réponse: $ a. V(r,h)=πr^2h$
$ b. \dfrac{∂V}{∂r}=2πrh$
$ c. \dfrac{∂V}{∂h}=πr^2$

22) Calculez$ \dfrac{∂w}{∂z}$ pour$ w=z\sin(xy^2+2z).$

Dans les exercices 23 à 39, trouvez les dérivées partielles d'ordre supérieur indiquées.

23)$ f_{xy}(x,y)$ pour$ f(x,y)=\ln(x−y)$

Réponse: $ f_{xy}(x,y)=\frac{1}{(x−y)^2}$

24)$ f_{yx}(x,y)$ pour$ f(x, y)=\ln(x−y)$

25) Let$ z=x^2+3xy+2y^2.$ Find$ \dfrac{∂^2z}{∂x^2}$ et$ \dfrac{∂^2z}{∂y^2}$.

Réponse: $ \dfrac{∂^2z}{∂x^2}=2,\quad \dfrac{∂^2z}{∂y^2}=4$

26) Étant donné$ z=e^x\tan y$, trouvez$ \dfrac{∂^2z}{∂x∂y}$ et$ \dfrac{∂^2z}{∂y∂x}$.

27) Étant donné la$ f(x,y,z)=xyz,$ découverte$ f_{xyy}(x,y,z),\, f_{yxy}(x,y,z),$ et$ f_{yyx}(x,y,z)$.

Réponse: $ f_{xyy}(x,y,z)=f_{yxy}(x,y,z)=f_{yyx}(x,y,z)=0$

28) Étant donné,$ f(x,y,z)=e^{−2x}\sin(z^2y),$ montrez que$ f_{xyy}(x,y,z)=f_{yxy}(x,y,z)$.

29) Montrez que$ z=\frac{1}{2}(e^y−e^{−y})\sin x$ c'est une solution de l'équation différentielle$ \dfrac{∂^2z}{∂x^2}+\dfrac{∂^2z}{∂y^2}=0.$

Réponse: $ \dfrac{d^2z}{dx^2}=−\frac{1}{2}(e^y−e^{−y})\sin x$
$ \dfrac{d^2z}{dy^2}=\frac{1}{2}(e^y−e^{−y})\sin x$
$ \dfrac{d^2z}{dx^2}+\dfrac{d^2z}{dy^2}=0$

30) Trouvez$ f_{xx}(x,y)$ pour$ f(x,y)=\frac{4x^2}{y}+\frac{y^2}{2x}.$

31) Laissons$ f(x,y,z)=x^2y^3z−3xy^2z^3+5x^2z−y^3z.$ trouver$ f_{xyz}.$

Réponse: $ f_{xyz}(x,y,z)=6y^2x−18yz^2$

32) Laissons$ F(x,y,z)=x^3yz^2−2x^2yz+3xz−2y^3z.$ trouver$ F_{xyz}(x,y,z)$.

33) Étant donné,$ f(x,y)=x^2+x−3xy+y^3−5,$ trouvez tous les points auxquels$ f_x(x,y)=f_y(x,y)=0$ simultanément.

Réponse: $ (\frac{1}{4},\frac{1}{2}),\quad (1,1)$

34) Étant donné,$ f(x,y)=2x^2+2xy+y^2+2x−3,$ trouvez tous les points auxquels$ \dfrac{∂f}{∂x}=0$ et$ \dfrac{∂f}{∂y}=0$ simultanément.

35) Étant donné$ f(x,y)=y^3−3yx^2−3y^2−3x^2+1$, trouvez tous les points sur lesquels$ f$$ f_x(x, y)=f_y(x, y)=0$ simultanément.

Réponse: $ (0,0),\quad (0,2),\quad (\sqrt{3},−1), \quad (−\sqrt{3},−1)$

36) Étant donné,$ f(x,y)=15x^3−3xy+15y^3,$ trouvez tous les points auxquels$ f_x(x,y)=f_y(x,y)=0$ simultanément.

37) Afficher que cela$ z=e^x\sin y$ répond à l'équation$ \dfrac{∂^2z}{∂x^2}+\dfrac{∂^2z}{∂y^2}=0.$

Réponse: $ \dfrac{∂^2z}{∂x^2}+\dfrac{∂^2z}{∂y^2}=e^x\sin y−e^x\sin y=0$

38) Montre qui$ f(x,y)=\ln(x^2+y^2)$ résout l'équation de Laplace$ \dfrac{∂^2z}{∂x^2}+\dfrac{∂^2z}{∂y^2}=0.$

39) Afficher que cela$ z=e^{−t}\cos(\frac{x}{c})$ répond à l'équation de la chaleur$ \dfrac{∂z}{∂t}=−e^{−t}\cos(\frac{x}{c}).$

Réponse: $ c^2\dfrac{∂^2z}{∂x^2}=e^{−t}\cos(\frac{x}{c})$

40) Trouvez$\displaystyle \lim_{Δx→0}\frac{f(x+Δx)−f(x,y)}{Δx}$ pour$ f(x,y)=−7x−2xy+7y.$

41) Trouvez$\displaystyle \lim_{Δy→0}\frac{f(x,y+Δy)−f(x,y)}{Δy}$ pour$ f(x,y)=−7x−2xy+7y.$

Réponse: $ \dfrac{∂f}{∂y}=−2x+7$

42) Trouvez$\displaystyle \lim_{Δx→0}\frac{Δf}{Δx}=\lim_{Δx→0}\frac{f(x+Δx,y)−f(x,y)}{Δx}$ pour$ f(x,y)=x^2y^2+xy+y.$

43) Trouvez$\displaystyle \lim_{Δx→0}\frac{Δf}{Δx}=\lim_{Δx→0}\frac{f(x+Δx,y)−f(x,y)}{Δx}$ pour$ f(x,y)=\sin(xy).$

Réponse: $ \dfrac{∂f}{∂x}=y\cos xy$

44) La fonction$ P(T,V)=\dfrac{nRT}{V}$ donne la pression à un point dans un gaz en fonction de la température$ T$ et du volume$ V$. Les lettres$ n$ et$ R$ sont des constantes. Trouvez$ \dfrac{∂P}{∂V}$ et$ \dfrac{∂P}{∂T}$ expliquez ce que ces quantités représentent.

45) L'équation du flux de chaleur dans le$ xy$ plan est$ \dfrac{∂f}{∂t}=\dfrac{∂^2f}{∂x^2}+\dfrac{∂^2f}{∂y^2}$. Montrez que$ f(x,y,t)=e^{−2t}\sin x\sin y$ c'est une solution.

46) L'équation d'onde de base est$ f_{tt}=f_{xx}.$ Vérifiez cela$ f(x,t)=\sin(x+t)$ et$ f(x,t)=\sin(x−t)$ sont des solutions.

47) La loi des cosinus peut être considérée comme une fonction de trois variables. $ θ$Soit$ x,y,$ les deux côtés de n'importe quel triangle où l'angle$ θ$ est l'angle inclus entre les deux côtés. Ensuite,$ F(x,y,θ)=x^2+y^2−2xy\cos θ$ donne le carré du troisième côté du triangle. Trouvez$ \dfrac{∂F}{∂θ}$,$ \dfrac{∂F}{∂x}$ quand$ x=2,\,y=3,$ et$ θ=\frac{π}{6}.$

Réponse: $ \dfrac{∂F}{∂θ}=6,\quad \dfrac{∂F}{∂x}=4−3\sqrt{3}$

48) Supposons que les côtés d'un rectangle changent en fonction du temps. Le premier côté change à un rythme de$ 2$ l'intérieur. /sec alors que le second côté change à la vitesse de$ 4$ in/sec. À quelle vitesse la diagonale du rectangle change-t-elle lorsque le premier côté mesure$ 16$ dedans et que le second côté mesure$ 20$ dedans ? (La réponse est arrondie à trois décimales.)

49) Une fonction de production de Cobb-Douglas est l'$ f(x,y)=200x^{0.7}y^{0.3},$endroit$ x$ et la$ y$ représentation de la quantité de main-d'œuvre et de capital disponibles. $ x=500$Let et$ y=1000.$ Find$ \dfrac{∂f}{∂x}$ et$ \dfrac{∂f}{∂y}$ à ces valeurs, qui représentent la productivité marginale du travail et du capital, respectivement.

Réponse: $ \dfrac{∂f}{∂x}$$ (500,1000)=172.36, \quad \dfrac{∂f}{∂y}$à$ (500,1000)=36.93$

50) L'indice de température apparente est une mesure de la sensation de la température, et il est basé sur deux variables :$ h$, qui est l'humidité relative$ t$, et qui est la température de l'air.

$ A=0.885t−22.4h+1.20th−0.544.$Trouvez$ \dfrac{∂A}{∂t}$,$ \dfrac{∂A}{∂h}$ quand$ t=20°F$ et$ h=0.90.$