14.3 : Dérives partielles

Objectifs d'apprentissage

• Calculez les dérivées partielles d'une fonction de deux variables.
• Calculez les dérivées partielles d'une fonction de plus de deux variables.
• Déterminez les dérivées d'ordre supérieur d'une fonction de deux variables.
• Expliquez la signification d'une équation aux dérivées partielles et donnez un exemple.

Maintenant que nous avons examiné les limites et la continuité des fonctions de deux variables, nous pouvons procéder à l'étude des dérivées. Trouver des dérivées de fonctions de deux variables est le concept clé de ce chapitre, avec autant d'applications en mathématiques, en sciences et en génie que la différenciation de fonctions à variable unique. Cependant, nous avons déjà vu que les limites et la continuité des fonctions multivariables soulèvent de nouveaux problèmes et nécessitent une nouvelle terminologie et de nouvelles idées pour les résoudre. Cela se répercute également sur la différenciation.

Dérivées d'une fonction de deux variables

Lors de l'étude des dérivées des fonctions d'une variable, nous avons découvert qu'une interprétation de la dérivée est un taux de variation instantané de,\(y\) en fonction de la notation de\(x.\) Leibniz pour la dérivée est,\(dy/dx,\) ce qui implique que\(y\) c'est la variable dépendante et\(x\) est la variable indépendante. Pour une fonction\(z=f(x,y)\) de deux variables,\(x\) et\(y\) sont les variables indépendantes et\(z\) est la variable dépendante. Cela soulève deux questions d'emblée : comment adapter la notation Leibniz pour les fonctions de deux variables ? En outre, qu'est-ce qu'une interprétation de la dérivée ? La réponse se trouve dans les dérivées partielles.

Définition : dérivées partielles

\(f(x,y)\)Soyons une fonction de deux variables. Ensuite, la dérivée partielle de\(f\) par rapport à\(x\), écrite comme\(∂f/∂x,\), ou\(f_x,\) est définie comme

\[\dfrac{∂f}{∂x}=f_x(x,y)=\lim_{h→0}\dfrac{f(x+h,y)−f(x,y)}{h} \label{pd1} \]

La dérivée partielle de\(f\) par rapport à\(y\), écrite comme\(∂f/∂y\), ou\(f_y,\) est définie comme

\[\dfrac{∂f}{∂y}=f_y(x,y)=\lim_{k→0}\dfrac{f(x,y+k)−f(x,y)}{k}. \label{pd2} \]

Cette définition montre déjà deux différences. Tout d'abord, la notation change, dans le sens où nous utilisons toujours une version de la notation Leibniz, mais la\(d\) notation originale est remplacée par le symbole\(∂\). (Cet arrondi\(“d”\) est généralement appelé « partiel »,\(∂f/∂x\) c'est pourquoi on parle de « partiel\(f\) par rapport à »\(x\).) C'est la première indication que nous avons affaire à des dérivées partielles. Ensuite, nous avons maintenant deux dérivées différentes que nous pouvons prendre, puisqu'il existe deux variables indépendantes différentes. En fonction de la variable que nous choisissons, nous pouvons obtenir différentes dérivées partielles, et c'est souvent le cas.

Exemple\(\PageIndex{1}\): Calculating Partial Derivatives from the Definition

Utiliser la définition de la dérivée partielle comme limite pour calculer\(∂f/∂x\) et\(∂f/∂y\) pour la fonction

\[f(x,y)=x^2−3xy+2y^2−4x+5y−12. \nonumber \]

Solution

Commencez par calculer\(f(x+h,y).\)

\[\begin{align*} f(x+h,y) &=(x+h)^2−3(x+h)y+2y^2−4(x+h)+5y−12 \\ &=x^2+2xh+h^2−3xy−3hy+2y^2−4x−4h+5y−12. \end{align*} \nonumber \]

Ensuite, remplacez-le dans l'équation \ ref {pd1} et simplifiez :

\ [\ begin {align*} \ dfrac {δf} {δx} &= \ lim_ {h→0} \ dfrac {f (x+h, y) −f (x, y)} {h} \ \
&= \ lim_ {h→0} \ dfrac {(x^2+2xh+h^2−3xy−3hy+2y^2−4×2−4−4xh+h^2−3hy+2y^2−4x−4−4xh+2−3hy+2y^2−4−4−4xh−4h+5y−12) − (x^2−3xy+2y^2−4x+5y−12)} {h} \ \ &= \ lim_ {h→0} \ dfrac {x^2+2xh+h^2−3xy−3hy+2y^2−4x−4h+5y−12−x^2+3xy−2y−3y−3hy+2−4x−4h+5y−12−x^2+3xy−2y−3hy+2−4x−4h+5y−12−x^2−24x−5y+12} {h} \ \
&= \ lim_ {h→0} \ dfrac {2 xh+h^2−3hy−4h} {h} \ \ \
&= \ lim_ {h→0} \ dfrac {h (2x+h−3y−4)} {h} \ \
&= \ lim_ {h→0} (2x+h−3y−4) \ \ &=2x−3y−4) \ \
&=2x−3y−4. \ end {align*} \]

Pour calculer\(\dfrac{∂f}{∂y}\), commencez par calculer\(f(x,y+h):\)

\[\begin{align*} f(x+h,y) &=x^2−3x(y+h)+2(y+h)^2−4x+5(y+h)−12 \\ &=x^2−3xy−3xh+2y^2+4yh+2h^2−4x+5y+5h−12. \end{align*}\]

Ensuite, remplacez-le dans l'équation \ ref {pd2} et simplifiez :

\ [\ begin {align*} \ dfrac {δf} {y-y} &= \ lim_ {h→0} \ dfrac {f (x, y+h) −f (x, y)} {h} \ \
&= \ lim_ {h→0} \ dfrac {(x^2−3xy−3xy−3xh+2y^2+4yh+2h+2h^2+4yh+2h^0} \ dfrac {(x^2−3xy−3xh+2y^2+4yh+2h+2h^−4x+5an+5h−12) − (x^2−3xy+2y^2−4x+5y−12)} {h} \ \ &= \ lim_ {h→0} \ dfrac {x^2−3xy−3xh+2y^2+4yh+2h^2−4x+5y+5h−12−x^2+3xy2−2−2−4−4x+5y+5h−12−x^2+3xy2−2−2−2−4−4x+5y+5h−12−x^2−y^2+4x−5y+12} {h} \ \
&= \ lim_ {h→0} \ dfrac {−3xh+4yh+2h^2+5h} {h} \ \
&= \ lim_ {h→0} \ dfrac {h (−3x+4y+2h+5)} {h} \ \
&= \ lim_ {h→0} (−3x+4y+2h+5) \ \
&=−3x+4y+5 \ {fin aligner*} \]

Exercice\(\PageIndex{1}\)

Utiliser la définition de la dérivée partielle comme limite pour calculer\(∂f/∂x\) et\(∂f/∂y\) pour la fonction

\[f(x,y)=4x^2+2xy−y^2+3x−2y+5.\nonumber \]

Allusion

Utilisez les équations \ ref {pd1} et \ ref {pd2} issues de la définition des dérivées partielles.

Réponse

\(\dfrac{∂f}{∂x}=8x+2y+3\)

\(\dfrac{∂f}{∂y}=2x−2y−2\)

L'idée à garder à l'esprit lors du calcul des dérivées partielles est de traiter toutes les variables indépendantes, à l'exception de la variable par rapport à laquelle nous différencions, comme des constantes. Procédez ensuite à la différenciation comme avec une fonction d'une seule variable. Pour comprendre pourquoi cela est vrai, commencez par corriger\(y\) et définir\(g(x)=f(x,y)\) en fonction de\(x\). Alors

\[\begin{align*} g′(x) &=\lim_{h→0}\dfrac{g(x+h)−g(x)}{h} \\[6pt] &=\lim_{h→0}\dfrac{f(x+h,y)−f(x,y)}{h} \\[6pt] &=\dfrac{∂f}{∂x}. \end{align*}\]

Il en va de même pour le calcul de la dérivée partielle de\(f\) par rapport à\(y\). Cette fois, fixez\(x\) et\(h(y)=f(x,y)\) définissez en fonction de\(y\). Alors

\[\begin{align*} h′(x) &=\lim_{k→0}\dfrac{h(x+k)−h(x)}{k} \\[6pt] &=\lim_{k→0}\dfrac{f(x,y+k)−f(x,y)}{k} \\[6pt] &=\dfrac{∂f}{∂y}. \end{align*}\]

Toutes les règles de différenciation s'appliquent.

Exemple\(\PageIndex{2}\): Calculating Partial Derivatives

Calculez\(∂f/∂x\) et\(∂f/∂y\) pour les fonctions suivantes en maintenant constante la variable opposée puis en la différenciant :

1. \(f(x,y)=x^2−3xy+2y^2−4x+5y−12\)
2. \(g(x,y)=\sin(x^2y−2x+4)\)

Solution :

a. Pour calculer\(∂f/∂x\), traitez la variable\(y\) comme une constante. Faites ensuite la différence\(f(x,y)\) en\(x\) utilisant les règles de somme, de différence et de puissance :

\[\begin{align*}\dfrac{∂f}{∂x} &=\dfrac{∂}{∂x}\left[x^2−3xy+2y^2−4x+5y−12\right] \\[6pt] &=\dfrac{∂}{∂x}[x^2]−\dfrac{∂}{∂x}[3xy]+\dfrac{∂}{∂x}[2y^2]−\dfrac{∂}{∂x}[4x]+\dfrac{∂}{∂x}[5y]−\dfrac{∂}{∂x}[12] \\[6pt] &=2x−3y+0−4+0−0 \\ &=2x−3y−4. \end{align*}\]

Les dérivées des troisième, cinquième et sixième termes sont toutes nulles car elles ne contiennent pas la variable\(x\). Elles sont donc traitées comme des termes constants. La dérivée du second terme est égale au coefficient de\(x\), qui est\(−3y\). Calcul\(∂f/∂y\) :

\[\begin{align*} \dfrac{∂f}{∂y} &=\dfrac{∂}{∂y}\left[x^2−3xy+2y^2−4x+5y−12\right] \\[6pt] &=\dfrac{∂}{∂y}[x^2]−\dfrac{∂}{∂y}[3xy]+\dfrac{∂}{∂y}[2y^2]−\dfrac{∂}{∂y}[4x]+\dfrac{∂}{∂y}[5y]−\dfrac{∂}{∂y}[12] \\[6pt] &=−3x+4y−0+5−0 \\ &=−3x+4y+5. \end{align*} \nonumber \]

Ce sont les mêmes réponses obtenues dans l'exemple\(\PageIndex{1}\).

b. Pour calculer,\(∂g/∂x,\) traitez la variable y comme une constante. Faites ensuite la différence\(g(x,y)\) par rapport à\(x\) l'utilisation de la règle de chaîne et de la règle de puissance

\[\begin{align*}\dfrac{∂g}{∂x} &=\dfrac{∂}{∂x}\left[\sin(x^2y−2x+4)\right] \\[6pt] &=\cos(x^2y−2x+4)\dfrac{∂}{∂x}[x^2y−2x+4] \\[6pt] &=(2xy−2)\cos(x^2y−2x+4). \end{align*}\]

Pour calculer,\(∂g/∂y,\) traitez la variable\(x\) comme une constante. Faites ensuite la différence\(g(x,y)\) par rapport à\(y\) l'utilisation de la règle de chaîne et de la règle de puissance

\[ \begin{align*} \dfrac{∂g}{∂y} &=\dfrac{∂}{∂y}\left[\sin(x^2y−2x+4)\right] \\[6pt] &=\cos(x^2y−2x+4)\dfrac{∂}{∂y}[x^2y−2x+4] \\[6pt] &=x^2\cos(x^2y−2x+4). \end{align*} \nonumber \]

Exercice\(\PageIndex{2}\)

Calculer\(∂f/∂x\) et\(∂f/∂y\) pour la fonction

\[f(x,y)=\tan(x^3−3x^2y^2+2y^4) \nonumber \]

en maintenant la variable opposée constante, puis en la différenciant.

Allusion

Utilisez les équations \ ref {pd1} et \ ref {pd1} issues de la définition des dérivées partielles.

Réponse

\(\dfrac{∂f}{∂x}=(3x^2−6xy^2)\sec^2(x^3−3x^2y^2+2y^4)\)

\(\dfrac{∂f}{∂y}=(−6x^2y+8y^3)\sec^2(x^3−3x^2y^2+2y^4)\)

Comment interpréter ces dérivées partielles ? Rappelons que le graphe d'une fonction de deux variables est une surface dans\(R^3\). Si nous supprimons la limite de la définition de la dérivée partielle par rapport à\(x\), le quotient de différence demeure :

\[\dfrac{f(x+h,y)−f(x,y)}{h}. \nonumber \]

Cela ressemble au quotient de différence pour la dérivée d'une fonction d'une variable, à l'exception de la présence de la\(y\) variable. La figure\(\PageIndex{1}\) illustre une surface décrite par une fonction arbitraire\(z=f(x,y).\)

Figure\(\PageIndex{1}\) : Ligne de sécante passant par les points\((x,y,f(x,y))\) et\((x+h,y,f(x+h,y)).\)

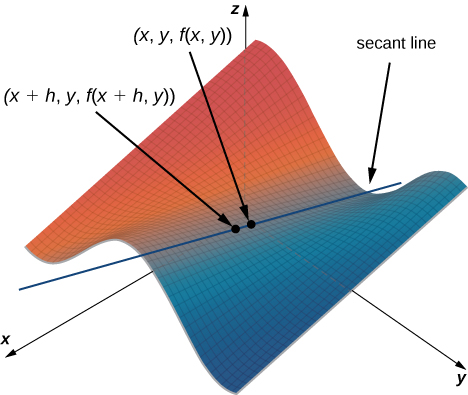
Dans la figure\(\PageIndex{1}\), la valeur de\(h\) est positive. Si nous graphions\(f(x,y)\) et\(f(x+h,y)\) pour un point arbitraire\((x,y),\), alors la pente de la droite sécante passant par ces deux points est donnée par

\[\dfrac{f(x+h,y)−f(x,y)}{h}. \nonumber \]

Cette ligne est parallèle à l'\(x\)axe. Par conséquent, la pente de la droite sécante représente le taux moyen de variation de la fonction lorsque\(f\) nous nous déplaçons parallèlement à l'\(x\)axe. Lorsque l'on\(h\) approche de zéro, la pente de la droite sécante se rapproche de la pente de la tangente.

Si nous choisissons de changer au\(y\) lieu\(x\) d'utiliser la même valeur incrémentielle\(h\), alors la droite sécante est parallèle à l'\(y\)axe -, de même que la droite tangente. \(∂f/∂x\)Représente donc la pente de la tangente passant par le point\((x,y,f(x,y))\) parallèle à l'\(x\)axe et\(∂f/∂y\) représente la pente de la tangente passant par le point\((x,y,f(x,y))\) parallèle à l'\(y\)axe. Si nous voulons trouver la pente d'une tangente passant par le même point dans une autre direction, nous avons besoin de ce que l'on appelle des dérivées directionnelles.

Nous revenons maintenant à l'idée des cartes de contour, que nous avons introduite dans Functions of Several Variables. Nous pouvons utiliser une carte de contour pour estimer les dérivées partielles d'une fonction\(g(x,y)\).

Exemple\(\PageIndex{3}\): Partial Derivatives from a Contour Map

Utiliser une carte de contour pour effectuer une estimation\(∂g/∂x\) au point\((\sqrt{5},0)\) de la fonction

\[g(x,y)=\sqrt{9−x^2−y^2}. \nonumber \]

Solution

La figure\(\PageIndex{2}\) représente une carte de contour pour la fonction\(g(x,y)\).

Figure\(\PageIndex{2}\) : Carte des contours de la fonction\(g(x,y)=\sqrt{9−x^2−y^2}\), utilisant\(c=0,1,2,\) et\(3 (c=3\) correspondant à l'origine).

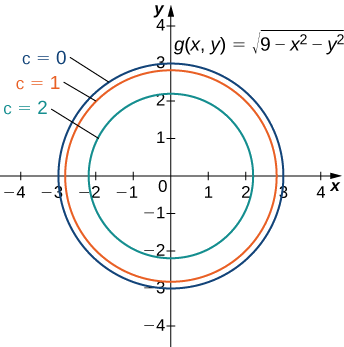
Le cercle intérieur sur la carte des contours correspond à\(c=2\) et le cercle suivant à la sortie correspond à\(c=1\). Le premier cercle est donné par l'équation\(2=\sqrt{9−x^2−y^2}\) ; le second cercle est donné par l'équation\(1=\sqrt{9−x^2−y^2}\). La première équation se simplifie à\(x^2+y^2=5\) et la seconde équation se\(x^2+y^2=8.\) simplifie en. L'\(x\)intersection du premier cercle est\((\sqrt{5},0)\) et l'\(x\)intersection du second cercle est\((2\sqrt{2},0)\). Nous pouvons estimer la valeur d'\(∂g/∂x\)évalué au point à l'\((\sqrt{5},0)\)aide de la formule de pente :

\[ \begin{align*} \left.\dfrac{∂g}{∂x}\right|_{(x,y) = (\sqrt{5},0)} &≈ \dfrac{g(\sqrt{5},0)−g(2\sqrt{2},0)}{\sqrt{5}−2\sqrt{2}} \\ &= \dfrac{2−1}{\sqrt{5}−2\sqrt{2}} \\ &=\dfrac{1}{\sqrt{5}−2\sqrt{2}} ≈−1.688. \end{align*}\]

Pour calculer la valeur exacte d'\(∂g/∂x\)évalué au point\((\sqrt{5},0)\), nous commençons par trouver à\(∂g/∂x\) l'aide de la règle de la chaîne. Tout d'abord, nous réécrivons la fonction comme

\[g(x,y)=\sqrt{9−x^2−y^2}=(9−x^2−y^2)^{1/2} \nonumber \]

puis différenciez par rapport à\(x\) tout en maintenant\(y\) constant :

\[ \begin{align*} \dfrac{∂g}{∂x} &=\dfrac{1}{2}(9−x^2−y^2)^{−1/2}(−2x) \\[4pt] &=−\dfrac{x}{\sqrt{9−x^2−y^2}}. \end{align*}\]

Ensuite, nous évaluons cette expression en utilisant\(x=\sqrt{5}\) et\(y=0\) :

\ [\ begin {align*} \ dfrac {δg} {δx} _ {(x, y) = (\ sqrt {5} ,0)} &=− \ dfrac {\ sqrt {5}} {\ sqrt {9− (\ sqrt {5}) ^2− (0) ^2}} \ \ [4 points] &=− \ sqrt {5})
^2− (0) ^2}} \ \ [4pt] &=− \ dfrac {\ sqrt {5}} {\ sqrt {4}} \ \ [4 points]
&=− \ dfrac {\ sqrt {5}} {2} ≈ −1,118. \ end {align*} \ nonumber \]

L'estimation de la dérivée partielle correspond à la pente de la droite sécante passant par les points\((\sqrt{5},0,g(\sqrt{5},0))\) et\((2\sqrt{2},0,g(2\sqrt{2},0))\). Elle représente une approximation de la pente de la tangente à la surface passant par\((\sqrt{5},0,g(\sqrt{5},0)),\) le point parallèle à l'\(x\)axe.

Exercice\(\PageIndex{3}\)

Utiliser une carte de contour pour estimer\(∂f/∂y\) le point\((0,\sqrt{2})\) de la fonction

\[ f(x,y)=x^2−y^2.\nonumber \]

Comparez cela avec la réponse exacte.

Allusion

Créez une carte de contours pour\(f\) utiliser des valeurs comprises\(c\) entre\(−3\) et\(3\). Laquelle de ces courbes passe par le point\((0,\sqrt{2})?\)

Réponse

En utilisant les courbes correspondantes à\(c=−2\) et\(c=−3,\) nous obtenons

\ [\ begin {align*} \ left. \ dfrac {δf} {δy} \ right|_ {(x, y) = (0, \ sqrt {2})} &≈ \ dfrac {f (0, \ sqrt {3}) −f (0, \ sqrt {2})} {\ sqrt {3} − \ sqrt {2}} \ \ [4 points] &= \ dfrac {−3} − \ sqrt {2}} \ \ [4 points]
&= \ dfrac {−3} − (−2)} {\ sqrt {3} − \ sqrt {2}} ⋅ \ dfrac {\ sqrt {3} + \ sqrt {2}} {\ sqrt {3} + \ sqrt {2}} \ \ [4 points]
&=− \ sqrt {3} − \ sqrt {2} ≈ −3,146. \ end {align*} \]

La réponse exacte est

\[ \left. \dfrac{∂f}{∂y} \right|_{(x,y)=(0,\sqrt{2})}=(−2y|_{(x,y)=(0,\sqrt{2})}=−2\sqrt{2}≈−2.828. \nonumber \]

Fonctions de plus de deux variables

Supposons que nous ayons une fonction de trois variables, telle que\(w=f(x,y,z).\) Nous pouvons calculer des dérivées partielles de\(w\) par rapport à n'importe laquelle des variables indépendantes, simplement en tant qu'extensions des définitions des dérivées partielles des fonctions de deux variables.

Définition : dérivées partielles

\(f(x,y,z)\)Soyons une fonction de trois variables. Ensuite, la dérivée partielle de\(f\) par rapport à\(x\), écrite comme\(∂f/∂x,\) ou\(f_x,\) est définie comme étant

\[\dfrac{∂f}{∂x}=f_x(x,y,z)=\lim_{h→0}\dfrac{f(x+h,y,z)−f(x,y,z)}{h}. \label{PD2a} \]

La dérivée partielle de\(f\) par rapport à\(y\), écrite comme\(∂f/∂y\), ou\(f_y\), est définie comme étant

\[\dfrac{∂f}{∂y}=f_y(x,y,z)=\lim_{k→0}\dfrac{f(x,y+k,z)−f(x,y,z)}{k.} \label{PD2b} \]

La dérivée partielle de\(f\) par rapport à\(z\), écrite comme\(∂f/∂z\), ou\(f_z\), est définie comme étant

\[\dfrac{∂f}{∂z}=f_z(x,y,z)=\lim_{m→0}\dfrac{f(x,y,z+m)−f(x,y,z)}{m}. \label{PD2c} \]

Nous pouvons calculer une dérivée partielle d'une fonction de trois variables en utilisant la même idée que celle que nous avons utilisée pour une fonction de deux variables. Par exemple, si nous avons une fonction\(f\) de et\(x,y\)\(z\), et que nous voulons calculer\(∂f/∂x\), nous traitons les deux autres variables indépendantes comme si elles étaient des constantes, puis nous les différencions par rapport à\(x\).

Exemple\(\PageIndex{4}\): Calculating Partial Derivatives for a Function of Three Variables

Utiliser la définition limite des dérivées partielles\(∂f/∂x\) pour calculer la fonction

\[ f(x,y,z)=x^2−3xy+2y^2−4xz+5yz^2−12x+4y−3z. \nonumber \]

Ensuite, trouvez\(∂f/∂y\) et\(∂f/∂z\) en définissant les deux autres variables constantes et en les différenciant en conséquence.

Solution :

Nous calculons d'abord\(∂f/∂x\) à l'aide de l'équation \ ref {PD2a}, puis nous calculons les deux autres dérivées partielles en maintenant constantes les variables restantes. Pour utiliser l'équation pour trouver\(∂f/∂x\), nous devons d'abord calculer\(f(x+h,y,z):\)

\ [\ begin {align*} f (x+h, y, z) &= (x+h) ^2−3 (x+h) y+2y^2−4 (x+h) z+5yz^2−12 (x+h) +4y−3z \ \ [4 points]
&=x^2+2xh+h^2−3xy−3xh+2y+2y+2y−3xy−3xh+2y+2y+3xy−3xh+2y+2y+3xy−3xh+2y+2y+^2−4xz−4hz+5yz^2−12x−12h+4y−3z \ end {align*} \ nonnumber \]

et rappelons que\(f(x,y,z)=x^2−3xy+2y^2−4zx+5yz^2−12x+4y−3z.\) Ensuite, nous substituons ces deux expressions dans l'équation :

\ [\ begin {align*} \ dfrac {δf} {δx} &= \ lim_ {h→0} \ left [\ dfrac {x^2+2xh+h^2−3xy−3hy+2y^2−4xz−4hz−4hz+5yz^2−12x−12h+4y−3zh−x^2−3xy+2y2^2−12h+4y−3zh−x^2−3xy+2y2^2^2−2^2^2−3zh−−4xz+5yz^2−12x+4y−3z} {h} \ droite] \ \ [4 points]
&= \ lim_ {h→0} \ left [\ dfrac {2xh+h^2−3hy−4hz−12h} {h} \ droite] \ \ [4 points]
&= \ lim_ {h→0} \ gauche [\ dfrac {h (2x+h−3y−4z−12) )} {h} \ droite] \ \ [4 points]
&= \ lim_ {h→0} (2x+h−3y−4z−12) \ \ [4 points]
&=2x−3y−4z−12. \ end {align*} \ nonumber \]

Ensuite, nous trouvons\(∂f/∂y\) en maintenant\(x\) et en\(z\) permanence. Par conséquent, tout terme qui n'inclut pas la variable\(y\) est constant et sa dérivée est nulle. Nous pouvons appliquer les règles de somme, de différence et de puissance aux fonctions d'une variable :

\ [\ begin {align*} & \ dfrac {,} {y-y} \ left [x^2−3xy+2y^2−4xz+5yz^2−12x+4y−3z \ right] \ \ [4 points]
&= \ dfrac {{{{et} {+ \ dfrac {} {asyy} [2y^2] − \ dfrac {{} {δy} [4xz] + \ dfrac {} {δy} [5yz^2] − \ dfrac {} {98-y} [12x] + \ dfrac {489} {z} [3z] \ \ [4 points]
&=0−3x+4y−0+5z^2−0+4−0 \ \ [4 points]
&=−3x+4 ans+5 z^2+4. \ end {align*} \]

Pour calculer,\(∂f/∂z,\) nous maintenons\(y\) une constante\(x\) et appliquons les règles de somme, de différence et de puissance pour les fonctions d'une variable :

\ [\ begin {align*} & \ dfrac {,} {δz} [x^2−3xy+2y^2−4xz+5yz^2−12x+4y−3z] \ \ [4pt]
&= \ dfrac {)} {⌘z} [x^2] − \ dfrac {ac {,} {δz} [2y^2] − \ dfrac {,} {δz} [4xz] + \ dfrac {,} {iqz} [5yz^2] − \ dfrac {} {iqz} [12x] + \ dfrac {} {lqz} [4y] − \ dfrac {z] \ \ [4 points]
&=0−0+0−4x+10 yz−0+0−3 \ \ [4 points]
&=−4x+10yz−3 \ end {align*} \]

Exercice\(\PageIndex{4}\)

Utiliser la définition limite des dérivées partielles\(∂f/∂x\) pour calculer la fonction

\[f(x,y,z)=2x^2−4x^2y+2y^2+5xz^2−6x+3z−8.\nonumber \]

Ensuite, trouvez\(∂f/∂y\) et\(∂f/∂z\) en définissant les deux autres variables constantes et en les différenciant en conséquence.

Allusion

Utilisez la stratégie de l'exemple précédent.

Réponse

\(\dfrac{∂f}{∂x}=4x−8xy+5z^2−6,\dfrac{∂f}{∂y}=−4x^2+4y,\dfrac{∂f}{∂z}=10xz+3\)

Exemple\(\PageIndex{5}\): Calculating Partial Derivatives for a Function of Three Variables

Calculez les trois dérivées partielles des fonctions suivantes.

1. \(f(x,y,z)=x^2y−4xz+y^2x−3yz\)
2. \(g(x,y,z)=\sin(x^2y−z)+\cos(x^2−yz)\)

Solution

Dans chaque cas, traitez toutes les variables comme des constantes, sauf celle dont vous calculez la dérivée partielle.

un.

\ [\ begin {align*} \ dfrac {δf} {δx} &= \ dfrac {,} {δx} \ left [\ dfrac {x^2y−4xz+y^2} {x−3yz} \ droite] \ \ [6pt]
&= \ dfrac {\ dfrac {+y^2) (x−3yz) − (x^2y−4xz+y^2) \ dfrac {} {δx} (x−3yz)} {(x−3yz) ^2} \ \ [6 points]
&= \ dfrac {(2xy−4z) (x−3yz) − (x−2y−4xz+yz) 2) (1)} {(x−3yz) ^2} \ \ [6 points]
&= \ dfrac {2x^2y−6xy^2z−4xz+12yz^2−x^2y+4xz−y^2} {(x−3yz) ^2} \ \ [6pt]
&= \ dfrac {x^2y−6xy^2z−4xz+12yz^2+4xz−y^2} {(x−3−yz) ^2} {(x−3−yz) yz) ^2} \ end {align*} \]

\ [\ begin {align*} \ dfrac {36.f} {y-y} &= \ dfrac {} {y-y} \ left [\ dfrac {x^2y−4xz+y^2} {x−3yz} \ droite] \ \ [6pt]
&= \ dfrac {\ dfrac {+y^2) (x−3yz) − (x^2y−4xz+y^2) \ dfrac {} {δy} (x−3yz)} {(x−3yz) ^2} \ \ [6 points]
&= \ dfrac {(x^2+2y) (x−3yz) − (x^2y−4xz+yz) ^2) (−3z)} {(x−3 yz) ^2} \ \ [6 points]
&= \ dfrac {x^3−3x^2yz+2xy−6y^2z+3x^2yz−12xz^2+3y^2z} {(x−3yz) ^2} \ \ [6 points]
&= \ dfrac {x^3+2xy−3y^2z−12xz^2} {(x−3y^2z−12xz^2} {(x−3y−z^2} z) ^2} \ end {align*} \]

\ [\ begin {align*} \ dfrac {δf} {bizz} &= \ dfrac {{363 z} \ left [\ dfrac {x^2y−4xz+y^2} {x−3yz} \ droite] \ \ [6pt]
&= \ dfrac {\ dfrac {+y^2) (x−3yz) − (x^2y−4xz+y^2) \ dfrac {} {δz} (x−3yz)} {(x−3yz) ^2} \ \ [6 points]
&= \ dfrac {(−4x) (x−3yz) − (x^2y−4xz+y^2) (−3 y)} {(x−3 yz) ^2} \ \ [6 points]
&= \ dfrac {−4x^2+12xyz+3x^2y^2−12xyz+3y^3} {(x−3yz) ^2} \ \ [6 points]
&= \ dfrac {−4x^2+3x^2y^2+3y^3} {(x−3yz) ^2} \ end {align*} \]

b.

\ [\ begin {align*} \ dfrac {36.f} {δx} &= \ dfrac {} {δx} \ left [\ sin (x^2y−z) + \ cos (x^2−yz) \ right] \ \ [6pt]
& =( \ cos (x^2y−z)) \ dfrac {} {⌘x} (x2^2y−z) y−z) − (\ sin (x^2−yz)) \ dfrac {} {δx} (x^2−yz) \ \ [6pt]
&=2xy \ cos (x^2y−z) −2x \ sin (x^2−yz) \ end {align*} \]

\ [\ begin {align*} \ dfrac {36.f} {y-y} &= \ dfrac {} {δy} [\ sin (x^2y−z) + \ cos (x^2−yz)] \ \ [6pt]
& =( \ cos (x^2y−z)) \ dfrac {− (\ sin (x^2−yz)) \ dfrac {} {δy} (x^2−yz) \ \ [6 points]
&=x^2 \ cos (x^2y−z) +z \ sin (x^2−yz) \ end {align*} \]

\ [\ begin {align*} \ dfrac {36.f} {δz} &= \ dfrac {,} {δz} [\ sin (x^2y−z) + \ cos (x^2−yz)] \ \ [6pt]
& =( \ cos (x^2y−z)) \ dfrac {− (\ sin (x^2−yz)) \ dfrac {} {δz} (x^2−yz) \ \ [6pt]
&=− \ cos (x^2y−z) +y \ sin (x^2−yz) \ end {align*} \ nonumber \]

Exercice\(\PageIndex{5}\)

Calculer\(∂f/∂x, ∂f/∂y,\) et\(∂f/∂z\) pour la fonction

\[f(x,y,z)=\sec(x^2y)−\tan(x^3yz^2). \nonumber \]

Allusion

Utilisez la stratégie de l'exemple précédent.

Réponse

\(\dfrac{∂f}{∂x}=2xy\sec(x^2y)\tan(x^2y)−3x^2yz^2\sec^2(x^3yz^2)\)

\(\dfrac{∂f}{∂y}=x^2\sec(x^2y)\tan(x^2y)−x^3z^2\sec^2(x^3yz^2)\)

\(\dfrac{∂f}{∂z}=−2x^3yz\sec^2(x^3yz^2)\)

Dérivées partielles d'

Considérez la fonction

\[f(x,y)=2x^3−4xy^2+5y^3−6xy+5x−4y+12. \nonumber \]

Ses dérivés partiels sont

\[\dfrac{∂f}{∂x}=6x^2−4y^2−6y+5 \nonumber \]

et

\[\dfrac{∂f}{∂y}=−8xy+15y^2−6x−4. \nonumber \]

Chacune de ces dérivées partielles est fonction de deux variables, nous pouvons donc calculer des dérivées partielles de ces fonctions. Tout comme pour les dérivées de fonctions à variable unique, nous pouvons les appeler dérivées du second ordre, des dérivées du troisième ordre, etc. En général, elles sont appelées dérivées partielles d'ordre supérieur. Il existe quatre dérivées partielles du second ordre pour chaque fonction (à condition qu'elles existent toutes) :

\ [\ begin {align*} \ dfrac {δ^2f} {tribunx^2} &= \ dfrac {,} {δx} \ left [\ dfrac {δf} {iqx} \ droite] \ \ [4pt]
 \ dfrac {⌘^2f} {ouffy⌘x} &= \ dfrac {} {situy} \ left [\ dfrac {} \ left [\ dfrac {frac {δf} {δx} \ droite]
 \ \ [4 points] \ dfrac {δ^2f} {δxδy} &= \ dfrac {} {δx} \ gauche [\ dfrac {⌘f} {298} \ droite] \ \ [4 points]
 \ dfrac {⌘^2f} {situy^2} &= \ dfrac {} {δy} \ left [\ dfrac {δf} {△ y} \ droite]. \ end {align*} \]

Une notation alternative pour chacun est\(f_{xx},f_{xy},f_{yx},\) et\(f_{yy}\), respectivement. Les dérivées partielles d'ordre supérieur calculées par rapport à différentes variables, telles que\(f_{xy}\) et\(f_{yx}\), sont communément appelées dérivées partielles mixtes.

Exemple\(\PageIndex{6}\): Calculating Second Partial Derivatives

Calculez les dérivées partielles des quatre secondes pour la fonction

\[f(x,y)=xe^{−3y}+\sin(2x−5y).\label{Ex6e1} \]

Solution :

Pour calculer\(\dfrac{∂^2f}{∂x^2}\) et\(\dfrac{∂^2f}{∂y∂x}\), nous calculons d'abord\(∂f/∂x\) :

\[\dfrac{∂f}{∂x}=e^{−3y}+2\cos(2x−5y). \label{Ex6e2} \]

Pour calculer\(\dfrac{∂^2f}{∂x^2}\), différenciez\(∂f/∂x\) (Équation \ ref {ex6E2}) par rapport à\(x\) :

\ [\ begin {align*} \ dfrac {département^2f} {δx^2} &= \ dfrac {} {δx} \ left [\ dfrac {δf} {iqf}} \ droite] \ \ [6 points]
&= \ dfrac {± 6 points] &= \ dfrac {± 4} {−3 y} +2 \ cos (2x−5 ans)] \ [6 points]
&=−4 \ sin (2x−5 ans). \ end {align*} \ nonumber \]

Pour calculer\(\dfrac{∂^2f}{∂y∂x}\), différenciez\(∂f/∂x\) (Équation \ ref {ex6E2}) par rapport à\(y\) :

\ [\ begin {align*} \ dfrac {δ^2f} {δy \, δx} &= \ dfrac {{¾} {δy} \ left [\ dfrac {astf} {ultrum} \ droite] \ \ [6 points]
&= \ dfrac {} {66.y} [e^ {−3y} +2 \ cos (2x−5 ans)] \ \ [6 points]
&=−3e^ {−3 ans} +10 \ sin (2x−5 ans). \ end {align*} \ nonumber \]

Pour calculer\(\dfrac{∂^2f}{∂x∂y}\) et\(\dfrac{∂^2f}{∂y^2}\), d'abord, calculer\(∂f/∂y\) :

\[\dfrac{∂f}{∂y}=−3xe^{−3y}−5\cos(2x−5y). \label{Ex6e5} \]

Pour calculer\(\dfrac{∂^2f}{∂x∂y}\), différenciez\(∂f/∂y\) (Équation \ ref {ex6E5}) par rapport à\(x\) :

\ [\ begin {align*} \ dfrac {δ^2f} {δxδy} &= \ dfrac {} {δx} \ left [\ dfrac {δf} {iqy} \ droite] \ \ [6 points] &= \ dfrac {± 6 points]
&= \ dfrac {} {⌘x} [−3xe^ {−3y} −5 \ cos (2x−5 ans)] \ \ [6 points]
&=−3e^ {−3 ans} +10 \ sin (2 x − 5 ans). \ end {align*} \ nonumber \]

Pour calculer\(\dfrac{∂^2f}{∂y^2}\), différenciez\(∂f/∂y\) (Équation \ ref {ex6E5}) par rapport à\(y\) :

\ [\ begin {align*} \ dfrac {δ^2f} {δy^2} &= \ dfrac {{{δy} \ left [\ dfrac {δf} {iqy} \ droite] \ \ [6pt]
&= \ dfrac {± 5} {hya} [−3xe^ {−3y} −5 \ cos (2x−5 ans)] \ \ [6 points]
&=9xe^ {−3 ans} −25 \ sin (2 x − 5 ans). \ end {align*} \ nonumber \]

Exercice\(\PageIndex{6}\)

Calculez les dérivées partielles des quatre secondes pour la fonction

\[f(x,y)=\sin(3x−2y)+\cos(x+4y).\nonumber \]

Allusion

Suivez les mêmes étapes que dans l'exemple précédent.

Réponse

\(\dfrac{∂^2f}{∂x^2}=−9\sin(3x−2y)−\cos(x+4y)\)

\(\dfrac{∂^2f}{∂y∂x}=6\sin(3x−2y)−4\cos(x+4y)\)

\(\dfrac{∂^2f}{∂x∂y}=6\sin(3x−2y)−4\cos(x+4y)\)

\(\dfrac{∂^2f}{∂y^2}=−4\sin(3x−2y)−16\cos(x+4y)\)

À ce stade, nous devons remarquer que, à la fois dans l'exemple\(\PageIndex{6}\) et dans le point de contrôle, c'était vrai\(\dfrac{∂^2f}{∂y∂x}=\dfrac{∂^2f}{∂x∂y}\). Dans certaines conditions, c'est toujours vrai. En fait, c'est une conséquence directe du théorème suivant.

Égalité des dérivées partielles mixtes (théorème de Clairaut)

Supposons que cela\(f(x,y)\) soit défini sur un disque ouvert\(D\) qui contient le point\((a,b)\). Si les fonctions\(f_{xy}\) et\(f_{yx}\) sont activées en continu\(D\), alors\(f_{xy}=f_{yx}\).

Le théorème de Clairaut garantit que tant que les dérivées mixtes du second ordre sont continues, l'ordre dans lequel nous choisissons de différencier les fonctions (c'est-à-dire quelle variable passe en premier, puis en second, etc.) n'a pas d'importance. Il peut également être étendu aux dérivés d'ordre supérieur. La preuve du théorème de Clairaut se trouve dans les livres de calcul les plus avancés.

Deux autres dérivées partielles du second ordre peuvent être calculées pour n'importe quelle fonction.\(f(x,y).\) La dérivée partielle\(f_{xx}\) est égale à la dérivée partielle de\(f_x\) par rapport à\(x\), et\(f_{yy}\) est égale à la dérivée partielle de\(f_y\) par rapport à\(y\).

Équations aux dériv

Auparavant, nous avons étudié des équations différentielles dans lesquelles la fonction inconnue avait une variable indépendante. Une équation aux dérivées partielles est une équation qui implique une fonction inconnue de plus d'une variable indépendante et d'une ou de plusieurs de ses dérivées partielles. Exemples d'équations aux dérivées partielles :

\[\underset{\text{heat equation in two dimensions}}{u_t=c^2(u_{xx}+u_{yy})} \nonumber \]

\[\underset{\text{wave equation in two dimensions}}{u_{tt}=c^2(u_{xx}+u_{yy})} \nonumber \]

\[\underset{\text{Laplace’s equation in two dimensions}} {u_{xx}+u_{yy}=0} \nonumber \]

Dans les équations de chaleur et de vagues, la fonction inconnue\(u\) comporte trois variables indépendantes :\(t\)\(x\),, et\(y\) avec\(c\) est une constante arbitraire. Les variables indépendantes\(x\) et\(y\) sont considérées comme des variables spatiales, et la variable\(t\) représente le temps. Dans l'équation de Laplace, la fonction inconnue\(u\) possède deux variables indépendantes\(x\) et\(y\).

Exemple\(\PageIndex{7}\): A Solution to the Wave Equation

Vérifiez que

\[u(x,y,t)=5\sin(3πx)\sin(4πy)\cos(10πt) \nonumber \]

est une solution à l'équation des vagues

\[u_{tt}=4(u_{xx}+u_{yy}). \label{Ex7Eq2} \]

Solution

Tout d'abord, nous calculons\(u_{tt},u_{xx},\) et\(u_{yy}:\)

\ [\ begin {align*} u_ {tt} (x, y, t) &= \ dfrac {} {δt} \ left [\ dfrac {36.u} {δt} \ droite] \ \ [6pt]
&= \ dfrac {✔} {sut} [5 \ sin (3πx) \ sin (4πy) (−10π \ sin (10πx) t)] \ \ [6 points]
&= \ dfrac {} {δt} \ gauche [−50π \ sin (3πx) \ sin (4πy) \ sin (10 πt) \ droite] \ \ [6 points]
&=−500π^2 \ sin (3πx) \ sin (4πy) \ cos (10πt) \ fin {align*} \]

\ [\ begin {align*} u_ {xx} (x, y, t) &= \ dfrac {,} {δx} \ left [\ dfrac {36.u} {δx} \ droite] \ \ [6pt]
&= \ dfrac {{✔} {⌘x} \ left [15π \ cos (3πx) \ sin (4πy) \ cos (10πt)) \ right] \ \ [6 points]
&=−45π^2 \ sin (3πx) \ sin (4πy) \ cos (10 πt) \ end {align*} \]

\ [\ begin {align*} u_ {yy} (x, y, t) &= \ dfrac {} {δy} \ left [\ dfrac {36.u} {y-y} \ droite] \ \ [6pt]
&= \ dfrac {} {10πt) \ droite] \ \ [6 points]
&= \ dfrac {} {δy} \ gauche [20π \ sin (3πx) \ cos (4πy) \ cos (10 πt) \ droite] \ \ [6 points]
&=−80π^2 \ sin (3πx) \ sin (4πy) \ cos ( 10 πt). \ end {align*} \ nonumber \]

Ensuite, nous les remplaçons dans la partie droite de l'équation \ ref {Ex7Eq2} et simplifions :

\ [\ begin {align*} 4 (u_ {xx} +u_ {yy}) &=4 (−45π^2 \ sin (3πx) \ sin (4πy) \ cos (10πt) +−80π^2 \ sin (3πx) \ sin (4πy) \ cos (10πt)) \ \ [6pt]
&=4 (−125π^2) \ sin (3πx) \ sin (4πy) \ cos (10 πt)) \ \ [6 points]
&=−500π^2 \ sin (3πx) \ sin (4πy) \ cos (10 πt) \ \ [6 points]
&=u_ {tt}. \ end {align*} \]

Cela permet de vérifier la solution.

Exercice\(\PageIndex{7}\): A Solution to the Heat Equation

Vérifiez que

\[u(x,y,t)=2\sin \left(\dfrac{x}{3} \right)\sin\left(\dfrac{y}{4} \right)e^{−25t/16} \nonumber \]

est une solution à l'équation thermique

\[u_t=9(u_{xx}+u_{yy}). \nonumber \]

Allusion

Calculez les dérivées partielles et remplacez-les dans la partie droite.

Réponse

TBA

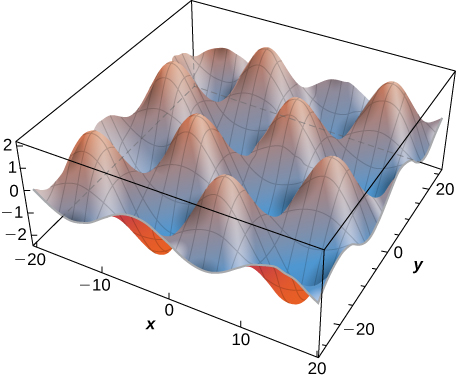
Comme la solution de l'équation thermique bidimensionnelle est fonction de trois variables, il n'est pas facile de créer une représentation visuelle de la solution. Nous pouvons représenter graphiquement la solution pour des valeurs fixes\(t,\), ce qui équivaut à des instantanés des distributions de chaleur à des moments fixes. Ces clichés montrent comment la chaleur est distribuée sur une surface bidimensionnelle au fil du temps. Le graphique de la solution précédente à l'époque\(t=0\) apparaît sur la figure\(\PageIndex{3}\). Au fil du temps, les extrêmes se stabilisent, s'approchant de zéro à mesure que l'infini se\(t\) rapproche.

Figurine\(\PageIndex{3}\)

Si nous considérons l'équation de la chaleur dans une dimension, il est alors possible de représenter graphiquement la solution au fil du temps. L'équation de la chaleur dans une dimension devient

\[u_t=c^2u_{xx}, \nonumber \]

où\(c^2\) représente la diffusivité thermique du matériau en question. Une solution de cette équation différentielle peut être écrite sous la forme

\[u_m(x,t)=e^{−π^2m^2c^2t}\sin(mπx) \nonumber \]

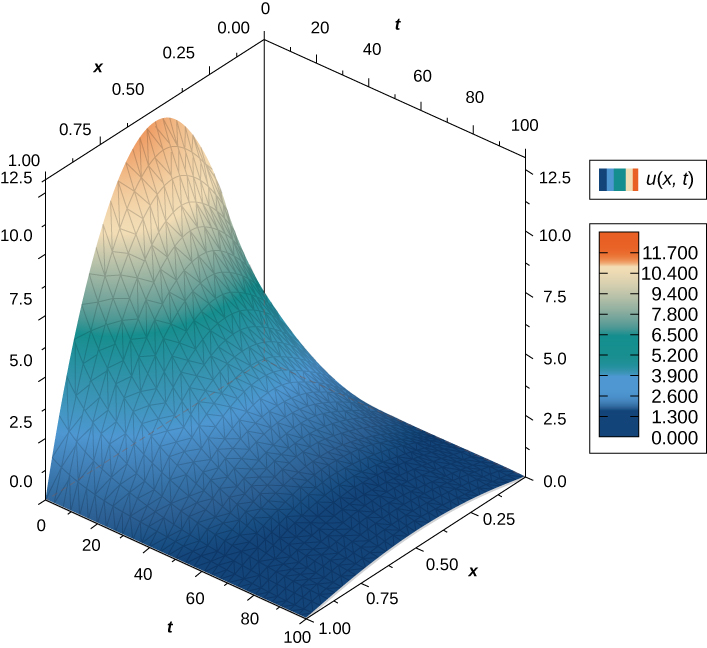
où\(m\) est un entier positif. Un graphique de cette utilisation de cette solution\(m=1\) apparaît sur la figure\(\PageIndex{4}\), où la distribution initiale de la température sur un fil de longueur\(1\) est donnée par\(u(x,0)=\sin πx.\) Notice qu'au fil du temps, le fil se refroidit. Cela est dû au fait que, de gauche à droite, la température la plus élevée (qui se produit au milieu du fil) diminue et change de couleur du rouge au bleu.

Figure\(\PageIndex{4}\) : Graphique d'une solution de l'équation de la chaleur dans une dimension au fil du temps.

Lord Kelvin et l'ère de la Terre

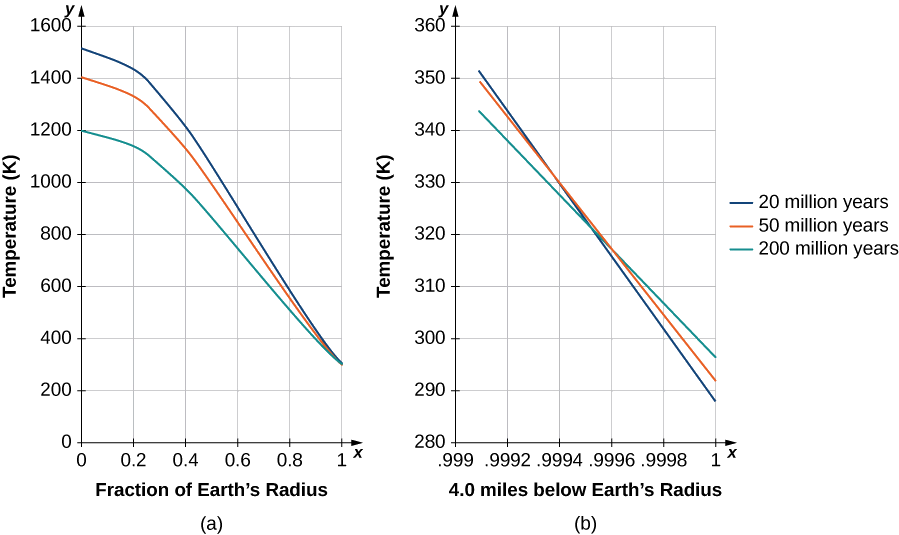
À la fin des années 1800, les scientifiques du nouveau domaine de la géologie arrivaient à la conclusion que la Terre devait avoir « des millions et des millions » d'années. À peu près à la même époque, Charles Darwin avait publié son traité sur l'évolution. Darwin était d'avis que l'évolution avait besoin de plusieurs millions d'années pour avoir lieu, et il a affirmé avec audace que les champs de craie de Weald, où d'importants fossiles ont été découverts, étaient le résultat de\(300\) millions d'années d'érosion.

Figure\(\PageIndex{5}\) : (a) William Thomson (Lord Kelvin), 1824-1907, était un physicien et ingénieur électricien britannique ; (b) Kelvin a utilisé l'équation de diffusion de la chaleur pour estimer l'âge de la Terre (crédit : modification des travaux de la NASA).

À cette époque, l'éminent physicien William Thomson (Lord Kelvin) a utilisé une importante équation aux dérivées partielles, connue sous le nom d'équation de diffusion de la chaleur, pour estimer l'âge de la Terre en déterminant le temps qu'il faudrait à la Terre pour se refroidir, passant de la roche en fusion à ce que nous avions à l'époque. Sa conclusion était une fourchette de 20 à 400 millions d'années, mais très probablement d'environ 50 millions d'années. Pendant de nombreuses décennies, les proclamations de cette icône incontestable de la science n'ont pas plu aux géologues ni à Darwin.

• Lisez l'article de Kelvin sur l'estimation de l'âge de la Terre.

Kelvin a fait des suppositions raisonnables en se basant sur ce que l'on savait à son époque, mais il a également fait plusieurs suppositions qui se sont révélées fausses. Une hypothèse erronée était que la Terre est solide et que le refroidissement s'est donc fait uniquement par conduction, ce qui justifie l'utilisation de l'équation de diffusion. Mais l'erreur la plus grave était une erreur pardonnable : l'omission du fait que la Terre contient des éléments radioactifs qui fournissent continuellement de la chaleur sous le manteau terrestre. La découverte de la radioactivité a eu lieu vers la fin de la vie de Kelvin et il a reconnu qu'il faudrait modifier ses calculs.

Kelvin a utilisé le modèle unidimensionnel simple appliqué uniquement à la couche extérieure de la Terre et a dérivé l'âge à partir de graphiques et du gradient de température à peu près connu près de la surface de la Terre. Examinons une version plus appropriée de l'équation de diffusion en coordonnées radiales, qui a la forme

\[\dfrac{∂T}{∂t}=K\left[\dfrac{∂^2T}{∂^2r}+\dfrac{2}{r}\dfrac{∂T}{∂r}\right] \label{kelvin1} \].

Ici, la température\(T(r,t)\) est fonction de\(r\) (mesurée à partir du centre de la Terre) et le temps\(t. K\) est la conductivité thermique, dans ce cas pour la roche en fusion. La méthode standard pour résoudre une telle équation aux dérivées partielles consiste à séparer les variables, où nous exprimons la solution comme le produit de fonctions contenant chaque variable séparément. Dans ce cas, on écrirait la température sous la forme

\[T(r,t)=R(r)f(t). \nonumber \]

1. Remplacez cette forme par l'équation \ ref {kelvin1} et, en notant qu'elle\(f(t)\) est constante par rapport à la distance\((r)\) et\(R(r)\) constante par rapport au temps\((t)\), montrez que\[\dfrac{1}{f}\dfrac{∂f}{∂t}=\dfrac{K}{R}\left[\dfrac{∂^2R}{∂r^2}+\dfrac{2}{r}\dfrac{∂R}{∂r}\right]. \nonumber \]
2. Cette équation représente la séparation des variables que nous voulons. Le côté gauche est uniquement fonction de\(t\) et le côté droit est uniquement fonction de\(r\), et ils doivent être égaux pour toutes les valeurs de\(r\) et\(t\). Par conséquent, elles doivent toutes deux être égales à une constante. Disons que c'est une constante\(−λ^2\). (La commodité de ce choix se voit lors de la substitution.) Donc, nous avons\[\dfrac{1}{f}\dfrac{∂f}{∂t}=−λ^2 \text{and} \dfrac{K}{R}\left[\dfrac{∂^2R}{∂r^2}+\dfrac{2}{r}\dfrac{∂R}{∂r}\right]=−λ^2. \nonumber \]
3. Nous pouvons maintenant vérifier, par substitution directe pour chaque équation\(R(r)=B\left(\dfrac{\sin αr}{r}\right)+C\left(\dfrac{\cos αr}{r}\right)\), que les solutions sont\(f(t)=Ae^{−λ^2t}\) et où\(α=λ/\sqrt{K}\). Notez que\(f(t)=Ae^{+λn^2t}\) c'est également une solution valable, nous aurions donc pu choisir\(+λ^2\) pour notre constante. Pouvez-vous comprendre pourquoi cela ne serait pas valable dans ce cas à mesure que le temps passe ?
4. Appliquons maintenant les conditions limites.
   1. La température doit être limitée au centre de la Terre,\(r=0\). Laquelle des deux constantes,\(B\) ou\(C\), doit donc être nulle pour maintenir la valeur\(R\) finie à zéro\(r=0\) ? (Rappelez-vous qu'il se comporte de\(\sin(αr)/r→α=\) manière très différente\(r→0\), mais qu'il\(\cos(αr)/r\) se comporte très différemment.
   2. Kelvin a soutenu que lorsque le magma atteint la surface de la Terre, il se refroidit très rapidement. Une personne peut souvent toucher la surface quelques semaines après l'écoulement. La surface a donc atteint une température modérée très tôt et est restée presque constante à température de surface\(T_s\). Par souci de simplicité,\(T=0\) fixons\(r=R_E\) et trouvons α de telle sorte que cette température soit là pour toujours\(t\). (Kelvin a pris la valeur\(300K≈80°F\). Nous pouvons ajouter cette\(300K\) constante à notre solution ultérieurement.) Pour que cela soit vrai, l'argument sinus doit être égal à zéro à\(r=R_E\). Notez que α possède une série infinie de valeurs qui satisfont à cette condition. Chaque valeur de\(α\) représente une solution valide (chacune avec sa propre valeur pour\(A\)). La solution totale ou générale est la somme de toutes ces solutions.
   3. \(t=0,\)Nous supposons que toute la Terre était à une température initiale chaude\(T_0\) (Kelvin a supposé que c'était environ\(7000K\).) L'application de cette condition limite implique l'application plus avancée des coefficients de Fourier. Comme indiqué dans la partie b., chaque valeur de\(α_n\) représente une solution valide, et la solution générale est la somme de toutes ces solutions. Il en résulte une solution en série :\[T(r,t)=\left(\dfrac{T_0R_E}{π}\right)\sum_n\dfrac{(−1)^{n−1}}{n}e^{−λn^2t}\dfrac{\sin(α_nr)}{r} \nonumber \] où\(\; α_n=nπ/R_E\).

Notez que les valeurs de\(α_n\) proviennent de la condition limite appliquée dans la partie b. Le terme\(\dfrac{−1^{n−1}}{n}\) est la constante\(A_n\) pour chaque terme de la série, déterminée en appliquant la méthode de Fourier. Examinons les premiers termes de cette solution présentée ici et remarquons comment,\(λ^2\) dans l'exponentielle, les termes supérieurs diminuent rapidement au fil du temps :\(β=\dfrac{π}{R_E}\)

\[T(r,t)=\dfrac{T_0R_E}{πr}\left(e^{−Kβ^2t}(\sinβr)−\dfrac{1}{2}e^{−4Kβ^2t}(\sin2βr)+\dfrac{1}{3}e^{−9Kβ^2t}(\sin3βr)−\dfrac{1}{4}e^{−16Kβ^2t}(\sin4βr)+\dfrac{1}{5}e^{−25Kβ^2t}(\sin5βr)...\right). \nonumber \]

Peu de temps\(t=0,\) après, de nombreux termes de la solution sont nécessaires pour des raisons de précision. En insérant des valeurs pour la conductivité\(K\) et\(β=π/R_E\) pour une durée approchant des milliers d'années, seuls les premiers termes apportent une contribution significative. Kelvin n'avait qu'à examiner la solution près de la surface de la Terre (Figure\(\PageIndex{6}\)) et, après un long moment, à déterminer quelle heure produisait le mieux le gradient de température estimé connu à son époque (\(1°F\)augmentation par\(50ft\)). Il a simplement choisi une plage de temps avec un gradient proche de cette valeur. Dans la figure\(\PageIndex{6}\), les solutions sont tracées et mises à l'échelle, en ajoutant la température de\(300−K\) surface. Notez que le centre de la Terre serait relativement frais. À l'époque, on pensait que la Terre devait être solide.

Figure\(\PageIndex{6}\) : Température par rapport à la distance radiale par rapport au centre de la Terre. (a) Les résultats de Kelvin, tracés à l'échelle. (b) Un gros plan des résultats à une profondeur de\(4.0\) miles sous la surface de la Terre.

Épilogue

Le 20 mai 1904, le physicien Ernest Rutherford a pris la parole à la Royal Institution pour annoncer un calcul révisé qui incluait la contribution de la radioactivité en tant que source de chaleur de la Terre. Pour reprendre les propres mots de Rutherford :

« Je suis entré dans la salle, qui faisait à moitié sombre, et j'ai vu Lord Kelvin dans l'assistance, et j'ai réalisé que j'avais des problèmes lors de la dernière partie de mon discours sur l'âge de la Terre, où mes points de vue étaient en conflit avec les siens. À mon grand soulagement, Kelvin s'est endormi profondément, mais alors que j'en suis arrivé au point important, j'ai vu le vieil oiseau s'asseoir, ouvrir un œil et me jeter un regard maléfique.

Puis une inspiration soudaine m'est venue, et j'ai dit que Lord Kelvin avait limité l'âge de la Terre, à condition qu'aucune nouvelle source [de chaleur] ne soit découverte. Cette déclaration prophétique faisait référence à ce que nous examinons maintenant ce soir, le radium ! Voici ! Le vieux garçon m'a rayonné dessus. »

Rutherford a calculé que l'âge de la Terre était d'environ 500 millions d'années. La valeur acceptée aujourd'hui de l'âge de la Terre est d'environ 4,6 milliards d'années.

Concepts clés

• Une dérivée partielle est une dérivée impliquant une fonction de plusieurs variables indépendantes.
• Pour calculer une dérivée partielle par rapport à une variable donnée, traitez toutes les autres variables comme des constantes et utilisez les règles de différenciation habituelles.
• Les dérivées partielles d'ordre supérieur peuvent être calculées de la même manière que les dérivées d'ordre supérieur.

Équations clés

Dérivée partielle\(f\) de par rapport à\(x\)\[\dfrac{∂f}{∂x}=\displaystyle{\lim_{h→0}\dfrac{f(x+h,y)−f(x,y)}{h}} \nonumber \]

Dérivée partielle\(f\) de par rapport à\(y\)\[\dfrac{∂f}{∂y}=\displaystyle{\lim_{k→0}\dfrac{f(x,y+k)−f(x,y)}{k}} \nonumber \]

Lexique

dérivées partielles d'ordre supérieur

dérivés partiels de second ordre ou supérieur, qu'il s'agisse de dérivés partiels mixtes

dérivés partiels mixtes

dérivées partielles de second ordre ou supérieur, dans lesquelles au moins deux des différenciations concernent des variables différentes

dérivée partielle

une dérivée d'une fonction de plus d'une variable indépendante dans laquelle toutes les variables sauf une sont maintenues constantes

équation différentielle partielle

une équation qui implique une fonction inconnue de plus d'une variable indépendante et d'une ou de plusieurs de ses dérivées partielles