14.2E : Exercices pour la section 14.2

Last updated
Save as PDF

Page ID: 197408

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

1) Utilisez les lois limites pour les fonctions de deux variables afin d'évaluer chaque limite inférieure, étant donné que$\displaystyle \lim_{(x,y)→(a,b)}f(x,y) = 5$ et$\displaystyle \lim_{(x,y)→(a,b)}g(x,y) = 2$.

$\displaystyle \lim_{(x,y)→(a,b)}\left[f(x,y) + g(x,y)\right]$
$\displaystyle \lim_{(x,y)→(a,b)}\left[f(x,y) g(x,y)\right]$
$\displaystyle \lim_{(x,y)→(a,b)}\left[ \dfrac{7f(x,y)}{g(x,y)}\right]$
$\displaystyle \lim_{(x,y)→(a,b)}\left[\dfrac{2f(x,y) - 4g(x,y)}{f(x,y) - g(x,y)}\right]$

Réponse

$\displaystyle \lim_{(x,y)→(a,b)}\left[f(x,y) + g(x,y)\right] = \displaystyle \lim_{(x,y)→(a,b)}f(x,y) + \displaystyle \lim_{(x,y)→(a,b)}g(x,y)= 5 + 2 = 7$
$\displaystyle \lim_{(x,y)→(a,b)}\left[f(x,y) g(x,y)\right] =\left(\displaystyle \lim_{(x,y)→(a,b)}f(x,y)\right) \left(\displaystyle \lim_{(x,y)→(a,b)}g(x,y)\right) = 5(2) = 10$
$\displaystyle \lim_{(x,y)→(a,b)}\left[ \dfrac{7f(x,y)}{g(x,y)}\right] = \frac{7\left(\displaystyle \lim_{(x,y)→(a,b)}f(x,y)\right)}{\displaystyle \lim_{(x,y)→(a,b)}g(x,y)}=\frac{7(5)}{2} = 17.5$
$\displaystyle \lim_{(x,y)→(a,b)}\left[\dfrac{2f(x,y) - 4g(x,y)}{f(x,y) - g(x,y)}\right] = \frac{2\left(\displaystyle \lim_{(x,y)→(a,b)}f(x,y)\right) - 4 \left(\displaystyle \lim_{(x,y)→(a,b)}g(x,y)\right)}{\displaystyle \lim_{(x,y)→(a,b)}f(x,y) - \displaystyle \lim_{(x,y)→(a,b)}g(x,y)}= \frac{2(5) - 4(2)}{5 - 2} = \frac{2}{3}$

Dans les exercices 2 à 4, trouvez la limite de la fonction.

2)$\displaystyle \lim_{(x,y)→(1,2)}x$

3)$\displaystyle \lim_{(x,y)→(1,2)}\frac{5x^2y}{x^2+y^2}$

Réponse: $\displaystyle \lim_{(x,y)→(1,2)}\frac{5x^2y}{x^2+y^2} = 2$

4) Montrez que la limite$\displaystyle \lim_{(x,y)→(0,0)}\frac{5x^2y}{x^2+y^2}$ existe et est la même le long des trajectoires :$y$ -axe et$x$ -axe, et le long$ y=x$.

Dans les exercices 5 à 19, évaluez les limites aux valeurs indiquées de$x$ et$y$. Si la limite n'existe pas, indiquez-la et expliquez pourquoi elle n'existe pas.

5)$\displaystyle \lim_{(x,y)→(0,0)}\frac{4x^2+10y^2+4}{4x^2−10y^2+6}$

Réponse: $\displaystyle \lim_{(x,y)→(0,0)}\frac{4x^2+10y^2+4}{4x^2−10y^2+6} = \frac{2}{3} $

6)$\displaystyle \lim_{(x,y)→(11,13)}\sqrt{\frac{1}{xy}}$

7)$\displaystyle \lim_{(x,y)→(0,1)}\frac{y^2\sin x}{x}$

Réponse: $\displaystyle \lim_{(x,y)→(0,1)}\frac{y^2\sin x}{x} = 1$

8)$\displaystyle \lim_{(x,y)→(0,0)}\sin(\frac{x^8+y^7}{x−y+10})$

9)$\displaystyle \lim_{(x,y)→(π/4,1)}\frac{y\tan x}{y+1}$

Réponse: $\displaystyle \lim_{(x,y)→(π/4,1)}\frac{y\tan x}{y+1}=\frac{1}{2}$

10)$\displaystyle \lim_{(x,y)→(0,π/4)}\frac{\sec x+2}{3x−\tan y}$

11)$\displaystyle \lim_{(x,y)→(2,5)}(\frac{1}{x}−\frac{5}{y})$

Réponse: $\displaystyle \lim_{(x,y)→(2,5)}(\frac{1}{x}−\frac{5}{y}) = −\frac{1}{2}$

(12)$\displaystyle \lim_{(x,y)→(4,4)}x\ln y$

(13)$\displaystyle \lim_{(x,y)→(4,4)}e^{−x^2−y^2}$

Réponse: $\displaystyle \lim_{(x,y)→(4,4)}e^{−x^2−y^2} = e^{−32}$

(14)$\displaystyle \lim_{(x,y)→(0,0)}\sqrt{9−x^2−y^2}$

(15)$\displaystyle \lim_{(x,y)→(1,2)}(x^2y^3−x^3y^2+3x+2y)$

Réponse: $\displaystyle \lim_{(x,y)→(1,2)}(x^2y^3−x^3y^2+3x+2y) = 11$

16)$\displaystyle \lim_{(x,y)→(π,π)}x\sin(\frac{x+y}{4})$

17)$\displaystyle \lim_{(x,y)→(0,0)}\frac{xy+1}{x^2+y^2+1}$

Réponse: $\displaystyle \lim_{(x,y)→(0,0)}\frac{xy+1}{x^2+y^2+1} = 1$

18)$\displaystyle \lim_{(x,y)→(0,0)}\frac{x^2+y^2}{\sqrt{x^2+y^2+1}−1}$

19)$\displaystyle \lim_{(x,y)→(0,0)}\ln(x^2+y^2)$

Réponse: La limite n'existe pas car lorsque$x$ les$y$ deux s'approchent de zéro, la fonction s'approche$ \ln 0$, ce qui n'est pas défini (approche l'infini négatif).

Dans les exercices 20 à 21, complétez la déclaration.

20) Un point$ (x_0,y_0)$ dans une région plane$ R$ est un point intérieur de$R$ if _________________.

21) Un point$ (x_0,y_0)$ dans une région plane$R$ est appelé point limite de$R$ si ___________.

Réponse: Chaque disque ouvert centré sur$ (x_0,y_0)$ contient des points intérieurs$ R$ et extérieurs$ R$.

Dans les exercices 22 à 25, utilisez des techniques algébriques pour évaluer la limite.

(22)$\displaystyle \lim_{(x,y)→(2,1)}\frac{x−y−1}{\sqrt{x−y}−1}$

23)$\displaystyle \lim_{(x,y)→(0,0)}\frac{x^4−4y^4}{x^2+2y^2}$

Réponse: $\displaystyle \lim_{(x,y)→(0,0)}\frac{x^4−4y^4}{x^2+2y^2} = 0$

(24)$\displaystyle \lim_{(x,y)→(0,0)}\frac{x^3−y^3}{x−y}$

25)$\displaystyle \lim_{(x,y)→(0,0)}\frac{x^2−xy}{\sqrt{x}−\sqrt{y}}$

Réponse: $\displaystyle \lim_{(x,y)→(0,0)}\frac{x^2−xy}{\sqrt{x}−\sqrt{y}} = 0$

Dans les exercices 26 à 27, évaluez les limites des fonctions de trois variables.

(26)$\displaystyle \lim_{(x,y,z)→(1,2,3)}\frac{xz^2−y^2z}{xyz−1}$

(27)$\displaystyle \lim_{(x,y,z)→(0,0,0)}\frac{x^2−y^2−z^2}{x^2+y^2−z^2}$

Réponse: La limite n'existe pas.

Dans les exercices 28 à 31, évaluez la limite de la fonction en déterminant la valeur à laquelle la fonction s'approche le long des chemins indiqués. Si la limite n'existe pas, expliquez pourquoi.

(28)$\displaystyle \lim_{(x,y)→(0,0)}\frac{xy+y^3}{x^2+y^2}$

a. Le long de l'$x$axe -$ (y=0)$

b. Le long de l'$y$axe Y$ (x=0)$

c. Le long du chemin$y=2x$

29) Évaluez$\displaystyle \lim_{(x,y)→(0,0)}\frac{xy+y^3}{x^2+y^2}$ en utilisant les résultats du problème précédent.

Réponse: La limite n'existe pas. La fonction aborde deux valeurs différentes selon des chemins différents.

(30)$\displaystyle \lim_{(x,y)→(0,0)}\frac{x^2y}{x^4+y^2}$

a. Le long de l'$x$axe -$ (y=0)$

b. Le long de l'$y$axe Y$ (x=0)$

c. Le long du chemin$y=x^2$

31) Évaluez$\displaystyle \lim_{(x,y)→(0,0)}\frac{x^2y}{x^4+y^2}$ en utilisant les résultats du problème précédent.

Réponse: La limite n'existe pas car la fonction s'approche de deux valeurs différentes le long des chemins.

Dans les exercices 32 à 35, discutez de la continuité de chaque fonction. Détermine la plus grande région du$xy$ plan -dans laquelle chaque fonction est continue.

32)$ f(x,y)=\sin(xy)$

33)$ f(x,y)=\ln(x+y)$

Réponse: La fonction$ f$ est continue dans la région$ y>−x.$

34)$ f(x,y)=e^{3xy}$

35)$ f(x,y)=\dfrac{1}{xy}$

Réponse: La fonction$f$ est continue à tous les points du$xy$ plan, à l'exception des points situés sur les$y$ axes$x$ - et.

Dans les exercices 36 à 38, déterminez la région dans laquelle la fonction est continue. Expliquez votre réponse.

36)$ f(x,y)=\dfrac{x^2y}{x^2+y^2}$

(37)$ f(x,y)=$$ \begin{cases}\dfrac{x^2y}{x^2+y^2} & if(x,y)≠(0,0)\\0 & if(x,y)=(0,0)\end{cases}$

Astuce :: Montrez que la fonction aborde différentes valeurs le long de deux chemins différents.

Réponse: La fonction est continue à$ (0,0)$ puisque la limite de la fonction at$ (0,0)$ est$ 0$ la même valeur de$ f(0,0).$

38)$ f(x,y)=\dfrac{\sin(x^2+y^2)}{x^2+y^2}$

39) Déterminez s'il$ g(x,y)=\dfrac{x^2−y^2}{x^2+y^2}$ est continu à$ (0,0)$.

Réponse: La fonction est discontinue à$ (0,0).$ La limite n'existe$ (0,0)$ pas et$ g(0,0)$ n'existe pas.

40) Créez un graphique à l'aide d'un logiciel graphique pour déterminer où la limite n'existe pas. Déterminez la région du plan de coordonnées dans laquelle$ f(x,y)=\dfrac{1}{x^2−y}$ est continu.

41) Déterminez la région du$xy$ plan -dans laquelle la fonction composite$ g(x,y)=\arctan(\frac{xy^2}{x+y})$ est continue. Utilisez la technologie pour étayer votre conclusion.

Réponse: Puisque la fonction$ \arctan x$ est continue, elle$ (−∞,∞), g(x,y)=\arctan(\frac{xy^2}{x+y})$ est continue là où$ z=\dfrac{xy^2}{x+y}$ est continue. La fonction interne$ z$ est continue sur tous les points du$xy$ plan, sauf là où,$ y=−x.$ ainsi,$ g(x,y)=\arctan(\frac{xy^2}{x+y})$ est continue sur tous les points du plan de coordonnées, sauf aux points où$ y=−x.$

42) Déterminez la région du$xy$ plan dans laquelle$ f(x,y)=\ln(x^2+y^2−1)$ est continu. Utilisez la technologie pour étayer votre conclusion. (Conseil : choisissez la plage de valeurs$ y$ avec soin !)$ x$

43) À quels points de l'espace est$ g(x,y,z)=x^2+y^2−2z^2$ continu ?

Réponse: Tous les points$ P(x,y,z)$ de l'espace

44) À quels points de l'espace est$ g(x,y,z)=\dfrac{1}{x^2+z^2−1}$ continu ?

45) Montrez ce qui$\displaystyle \lim_{(x,y)→(0,0)}\frac{1}{x^2+y^2}$ n'existe pas à$ (0,0)$ en traçant le graphe de la fonction.

Réponse

Le graphique augmente sans limite à mesure que$ x$ les$ y$ deux s'approchent de zéro.

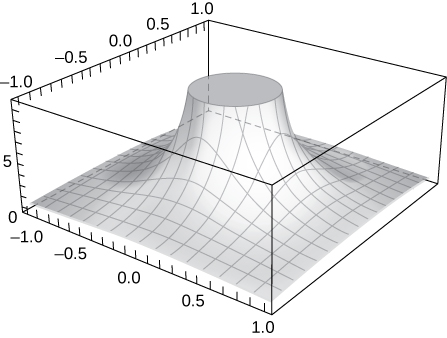
$Le graphique d'une surface où la coordonnée z augmente sans limite lorsque le point en entrée (x, y) s'approche de l'origine.$

46) [T] Évaluez$\displaystyle \lim_{(x,y)→(0,0)}\frac{−xy^2}{x^2+y^4}$ en traçant la fonction à l'aide d'un CAS. Déterminez analytiquement la limite le long du trajet$ x=y^2.$

47) [T]

a. Utilisez un CAS pour dessiner une carte de contour de$ z=\sqrt{9−x^2−y^2}$.

b. Quel est le nom de la forme géométrique des courbes de niveau ?

c. Donnez l'équation générale des courbes de niveau.

d. Quelle est la valeur maximale de$ z$ ?

e. Quel est le domaine de la fonction ?

f. Quelle est la portée de la fonction ?

Réponse

un.

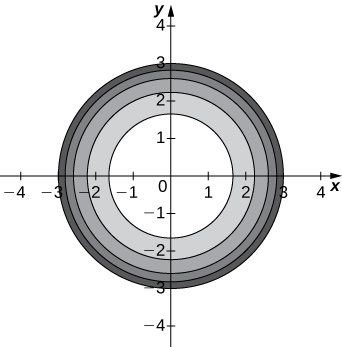
$Carte des contours de la fonction z=sqrt {9−x^2−y^2}$

b. Les courbes de niveau sont des cercles dont le centre est$ (0,0)$ un rayon$ 9−c$.
c.$ x^2+y^2=9−c$
d.$ z=3$
e.$ \{(x,y)∈R^2∣x^2+y^2≤9\}$
f.$ \{z|0≤z≤3\}$

48) Vrai ou faux : Si nous évaluons$\displaystyle \lim_{(x,y)→(0,0)}f(x)$ selon plusieurs voies et que chaque fois que la limite est atteinte$ 1$, nous pouvons en conclure que$\displaystyle \lim_{(x,y)→(0,0)}f(x)=1.$

49) Utilisez les coordonnées polaires pour trouver$\displaystyle \lim_{(x,y)→(0,0)}\frac{\sin\sqrt{x^2+y^2}}{\sqrt{x^2+y^2}}.$ Vous pouvez également trouver la limite en utilisant la règle de L'Hôpital.

Réponse: $\displaystyle \lim_{(x,y)→(0,0)}\frac{\sin\sqrt{x^2+y^2}}{\sqrt{x^2+y^2}} = 1$

50) Utilisez les coordonnées polaires pour trouver$\displaystyle \lim_{(x,y)→(0,0)}\cos(x^2+y^2).$

51) Discutez de la continuité$ f(g(x,y))$ entre où$ f(t)=1/t$ et$ g(x,y)=2x−5y.$

Réponse: $ f(g(x,y))$est continu à tous les points$ (x,y)$ qui ne se trouvent pas sur la ligne$ 2x−5y=0.$

52)$ f(x,y)=x^2−4y,$ Trouvaille donnée$\displaystyle \lim_{h→0}\frac{f(x+h,y)−f(x,y)}{h}.$

53)$ f(x,y)=x^2−4y,$ Trouvaille donnée$\displaystyle \lim_{h→0}\frac{f(1+h,y)−f(1,y)}{h}$.

Réponse: $ \displaystyle \lim_{h→0}\frac{f(1+h,y)−f(1,y)}{h} = 2$

Contributeurs

Template:ContribOpenStaxCalc
Paul Seeburger (Monroe Community College) created problem 1.