14.2 : Limites et continuité
- Page ID
- 197397
- Calculez la limite d'une fonction de deux variables.
- Découvrez comment une fonction composée de deux variables peut approcher différentes valeurs à un point limite, en fonction de la trajectoire d'approche.
- Indiquez les conditions de continuité d'une fonction à deux variables.
- Vérifiez la continuité d'une fonction de deux variables en un point.
- Calculez la limite d'une fonction de trois variables ou plus et vérifiez la continuité de la fonction en un point.
Nous avons maintenant examiné les fonctions de plusieurs variables et vu comment les représenter graphiquement. Dans cette section, nous verrons comment prendre la limite d'une fonction de plusieurs variables et ce que cela signifie pour une fonction de plusieurs variables d'être continue à un point de son domaine. Il s'avère que ces concepts présentent des aspects qui ne se produisent tout simplement pas avec les fonctions d'une variable.
Limite d'une fonction à deux variables
Rappelons dans la section 2.5 que la définition de la limite d'une fonction d'une variable :
\(f(x)\)Soit défini pour tous\(x≠a\) dans un intervalle ouvert contenant\(a\). \(L\)Soyons un vrai chiffre. Alors
\[\lim_{x→a}f(x)=L \nonumber \]
si pour tous\(ε>0,\) il existe un\(δ>0\), de telle sorte que si\(0<|x−a|<δ\) pour tous\(x\) se trouve dans le domaine de\(f\), alors
\[|f(x)−L|<ε. \nonumber \]
Avant de pouvoir adapter cette définition pour définir la limite d'une fonction à deux variables, nous devons d'abord voir comment étendre l'idée d'un intervalle ouvert dans une variable à un intervalle ouvert dans deux variables.
Considérons un point\((a,b)∈\mathbb{R}^2.\) Un\(δ\) disque centré sur un point\((a,b)\) est défini comme étant un disque ouvert dont le rayon est\(δ\) centré sur un point,\((a,b)\) c'est-à-dire
\[\{(x,y)∈\mathbb{R}^2∣(x−a)^2+(y−b)^2<δ^2\} \nonumber \]
comme le montre la figure\(\PageIndex{1}\).
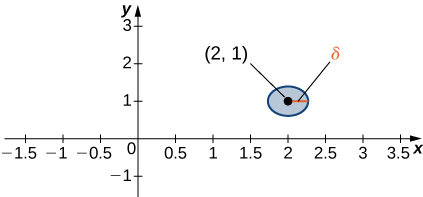
L'idée d'un\(δ\) disque apparaît dans la définition de la limite d'une fonction à deux variables. S'il\(δ\) est petit, tous\((x,y)\) les points du\(δ\) disque sont proches de\((a,b)\). Ceci est tout à fait analogue au fait que x est proche de a dans la définition de la limite d'une fonction d'une variable. Dans un sens, nous exprimons cette restriction comme
\[a−δ
Dans plus d'une dimension, nous utilisons un\(δ\) disque.
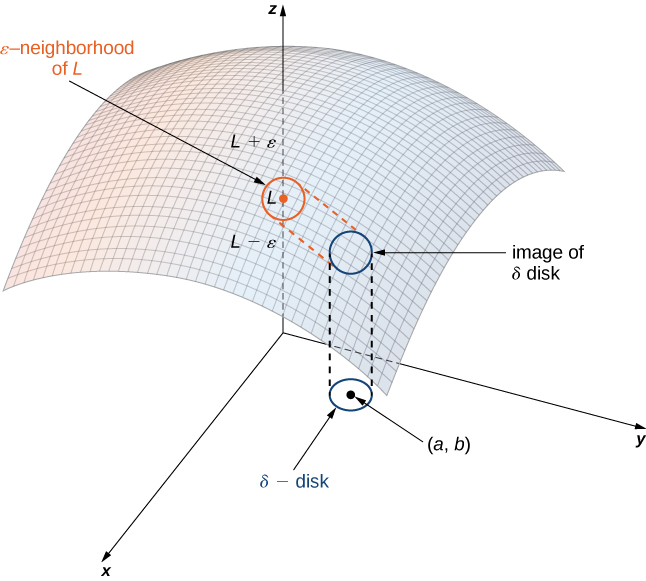
\(f\)Soyons une fonction de deux variables,\(x\) et\(y\). La limite de\(f(x,y)\) l'\((x,y)\)approche\((a,b)\) est\(L\), écrite
\[\lim_{(x,y)→(a,b)}f(x,y)=L \nonumber \]
s'\(ε>0\)il existe pour chacun une valeur suffisamment petite pour\(δ>0\) que, pour tous\((x,y)\) les points d'un\(δ\) disque environnant\((a,b)\), sauf éventuellement pour\((a,b)\) lui-même, la valeur de ne\(f(x,y)\) soit que\(ε\) éloignée de\(L\) (Figure\(\PageIndex{2}\)).
À l'aide de symboles, nous écrivons ce qui suit : Pour tout\(ε>0\), il existe un nombre\(δ>0\) tel que
\[|f(x,y)−L|<ε \nonumber \]
chaque fois que
\[0<\sqrt{(x−a)^2+(y−b)^2}<δ. \nonumber \]
Il peut être difficile de prouver l'existence d'une limite à l'aide de la définition de la limite d'une fonction à deux variables. Nous utilisons plutôt le théorème suivant, qui nous donne des raccourcis pour trouver des limites. Les formules de ce théorème sont une extension des formules du théorème des lois limites de The Limit Laws.
\(g(x,y)\)Soit\(f(x,y)\) défini pour tous les habitants d'un\((x,y)≠(a,b)\) quartier environnant\((a,b)\), et supposons que le quartier est entièrement contenu dans le domaine de\(f\). Supposons que\(L\) et que\(M\) les vrais nombres sont-ils tels que
\[\lim_{(x,y)→(a,b)}f(x,y)=L \nonumber \]
et
\[\lim_{(x,y)→(a,b)}g(x,y)=M, \nonumber \]
et\(c\) soyons une constante. Ensuite, chacune des affirmations suivantes est valable :
Loi constante :
\[\lim_{(x,y)→(a,b)}c=c \nonumber \]
Lois sur l'identité :
\[\lim_{(x,y)→(a,b)}x=a \nonumber \]
\[\lim_{(x,y)→(a,b)}y=b \nonumber \]
Loi sur la somme :
\[\lim_{(x,y)→(a,b)}(f(x,y)+g(x,y))=L+M \nonumber \]
Loi des différences :
\[\lim_{(x,y)→(a,b)}(f(x,y)−g(x,y))=L−M \nonumber \]
Loi multiple constante :
\[\lim_{(x,y)→(a,b)}(cf(x,y))=cL \nonumber \]
Loi sur les produits :
\[\lim_{(x,y)→(a,b)}(f(x,y)g(x,y))=LM \nonumber \]
Loi du quotient :
\[\lim_{(x,y)→(a,b)}\dfrac{f(x,y)}{g(x,y)}=\dfrac{L}{M} \text{ for } M≠0 \nonumber \]
Loi sur le pouvoir :
\[\lim_{(x,y)→(a,b)}(f(x,y))^n=L^n \nonumber \]
pour tout entier positif\(n\).
Loi fondamentale :
\[\lim_{(x,y)→(a,b)}\sqrt[n]{f(x,y)}=\sqrt[n]{L} \nonumber \]
pour tous\(L\) si\(n\) est impair et positif, et pour\(L≥0\) si n est pair et positif.
Les preuves de ces propriétés sont similaires à celles des limites des fonctions d'une variable. Nous pouvons appliquer ces lois pour déterminer les limites de diverses fonctions.
Déterminez chacune des limites suivantes :
- \(\displaystyle \lim_{(x,y)→(2,−1)}(x^2−2xy+3y^2−4x+3y−6)\)
- \(\displaystyle \lim_{(x,y)→(2,−1)}\dfrac{2x+3y}{4x−3y}\)
Solution
a. Utilisez d'abord les lois de somme et de différence pour séparer les termes :
\[\begin{align*} \lim_{(x,y)→(2,−1)}(x^2−2xy+3y^2−4x+3y−6)\\ = \left(\lim_{(x,y)→(2,−1)}x^2 \right)− \left(\lim_{(x,y)→(2,−1)}2xy \right)+ \left(\lim_{(x,y)→(2,−1)}3y^2 \right)−\left(\lim_{(x,y)→(2,−1)}4x\right) \\ + \left(\lim_{(x,y)→(2,−1)}3y \right)−\left(\lim_{(x,y)→(2,−1)}6\right). \end{align*}\]
Ensuite, utilisez la loi multiple constante sur les deuxième, troisième, quatrième et cinquième limites :
\[\begin{align*} =(\lim_{(x,y)→(2,−1)}x^2)−2(\lim_{(x,y)→(2,−1)}xy)+3(\lim_{(x,y)→(2,−1)}y^2)−4(\lim_{(x,y)→(2,−1)}x) \\[4pt] +3(\lim_{(x,y)→(2,−1)}y)−\lim_{(x,y)→(2,−1)}6.\end{align*}\]
Maintenant, utilisez la loi de puissance sur les première et troisième limites, et la loi du produit sur la deuxième limite :
\[\begin{align*} \left(\lim_{(x,y)→(2,−1)}x\right)^2−2\left(\lim_{(x,y)→(2,−1)}x\right) \left(\lim_{(x,y)→(2,−1)}y\right)+3\left(\lim_{(x,y)→(2,−1)}y\right)^2 \\ −4\left(\lim_{(x,y)→(2,−1)}x\right)+3\left(\lim_{(x,y)→(2,−1)}y\right)−\lim_{(x,y)→(2,−1)}6. \end{align*}\]
Enfin, utilisez les lois d'identité sur les six premières limites et la loi constante sur la dernière limite :
\[\begin{align*} \lim_{(x,y)→(2,−1)}(x^2−2xy+3y^2−4x+3y−6) = (2)^2−2(2)(−1)+3(−1)^2−4(2)+3(−1)−6 \\[4pt] =−6. \end{align*}\]
b. Avant d'appliquer la loi du quotient, nous devons vérifier que la limite du dénominateur n'est pas nulle. En utilisant la loi des différences, la loi multiple constante et la loi de l'identité,
\[\begin{align*} \lim_{(x,y)→(2,−1)}(4x−3y) =\lim_{(x,y)→(2,−1)}4x−\lim_{(x,y)→(2,−1)}3y \\[4pt] =4(\lim_{(x,y)→(2,−1)}x)−3(\lim_{(x,y)→(2,−1)}y) \\[4pt] =4(2)−3(−1)=11. \end{align*}\]
La limite du dénominateur étant différente de zéro, la loi du quotient s'applique. Nous calculons maintenant la limite du numérateur à l'aide de la loi des différences, de la loi multiple constante et de la loi de l'identité :
\[\begin{align*} \lim_{(x,y)→(2,−1)}(2x+3y) =\lim_{(x,y)→(2,−1)}2x+\lim_{(x,y)→(2,−1)}3y \\[4pt] =2(\lim_{(x,y)→(2,−1)}x)+3(\lim_{(x,y)→(2,−1)}y) \\[4pt] =2(2)+3(−1)=1. \end{align*}\]
Par conséquent, selon la loi du quotient, nous avons
\[\begin{align*} \lim_{(x,y)→(2,−1)}\dfrac{2x+3y}{4x−3y} =\dfrac{\displaystyle \lim_{(x,y)→(2,−1)}(2x+3y)}{\displaystyle \lim_{(x,y)→(2,−1)}(4x−3y)} \\[4pt] =\dfrac{1}{11}. \end{align*}\]
Évaluez la limite suivante :
\[\lim_{(x,y)→(5,−2)}\sqrt[3]{\dfrac{x^2−y}{y^2+x−1}}. \nonumber \]
- Allusion
-
Utilisez les lois limites.
- Réponse
-
\[\displaystyle \lim_{(x,y)→(5,−2)}\sqrt[3]{\dfrac{x^2−y}{y^2+x−1}}=\dfrac{3}{2} \nonumber \]
Puisque nous prenons la limite d'une fonction de deux variables, le point\((a,b)\) est\(\mathbb{R}^2\) dedans et il est possible de l'approcher depuis un nombre infini de directions. Parfois, lors du calcul d'une limite, la réponse varie en fonction du chemin emprunté\((a,b)\). Si tel est le cas, la limite n'existe pas. En d'autres termes, la limite doit être unique, quel que soit le chemin emprunté.
Montrez qu'aucune des limites suivantes n'existe :
- \(\displaystyle \lim_{(x,y)→(0,0)}\dfrac{2xy}{3x^2+y^2}\)
- \(\displaystyle \lim_{(x,y)→(0,0)}\dfrac{4xy^2}{x^2+3y^4}\)
Solution
a. Le domaine de la fonction\(f(x,y)=\dfrac{2xy}{3x^2+y^2}\) comprend tous les points du\(xy\) plan à l'exception du point\((0,0)\) (Figure\(\PageIndex{3}\)). Pour montrer que la limite n'existe pas à mesure que l'on\((x,y)\) approche\((0,0)\), on note qu'il est impossible de satisfaire à la définition d'une limite d'une fonction à deux variables du fait que la fonction prend des valeurs différentes le long de différentes lignes passant par le point\((0,0)\). Tout d'abord, considérez la ligne\(y=0\) dans le\(xy\) plan. La substitution\(y=0\) en\(f(x,y)\) donne
\[f(x,0)=\dfrac{2x(0)}{3x^2+0^2}=0 \nonumber \]
pour n'importe quelle valeur de\(x\). Par conséquent, la valeur de\(f\) reste constante pour n'importe quel point de l'\(x\)axe et, à mesure que l'on\(y\) approche de zéro, la fonction reste fixe à zéro.
Ensuite, considérez la ligne\(y=x\). La substitution\(y=x\) en\(f(x,y)\) donne
\[f(x,x)=\dfrac{2x(x)}{3x^2+x^2}=\dfrac{2x^2}{4x^2}=\tfrac{1}{2}. \nonumber \]
Cela est vrai pour n'importe quel point de la ligne\(y=x\). Si nous laissons l'\(x\)approche de zéro tout en restant sur cette ligne, la valeur de la fonction reste fixe\(\tfrac{1}{2}\), quelle que\(x\) soit sa taille.
Choisissez une valeur pour ε inférieure à\(1/2\) —say,\(1/4\). Ensuite, quelle que soit la taille\(δ\) du disque sur lequel nous dessinons\((0,0)\), les valeurs de\(f(x,y)\) quatre points à l'intérieur de ce\(δ\) disque incluront à la fois\(0\) et\(\tfrac{1}{2}\). Par conséquent, la définition de la limite à un moment donné n'est jamais satisfaite et la limite n'existe pas.
b. De la même manière que a., nous pouvons aborder l'origine le long de n'importe quelle ligne droite passant par l'origine. Si nous essayons l'\(x\)axe -( c'est-à-dire,\(y=0\)), la fonction reste fixée à zéro. Il en va de même pour l'\(y\)axe. Supposons que nous approchions de l'origine le long d'une ligne droite de pente\(k\). L'équation de cette droite est\(y=kx\). Ensuite, la limite devient
\[\begin{align*} \lim_{(x,y)→(0,0)}\dfrac{4xy^2}{x^2+3y^4} = \lim_{(x,y)→(0,0)}\dfrac{4x(kx)^2}{x^2+3(kx)^4} \\ = \lim_{(x,y)→(0,0)}\dfrac{4k^2x^3}{x^2+3k^4x^4} \\ =\lim_{(x,y)→(0,0)}\dfrac{4k^2x}{1+3k^4x^2} \\ = \dfrac{\displaystyle \lim_{(x,y)→(0,0)}(4k^2x)}{\displaystyle \lim_{(x,y)→(0,0)}(1+3k^4x^2)} \\ = 0. \end{align*}\]
quelle que soit la valeur de\(k\). Il semblerait que la limite soit égale à zéro. Et si nous choisissions plutôt une courbe passant par l'origine ? Par exemple, nous pouvons considérer la parabole donnée par l'équation\(x=y^2\). Substituer\(y^2\) à la place de\(x\) dans\(f(x,y)\) donne
\[\begin{align*}\lim_{(x,y)→(0,0)}\dfrac{4xy^2}{x^2+3y^4} = \lim_{(x,y)→(0,0)}\dfrac{4(y^2)y^2}{(y^2)^2+3y^4} \\ = \lim_{(x,y)→(0,0)}\dfrac{4y^4}{y^4+3y^4} \\ = \lim_{(x,y)→(0,0)}1 \\ = 1. \end{align*}\]
Selon la même logique, dans la partie a, il est impossible de trouver un disque δ autour de l'origine qui réponde à la définition de la limite pour toute valeur de\(ε<1.\) Par conséquent,
\[\displaystyle \lim_{(x,y)→(0,0)}\dfrac{4xy^2}{x^2+3y^4} \nonumber \]
n'existe pas.
Montrez que
\[\lim_{(x,y)→(2,1)}\dfrac{(x−2)(y−1)}{(x−2)^2+(y−1)^2} \nonumber \]
n'existe pas.
- Allusion
-
Choisissez une ligne dont la pente\(k\) passe par le point\((2,1).\)
- Réponse
-
Si\(y=k(x−2)+1,\) alors\(\lim_{(x,y)→(2,1)}\dfrac{(x−2)(y−1)}{(x−2)^2+(y−1)^2}=\dfrac{k}{1+k^2}\). Puisque la réponse dépend,\(k,\) la limite n'existe pas.
Points intérieurs et points limites
Pour étudier la continuité et la différentiabilité d'une fonction composée de deux variables ou plus, nous devons d'abord apprendre une nouvelle terminologie.
\(S\)Soyons un sous-ensemble de\(\mathbb{R}^2\) (Figure\(\PageIndex{4}\)).
- Un point\(P_0\) est appelé point intérieur\(S\) s'il y a un\(δ\) disque centré autour duquel il est complètement\(P_0\) contenu\(S\).
- Un point\(P_0\) est appelé point limite\(S\) si chaque\(δ\) disque centré\(P_0\) contient des points intérieurs et extérieurs\(S\).
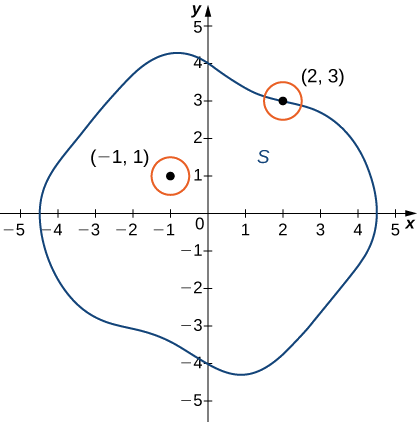
\(S\)Soyons un sous-ensemble de\(\mathbb{R}^2\) (Figure\(\PageIndex{4}\)).
- \(S\)est appelé ensemble ouvert si chaque point de\(S\) est un point intérieur.
- \(S\)est appelé ensemble fermé s'il contient tous ses points limites.
Un\(δ\) disque est un exemple d'ensemble ouvert. Si nous incluons la limite du disque, il devient un ensemble fermé. Un ensemble qui contient certains de ses points limites, mais pas tous, n'est ni ouvert ni fermé. Par exemple, si nous incluons la moitié de la limite d'un\(δ\) disque mais pas l'autre moitié, alors l'ensemble n'est ni ouvert ni fermé.
\(S\)Soyons un sous-ensemble de\(\mathbb{R}^2\) (Figure\(\PageIndex{4}\)).
- Un ensemble ouvert\(S\) est un ensemble connecté s'il ne peut pas être représenté comme l'union de deux ou plusieurs sous-ensembles ouverts non vides et disjoints.
- Un ensemble\(S\) est une région s'il est ouvert, connecté et non vide.
La définition d'une limite d'une fonction à deux variables nécessite que le\(δ\) disque soit contenu dans le domaine de la fonction. Toutefois, si nous voulons trouver la limite d'une fonction à un point limite du domaine, le\(δ\) disque n'est pas contenu à l'intérieur du domaine. Par définition, certains points du\(δ\) disque se trouvent à l'intérieur du domaine et d'autres à l'extérieur. Par conséquent, il suffit de prendre en compte les points situés à la fois dans le\(δ\) disque et dans le domaine de la fonction. Cela conduit à la définition de la limite d'une fonction à un point limite.
\(f\)Soyons une fonction de deux variables\(y\),\(x\) et supposons qu'\((a,b)\)il se trouve à la limite du domaine de\(f\). Ensuite, la limite\(f(x,y)\) de l'\((x,y)\)approche\((a,b)\) est\(L\) écrite
\[\lim_{(x,y)→(a,b)}f(x,y)=L, \nonumber \]
s'\(ε>0,\)il existe un nombre\(δ>0\) tel que pour tout point situé\((x,y)\) à l'intérieur du domaine\(f\) et à une distance suffisamment petite, le positif\(δ\) de\((a,b),\) la valeur de ne\(f(x,y)\) soit pas plus que\(ε\) éloigné\(L\) (Figure\(\PageIndex{2}\)). À l'aide de symboles, on peut écrire : Pour tous\(ε>0\), il existe un nombre\(δ>0\) tel que
\[|f(x,y)−L|<ε\, \text{whenever}\, 0<\sqrt{(x−a)^2+(y−b)^2}<δ. \nonumber \]
PROUVER
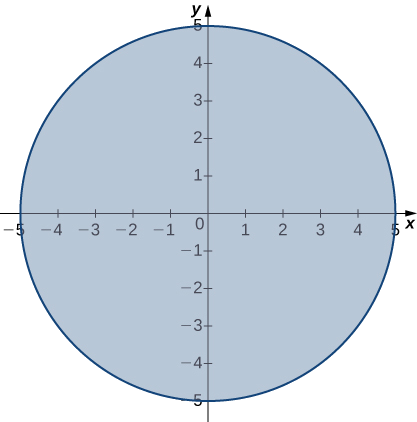
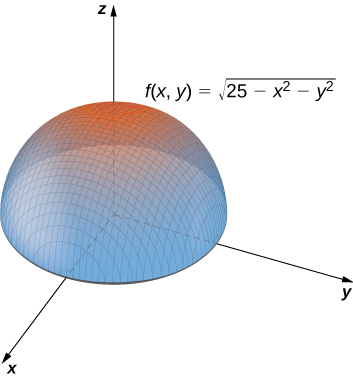
\[\lim_{(x,y)→(4,3)}\sqrt{25−x^2−y^2}=0. \nonumber \]
Solution
Le domaine de la fonction\(f(x,y)=\sqrt{25−x^2−y^2}\) est\(\big\{(x,y)∈\mathbb{R}^2∣x^2+y^2≤25\big\}\), qui est un cercle de rayon\(5\) centré à l'origine, ainsi que son intérieur, comme indiqué sur la figure\(\PageIndex{5}\).
Nous pouvons utiliser les lois limites, qui s'appliquent aux limites aux limites des domaines ainsi qu'aux points intérieurs :
\[\begin{align*} \lim_{(x,y)→(4,3)}\sqrt{25−x^2−y^2} =\sqrt{\lim_{(x,y)→(4,3)}(25−x^2−y^2)} \\ = \sqrt{\lim_{(x,y)→(4,3)}25−\lim_{(x,y)→(4,3)}x^2−\lim_{(x,y)→(4,3)}y^2} \\ =\sqrt{25−4^2−3^2} \\ = 0 \end{align*}\]
Reportez-vous au graphique suivant.
Évaluez la limite suivante :
\[\lim_{(x,y)→(5,−2)}\sqrt{29−x^2−y^2}. \nonumber \]
- Allusion
-
Déterminez le domaine de\(f(x,y)=\sqrt{29−x^2−y^2}\).
- Réponse
-
\[\lim_{(x,y)→(5,−2)}\sqrt{29−x^2−y^2} \nonumber \]
Continuité des fonctions de deux variables
Dans Continuité, nous avons défini la continuité d'une fonction d'une variable et avons vu comment elle reposait sur la limite d'une fonction d'une variable. En particulier, trois conditions sont nécessaires\(f(x)\) pour être continu au point\(x=a\)
- \(f(a)\)existe.
- \(\displaystyle \lim_{x→a}f(x)\)existe.
- \(\displaystyle \lim_{x→a}f(x)=f(a).\)
Ces trois conditions sont également nécessaires à la continuité d'une fonction de deux variables.
Une fonction\(f(x,y)\) est continue à un point\((a,b)\) de son domaine si les conditions suivantes sont remplies :
- \(f(a,b)\)existe.
- \(\displaystyle \lim_{(x,y)→(a,b)}f(x,y)\)existe.
- \(\displaystyle \lim_{(x,y)→(a,b)}f(x,y)=f(a,b).\)
Montrez que la fonction
\[f(x,y)=\dfrac{3x+2y}{x+y+1} \nonumber \]
est continu au point\((5,−3).\)
Solution
Trois conditions doivent être remplies, selon la définition de la continuité. Dans cet exemple,\(a=5\) et\(b=−3.\)
1. \(f(a,b)\)existe. Cela est vrai parce que le domaine de la fonction f est constitué des paires ordonnées pour lesquelles le dénominateur est différent de zéro (c'est-à-dire,\(x+y+1≠0\)). Le point\((5,−3)\) satisfait à cette condition. En outre,
\[f(a,b)=f(5,−3)=\dfrac{3(5)+2(−3)}{5+(−3)+1}=\dfrac{15−6}{2+1}=3. \nonumber \]
2. \(\displaystyle \lim_{(x,y)→(a,b)}f(x,y)\)existe. Cela est également vrai :
\[\begin{align*} \lim_{(x,y)→(a,b)}f(x,y) =\lim_{(x,y)→(5,−3)}\dfrac{3x+2y}{x+y+1} \\ =\dfrac{\displaystyle \lim_{(x,y)→(5,−3)}(3x+2y)}{\displaystyle \lim_{(x,y)→(5,−3)}(x+y+1)} \\ = \dfrac{15−6}{5−3+1} \\ = 3. \end{align*}\]
3. \(\displaystyle \lim_{(x,y)→(a,b)}f(x,y)=f(a,b).\)Cela est vrai parce que nous venons de montrer que les deux côtés de cette équation sont égaux à trois.
Montrez que la fonction
\[f(x,y)=\sqrt{26−2x^2−y^2}\nonumber \]
est continu au point\((2,−3)\).
- Allusion
-
Utilisez la définition en trois parties de la continuité.
- Réponse
-
- Le domaine de\(f\) contient la paire ordonnée\((2,−3)\) car\(f(a,b)=f(2,−3)=\sqrt{16−2(2)^2−(−3)^2}=3\)
- \(\displaystyle \lim_{(x,y)→(a,b)}f(x,y)=3\)
- \(\displaystyle \lim_{(x,y)→(a,b)}f(x,y)=f(a,b)=3\)
La continuité d'une fonction d'un nombre quelconque de variables peut également être définie en termes de delta et d'epsilon. Une fonction de deux variables est continue\((x_0,y_0)\) en un point de son domaine si, pour chacune, il en\(ε>0\) existe une\(δ>0\) telle que, chaque fois que\(\sqrt{(x−x_0)^2+(y−y_0)^2}<δ\) c'est vrai,\(|f(x,y)−f(a,b)|<ε.\) Cette définition peut être combinée avec la définition formelle (c'est-à-dire la définition epsilon—delta) de continuité d'une fonction d'une variable pour prouver les théorèmes suivants :
Si\(f(x,y)\) est continu à\((x_0,y_0)\), et\(g(x,y)\) est continu à\((x_0,y_0)\), alors\(f(x,y)+g(x,y)\) est continu à\((x_0,y_0)\).
Si\(g(x)\) est continu à\(x_0\) et\(h(y)\) est continu à\(y_0\), alors\(f(x,y)=g(x)h(y)\) est continu à\((x_0,y_0).\)
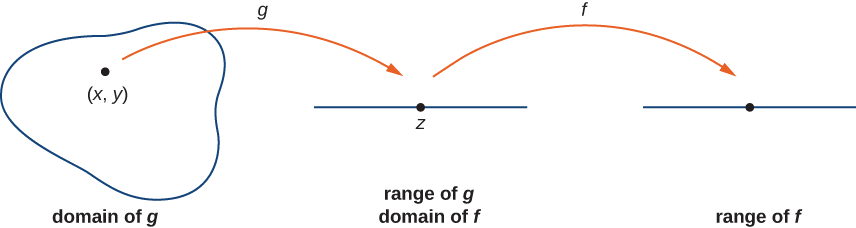
\(g\)Soyons une fonction de deux variables d'un domaine\(D⊆\mathbb{R}^2\) à une plage\(R⊆R.\) Supposons qu'elle\(g\) soit continue à un moment donné\((x_0,y_0)∈D\) et définissez-la\(z_0=g(x_0,y_0)\). Soit f une fonction qui correspond\(R\) à une fonction\(R\) qui\(z_0\) se trouve dans le domaine de\(f\). Enfin, supposons que\(f\) c'est continu à\(z_0\). Puis\(f∘g\) est continu\((x_0,y_0)\) comme indiqué sur la figure\(\PageIndex{7}\).
Utilisons maintenant les théorèmes précédents pour montrer la continuité des fonctions dans les exemples suivants.
Montrez que les fonctions\(f(x,y)=4x^3y^2\) et\(g(x,y)=\cos(4x^3y^2)\) sont continues partout.
Solution
Les polynômes\(g(x)=4x^3\) et\(h(y)=y^2\) sont continus à chaque nombre réel, et donc par le produit du théorème des fonctions continues,\(f(x,y)=4x^3y^2\) sont continus\((x,y)\) en tout point du\(xy\) plan. Comme elle\(f(x,y)=4x^3y^2\) est continue\((x,y)\) en tout point du\(xy\) plan et qu'elle\(g(x)=\cos x\) est continue à chaque nombre réel\(x\), la continuité de la composition des fonctions nous indique qu'elle\(g(x,y)=\cos(4x^3y^2)\) est continue\((x,y)\) en tout point du\(xy\) plan.
Montrez que les fonctions\(f(x,y)=2x^2y^3+3\) et\(g(x,y)=(2x^2y^3+3)^4\) sont continues partout.
- Allusion
-
Utilisez la continuité de la somme, du produit et de la composition de deux fonctions.
- Réponse
-
Les polynômes\(g(x)=2x^2\) et\(h(y)=y^3\) sont continus à chaque nombre réel ; par conséquent, par le produit du théorème des fonctions continues, ils\(f(x,y)=2x^2y^3\) sont continus\((x,y)\) en tout point du\(xy\) plan. De plus, toute fonction constante est continue partout, donc\(g(x,y)=3\) continue\((x,y)\) en tout point du\(xy\) plan. Par conséquent,\(f(x,y)=2x^2y^3+3\) est continu\((x,y)\) en tout point du\(xy\) plan. Enfin,\(h(x)=x^4\) est continu à chaque nombre réel\(x\), donc par la continuité des fonctions composites, le théorème\(g(x,y)=(2x^2y^3+3)^4\) est continu\((x,y)\) en tout point du\(xy\) plan.
Fonctions de trois variables ou plus
La limite d'une fonction de trois variables ou plus est facilement atteinte dans les applications. Supposons, par exemple, que nous ayons une fonction\(f(x,y,z)\) qui donne la température à un emplacement physique\((x,y,z)\) en trois dimensions. Ou peut-être qu'une fonction\(g(x,y,z,t)\) peut indiquer la pression de l'air à un endroit donné\((x,y,z)\) à la fois\(t\). Comment pouvons-nous fixer une limite à un moment donné\(\mathbb{R}^3\) ? Que signifie être continu en un point en quatre dimensions ?
Les réponses à ces questions reposent sur l'extension du concept de\(δ\) disque à plus de deux dimensions. Ensuite, les notions de limite d'une fonction de trois variables ou plus et de continuité d'une fonction de trois variables ou plus sont très similaires aux définitions données précédemment pour une fonction à deux variables.
\((x_0,y_0,z_0)\)Soyons un point\(\mathbb{R}^3\). Ensuite, une\(δ\) balle en trois dimensions est composée de tous les points\(\mathbb{R}^3\) situés à une\(δ\) distance inférieure à\((x_0,y_0,z_0)\)... c'est-à-dire
\[\big\{(x,y,z)∈\mathbb{R}^3∣\sqrt{(x−x_0)^2+(y−y_0)^2+(z−z_0)^2}<δ\big\}. \nonumber \]
Pour définir une\(δ\) balle dans des dimensions supérieures, ajoutez des termes supplémentaires sous le radical pour correspondre à chaque dimension supplémentaire. Par exemple, étant donné un point\(P=(w_0,x_0,y_0,z_0)\)\(\mathbb{R}^4\), une\(δ\) balle\(P\) peut être décrite par
\[\big\{(w,x,y,z)∈\mathbb{R}^4∣\sqrt{(w−w_0)^2+(x−x_0)^2+(y−y_0)^2+(z−z_0)^2}<δ\big\}. \nonumber \]
Pour montrer qu'une limite d'une fonction à trois variables existe en un point\((x_0,y_0,z_0)\), il suffit de montrer que pour tout point d'une\(δ\) boule centrée sur\((x_0,y_0,z_0)\), la valeur de la fonction en ce point est arbitrairement proche d'une valeur fixe (la valeur limite). Toutes les lois limites pour les fonctions de deux variables s'appliquent également aux fonctions de plus de deux variables.
Trouvez
\[\lim_{(x,y,z)→(4,1,−3)}\dfrac{x^2y−3z}{2x+5y−z}. \nonumber \]
Solution
Avant de pouvoir appliquer la loi du quotient, nous devons vérifier que la limite du dénominateur n'est pas nulle. En utilisant la loi de la différence, la loi de l'identité et la loi constante,
\[\begin{align*}\lim_{(x,y,z)→(4,1,−3)}(2x+5y−z) =2(\lim_{(x,y,z)→(4,1,−3)}x)+5(\lim_{(x,y,z)→(4,1,−3)}y)−(\lim_{(x,y,z)→(4,1,−3)}z) \\ = 2(4)+5(1)−(−3) \\ = 16. \end{align*}\]
Comme ce n'est pas zéro, on trouve ensuite la limite du numérateur. En utilisant la loi du produit, la loi du pouvoir, la loi des différences, la loi multiple constante et la loi de l'identité,
\[\begin{align*} \lim_{(x,y,z)→(4,1,−3)}(x^2y−3z) =(\lim_{(x,y,z)→(4,1,−3)}x)^2(\lim_{(x,y,z)→(4,1,−3)}y)−3\lim_{(x,y,z)→(4,1,−3)}z \\ =(4^2)(1)−3(−3) \\ = 16+9 \\ = 25 \end{align*}\]
Enfin, en appliquant la loi du quotient :
\[\lim_{(x,y,z)→(4,1,−3)}\dfrac{x^2y−3z}{2x+5y−z}=\dfrac{\displaystyle \lim_{(x,y,z)→(4,1,−3)}(x^2y−3z)}{\displaystyle \lim_{(x,y,z)→(4,1,−3)}(2x+5y−z)}=\dfrac{25}{16} \nonumber \]
Trouvez
\[\lim_{(x,y,z)→(4,−1,3)}\sqrt{13−x^2−2y^2+z^2} \nonumber \]
- Allusion
-
Utilisez les lois limites et la continuité de la composition des fonctions.
- Réponse
-
\[\lim_{(x,y,z)→(4,−1,3)}\sqrt{13−x^2−2y^2+z^2}=2 \nonumber \]
Concepts clés
- Pour étudier les limites et la continuité des fonctions de deux variables, nous utilisons un\(δ\) disque centré autour d'un point donné.
- Une fonction composée de plusieurs variables a une limite si, pour tout point d'une\(δ\) boule centré sur un point\(P\), la valeur de la fonction à ce point est arbitrairement proche d'une valeur fixe (la valeur limite).
- Les lois limites établies pour une fonction d'une variable s'étendent naturellement aux fonctions de plusieurs variables.
- Une fonction de deux variables est continue à un point si la limite existe à ce point, si la fonction existe à ce point et si la limite et la fonction sont égales à ce point.
Lexique
- point limite
- un point\(P_0\) de\(R\) est un point limite si chaque\(δ\) disque centré\(P_0\) contient des points intérieurs et extérieurs\(R\)
- set fermé
- un ensemble\(S\) contenant tous ses points limites
- ensemble connecté
- un ensemble ouvert\(S\) qui ne peut pas être représenté comme l'union de deux ou plusieurs sous-ensembles ouverts disjoints et non vides
- \(δ\)disque
- un disque ouvert dont le rayon est\(δ\) centré sur un point\((a,b)\)
- \(δ\)balle
- tous les points\(\mathbb{R}^3\) situés à une distance inférieure\(δ\) à\((x_0,y_0,z_0)\)
- point intérieur
- un point\(P_0\) de\(\mathbb{R}\) est un point limite s'il existe un\(δ\) disque centré autour duquel il est entièrement\(P_0\) contenu dans\(\mathbb{R}\)
- ensemble ouvert
- un ensemble\(S\) qui ne contient aucun de ses points limites
- région
- un sous-ensemble ouvert, connecté et non vide de\(\mathbb{R}^2\)


