14.1E : Exercices pour la section 14.1

Last updated
Save as PDF

Page ID: 197380

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Pour les exercices suivants, évaluez chaque fonction aux valeurs indiquées.

1)$ W(x,y)=4x^2+y^2.$ Trouvez$ W(2,−1), W(−3,6)$.

Réponse: $ W(2,−1) = 17,\quad W(−3,6) = 72$

2)$ W(x,y)=4x^2+y^2$. Trouvez$ W(2+h,3+h).$

3) Le volume d'un cylindre circulaire droit est calculé par une fonction de deux variables,$ V(x,y)=πx^2y,$ où$ x$ est le rayon du cylindre circulaire droit et$ y$ représente la hauteur du cylindre. Évaluez$ V(2,5)$ et expliquez ce que cela signifie.

Réponse: $ V(2,5) = 20π\,\text{units}^3$Il s'agit du volume lorsque le rayon est$ 2$ et la hauteur est$ 5$.

4) Un réservoir d'oxygène est constitué d'un cylindre droit de hauteur$ y$ et de rayon$ x$ avec deux hémisphères de rayon$ x$ montés en haut et en bas du cylindre. Exprimez le volume du cylindre en fonction de deux variables$ y$,$ x$ puis trouvez$ V(10,2)$ et expliquez ce que cela signifie.

Pour les exercices 5 à 10, trouvez le domaine et l'étendue de la fonction donnée. Indiquez le domaine en notation setbuilder et la plage en notation par intervalles.

5)$ V(x,y)=4x^2+y^2$

Réponse: Domaine :$\big\{(x, y) \, | \, x \in \rm I\!R, y \in \rm I\!R\big\}$ c'est-à-dire tous les points de la
plage$xy$ -plane :$ [0, \infty) $

6)$ f(x,y)=\sqrt{x^2+y^2−4}$

Réponse: Domaine :$ \big\{(x, y) \, | \, x^2+y^2 \ge 4\big\}$
Gamme :$ [0, \infty) $

7)$ f(x,y)=4\ln(y^2−x)$

Réponse: Domaine :$ \big\{(x, y) \, | \, x<y^2 \big\}$
Gamme :$ (-\infty, \infty) $

8)$ g(x,y)=\sqrt{16−4x^2−y^2}$

Réponse: Domaine :$ \big\{(x, y) \, | \, \dfrac{x^2}{4} + \dfrac{y^2}{16} \le 1\big\}$
Gamme :$ [0, 4] $

9)$ z=\arccos(y−x)$

Réponse: Domaine :$ \big\{(x, y) \, | \, x - 1 \le y \le x + 1\big\}$ c'est-à-dire tous les points situés entre les graphes de$y = x -1$ et$y = x +1 $.
Gamme :$ [0, \pi] $

10)$ f(x,y)=\dfrac{y+2}{x^2}$

Réponse: Domaine :$ \big\{(x, y) \, | \, x\neq 0 \big\}$
Gamme :$ (-\infty, \infty) $

Déterminez l'éventail des fonctions.

11)$ g(x,y)=\sqrt{16−4x^2−y^2}$

Réponse: $ \big\{z \, | \, 0≤z≤4\big\}$ou en notation par intervalles :$[0,4]$

(12)$ V(x,y)=4x^2+y^2$

(13)$ z=y^2−x^2$

Réponse: L'ensemble$\rm I\!R$

Dans les exercices 14 à 29, trouvez les courbes de niveau de chaque fonction aux valeurs indiquées$ c$ pour visualiser la fonction donnée. Esquissez un diagramme de contour pour les exercices où l'on vous demande plus de 3 valeurs de$c$.

(14)$ z(x,y)=y^2−x^2, \quad c=1$

(15)$ z(x,y)=y^2−x^2,\quad c=4$

Réponse: $ y^2−x^2=4,$une hyperbole

16)$ g(x,y)=x^2+y^2;\quad c=0, 1, 2, 3, 4, 9$

17)$ g(x,y)=4−x−y;\quad c=0,1, 2, 3, 4$

Réponse: Les courbes de niveau sont des lignes avec$ y = -x + (4 - c) $.
Pour chaque valeur,$c$ il y a :
$ c = 0: \, y = -x + 4$,
$ c = 1: \, y = -x + 3$,
$ c = 2: \, y = -x + 2$,
$ c = 3: \, y = -x + 1$,
$ c = 4: \, y = -x $.
Le diagramme de contour est constitué d'une série de lignes parallèles.
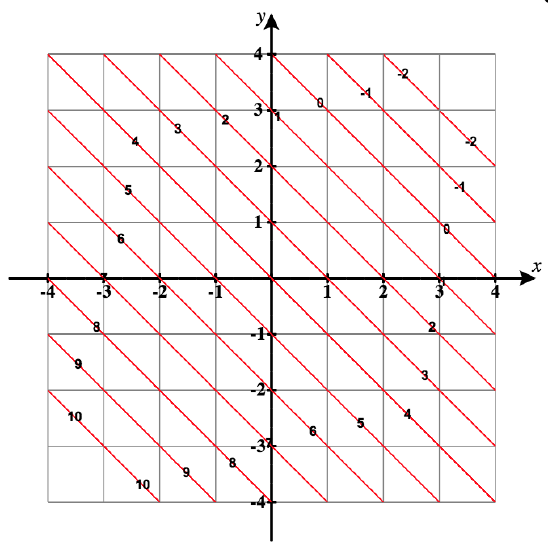
$Diagramme de contour de la fonction g (x, y) =4−x−y$

18)$ f(x,y)=xy;c=1;\quad c=−1$

19)$ h(x,y)=2x−y;\quad c=-2,0,2$

Réponse: $ 2x−y=0,2x−y=−2,2x−y=2;$trois lignes

(20)$ f(x,y)=x^2−y;\quad c=1,2$

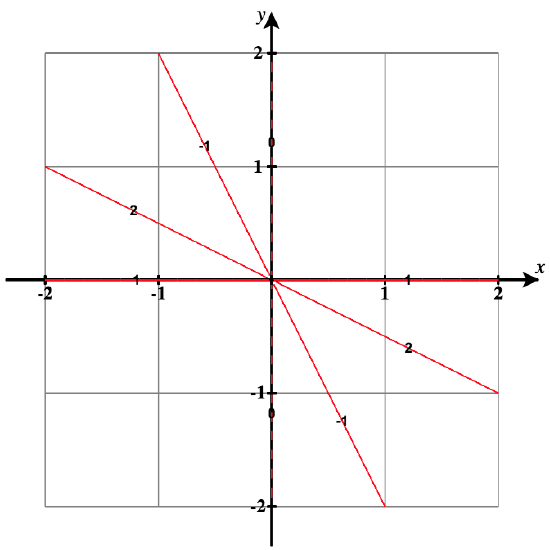
(21)$ g(x,y)=\dfrac{x}{x+y};c=−1,0,1,2$

Réponse: Les courbes de niveau sont des lignes avec la forme$ y = x \left( \dfrac{1-c}{c} \right) $. À$c = 0$, nous le résolvons directement à partir de l'équation$\dfrac{x}{x+y}=0$ pour obtenir$x = 0$.
Pour chaque valeur,$c$ il y a :
$ c = -1: \, y = -2x$,
$ c = 0: \, x = 0,\text{ with }y \ne 0$,
$ c = 1: \, y = 0,\text{ with }x \ne 0$,
$ c = 2: \, y = -\frac{1}{2}x$.
$Diagramme de contour de la fonction g (x, y) = x/ (x+y)$

(22)$ g(x,y)=x^3−y;\quad c=−1,0,2$

23)$ g(x,y)=e^{xy};\quad c=\frac{1}{2},3$

Réponse: Les courbes de niveau ont la forme,$ y = \dfrac{\ln c}{x}$.
Pour chaque valeur,$c$ il y
$ c = \frac{1}{2}: \, y = \dfrac{\ln \frac{1}{2}}{x}$ a : qui peut être réécrit comme,$y = -\dfrac{\ln 2}{x}$

$ c = 3: \, y = \dfrac{\ln 3}{x}$.

(24)$ f(x,y)=x^2;\quad c=4,9$

25)$ f(x,y)=xy−x;\quad c=−2,0,2$

Réponse: Les courbes de niveau ont la forme :$ y = \dfrac{c}{x} + 1$.
Ici$y = \dfrac{-2}{x} + 1,\quad y = 1,\quad y = \dfrac{2}{x} + 1$ ou$ xy−x=−2,\,xy−x=0,\,xy−x=2$

(26)$ h(x,y)=\ln(x^2+y^2);\quad c=−1,0,1$

(27)$ g(x,y)=\ln\left(\dfrac{y}{x^2}\right);\quad c=−2,0,2$

Réponse: Les courbes de niveau ont la forme,$ y =e^c x^2$.
Pour chaque valeur, il$c$ y a :
$ c = -2: \, y = e^{-2} x^2 $,
$ c = 0: \, y = x^2 $,
$ c = 2: \, y = e^{2} x^2 $.

(28)$ z=f(x,y)=\sqrt{x^2+y^2},\quad c=3$

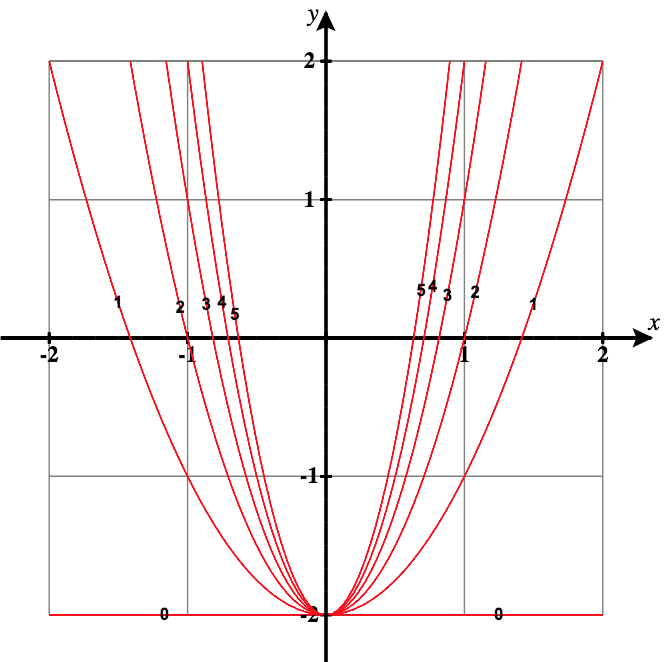
29)$ f(x,y)=\dfrac{y+2}{x^2},\quad c=$ toute constante

Réponse: Les courbes de niveau sont des paraboles de la forme$ y=cx^2−2,\text{ with }x \ne 0$.
$Diagramme de contour de la fonction f (x, y) = (y + 2) /x^2$

Dans les exercices 30 à 32, trouvez les traces verticales des fonctions aux valeurs indiquées de$ x$ et$ y$, puis tracez les traces.

(30)$ z=4−x−y, \quad x=2$

31)$ f(x,y)=3x+y^3, \quad x=1$

Réponse

$ z=3+y^3,$une courbe dans le $zy$plan avec des règles parallèles à l'$x$axe

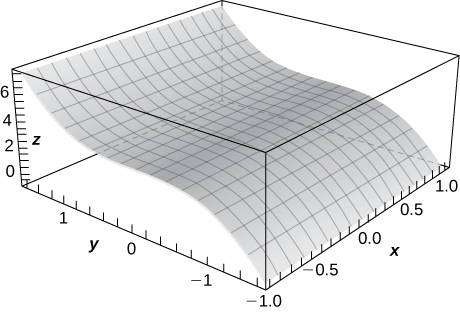
$Diagramme de surface de la fonction f (x, y) =3x+y^3$

32)$ z=\cos\sqrt{x^2+y^2}, \quad x=1$

Dans les exercices 33 à 38, déterminez le domaine et l'étendue de chaque fonction.

33)$ z=\sqrt{100−4x^2−25y^2}$

Réponse: Domaine :$ \big\{(x, y) \, | \, \dfrac{x^2}{25}+\dfrac{y^2}{4}≤1\big\}$
Gamme :$ [0, 10] $

34)$ z=\ln(x−y^2)$

35)$ f(x,y,z)=\dfrac{1}{\sqrt{36−4x^2−9y^2−z^2}}$

Réponse: Domaine :$ \big\{(x, y, z) \, | \, \dfrac{x^2}{9}+\dfrac{y^2}{4}+\dfrac{z^2}{36}<1\big\}$
Gamme :$ \big[\frac{1}{6}, \infty\big) $

36)$ f(x,y,z)=\sqrt{49−x^2−y^2−z^2}$

(37)$ f(x,y,z)=\sqrt[3]{16−x^2−y^2−z^2}$

Réponse: Domaine : Tous les points de$ xyz$ l'espace
Plage :$ \big(-\infty, \sqrt[3]{16}\,\big] $

38)$ f(x,y)=\cos\sqrt{x^2+y^2}$

Dans les exercices 39 à 40, tracez un graphique de la fonction.

39)$ z=f(x,y)=\sqrt{x^2+y^2}$

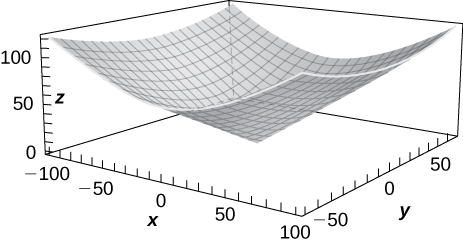
Réponse: $Tracé de la surface f (x, y) =sqrt (x^2+y^2)$

40)$ z=x^2+y^2$

41) Utiliser la technologie pour représenter graphiquement$ z=x^2y.$

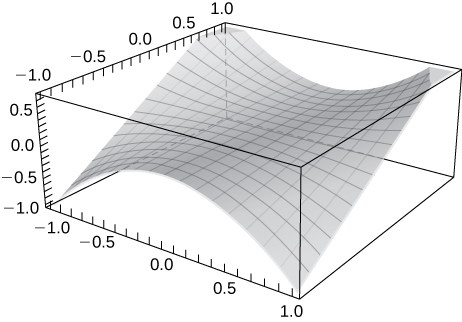
Réponse: $Diagramme de surface de la fonction z=x^2y$

Dans les exercices 42 à 46, esquissez la fonction en trouvant ses courbes de niveau. Vérifiez le graphique à l'aide d'une technologie telle que CalcPlot3D.

(42)$ f(x,y)=\sqrt{4−x^2−y^2}$

43)$ f(x,y)=2−\sqrt{x^2+y^2}$

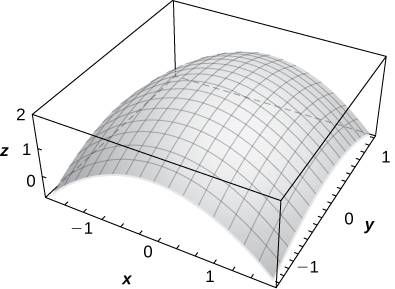
Réponse: $Diagramme de surface de la fonction f (x, y) =2−sqrt (x^2+y^2)$

44)$ z=1+e^{−x^2−y^2}$

45)$ z=\cos\sqrt{x^2+y^2}$

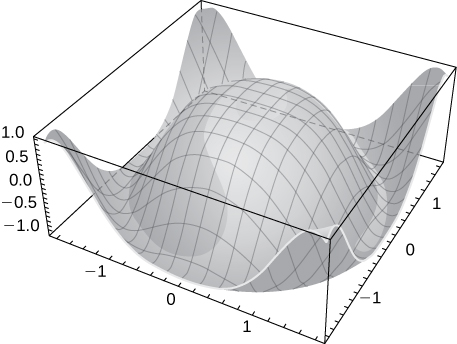
Réponse: $Diagramme de surface de la fonction z=cos (sqrt (x^2+y^2))$

46)$ z=y^2−x^2$

47) Décrivez les lignes de contour pour plusieurs valeurs de$ c$ pour$ z=x^2+y^2−2x−2y.$

Réponse: Les lignes de contour sont des cercles concentriques centrés sur le point,$ (1, 1) $.
Vous pouvez le voir en complétant le carré après avoir défini cette fonction sur$c$.
C'est-à-dire que nous écrivons$ x^2-2x+1+y^2−2y+1 = c + 2 $ ce qui peut être réécrit comme,$ (x - 1)^2 + (y - 1)^2 = c + 2 $.
Cela nous donne des cercles centrés sur le point$ (1, 1) $, chacun avec un rayon de$ \sqrt{c+2} $.

Dans les exercices 48 à 52, trouvez la surface plane pour la valeur donnée de$c$ pour chaque fonction de trois variables et décrivez-la.

48)$ w(x,y,z)=x−2y+z,\quad c=4$

49)$ w(x,y,z)=x^2+y^2+z^2,\quad c=9$

Réponse: $ x^2+y^2+z^2=9$, une sphère de rayon$ 3$

50)$ w(x,y,z)=x^2+y^2−z^2,\quad c=−4$

51)$ w(x,y,z)=x^2+y^2−z^2,\quad c=4$

Réponse: $ x^2+y^2−z^2=4,$un hyperboloïde d'une feuille

52)$ w(x,y,z)=9x^2−4y^2+36z^2,\quad c=0$

Dans les exercices 53 à 55, trouvez une équation de la courbe de niveau$ f$ contenant le point$ P$.

53)$ f(x,y)=1−4x^2−y^2,\quad P(0,1)$

Réponse: $ 4x^2+y^2=1,$

(54)$ g(x,y)=y^2\arctan x,\quad P(1,2)$

55)$ g(x,y)=e^{xy}(x^2+y^2),\quad P(1,0)$

Réponse: $ 1=e^{xy}(x^2+y^2)$

56) L'intensité$ E$ d'un champ électrique au point$ (x,y,z)$ résultant d'un fil chargé infiniment long situé le long de l'$y$axe y est donnée par$ E(x,y,z)=k/\sqrt{x^2+y^2}$, où$ k$ est une constante positive. Pour plus de simplicité$ k=1$, imaginez les équations des surfaces planes pour$ E=10$ et$ E=100.$

57) Une fine plaque en fer est située dans le$xy$ plan. La température$ T$ en degrés Celsius en un point$ P(x,y)$ est inversement proportionnelle au carré de sa distance par rapport à l'origine. Exprimer$ T$ en fonction de$ x$ et$ y$.

Réponse: $ T(x,y)=\dfrac{k}{x^2+y^2}$

58) Reportez-vous au problème précédent. À l'aide de la fonction de température qui s'y trouve, déterminez la constante de proportionnalité si la température au point$ P(1,2)$ est$ 50°C.$ Utiliser cette constante pour déterminer la température au point$ Q(3,4).$

59) Reportez-vous au problème précédent. Trouvez les courbes de niveau pour$ T=40°C$$ T=100°C,$ et décrivez ce que les courbes de niveau représentent.

Réponse: $ x^2+y^2=\dfrac{k}{40}, \quad x^2+y^2=\dfrac{k}{100}$. Les courbes de niveau représentent des cercles de rayons$ \sqrt{10k}/20$ et$ \sqrt{k}/10$

Contributeurs

Template:ContribOpenStaxCalc
Paul Seeburger (Monroe Community College) added the contour plots to answers for problems 17, 21 and 29.