14.1 : Fonctions de plusieurs variables

Objectifs d'apprentissage

• Reconnaissez une fonction composée de deux variables et identifiez son domaine et sa plage.
• Esquissez un graphe d'une fonction de deux variables.
• Esquissez plusieurs traces ou courbes de niveau d'une fonction de deux variables.
• Reconnaissez une fonction composée de trois variables ou plus et identifiez ses surfaces planes.

Notre première étape consiste à expliquer ce qu'est une fonction de plusieurs variables, en commençant par les fonctions de deux variables indépendantes. Cette étape consiste à identifier le domaine et la gamme de ces fonctions et à apprendre à les représenter graphiquement. Nous examinons également les moyens de relier les graphes de fonctions en trois dimensions à des graphes de fonctions planaires plus familières.

Fonctions de deux variables

La définition d'une fonction de deux variables est très similaire à celle d'une fonction d'une seule variable. La principale différence est qu'au lieu de mapper les valeurs d'une variable avec les valeurs d'une autre variable, nous mappons des paires ordonnées de variables vers une autre variable.

Définition : fonction de deux variables

Une fonction de deux variables fait\(z=f(x,y)\) correspondre chaque paire\((x,y)\) ordonnée d'un sous-ensemble\(D\) du plan réel\(R^2\) à un nombre réel z unique. L'ensemble\(D\) est appelé le domaine de la fonction. La plage de\(f\) est l'ensemble de tous les nombres réels z qui ont au moins une paire ordonnée,\((x,y)∈D\)\(f(x,y)=z\) comme indiqué sur la figure\(\PageIndex{1}\).

Figure\(\PageIndex{1}\) : Le domaine d'une fonction à deux variables est constitué de paires ordonnées\((x,y)\).

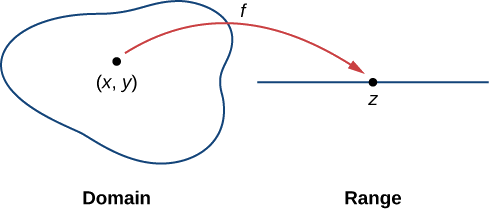
La détermination du domaine d'une fonction à deux variables implique de prendre en compte toutes les restrictions de domaine qui peuvent exister. Jetons un coup d'œil.

Exemple\(\PageIndex{1}\): Domains and Ranges for Functions of Two Variables

Trouvez le domaine et la plage de chacune des fonctions suivantes :

1. \(f(x,y)=3x+5y+2\)
2. \(g(x,y)=\sqrt{9−x^2−y^2}\)

Solution

a. Voici un exemple de fonction linéaire à deux variables. Il n'y a pas de valeurs ou de combinaisons de\(x\) et\(y\) qui peuvent être indéfinies, donc le domaine de\(f\) est\(R^2\).\(f(x,y)\) Pour déterminer la plage, choisissez d'abord une valeur pour z. Nous devons trouver une solution à l'équation\(f(x,y)=z,\) ou\(3x−5y+2=z.\) une telle solution peut être obtenue en réglant d'abord\(y=0\), ce qui donne l'équation\(3x+2=z\). La solution de cette équation est\(x=\dfrac{z−2}{3}\), qui donne la paire ordonnée\(\left(\dfrac{z−2}{3},0\right)\) comme solution à l'équation\(f(x,y)=z\) pour n'importe quelle valeur de\(z\). Par conséquent, la plage de la fonction est composée uniquement de nombres réels, ou\(R\).

b. Pour que la fonction\(g(x,y)\) ait une valeur réelle, la quantité sous la racine carrée doit être non négative :

\[ 9−x^2−y^2≥0. \nonumber \]

Cette inégalité peut être écrite sous la forme

\[ x^2+y^2≤9. \nonumber \]

Par conséquent, le domaine de\(g(x,y)\) est\(\{(x,y)∈R^2∣x^2+y^2≤9\}\). Le graphe de cet ensemble de points peut être décrit comme un disque de rayon 3 centré à l'origine. Le domaine inclut le cercle de délimitation, comme indiqué dans le graphique suivant.

Figure\(\PageIndex{2}\) : Le domaine de la fonction\(g(x,y)=\sqrt{9−x^2−y^2}\) est un disque fermé de rayon 3.

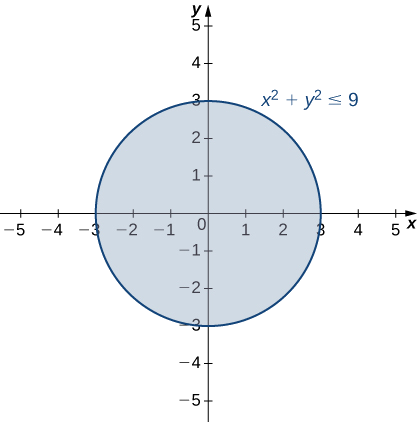
Pour déterminer la plage de,\(g(x,y)=\sqrt{9−x^2−y^2}\) nous commençons par un point situé\((x_0,y_0)\) à la limite du domaine, qui est défini par la relation\(x^2+y^2=9\). Il s'ensuit que\(x^2_0+y^2_0=9\) et

\[ \begin{align*} g(x_0,y_0) =\sqrt{9−x^2_0−y^2_0} \\[4pt] =\sqrt{9−(x^2_0+y^2_0)}\\[4pt] =\sqrt{9−9}\\[4pt] =0. \end{align*}\]

Si\(x^2_0+y^2_0=0\) (en d'autres termes\(x_0=y_0=0)\), alors

\[ \begin{align*} g(x_0,y_0) =\sqrt{9−x^2_0−y^2_0}\\[4pt] =\sqrt{9−(x^2_0+y^2_0)}\\[4pt] =\sqrt{9−0}=3. \end{align*}\]

Il s'agit de la valeur maximale de la fonction. Étant donné n'importe quelle valeur\(c\) comprise entre\(0\) et\(3\), nous pouvons trouver un ensemble complet de points dans le domaine de\(g\) tel que\(g(x,y)=c:\)

\[\begin{align*} \sqrt{9−x^2−y^2} =c \\[4pt] 9−x^2−y^2 =c^2 \\[4pt] x^2+y^2 =9−c^2. \end{align*}\]

Puisque\(9−c^2>0\), cela décrit un cercle de rayon\(\sqrt{9−c^2}\) centré à l'origine. Tout point de ce cercle répond à l'équation\(g(x,y)=c\). Par conséquent, la plage de cette fonction peut être écrite en notation par intervalles sous la forme\([0,3].\)

Exercice\(\PageIndex{1}\)

Déterminez le domaine et la plage de la fonction\(f(x,y)=\sqrt{36−9x^2−9y^2}\).

Allusion

Déterminez l'ensemble des paires ordonnées qui ne rendent pas le radical et le négatif.

Solution

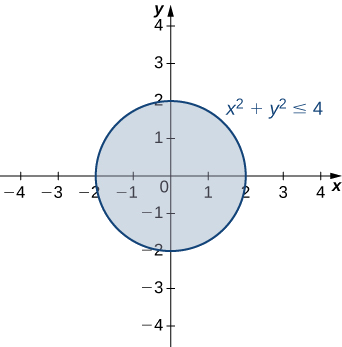
Le domaine est\(\{(x, y) | x^2+y^2≤4 \}\) le cercle ombré défini par l'inégalité\(x^2+y^2≤4\), dont la limite est un cercle\(2\) de rayon. La gamme est\([0,6].\)

Fonctions graphiques de deux variables

Supposons que nous souhaitions représenter graphiquement la fonction.\(z=f(x,y).\) Cette fonction possède deux variables indépendantes (\(x\)et\(y\)) et une variable dépendante\((z)\). Pour représenter graphiquement\(y=f(x)\) la fonction d'une variable, nous utilisons le plan cartésien. Nous sommes en mesure de représenter graphiquement n'importe quelle paire ordonnée\((x,y)\) dans le plan, et chaque point du plan est\((x,y)\) associée à une paire ordonnée. Avec une fonction de deux variables, chaque paire ordonnée\((x,y)\) dans le domaine de la fonction est mappée à un nombre réel\(z\). Par conséquent, le graphe de la fonction\(f\) est constitué de triples ordonnés\((x,y,z)\). Le graphe d'une fonction\(z=f(x,y)\) de deux variables est appelé surface.

Pour mieux comprendre le concept qui consiste à tracer un ensemble de triples ordonnés pour obtenir une surface dans un espace tridimensionnel, imaginez que le système de\((x,y)\) coordonnées soit plat. Ensuite, chaque point du domaine de la fonction f est associé à une\(z\) valeur unique. S'il\(z\) est positif, alors le point graphique est situé au-dessus du\(xy\) plan, s'il\(z\) est négatif, alors le point graphique est situé en dessous du\(xy\) plan. L'ensemble de tous les points représentés sur le graphique devient la surface bidimensionnelle qui est le graphe de la fonction\(f\).

Exemple\(\PageIndex{2}\): Graphing Functions of Two Variables

Créez un graphique de chacune des fonctions suivantes :

1. \(g(x,y)=\sqrt{9−x^2−y^2}\)
2. \(f(x,y)=x^2+y^2\)

Solution

a. Dans l'exemple\(\PageIndex{2}\), nous avons déterminé que le domaine de\(g(x,y)=\sqrt{9−x^2−y^2}\) est\(\{(x,y)∈R^2∣x^2+y^2≤9\}\) et que la plage est\(\{z∈R^2∣0≤z≤3\}\). Quand\(x^2+y^2=9\) nous l'aurons fait\(g(x,y)=0\). Par conséquent, tout point du cercle de rayon\(3\) centré à l'origine dans le\(xy\) plan -plane correspond à\(z=0\) in\(R^3\). Si\(g(x,y)=1,\) c'est le cas\(x^2+y^2=8\), tout point du cercle de rayon\(2\sqrt{2}\) centré à l'origine dans le\(xy\) plan -plane correspond à\(z=1\) in\(R^3\). Au\(x^2+y^2\) fur et à mesure que l'on se rapproche de zéro, la valeur des\(z\) approches\(3\) Quand\(x^2+y^2=0\), alors\(g(x,y)=3\). Il s'agit de l'origine dans le\(xy\) plan. Si\(x^2+y^2\) est égal à toute autre valeur comprise entre\(0\) et\(9\), alors\(g(x,y)\) est égal à une autre constante comprise entre\(0\) et\(3\). La surface décrite par cette fonction est un hémisphère centré à l'origine avec un rayon,\(3\) comme le montre le graphique suivant.

Figure\(\PageIndex{3}\) : Graphique de l'hémisphère représenté par la fonction donnée de deux variables.

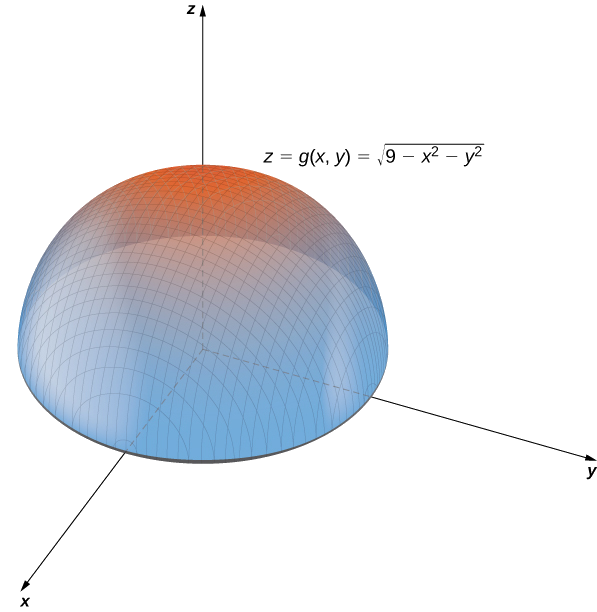
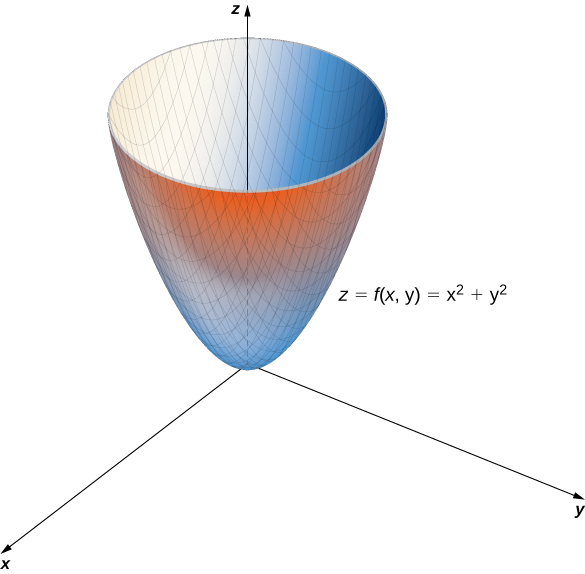
b. Cette fonction contient également l'expression\(x^2+y^2\). En fixant cette expression à différentes valeurs commençant à zéro, nous obtenons des cercles de rayon croissant. La valeur minimale de\(f(x,y)=x^2+y^2\) est zéro (atteinte lorsque\(x=y=0.\). Quand\(x=0\), la fonction devient\(z=y^2\), et quand\(y=0\), alors la fonction devient\(z=x^2\). Ce sont des coupes transversales du graphique et des paraboles. Rappelons dans Introduction aux vecteurs dans l'espace que le nom du graphe\(f(x,y)=x^2+y^2\) est un paraboloïde. Le graphique de\(f\) apparaît dans le graphique suivant.

Figure\(\PageIndex{4}\) : Un paraboloïde est le graphe de la fonction donnée de deux variables.

Exemple\(\PageIndex{3}\): Nuts and Bolts

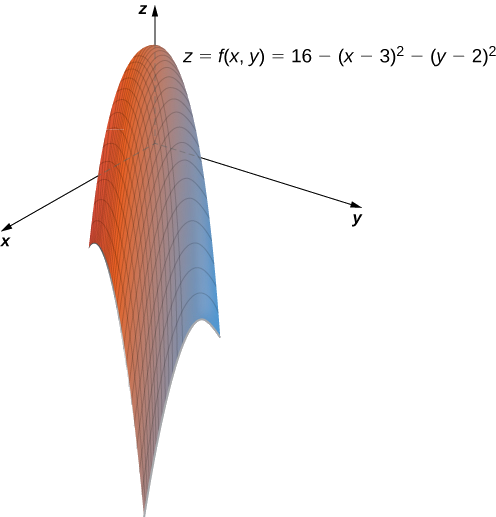
Une fonction de profit pour un fabricant de matériel est donnée par

\[f(x,y)=16−(x−3)^2−(y−2)^2, \nonumber \]

où\(x\) est le nombre d'écrous vendus par mois (mesuré en milliers) et\(y\) représente le nombre de boulons vendus par mois (mesuré en milliers). Le profit est mesuré en milliers de dollars. Esquissez un graphique de cette fonction.

Solution

Cette fonction est une fonction polynomiale composée de deux variables. Le domaine de\(f\) se compose de paires de\((x,y)\) coordonnées qui génèrent un profit non négatif :

\[ \begin{align*} 16−(x−3)^2−(y−2)^2 ≥ 0 \\[4pt] (x−3)^2+(y−2)^2 ≤ 16. \end{align*}\]

Il s'agit d'un disque dont le rayon est\(4\) centré sur\((3,2)\). Une autre restriction est que les deux\(x\) et\(y\) doivent être non négatifs. Quand\(x=3\) et\(y=2, f(x,y)=16.\) Notez qu'il est possible que l'une ou l'autre valeur ne soit pas un entier ; par exemple, il est possible de vendre des\(2.5\) milliers de noix par mois. Le domaine contient donc des milliers de points, ce qui nous permet de prendre en compte tous les points du disque. Pour tout\(z<16\), nous pouvons résoudre l'équation\(f(x,y)=16:\)

\[ \begin{align*} 16−(x−3)^2−(y−2)^2 =z \\[4pt] (x−3)^2+(y−2)^2 =16−z. \end{align*}\]

Puisque\(z<16,\) nous le savons\(16−z>0,\), l'équation précédente décrit un cercle dont le rayon est\(\sqrt{16−z}\) centré sur le point\((3,2)\). Par conséquent, la plage de\(f(x,y)\) est\(\{z∈\mathbb{R}|z≤16\}.\) Le graphique de\(f(x,y)\) est également un paraboloïde, et ce paraboloïde pointe vers le bas, comme indiqué.

Figure\(\PageIndex{5}\) : Le graphique de la fonction donnée de deux variables est également un paraboloïde.

Courbes de niveau

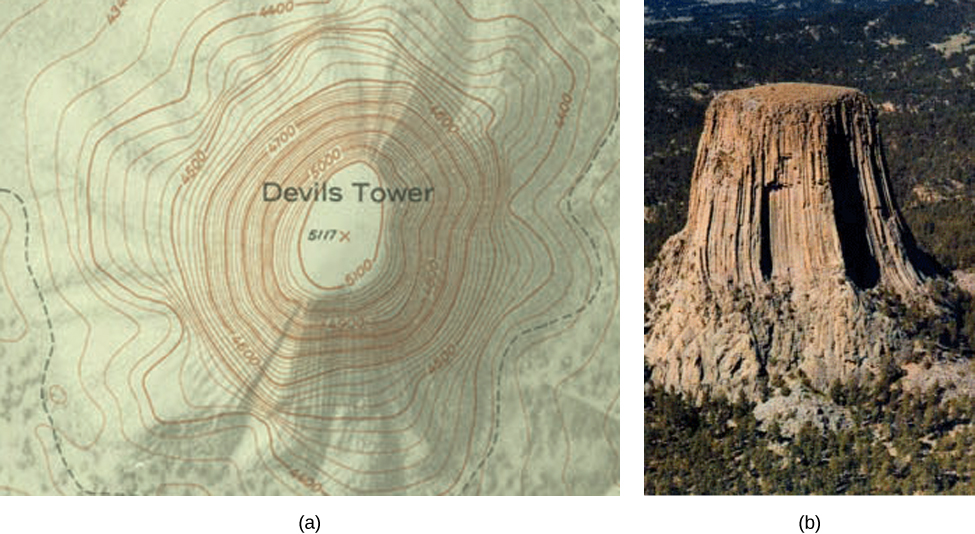
Si les randonneurs empruntent des sentiers accidentés, ils peuvent utiliser une carte topographique qui indique l'inclinaison des sentiers. Une carte topographique contient des lignes courbes appelées lignes de contour. Chaque ligne de contour correspond aux points de la carte qui ont la même altitude (Figure\(\PageIndex{6}\)). Une courbe de niveau d'une fonction de deux variables\(f(x,y)\) est complètement analogue à une ligne de contour sur une carte topographique.

Figure\(\PageIndex{6}\) : (a) Une carte topographique de Devil's Tower, dans le Wyoming. Des lignes rapprochées indiquent un terrain très escarpé. (b) Une photo en perspective de la Devil's Tower montre à quel point ses flancs sont raides. Remarquez que le sommet de la tour a la même forme que le centre de la carte topographique.

Définition : courbes de niveau

Étant donné une fonction\(f(x,y)\) et un nombre compris\(c\) dans la plage de\(f\), une courbe de niveau d'une fonction de deux variables pour la valeur\(c\) est définie comme étant l'ensemble des points satisfaisant l'équation\(f(x,y)=c.\)

Pour en revenir à la fonction\(g(x,y)=\sqrt{9−x^2−y^2}\), nous pouvons déterminer les courbes de niveau de cette fonction. La plage de\(g\) est l'intervalle fermé\([0,3]\). Tout d'abord, nous choisissons n'importe quel nombre dans cet intervalle fermé, disons,\(c=2\). La courbe de niveau correspondant à\(c=2\) est décrite par l'équation

\[ \sqrt{9−x^2−y^2}=2. \nonumber \]

Pour simplifier, mettez les deux côtés de cette équation au carré :

\[ 9−x^2−y^2=4. \nonumber \]

Maintenant, multipliez les deux côtés de l'équation par\(−1\) et ajoutez\(9\) à chaque côté :

\[ x^2+y^2=5. \nonumber \]

Cette équation décrit un cercle centré à l'origine avec un rayon\(\sqrt{5}\). L'utilisation de valeurs comprises\(c\) entre\(0\) et\(3\) permet d'obtenir d'autres cercles également centrés sur l'origine. Si\(c=3\), alors le cercle a un rayon\(0\), il se compose donc uniquement de l'origine. La figure\(\PageIndex{7}\) est un graphique des courbes de niveau de cette fonction correspondant à\(c=0,1,2,\) et\(3\). Notez que dans la dérivation précédente, il est possible que nous ayons introduit des solutions supplémentaires en mettant les deux côtés au carré. Ce n'est pas le cas ici car la plage de la fonction de racine carrée n'est pas négative.

Figure\(\PageIndex{7}\) : Courbes de niveau de la fonction\(g(x,y)=\sqrt{9−x^2−y^2}\) (utilisant\(c=0,1,2,\) et\(3 (c=3\) correspondant à l'origine).

Un graphe des différentes courbes de niveau d'une fonction est appelé carte de contour.

Exemple\(\PageIndex{4}\): Making a Contour Map

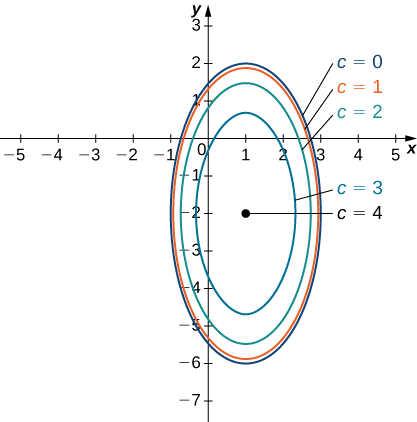
\(f(x,y)=\sqrt{8+8x−4y−4x^2−y^2}\)En fonction de la fonction, trouvez la courbe de niveau correspondant à\(c=0\). Créez ensuite une carte de contours pour cette fonction. Quels sont le domaine et l'étendue de\(f\) ?

Solution

Pour trouver la courbe de niveau,\(c=0,\) nous la définissons\(f(x,y)=0\) et la résolvons. Cela donne

\(0=\sqrt{8+8x−4y−4x^2−y^2}\).

On met ensuite les deux côtés au carré et on multiplie les deux côtés de l'équation par\(−1\) :

\(4x^2+y^2−8x+4y−8=0.\)

Maintenant, nous réorganisons les termes, les\(x\) assemblons et les\(y\) termes, et ajoutons\(8\) à chaque côté :

\(4x^2−8x+y^2+4y=8.\)

Ensuite, nous regroupons les paires de termes contenant la même variable entre parenthèses, et les factorisons\(4\) à partir de la première paire :

\(4(x^2−2x)+(y^2+4y)=8.\)

Ensuite, nous complétons le carré entre chaque paire de parenthèses et ajoutons la valeur correcte sur le côté droit :

\(4(x^2−2x+1)+(y^2+4y+4)=8+4(1)+4.\)

Ensuite, on prend en compte le côté gauche et on simplifie le côté droit :

\(4(x−1)^2+(y+2)^2=16.\)

Enfin, nous divisons les deux côtés par\(16:\)

\(\dfrac{(x−1)^2}{4}+\dfrac{(y+2)^2}{16}=1.\label{conteq0}\)

Cette équation décrit une ellipse centrée sur\((1,−2).\) Le graphique de cette ellipse apparaît dans le graphique suivant.

Figure\(\PageIndex{8}\) : Courbe de niveau de la fonction\(f(x,y)=\sqrt{8+8x−4y−4x^2−y^2}\) correspondant à\(c=0\)

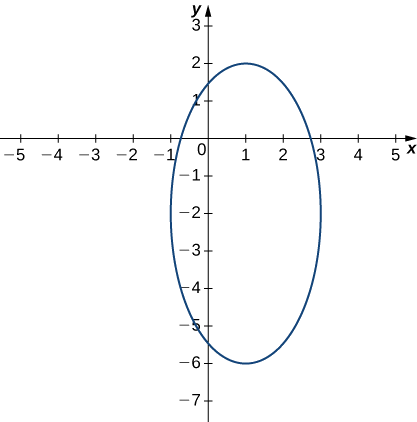
Nous pouvons répéter la même dérivation pour des valeurs\(c\) inférieures à\(4.\) Alors, l'équation \ ref {conteq0} devient

\(\dfrac{4(x−1)^2}{16−c^2}+\dfrac{(y+2)^2}{16−c^2}=1\)

pour une valeur arbitraire de\(c\). La figure\(\PageIndex{9}\) montre une carte de contour permettant\(f(x,y)\) d'utiliser les valeurs\(c=0,1,2,\) et\(3\). Lorsque\(c=4,\) la courbe de niveau est le point\((−1,2)\).

Figure\(\PageIndex{9}\) : Carte des contours de la fonction\(f(x,y)=\sqrt{8+8x−4y−4x^2−y^2}\) utilisant les valeurs\(c=0,1,2,3,\) et\(4\).

Trouver le domaine et la gamme

Comme il s'agit d'une fonction de racine carrée, le radical ne doit pas être négatif. Nous avons donc

\[8+8x−4y−4x^2−y^2\ge 0 \nonumber \]

Reconnaissant que la limite du domaine est une ellipse, nous répétons les étapes que nous avons montrées ci-dessus pour obtenir

\[\dfrac{(x−1)^2}{4}+\dfrac{(y+2)^2}{16}\le 1 \nonumber \]

Ainsi, le domaine de\(f\) peut être écrit :\(\big\{ (x,y) \,|\, \frac{(x−1)^2}{4}+\frac{(y+2)^2}{16}\le 1 \big\}.\)

Pour trouver la plage de,\(f,\) nous devons prendre en compte les sorties possibles de cette fonction de racine carrée. Nous savons que la sortie ne peut pas être négative, nous devons donc vérifier ensuite si sa sortie est\(0.\) issue du travail que nous avons effectué ci-dessus pour trouver la courbe de niveau, car\(c = 0,\) nous savons que la valeur de\(f\) est\(0\) pour n'importe quel point de cette courbe de niveau (sur l'ellipse\(\frac{(x−1)^2}{4}+\frac{(y+2)^2}{16}=1\)). Nous savons donc que la limite inférieure de la plage de cette fonction est\(0.\)

Pour déterminer la limite supérieure de la plage de la fonction dans ce problème, il est plus facile de compléter d'abord le carré sous le radical.

\ [\ begin {align*} f (x, y) &= \ sqrt {8+8x−4y−4x^2−y^2} \ \ [5 points]
&= \ sqrt {8 - 4 (x^2 - 2 x \ quad) - (y^2 + 4 ans \ quad)} \ \ [5 points] &= \ sqrt {8 - 4 (x^2 - 2x \ +1)} \ \ [5 points]
&= \ sqrt {8 - 4 (x^2 - 2 x - +1) 1) - (y^2 + 4y + 4 - 4)} \ \ [5 points]
&= \ sqrt {8 - 4 (x^2 - 2x +1) + 4 - (y^2 + 4 ans + 4) +4} \ \ [5 points]
&= \ sqrt {16 - 4 (x-1) ^2 - (y+2) ^2} \ end {align*} \]

Maintenant que nous l'avons\(f\) sous cette forme, nous pouvons voir la taille du radicand. Puisque nous soustrayons deux carrés parfaits,\(16,\) nous savons que la valeur du radicand ne peut pas être supérieure\(16.\) à Au point où\((1, -2),\) nous pouvons voir que le radicand sera de 16 (puisque nous allons\(0\) soustraire\(16\) à ce stade). Cela nous donne la valeur maximale de\(f\), c'est-à-dire\(f(1, -2) = \sqrt{16} = 4.\)

La plage de cette fonction est donc\([0, 4].\)

Exercice\(\PageIndex{2}\)

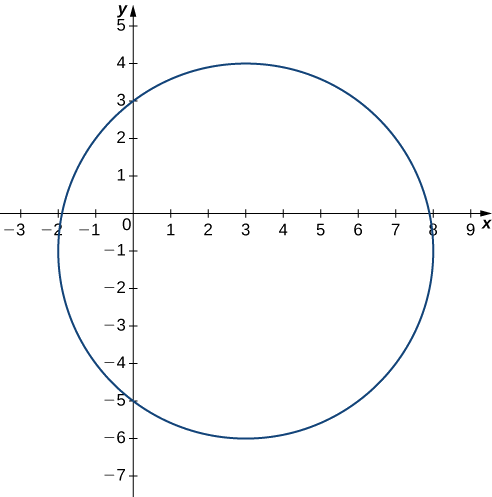
Trouvez et tracez la courbe de niveau de la fonction\(g(x,y)=x^2+y^2−6x+2y\) correspondant à\(c=15.\)

Allusion

Tout d'abord, définissez\(g(x,y)=15\) puis complétez le carré.

Solution

L'équation de la courbe de niveau peut être écrite comme étant un cercle\((x−3)^2+(y+1)^2=25,\) dont le rayon est\(5\) centré sur\((3,−1).\)

Un autre outil utile pour comprendre le graphe d'une fonction de deux variables est le traçage vertical. Les courbes de niveau sont toujours représentées graphiquement dans le\(xy-plane\), mais comme leur nom l'indique, les traces verticales sont représentées dans les\(yz\) plans\(xz\) - ou.

Définition : traces verticales

Prenons l'exemple d'une fonction\(z=f(x,y)\) avec domaine\(D⊆\mathbb{R}^2\). Une trace verticale de la fonction peut être soit l'ensemble de points qui résout l'équation\(f(a,y)=z\) pour une constante donnée,\(x=a\) soit\(f(x,b)=z\) pour une constante donnée\(y=b.\)

Exemple\(\PageIndex{5}\): Finding Vertical Traces

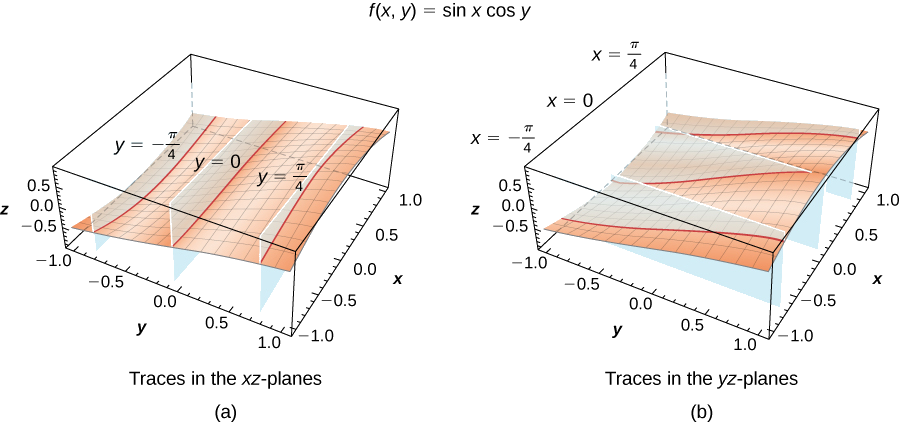
Trouvez des traces verticales pour la fonction\(f(x,y)=\sin x \cos y\) correspondant à\(x=−\dfrac{π}{4},0,\) et\(\dfrac{π}{4}\)\(y=−\dfrac{π}{4},0\), et\(\dfrac{π}{4}\).

Solution

Premier ensemble\(x=−\dfrac{π}{4}\) de l'équation\(z=\sin x \cos y:\)

\(z=\sin(−\dfrac{π}{4})\cos y=−\dfrac{\sqrt{2}\cos y}{2}≈−0.7071\cos y.\)

Cela décrit un graphe en cosinus dans le plan\(x=−\dfrac{π}{4}\). Les autres valeurs de z apparaissent dans le tableau suivant.

Traces verticales parallèles à la\(xz-Plane\) pour la fonction\(f(x,y)=\sin x \cos y\)

\(c\)	Vertical Trace pour\(x=c\)
\ (c \) » style="vertical-align:middle ; « >\(−\dfrac{π}{4}\)	\ (x=c \) » style="vertical-align:middle ; « >\(z=−\dfrac{\sqrt{2}\cos y}{2}\)
\ (c \) » style="vertical-align:middle ; « >0	\ (x=c \) » style="vertical-align:middle ; « >\(z=0\)
\ (c \) » style="vertical-align:middle ; « >\(\dfrac{π}{4}\)	\ (x=c \) » style="vertical-align:middle ; « >\(z=\dfrac{\sqrt{2}\cos y}{2}\)

De la même manière, nous pouvons remplacer le\(y-values\) dans l'équation\(f(x,y)\) pour obtenir les traces dans le\(yz-plane,\) comme indiqué dans le tableau suivant.

Traces verticales parallèles à la\(yz-Plane\) pour la fonction\(f(x,y)=\sin x \cos y\)

\(d\)	Vertical Trace pour\(y=d\)
\ (d \) » style="vertical-align:middle ; « >\(\dfrac{π}{4}\)	\ (y=d \) » style="vertical-align:middle ; « >\(z=\dfrac{\sqrt{2}\sin x}{2}\)
\ (d \) » style="vertical-align:middle ; « >0	\ (y=d \) » style="vertical-align:middle ; « >\(z=\sin x\)
\ (d \) » style="vertical-align:middle ; « >\(−\dfrac{π}{4}\)	\ (y=d \) » style="vertical-align:middle ; « >\(z=\dfrac{\sqrt{2}\sin x}{2}\)

Les trois traces du\(xz-plane\) sont des fonctions cosinus ; les trois traces du\(yz-plane\) sont des fonctions sinusoïdales. Ces courbes apparaissent aux intersections de la surface avec\(x=−\dfrac{π}{4},x=0,x=\dfrac{π}{4}\) les plans,\(y=−\dfrac{π}{4},y=0,y=\dfrac{π}{4}\) comme le montre la figure suivante.

Figure\(\PageIndex{10}\) : Les tracés verticaux de la fonction\(f(x,y)\) sont des courbes en cosinus dans le\(xz-planes\) (a) et des courbes sinusoïdales dans le\(yz-planes\) (b).

Exercice\(\PageIndex{3}\)

Déterminez l'équation du tracé vertical de la fonction\(g(x,y)=−x^2−y^2+2x+4y−1\) correspondant à\(y=3\) et décrivez son graphe.

Allusion

Définissez\(y=3\) l'équation\(z=−x^2−y^2+2x+4y−1\) et complétez le carré.

Solution

\(z=3−(x−1)^2\). Cette fonction décrit une parabole s'ouvrant vers le bas dans le plan\(y=3\).

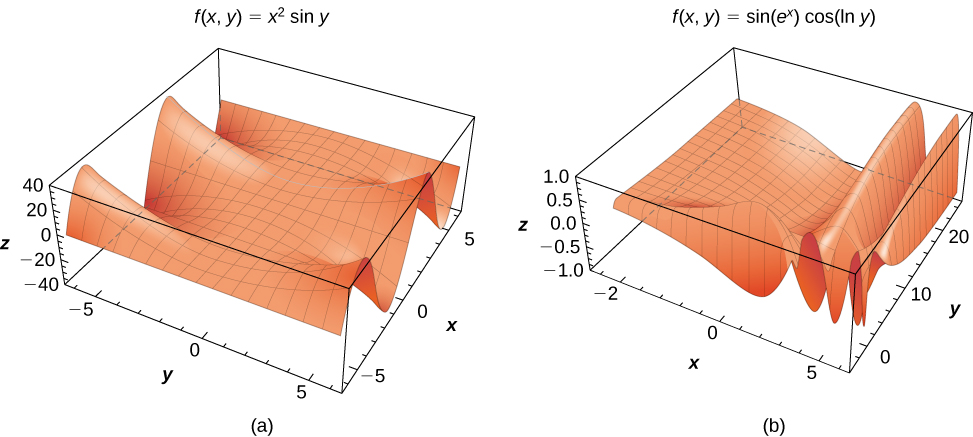
Les fonctions de deux variables peuvent produire des surfaces d'un aspect saisissant. La figure\(\PageIndex{11}\) montre deux exemples.

Figure\(\PageIndex{11}\) : Exemples de surfaces représentant les fonctions de deux variables : (a) une combinaison d'une fonction de puissance et d'une fonction sinusoïdale et (b) une combinaison de fonctions trigonométriques, exponentielles et logarithmiques.

Fonctions de plus de deux variables

Jusqu'à présent, nous n'avons examiné que les fonctions de deux variables. Cependant, il est utile d'examiner brièvement les fonctions de plus de deux variables. Deux de ces exemples sont

\[ \underbrace{f(x,y,z)=x^2−2xy+y^2+3yz−z^2+4x−2y+3x−6}_{\text{a polynomial in three variables}} \nonumber \]

et

\[g(x,y,t)=(x^2−4xy+y^2)\sin t−(3x+5y)\cos t. \nonumber \]

Dans la première fonction,\((x,y,z)\) représente un point dans l'espace, et la fonction\(f\) mappe chaque point de l'espace à une quatrième quantité, telle que la température ou la vitesse du vent. Dans la deuxième fonction,\((x,y)\) peut représenter un point dans le plan et\(t\) peut représenter le temps. La fonction peut mapper un point du plan avec une troisième quantité (par exemple, la pression) à un moment donné\(t\). La méthode pour trouver le domaine d'une fonction de plus de deux variables est analogue à la méthode pour les fonctions d'une ou deux variables.

Exemple\(\PageIndex{6}\): Domains for Functions of Three Variables

Trouvez le domaine de chacune des fonctions suivantes :

1. \(f(x,y,z)=\dfrac{3x−4y+2z}{\sqrt{9−x^2−y^2−z^2}}\)
2. \(g(x,y,t)=\dfrac{\sqrt{2t−4}}{x^2−y^2}\)

Solution :

a. Pour que la fonction\(f(x,y,z)=\dfrac{3x−4y+2z}{\sqrt{9−x^2−y^2−z^2}}\) soit définie (et qu'elle soit une valeur réelle), deux conditions doivent être remplies :

1. Le dénominateur ne peut pas être nul.
2. Le radical ne peut pas être négatif.

La combinaison de ces conditions conduit à l'inégalité

\[9−x^2−y^2−z^2>0.\nonumber \]

Déplacer les variables de l'autre côté et inverser l'inégalité donne au domaine

\[domain(f)=\{(x,y,z)∈R^3∣x^2+y^2+z^2<9\},\nonumber \]

qui décrit une boule de rayon\(3\) centrée à l'origine. (Remarque : la surface de la balle n'est pas incluse dans ce domaine.)

b. Pour que la fonction\(g(x,y,t)=\dfrac{\sqrt{2t−4}}{x^2−y^2}\) soit définie (et soit une valeur réelle), deux conditions doivent être remplies :

1. Le radical ne peut pas être négatif.
2. Le dénominateur ne peut pas être nul.

Puisque le radical ne peut pas être négatif, cela implique\(2t−4≥0\), et donc que\(t≥2\). Puisque le dénominateur ne peut pas être zéro\(x^2−y^2≠0\), ou\(x^2≠y^2\), Qui peut être réécrit comme\(y=±x\), quelles sont les équations de deux lignes passant par l'origine. Par conséquent, le domaine de\(g\) est

\[ domain(g)=\{(x,y,t)|y≠±x,t≥2\}. \nonumber \]

Exercice\(\PageIndex{4}\)

Trouvez le domaine de la fonction\(h(x,y,t)=(3t−6)\sqrt{y−4x^2+4}\).

Allusion

Vérifiez les valeurs qui rendent les radicaux négatifs ou les dénominateurs égaux à zéro.

Solution

\[domain(h)=\{(x,y,t)\in \mathbb{R}^3∣y≥4x^2−4\} \nonumber \]

Les fonctions de deux variables ont des courbes de niveau, qui sont affichées sous forme de courbes dans\(xy-plane.\) Cependant, lorsque la fonction comporte trois variables, les courbes deviennent des surfaces. Nous pouvons donc définir des surfaces de niveau pour les fonctions de trois variables.

Définition : surface plane d'une fonction à trois variables

Étant donné une fonction\(f(x,y,z)\) et un nombre compris\(c\) dans la plage de\(f\), une surface plane d'une fonction à trois variables est définie comme étant l'ensemble des points satisfaisant à l'équation\(f(x,y,z)=c.\)

Exemple\(\PageIndex{7}\): Finding a Level Surface

Trouvez la surface plane pour la fonction\(f(x,y,z)=4x^2+9y^2−z^2\) correspondant à\(c=1\).

Solution

La surface plane est définie par l'équation.\(4x^2+9y^2−z^2=1.\) Cette équation décrit un hyperboloïde d'une feuille, comme le montre la figure\(\PageIndex{12}\).

Figure\(\PageIndex{12}\) : Hyperboloïde représentant une feuille avec certaines de ses surfaces planes.

Exercice\(\PageIndex{5}\)

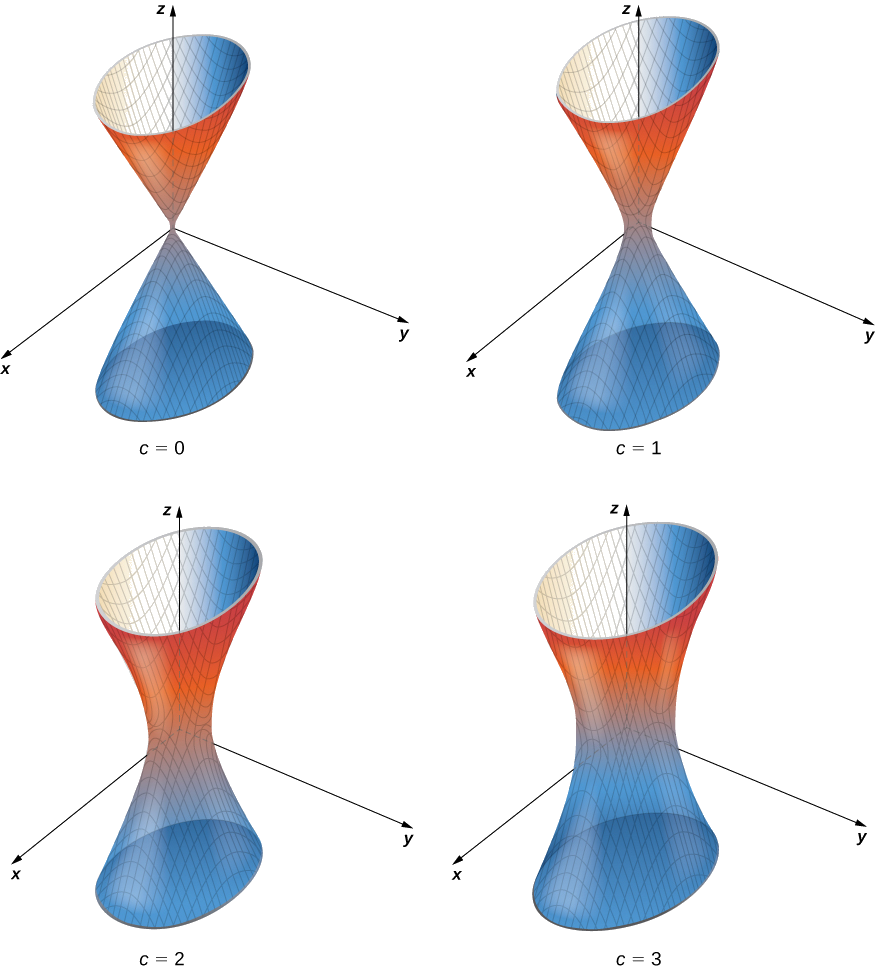
Trouvez l'équation de la surface plane de la fonction

\[ g(x,y,z)=x^2+y^2+z^2−2x+4y−6z \nonumber \]

correspondant à la surface\(c=2,\) et la décrivant, si possible.

Allusion

Définissez\(g(x,y,z)=c\) et complétez le carré.

Solution

((x−1) ^2+ (y+2) ^2+ (z−3) ^2=16 \) décrit une sphère de rayon\(4\) centrée sur le point\((1,−2,3).\)

Résumé

• Le graphe d'une fonction de deux variables est une surface\(\mathbb{R}^3\) et peut être étudié à l'aide de courbes de niveau et de tracés verticaux.
• Un ensemble de courbes de niveau est appelé carte de contour.

Équations clés

• Trace verticale

\(f(a,y)=z\)pour\(x=a\) ou\(f(x,b)=z\) pour\(y=b\)

• Surface plane d'une fonction à trois variables

\(f(x,y,z)=c\)

Lexique

carte des contours

un diagramme des différentes courbes de niveau d'une fonction donnée\(f(x,y)\)

fonction de deux variables

une fonction\(z=f(x,y)\) qui mappe chaque paire ordonnée\((x,y)\) d'un sous-ensemble\(D\) de\(R^2\) à un nombre réel unique\(z\)

graphe d'une fonction de deux variables

un ensemble de triples ordonnés\((x,y,z)\) qui satisfait l'équation\(z=f(x,y)\) tracée dans un espace cartésien tridimensionnel

courbe de niveau d'une fonction de deux variables

l'ensemble de points satisfaisant à l'équation\(f(x,y)=c\) d'un nombre réel compris\(c\) dans la plage de\(f\)

surface plane d'une fonction à trois variables

l'ensemble de points satisfaisant à l'équation\(f(x,y,z)=c\) d'un nombre réel compris\(c\) dans la plage de\(f\)

surface

le graphe d'une fonction de deux variables,\(z=f(x,y)\)

trace verticale

l'ensemble de triples ordonnés\((c,y,z)\) qui résout l'équation\(f(c,y)=z\) d'une constante donnée\(x=c\) ou l'ensemble de triples ordonnés\((x,d,z)\) qui résout l'équation\(f(x,d)=z\) d'une constante donnée\(y=d\)