3.4 : Les triangles, les rectangles et le théorème de Pythagore

Objectifs d'apprentissage

À la fin de cette section, vous serez en mesure de :

• Résoudre des applications en utilisant les propriétés des triangles
• Utilisez le théorème de Pythagore
• Résolvez des applications à l'aide

Soyez prêts

Avant de commencer, répondez à ce questionnaire de préparation.

1. Simplifiez :\(12(6h)\).
   Si vous avez oublié ce problème, passez en revue l'exercice 1.10.1.
2. La longueur d'un rectangle est inférieure de trois à sa largeur. Soit w la largeur. Écrivez une expression pour la longueur du rectangle.
   Si vous avez oublié ce problème, passez en revue l'exercice 1.3.43.
3. Résolvez :\(A=\frac{1}{2}bh\) pour b lorsque A=260 et h=52.
   Si vous avez oublié ce problème, passez en revue l'exercice 2.6.10.
4. Simplifiez :\(\sqrt{144}\).
   Si vous avez oublié ce problème, passez en revue l'exercice 1.9.10.

Résoudre des applications en utilisant les propriétés des triangles

Dans cette section, nous utiliserons certaines formules de géométrie courantes. Nous adapterons notre stratégie de résolution de problèmes afin de pouvoir résoudre les applications de géométrie. La formule géométrique nommera les variables et nous donnera l'équation à résoudre. De plus, étant donné que ces applications impliquent toutes des formes, la plupart des gens trouvent utile de dessiner une figure et de l'étiqueter avec les informations fournies. Nous l'inclurons dans la première étape de la stratégie de résolution de problèmes pour les applications de géométrie.

RÉSOUDRE DES APPLICATIONS GÉOMÉ

1. Lisez le problème et assurez-vous que tous les mots et toutes les idées sont compris. Dessinez la figure et étiquetez-la avec les informations données.
2. Identifiez ce que nous recherchons.
3. Étiquetez ce que vous recherchez en choisissant une variable pour le représenter.
4. Traduisez en équation en écrivant la formule ou le modèle approprié à la situation. Remplacer dans les informations données.
5. Résolvez l'équation en utilisant de bonnes techniques d'algèbre.
6. Vérifiez la réponse en la replaçant dans l'équation résolue à l'étape 5 et en vous assurant qu'elle est logique dans le contexte du problème.
7. Répondez à la question par une phrase complète.

Nous allons commencer les applications de géométrie en examinant les propriétés des triangles. Passons en revue quelques faits de base sur les triangles. Les triangles ont trois côtés et trois angles intérieurs. En général, chaque côté est étiqueté avec une lettre minuscule qui correspond à la lettre majuscule du sommet opposé.

Le pluriel du mot sommet est sommets. Tous les triangles ont trois sommets. Les triangles sont nommés par leurs sommets : le triangle de la figure\(\PageIndex{1}\) est appelé\(\triangle{ABC}\).

Figure\(\PageIndex{1}\) : Le triangle ABC possède des sommets\(A\)\(B\), et\(C\). Les longueurs des côtés sont\(a\)\(b\), et\(c\).

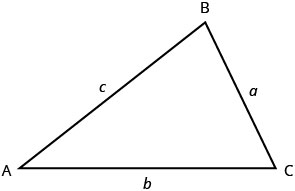
Les trois angles d'un triangle sont liés d'une manière particulière. La somme de leurs mesures est de\(180^{\circ}\). Notez que nous nous lisons\(m\angle{A}\) comme « la mesure de l'angle A. » Donc\(\triangle{ABC}\) dans la figure\(\PageIndex{1}\).

\[m \angle A+m \angle B+m \angle C=180^{\circ} \nonumber\]

Comme le périmètre d'une figure est la longueur de sa limite, le périmètre de\(\triangle{ABC}\) est la somme des longueurs de ses trois côtés.

\[P = a + b + c \nonumber\]

Pour trouver l'aire d'un triangle, nous devons connaître sa base et sa hauteur. La hauteur est une ligne qui relie la base au sommet opposé et forme un\(90^\circ\) angle avec la base. Nous allons dessiner\(\triangle{ABC}\) à nouveau, et maintenant afficher la hauteur,\(h\). Voir la figure\(\PageIndex{2}\).

Figure\(\PageIndex{2}\) : La formule pour l'aire de\(\triangle{ABC}\) est\(A = \frac{1}{2}bh\) où b est la base et h est la hauteur.

PROPRIÉTÉS DU TRIANGLE

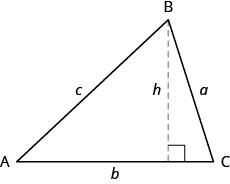
Pour\(\triangle{ABC}\)

Mesures d'angle :

\[m \angle A+m \angle B+m \angle C=180^{\circ}\]

• La somme des mesures des angles d'un triangle est de 180°.

Périmètre :

\[P = a + b + c\]

• Le périmètre est la somme des longueurs des côtés du triangle.

Région :

\(A = \frac{1}{2}bh, b = \text{ base }, h = \text{ height }\)

• L'aire d'un triangle est égale à la moitié de la base multipliée par la hauteur.

Exemple\(\PageIndex{1}\)

Les mesures des deux angles d'un triangle sont de 55 et 82 degrés. Détermine la mesure du troisième angle.

Solution

Étape 1. Lisez le problème. Dessinez la figure et étiquetez-la avec les informations données.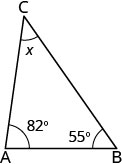
Étape 2. Identifiez ce que vous recherchez.	la mesure du troisième angle dans un triangle
Étape 3. Nom. Choisissez une variable pour la représenter.	Laissez\(x=\) la mesure de l'angle.
Étape 4. Traduisez.
Écrivez la formule appropriée et remplacez-la.	\(m \angle A+m \angle B+m \angle C=180^{\circ}\)
Étape 5. Résolvez l'équation.	\(\begin{array} {rll} {55 + 82 + x} &{=} &{180} \\ {137 + x} &{=} &{180} \\ {x} &{=} &{43} \end{array}\)
Étape 6. Vérifiez. \(\begin{array} {rll} {55 + 82 + 43} &{\stackrel{?}{=}} &{180} \\ {180} &{=} &{180\checkmark} \end{array}\)
Étape 7. Réponds à la question.	La mesure du troisième angle est de 43 degrés.

Essayez-le\(\PageIndex{1}\)

Les mesures des deux angles d'un triangle sont de 31 et 128 degrés. Détermine la mesure du troisième angle.

Réponse

21 degrés

Essayez-le\(\PageIndex{2}\)

Les mesures des deux angles d'un triangle sont de 49 et 75 degrés. Détermine la mesure du troisième angle.

Réponse

56 degrés

Exemple\(\PageIndex{2}\)

Le périmètre d'un jardin triangulaire est de 24 pieds. La longueur des deux côtés est de quatre pieds et neuf pieds. Quelle est la longueur du troisième côté ?

Solution

Étape 1. Lisez le problème. Dessinez la figure et étiquetez-la avec les informations données.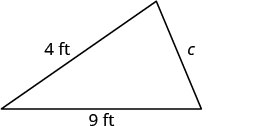
Étape 2. Identifiez ce que vous recherchez.	longueur du troisième côté d'un triangle
Étape 3. Nom. Choisissez une variable pour la représenter.	Laissez\(c=\) le troisième côté.
Étape 4. Traduisez.
Écrivez la formule appropriée et remplacez-la.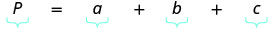
Remplacer dans les informations données.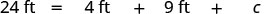
Étape 5. Résolvez l'équation.
Étape 6. Vérifiez. \(\begin{array} {rll} {P} &{=} &{a + b +c} \\ {24} &{\stackrel{?}{=}} &{4 + 9+11} \\ {24} &{=} &{24\checkmark} \end{array}\)
Étape 7. Réponds à la question.	Le troisième côté mesure 11 pieds de long.

Essayez-le\(\PageIndex{3}\)

Le périmètre d'un jardin triangulaire est de 48 pieds. Les longueurs des deux côtés sont de 18 pieds et 22 pieds. Quelle est la longueur du troisième côté ?

Réponse

8 pieds

Essayez-le\(\PageIndex{4}\)

La longueur des deux côtés d'une fenêtre triangulaire est de sept pieds et cinq pieds. Le périmètre est de 18 pieds. Quelle est la longueur du troisième côté ?

Réponse

6 pieds

Exemple\(\PageIndex{3}\)

La superficie d'une fenêtre d'église triangulaire est de 90 mètres carrés. La base de la fenêtre mesure 15 mètres. Quelle est la hauteur de la fenêtre ?

Solution

Étape 1. Lisez le problème. Dessinez la figure et étiquetez-la avec les informations données.	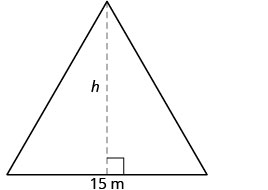\(\text{ Area } = 90m^{2}\)
Étape 2. Identifiez ce que vous recherchez.	hauteur d'un triangle
Étape 3. Nom. Choisissez une variable pour la représenter.	Laissez\(h=\) la hauteur.
Étape 4. Traduire.
Écrivez la formule appropriée.
Remplacer dans les informations données.
Étape 5. Résolvez l'équation.	\(90 = \dfrac{15}{2}h\) \(12 = h\)
Étape 6. Vérifiez. \(\begin{array} {rll} {A} &{=} &{\frac{1}{2}bh} \\ {90} &{\stackrel{?}{=}} &{\frac{1}{2}\cdot 15\cdot 12} \\ {90} &{=} &{90\checkmark} \end{array}\)
Étape 7. Réponds à la question.	La hauteur du triangle est de 12 mètres.

Essayez-le\(\PageIndex{5}\)

La superficie d'une peinture triangulaire est de 126 pouces carrés. La base mesure 18 pouces. Quelle est la hauteur ?

Réponse

14 pouces

Essayez-le\(\PageIndex{6}\)

Une porte de tente triangulaire a une superficie de 15 pieds carrés. La hauteur est de cinq pieds. Qu'est-ce que la base ?

Réponse

6 pieds

Les propriétés de triangle que nous avons utilisées jusqu'à présent s'appliquent à tous les triangles. Nous allons maintenant examiner un type spécifique de triangle : le triangle droit. Un triangle droit a un angle de 90°, que nous marquons généralement par un petit carré dans le coin.

Figurine\(\PageIndex{3}\)

Définition : TRIANGLE DROIT

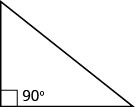
Un triangle droit possède un angle de 90°, qui est souvent marqué par un carré au sommet.

Exemple\(\PageIndex{4}\)

L'un des angles d'un triangle droit mesure 28°. Quelle est la mesure du troisième angle ?

Solution

Étape 1. Lisez le problème. Dessinez la figure et étiquetez-la avec les informations données.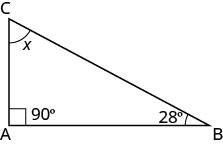
Étape 2. Identifiez ce que vous recherchez.	la mesure d'un angle
Étape 3. Nom. Choisissez une variable pour la représenter.	Laissez\(x=\) la mesure d'un angle.
Étape 4. Traduire.	\(m\angle{A} + m\angle{B} + m\angle{C} = 180\)
Écrivez la formule appropriée et remplacez-la.	\(x+90+28=180\)
Étape 5. Résolvez l'équation.	\(x=62\)
Étape 6. Vérifiez. \(\begin{array} {rll} {180} &{\stackrel{?}{=}} &{90+28+62} \\ {180} &{=} &{180\checkmark} \end{array}\)
Étape 7. Réponds à la question.	La mesure du troisième angle est de 62 ^°.

Essayez-le\(\PageIndex{7}\)

L'un des angles d'un triangle droit mesure 56°. Quelle est la mesure de l'autre petit angle ?

Réponse

34°

Essayez-le\(\PageIndex{8}\)

L'un des angles d'un triangle droit mesure 45°. Quelle est la mesure de l'autre petit angle ?

Réponse

45°

Dans les exemples que nous avons vus jusqu'à présent, nous pourrions dessiner une figure et l'étiqueter directement après avoir lu le problème. Dans l'exemple suivant, nous devrons définir un angle par rapport à un autre. Nous attendrons pour dessiner la figure jusqu'à ce que nous écrivions des expressions pour tous les angles que nous recherchons.

Exemple\(\PageIndex{5}\)

La mesure d'un angle d'un triangle droit est supérieure de 20 degrés à la mesure du plus petit angle. Trouvez les mesures des trois angles.

Solution

Étape 1. Lisez le problème.
Étape 2. Identifiez ce que vous recherchez.	les mesures des trois angles
Étape 3. Nom. Choisissez une variable pour la représenter.	Laissez\(a=1^{st}\) l'angle. \(a+20=2^{nd}\) \(90=3^{rd}\)angle d'angle (angle droit)
Dessinez la figure et étiquetez-la avec les informations données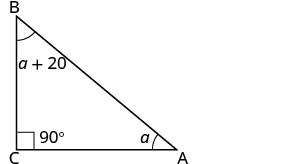
Étape 4. TRADUIRE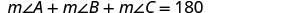
Écrivez la formule appropriée. Substituer dans la formule.	\(a + (a + 20) + 90 = 180\)
Étape 5. Résolvez l'équation.	\ (\ begin {align*} 2a + 110 &= 180 \ \ [3 points] 2a &= 70 \ \ [3 points] a &= 35 \ text {premier angle} \ \ [3 points] a &+ 20 \ text {deuxième angle} \ \ [3 points] {\ color {rouge} {35}} &+ 20 = 55 \ end {align*} \) Et le troisième angle est de 90.
Étape 6. Vérifiez. \(\begin{array} {rll} {35 + 55 + 90} &{\stackrel{?}{=}} &{180} \\ {180} &{=} &{180\checkmark} \end{array}\)
Étape 7. Réponds à la question.	Les trois angles mesurent 35 ^°, 55 ^° et 90 ^°.

Essayez-le\(\PageIndex{9}\)

La mesure d'un angle d'un triangle droit est supérieure de 50 degrés à la mesure du plus petit angle. Trouvez les mesures des trois angles.

Réponse

20°, 70°, 90°

Essayez-le\(\PageIndex{10}\)

La mesure d'un angle d'un triangle droit est supérieure de 30° à la mesure du plus petit angle. Trouvez les mesures des trois angles.

Réponse

30°, 60°, 90°

Utilisez le théorème de Pythagore

Nous avons appris comment les mesures des angles d'un triangle sont liées les unes aux autres. Nous allons maintenant apprendre comment les longueurs des côtés sont liées les unes aux autres. Le théorème de Pythagore est une propriété importante qui décrit la relation entre les longueurs des trois côtés d'un triangle droit. Ce théorème est utilisé dans le monde entier depuis l'Antiquité. Il doit son nom au philosophe et mathématicien grec Pythagore, qui a vécu environ 500 ans avant JC.

Avant d'énoncer le théorème de Pythagore, nous devons introduire quelques termes pour désigner les côtés d'un triangle. N'oubliez pas qu'un triangle droit a un angle de 90°, marqué par un petit carré dans le coin. Le côté du triangle opposé à l'angle de 90°90° est appelé hypoténuse et chacun des autres côtés est appelé jambes.

Figurine\(\PageIndex{4}\)

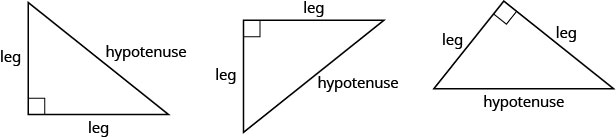
Le théorème de Pythagore indique comment les longueurs des trois côtés d'un triangle droit sont liées les unes aux autres. Il indique que dans tout triangle droit, la somme des carrés des longueurs des deux jambes est égale au carré de la longueur de l'hypoténuse. En symboles, nous disons : dans n'importe quel triangle droit\(a^{2}+b^{2}=c^{2}\), où a et b sont la longueur des jambes et cc est la longueur de l'hypoténuse.

Écrire la formule dans chaque exercice et la dire à haute voix pendant que vous l'écrivez peut vous aider à vous souvenir du théorème de Pythagore.

LE THÉORÈME DE PYTHAGORE

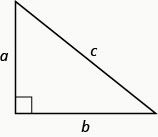
Dans tout triangle droit, où\(a\) et se\(b\) trouvent les longueurs des jambes,\(c\) se trouve la longueur de l'hypoténuse.

Alors

\[a^{2}+b^{2}=c^{2} \label{Ptheorem}\]

Pour résoudre des exercices utilisant le théorème de Pythagore (équation \ ref {Pthéorème}), nous devrons trouver des racines carrées. Nous avons utilisé la notation\(\sqrt{m}\) et la définition :

Si\(m = n^{2}\), alors\(\sqrt{m} = n\), pour\(n\geq 0\).

Par exemple, nous avons constaté que\(\sqrt{25}\) c'est 5 parce que\(25=5^{2}\).

Comme le théorème de Pythagore contient des variables au carré, pour déterminer la longueur d'un côté dans un triangle droit, nous devrons utiliser des racines carrées.

Exemple\(\PageIndex{6}\)

Utilisez le théorème de Pythagore pour déterminer la longueur de l'hypoténuse indiquée ci-dessous.

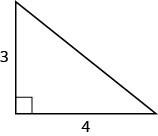
Solution

Étape 1. Lisez le problème.
Étape 2. Identifiez ce que vous recherchez.	la longueur de l'hypoténuse du triangle
Étape 3. Nom. Choisissez une variable pour la représenter. Étiquette sur la face C de la figure.	Soit c = la longueur de l'hypoténuse.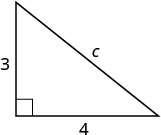
Étape 4. Traduire.
Écrivez la formule appropriée.	\(a^{2} + b^{2} = c^{2}\)
Substitut.	\(3^{2}+4^{2}=c^{2}\)
Étape 5. Résolvez l'équation.	\(9+16=c^{2}\)
Simplifiez.	\(25=c^{2}\)
Utilisez la définition de la racine carrée.	\(\sqrt{25} = c\)
Simplifiez.	\(5=c\)
Étape 6. Vérifiez.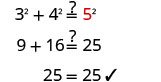
Étape 7. Réponds à la question.	La longueur de l'hypoténuse est de 5.

Essayez-le\(\PageIndex{11}\)

Utilisez le théorème de Pythagore pour déterminer la longueur de l'hypoténuse dans le triangle ci-dessous.

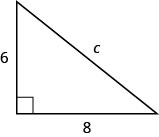
Réponse

c=10

Essayez-le\(\PageIndex{12}\)

Utilisez le théorème de Pythagore pour déterminer la longueur de l'hypoténuse dans le triangle ci-dessous.

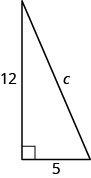
Réponse

c=13

Exemple\(\PageIndex{7}\)

Utilisez le théorème de Pythagore pour trouver la longueur de la jambe indiquée ci-dessous.

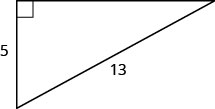
Solution

Étape 1. Lisez le problème.
Étape 2. Identifiez ce que vous recherchez.	la longueur de la jambe du triangle
Étape 3. Nom. Choisissez une variable pour la représenter.	Laissez\(b=\) la jambe du triangle.
Côté étiquette\(b\).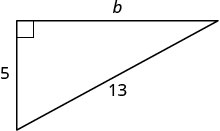
Étape 4. TRADUIRE
Écrivez la formule appropriée.	\(a^{2} + b^{2} = c^{2}\)
Substitut.	\(5^{2}+b^{2}=13^{2}\)
Étape 5. Résolvez l'équation.	\(25+b^{2}=169\)
Isolez le terme variable.	\(b^{2}=144\)
Utilisez la définition de la racine carrée.	\(b = \sqrt{144}\)
Simplifiez.	\(b=12\)
Étape 6. Vérifiez.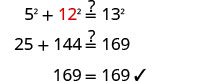
Étape 7. Réponds à la question.	La longueur de la jambe est de 12.

Essayez-le\(\PageIndex{13}\)

Utilisez le théorème de Pythagore pour déterminer la longueur de la jambe dans le triangle ci-dessous.

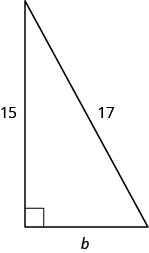
Réponse

8

Essayez-le\(\PageIndex{14}\)

Utilisez le théorème de Pythagore pour déterminer la longueur de la jambe dans le triangle ci-dessous.

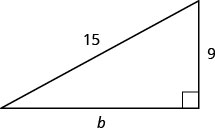
Réponse

12

Exemple\(\PageIndex{8}\)

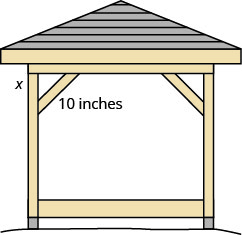
Kelvin construit un belvédère et veut renforcer chaque coin en plaçant un morceau de bois de 10 pouces en diagonale, comme indiqué ci-dessus.

S'il attache le bois de manière à ce que les extrémités de l'entretoise soient à la même distance du coin, quelle est la longueur des pieds du triangle droit formé ? Environ au dixième de pouce le plus proche.

Solution

\(\begin{array} {ll} {\textbf{Step 1. }\text{Read the problem.}} &{} \\\\ {\textbf{Step 2. }\text{Identify what we are looking for.}} &{\text{the distance from the corner that the}} \\ {} &{\text{bracket should be attached}} \\ \\{\textbf{Step 3. }\text{Name. Choose a variable to represent it.}} &{\text{Let x = distance from the corner.}} \\ {\textbf{Step 4.} \text{Translate}} &{} \\ {\text{Write the appropriate formula and substitute.}} &{a^{2} + b^{2} = c^{2}} \\ {} &{x^{2} + x^{2} = 10^{2}} \\ \\ {\textbf{Step 5. Solve the equation.}} &{} \\ {} &{2x^{2} = 100} \\ {\text{Isolate the variable.}} &{x^{2} = 50} \\ {\text{Simplify. Approximate to the nearest tenth.}} &{x \approx 7.1}\\\\ {\textbf{Step 6. }\text{Check.}} &{}\\ {a^{2} + b^{2} = c^{2}} &{} \\ {(7.1)^{2} + (7.1)^{2} \approx 10^{2} \text{ Yes.}} &{} \\\\ {\textbf{Step 7. Answer the question.}} &{\text{Kelven should fasten each piece of}} \\ {} &{\text{wood approximately 7.1'' from the corner.}} \end{array}\)

Essayez-le\(\PageIndex{15}\)

John place la base d'une échelle de 13 pieds à cinq pieds du mur de sa maison, comme indiqué ci-dessous. À quelle hauteur du mur s'élève l'échelle ?

Réponse

12 pieds

Essayez-le\(\PageIndex{16}\)

Randy souhaite fixer une guirlande lumineuse de 17 pieds au sommet du mât de 15 pieds de son voilier, comme indiqué ci-dessous. À quelle distance de la base du mât doit-il fixer l'extrémité de la guirlande lumineuse ?

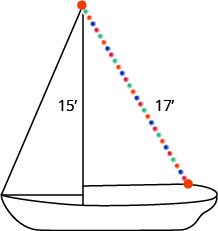
Réponse

8 pieds

Résoudre des applications en utilisant les propriétés

Vous connaissez peut-être déjà les propriétés des rectangles. Les rectangles ont quatre côtés et quatre angles droits (90°). Les côtés opposés d'un rectangle ont la même longueur. Nous désignons un côté du rectangle par la longueur\(L\), et son côté adjacent par la largeur,\(W\).

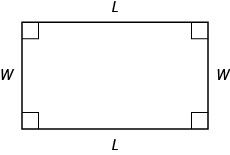
La distance autour de ce rectangle est\(L+W+L+W\), ou\(2L+2W\). C'est le \(P\)périmètre du rectangle.

\[P=2L+2W\]

Qu'en est-il de l'aire d'un rectangle ? Imaginez un tapis rectangulaire de 2 pieds de long sur 3 pieds de large. Sa superficie est de 6 pieds carrés. Il y a six carrés sur la figure.

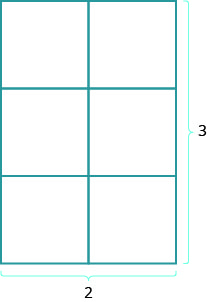
\[\begin{array} {l} {A=6} \\ {A=2\cdot3} \\ {A=L\cdot W} \end{array}\]

La surface est la longueur multipliée par la largeur. La formule pour l'aire d'un rectangle est

\[A=LW.\]

PROPRIÉTÉS DES RECTANGLES

Les rectangles ont quatre côtés et quatre angles droits (90°).

Les longueurs des côtés opposés sont égales.

Le périmètre d'un rectangle est la somme du double de la longueur et du double de la largeur.

\[P=2L+2W\]

L'aire d'un rectangle est le produit de la longueur et de la largeur.

\[A=L·W\]

Exemple\(\PageIndex{9}\)

La longueur d'un rectangle est de 32 mètres et la largeur de 20 mètres. Quel est le périmètre ?

Solution

Étape 1. Lisez le problème. Dessinez la figure et étiquetez-la avec les informations données.
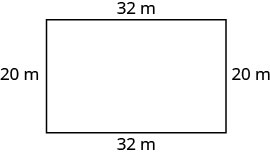Étape 2. Identifiez ce que vous recherchez.	le périmètre d'un rectangle
Étape 3. Nom. Choisissez une variable pour la représenter.	Laissez\(P=\) le périmètre.
Étape 4. Traduisez.
Écrivez la formule appropriée.
Substitut.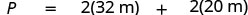
Étape 5. Résolvez l'équation.	\(P = 64 + 40\) \(P = 104\)
Étape 6. Vérifiez. \(\begin{array} {rcl} {P} &{\stackrel{?}{=}} &{104} \\ {20+32+20+32} &{\stackrel{?}{=}} &{104} \\ {104} &{=} &{104\checkmark} \end{array}\)
Étape 7. Réponds à la question.	Le périmètre du rectangle est de 104 mètres.

Essayez-le\(\PageIndex{17}\)

La longueur d'un rectangle est de 120 mètres et la largeur de 50 mètres. Quel est le périmètre ?

Réponse

340 mètres

Essayez-le\(\PageIndex{18}\)

La longueur d'un rectangle est de 62 pieds et la largeur de 48 pieds. Quel est le périmètre ?

Réponse

220 pieds

Exemple\(\PageIndex{10}\)

La superficie d'une pièce rectangulaire est de 168 pieds carrés. La longueur est de 14 pieds. Quelle est la largeur ?

Solution

Étape 1. Lisez le problème. Dessinez la figure et étiquetez-la avec les informations données.
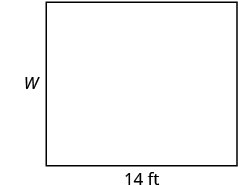Étape 2. Identifiez ce que vous recherchez.	la largeur d'une pièce rectangulaire
Étape 3. Nom. Choisissez une variable pour la représenter.	Laissez\(W=\) la largeur.
Étape 4. Traduisez.
Écrivez la formule appropriée.	\(A=LW\)
Substitut.	\(168 = 14W\)
Étape 5. Résolvez l'équation.	\(\frac{168}{14} = \frac{14W}{14}\) \(12 = W\)
Étape 6. Vérifiez. \(\begin{array} {rcl} {A} &{=} &{LW} \\ {168} &{\stackrel{?}{=}} &{14\cdot 12} \\ {168} &{=} &{168\checkmark} \end{array}\)
Étape 7. Réponds à la question.	La largeur de la pièce est de 12 pieds.

Essayez-le\(\PageIndex{19}\)

La superficie d'un rectangle est de 598 pieds carrés. La longueur est de 23 pieds. Quelle est la largeur ?

Réponse

26 pieds

Essayez-le\(\PageIndex{20}\)

La largeur d'un rectangle est de 21 mètres. La superficie est de 609 mètres carrés. Quelle est la longueur ?

Réponse

29 mètres

Exemple\(\PageIndex{11}\)

Détermine la longueur d'un rectangle avec un périmètre de 50 pouces et une largeur de 10 pouces.

Solution

Étape 1. Lisez le problème. Dessinez la figure et étiquetez-la avec les informations données.
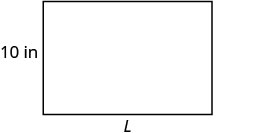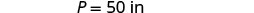Étape 2. Identifiez ce que vous recherchez.	la longueur du rectangle
Étape 3. Nom. Choisissez une variable pour la représenter.	Laissez\(L=\) la longueur.
Étape 4. Traduisez.
Écrivez la formule appropriée.	\(P = 2L + 2W\)
Substitut.	\(50 = 2L + 2(10)\)
Étape 5. Résolvez l'équation.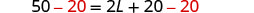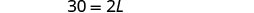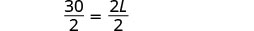
Étape 6. Vérifiez. \(\begin{array} {rcl} {P} &{=} &{50} \\ {15+10+15+10} &{\stackrel{?}{=}} &{50} \\ {50} &{=} &{50\checkmark} \end{array}\)
Étape 7. Réponds à la question.	La longueur est de 15 pouces.

Essayez-le\(\PageIndex{21}\)

Détermine la longueur d'un rectangle avec : périmètre 80 et largeur 25.

Réponse

15

Essayez-le\(\PageIndex{22}\)

Détermine la longueur d'un rectangle avec : périmètre 30 et largeur 6.

Réponse

9

Nous avons résolu des problèmes où la longueur ou la largeur étaient données, ainsi que le périmètre ou la surface ; nous allons maintenant apprendre comment résoudre les problèmes dans lesquels la largeur est définie en termes de longueur. Nous attendrons pour dessiner la figure jusqu'à ce que nous écrivions une expression pour la largeur afin de pouvoir étiqueter un côté avec cette expression.

Exemple\(\PageIndex{12}\)

La largeur d'un rectangle est inférieure de deux pieds à sa longueur. Le périmètre est de 52 pieds. Trouvez la longueur et la largeur.

Solution

Étape 1 Lisez le problème.
Étape 2 Identifiez ce que vous recherchez.	la longueur et la largeur d'un rectangle
Étape 3 Nom. Choisissez une variable pour la représenter. Puisque la largeur est définie en termes de longueur, nous laissons la\(L=\) longueur. La largeur est inférieure de deux pieds à la longueur, donc nous laissons la\(L-2\) largeur.	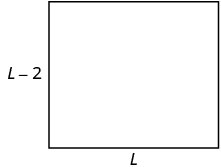\(P=52\)pieds
Étape 4. Traduisez.
Écrivez la formule appropriée. La formule du périmètre d'un rectangle met en relation toutes les informations.	\(P=2L+2W\)
Remplacer dans les informations données.	\(52=2L+2(L−2)\)
Étape 5. Résolvez l'équation.	\(52=2L+2L−4\)
Combinez les mêmes termes.	\(52=4L−4\)
Ajoutez-en 4 de chaque côté.	\(56 = 4L\)
Divisez par 4.	\(\frac{56}{4} = \frac{4L}{4}\) \(14=L\) La longueur est de 14 pieds.
Maintenant, nous devons trouver la largeur.	La largeur est de\(L−2\). La largeur est de 12 pieds.
Étape 6. Vérifiez. Depuis\(14+12+14+12=52\), cela fonctionne !
Étape 7. Réponds à la question.	La longueur est de 14 pieds et la largeur de 12 pieds.

Essayez-le\(\PageIndex{23}\)

La largeur d'un rectangle est inférieure de sept mètres à sa longueur. Le périmètre est de 58 mètres. Trouvez la longueur et la largeur.

Réponse

18 mètres, 11 mètres

Essayez-le\(\PageIndex{24}\)

La longueur d'un rectangle est supérieure de huit pieds à sa largeur. Le périmètre est de 60 pieds. Trouvez la longueur et la largeur.

Réponse

19 pieds, 11 pieds

Exemple\(\PageIndex{13}\)

La longueur d'un rectangle est de quatre centimètres, soit plus du double de la largeur. Le périmètre est de 32 centimètres. Trouvez la longueur et la largeur.

Solution

Étape 1 Lisez le problème.
Étape 2 Identifiez ce que vous recherchez.	la longueur et la largeur
Étape 3 Nom. Choisissez une variable pour représenter la largeur.
La longueur est quatre fois plus que deux fois la largeur.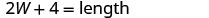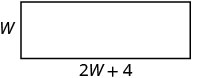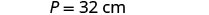
Étape 4. TRADUIRE
Écrivez la formule appropriée.	\(\quad P=2L+2W\)
Remplacer dans les informations données.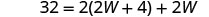
Étape 5. Résolvez l'équation.	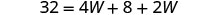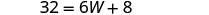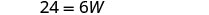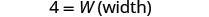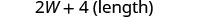12 La longueur est 12 cm
Étape 6. Vérifiez. 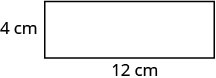\(\begin{array} {rcl} {P} &{=} &{2L + 2W} \\ {32} &{\stackrel{?}{=}} &{2\cdot 12 + 2\cdot 4} \\ {32} &{=} &{32\checkmark} \end{array}\)
Étape 7. Réponds à la question.	La longueur est de 12 cm et la largeur de 4 cm.

Essayez-le\(\PageIndex{25}\)

La longueur d'un rectangle est huit, soit plus du double de la largeur. Le périmètre est de 64. Trouvez la longueur et la largeur.

Réponse

24, 8

Essayez-le\(\PageIndex{26}\)

La largeur d'un rectangle est inférieure de six fois à sa longueur. Le périmètre est de 18. Trouvez la longueur et la largeur.

Réponse

5, 4

Exemple\(\PageIndex{14}\)

Le périmètre d'une piscine rectangulaire est de 150 pieds. La longueur est supérieure de 15 pieds à la largeur. Trouvez la longueur et la largeur.

Solution

Étape 1 Lisez le problème. Dessinez la figure et étiquetez-la avec les informations données.	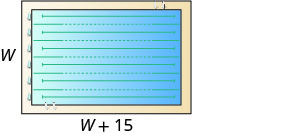\(P=150\)pieds
Étape 2 Identifiez ce que vous recherchez.	la longueur et la largeur de la piscine
Étape 3 Nom. Choisissez une variable pour représenter la largeur. La longueur est supérieure de 15 pieds à la largeur.
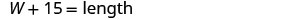Étape 4. TRADUIRE
Écrivez la formule appropriée.	\(\quad P=2L+2W\)
Substitut.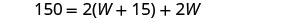
Étape 5. Résolvez l'équation.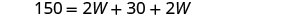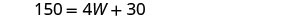
Étape 6. Vérifiez. \(\begin{array} {rcl} {P} &{=} &{2L + 2W} \\ {150} &{\stackrel{?}{=}} &{2(45) + 2(30)} \\ {150} &{=} &{150\checkmark} \end{array}\)
Étape 7. Réponds à la question.	La longueur de la piscine est de 45 pieds et la largeur de 30 pieds.

Essayez-le\(\PageIndex{27}\)

Le périmètre d'une piscine rectangulaire est de 200 pieds. La longueur est supérieure de 40 pieds à la largeur. Trouvez la longueur et la largeur.

Réponse

70 pieds, 30 pieds

Essayez-le\(\PageIndex{28}\)

La longueur d'un jardin rectangulaire est supérieure de 30 mètres à sa largeur. Le périmètre est de 300 mètres. Trouvez la longueur et la largeur.

Réponse

90 mètres, 60 mètres

Concepts clés

• Stratégie de résolution de problèmes pour les applications de géométrie
  1. Lisez le problème et faites comprendre tous les mots et toutes les idées. Dessinez la figure et étiquetez-la avec les informations données.
  2. Identifiez ce que nous recherchons.
  3. Nommez ce que vous recherchez en choisissant une variable pour le représenter.
  4. Traduisez en équation en écrivant la formule ou le modèle approprié à la situation. Remplacer dans les informations données.
  5. Résolvez l'équation en utilisant de bonnes techniques d'algèbre.
  6. Vérifiez la réponse au problème et assurez-vous qu'elle est logique.
  7. Répondez à la question par une phrase complète.
• Propriétés du triangle pour les mesures d'
  angle △ ABC :
  • \(m\angle{A}+m\angle{B}+m\angle{C}=180\)
  Périmètre :
  • \(P=a+b+c\)
  Région :
  • \(A=\frac{1}{2}bh\), b = base, h = hauteur
  Un triangle droit possède un angle de 90°.
• Le théorème de Pythagore Dans n'importe quel triangle droit,\(a^{2} + b^{2} = c^{2}\) où\(c\) est la longueur de l'hypoténuse\(a\) et où\(b\) sont les longueurs des jambes.
• Propriétés des rectangles
  • Les rectangles ont quatre côtés et quatre angles droits (90°).
  • Les longueurs des côtés opposés sont égales.
  • Le périmètre d'un rectangle est la somme de deux fois la longueur et du double de la largeur :\(P=2L+2W\).
  • La surface d'un rectangle est la longueur multipliée par la largeur :\(A=LW\).