14.8 : Multiplicateurs Lagrange
- Page ID
- 197395
- Utilisez la méthode des multiplicateurs de Lagrange pour résoudre les problèmes d'optimisation avec une seule contrainte.
- Utilisez la méthode des multiplicateurs de Lagrange pour résoudre les problèmes d'optimisation avec deux contraintes.
La résolution de problèmes d'optimisation pour les fonctions de deux variables ou plus peut être similaire à la résolution de tels problèmes dans le calcul à une seule variable. Cependant, les techniques permettant de traiter de multiples variables nous permettent de résoudre des problèmes d'optimisation plus variés pour lesquels nous devons faire face à des conditions ou des contraintes supplémentaires. Dans cette section, nous examinons l'une des méthodes les plus courantes et les plus utiles pour résoudre les problèmes d'optimisation avec des contraintes.
Multiplicateurs Lagrange
Dans la section précédente, une situation appliquée a été explorée impliquant la maximisation d'une fonction de profit, sous réserve de certaines contraintes. Dans cet exemple, les contraintes concernaient un nombre maximum de balles de golf pouvant être produites et vendues par\(1\) mois\((x),\) et un nombre maximum d'heures de publicité pouvant être achetées par mois\((y)\). Supposons qu'elles soient combinées en une seule contrainte budgétaire, par exemple\(20x+4y≤216\), qui tienne compte à la fois du coût de production des balles de golf et du nombre d'heures de publicité achetées par mois. L'objectif est toujours de maximiser les profits, mais il existe désormais un autre type de contrainte sur les valeurs de\(x\) et\(y\). Cette contrainte et la fonction de profit correspondante
\[f(x,y)=48x+96y−x^2−2xy−9y^2 \nonumber \]
est un exemple de problème d'optimisation, et la fonction\(f(x,y)\) est appelée fonction objective. Un graphique des différentes courbes de niveau de la fonction\(f(x,y)\) suit.
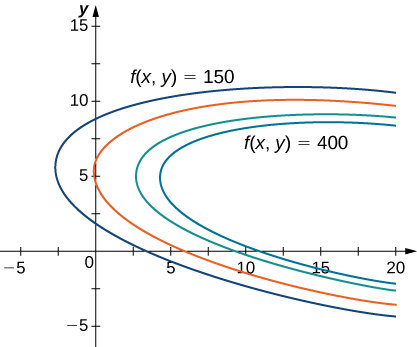
Dans la figure\(\PageIndex{1}\), la valeur\(c\) représente différents niveaux de profit (c'est-à-dire les valeurs de la fonction\(f\)). Lorsque la valeur de\(c\) augmente, la courbe se déplace vers la droite. Comme notre objectif est de maximiser les profits, nous voulons choisir une courbe la plus à droite possible. S'il n'y avait aucune restriction quant au nombre de balles de golf que l'entreprise pourrait produire ou au nombre d'unités de publicité disponibles, nous pourrions produire autant de balles de golf que nous le voulons et faire de la publicité autant que nous le voulons, sans que l'entreprise n'obtienne un maximum de bénéfices. Malheureusement, nous avons une contrainte budgétaire modélisée par l'inégalité.\(20x+4y≤216.\) Pour voir comment cette contrainte interagit avec la fonction de profit, la figure\(\PageIndex{2}\) montre le graphique de la ligne\(20x+4y=216\) superposée au graphique précédent.
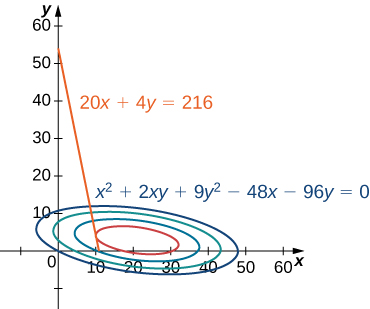
Comme indiqué précédemment, le profit maximal se produit lorsque la courbe de niveau est aussi éloignée que possible vers la droite. Toutefois, le niveau de production correspondant à ce bénéfice maximal doit également satisfaire à la contrainte budgétaire, de sorte que le point auquel ce bénéfice est réalisé doit également se situer sur (ou à gauche) de la ligne rouge de la figure\(\PageIndex{2}\). L'examen de ce graphique révèle que ce point existe où la droite est tangente à la courbe de niveau de\(f\). \(y\)Des essais et des erreurs révèlent que ce niveau de profit semble être\(395\) proche, alors\(x\) qu'il est légèrement inférieur à\(5\). Nous reviendrons sur la solution de ce problème plus loin dans cette section. D'un point de vue théorique, au point où la courbe de profit est tangente à la ligne de contrainte, le gradient des deux fonctions évaluées à ce point doit pointer dans la même direction (ou dans la direction opposée). Rappelons que le gradient d'une fonction de plusieurs variables est un vecteur. Si deux vecteurs pointent dans la même direction (ou dans des directions opposées), l'un doit être un multiple constant de l'autre. Cette idée est à la base de la méthode des multiplicateurs de Lagrange.
Théorème\(\PageIndex{1}\) : Fonctions de deux variables avec des dérivées partielles continues à chaque point d'un ensemble ouvert contenant la courbe lisse\(g(x,y)=0.\) Supposons que\(f\), lorsqu'il est limité à des points de la courbe\(g(x,y)=0\), ait un extremum local au point\(f\)\(g\)\((x_0,y_0)\) et ça\(\vecs ∇g(x_0,y_0)≠0\). Ensuite, il existe un nombre\(λ\) appelé multiplicateur de Lagrange, pour lequel
\[\vecs ∇f(x_0,y_0)=λ\vecs ∇g(x_0,y_0). \nonumber \]
Supposons qu'un extremum contraint se produise au point.\((x_0,y_0).\) De plus, nous supposons que l'équation\(g(x,y)=0\) peut être facilement paramétrée comme suit :
\(x=x(s) \; \text{and}\; y=y(s)\)
où\(s\) est un paramètre de longueur d'arc avec le point de référence\((x_0,y_0)\) à\(s=0\). Par conséquent, la quantité\(z=f(x(s),y(s))\) a un maximum relatif ou un minimum relatif à\(s=0\), ce qui implique qu'\(\dfrac{dz}{ds}=0\)à ce moment-là. À partir de la règle des chaînes,
\[\begin{align*} \dfrac{dz}{ds} &=\dfrac{∂f}{∂x}⋅\dfrac{∂x}{∂s}+\dfrac{∂f}{∂y}⋅\dfrac{∂y}{∂s} \\[4pt] &=\left(\dfrac{∂f}{∂x}\hat{\mathbf i}+\dfrac{∂f}{∂y}\hat{\mathbf j}\right)⋅\left(\dfrac{∂x}{∂s}\hat{\mathbf i}+\dfrac{∂y}{∂s}\hat{\mathbf j}\right)\\[4pt] &=0, \end{align*}\]
où les dérivés sont tous évalués à\(s=0\). Toutefois, le premier facteur du produit scalaire est le gradient de\(f\) et le second est le vecteur tangent unitaire\(\vec{\mathbf T}(0)\) à la courbe de contrainte. Comme le point\((x_0,y_0)\) correspond à\(s=0\), il ressort de cette équation que
\[\vecs ∇f(x_0,y_0)⋅\vecs{\mathbf T}(0)=0, \nonumber \]
ce qui implique que le gradient est soit le vecteur zéro,\(\vecs 0\) soit normal à la courbe de contrainte à un extremum relatif contraint. Cependant, la courbe de contrainte\(g(x,y)=0\) est une courbe de niveau pour la fonction\(\vecs ∇g(x_0,y_0)≠0\), de\(g(x,y)\) sorte que si elle\(\vecs ∇g(x_0,y_0)\) est normale à cette courbe à\((x_0,y_0)\) Il s'ensuit qu'il existe un scalaire\(λ\) tel que
\[\vecs ∇f(x_0,y_0)=λ\vecs ∇g(x_0,y_0) \nonumber \]
\(\square\)
Pour appliquer Theorem\(\PageIndex{1}\) à un problème d'optimisation similaire à celui du fabricant de balles de golf, nous avons besoin d'une stratégie de résolution de problèmes.
- Déterminer la fonction objectif\(f(x,y)\) et la fonction de contrainte Le problème d'optimisation\(g(x,y).\) implique-t-il de maximiser ou de minimiser la fonction objectif ?
- Configurez un système d'équations à l'aide du modèle suivant :\[\begin{align} \vecs ∇f(x_0,y_0) &=λ\vecs ∇g(x_0,y_0) \\[4pt] g(x_0,y_0) &=0 \end{align}. \nonumber \]
- Résolvez pour\(x_0\) et\(y_0\).
- La plus grande des valeurs des solutions trouvées\(f\) à l'étape\(3\) maximise\(f\) ; la plus petite de ces valeurs est minimisée\(f\).
Utilisez la méthode des multiplicateurs de Lagrange pour trouver la valeur minimale du\(f(x,y)=x^2+4y^2−2x+8y\) sujet soumis à la contrainte\(x+2y=7.\)
Solution
Suivons la stratégie de résolution des problèmes :
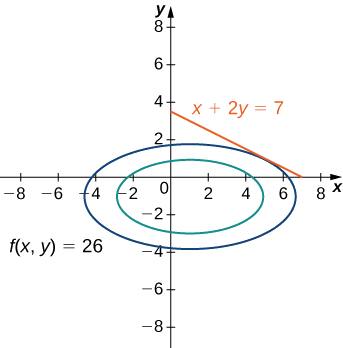
1. La fonction objective est\(f(x,y)=x^2+4y^2−2x+8y.\) Pour déterminer la fonction de contrainte, nous devons d'abord la\(7\) soustraire des deux côtés de la contrainte. Cela donne\(x+2y−7=0.\) que la fonction de contrainte est égale au côté gauche, donc\(g(x,y)=x+2y−7\). Le problème nous demande de le résoudre pour la valeur minimale de\(f\), sous réserve de la contrainte (Figure\(\PageIndex{3}\)).
2. Il faut ensuite calculer les gradients des deux\(f\) et\(g\) :
\[\begin{align*} \vecs \nabla f \left( x, y \right) &= \left( 2x - 2 \right) \hat{\mathbf{i}} + \left( 8y + 8 \right) \hat{\mathbf{j}} \\ \vecs \nabla g \left( x, y \right) &= \hat{\mathbf{i}} + 2 \hat{\mathbf{j}}. \end{align*}\]
L'équation\(\vecs \nabla f \left( x_0, y_0 \right) = \lambda \vecs \nabla g \left( x_0, y_0 \right)\) devient
\[\left( 2 x_0 - 2 \right) \hat{\mathbf{i}} + \left( 8 y_0 + 8 \right) \hat{\mathbf{j}} = \lambda \left( \hat{\mathbf{i}} + 2 \hat{\mathbf{j}} \right), \nonumber \]
qui peut être réécrit comme
\[\left( 2 x_0 - 2 \right) \hat{\mathbf{i}} + \left( 8 y_0 + 8 \right) \hat{\mathbf{j}} = \lambda \hat{\mathbf{i}} + 2 \lambda \hat{\mathbf{j}}. \nonumber \]
Ensuite, nous définissons les coefficients\(\hat{\mathbf{j}}\) égaux\(\hat{\mathbf{i}}\) et égaux les uns aux autres :
\[\begin{align*} 2 x_0 - 2 &= \lambda \\ 8 y_0 + 8 &= 2 \lambda. \end{align*}\]
L'équation\(g \left( x_0, y_0 \right) = 0\) devient\(x_0 + 2 y_0 - 7 = 0\). Par conséquent, le système d'équations à résoudre est
\[\begin{align*} 2 x_0 - 2 &= \lambda \\ 8 y_0 + 8 &= 2 \lambda \\ x_0 + 2 y_0 - 7 &= 0. \end{align*}\]
3. Il s'agit d'un système linéaire de trois équations en trois variables. Nous commençons par résoudre la deuxième équation\(λ\) et la substituer dans la première équation. Cela donne\(λ=4y_0+4\), donc le substituer dans la première équation donne la\[2x_0−2=4y_0+4.\nonumber \] résolution de cette équation pour\(x_0\) donne\(x_0=2y_0+3\). Nous la substituons ensuite à la troisième équation :
\[\begin{align*} (2y_0+3)+2y_0−7 =0 \\[4pt]4y_0−4 =0 \\[4pt]y_0 =1. \end{align*}\]
Puisque\(x_0=2y_0+3,\) cela donne\(x_0=5.\)
4. Ensuite, nous évaluons\(f(x,y)=x^2+4y^2−2x+8y\) au point\((5,1)\).\[f(5,1)=5^2+4(1)^2−2(5)+8(1)=27. \nonumber \] Pour nous assurer que cela correspond à une valeur minimale de la fonction de contrainte, essayons d'autres points de la contrainte de chaque côté du point\((5,1)\), tels que les interceptions de\(g(x,y)=0\), Qui sont\((7,0)\) et\((0,3.5)\).
Nous obtenons\(f(7,0)=35 \gt 27\) et\(f(0,3.5)=77 \gt 27\).
Il apparaît donc qu'il\(f\) a un minimum relatif de\(27\) at\((5,1)\), sous réserve de la contrainte donnée.
Utilisez la méthode des multiplicateurs de Lagrange pour déterminer la valeur maximale de
\[f(x,y)=9x^2+36xy−4y^2−18x−8y \nonumber \]
sous réserve de la contrainte\(3x+4y=32.\)
- Allusion
-
Utilisez la stratégie de résolution de problèmes pour la méthode des multiplicateurs de Lagrange.
- Réponse
-
Sous réserve de la contrainte donnée,\(f\) a une valeur maximale de\(976\) au point\((8,2)\).
Revenons maintenant au problème posé au début de la section.
Le fabricant de balles de golf, Pro-T, a développé un modèle de profit qui dépend\(x\) du nombre de balles de golf vendues par mois (mesuré en milliers) et du nombre d'heures de publicité par mois, selon la fonction
\[z=f(x,y)=48x+96y−x^2−2xy−9y^2, \nonumber \]
où elle\(z\) est mesurée en milliers de dollars. La fonction de contrainte budgétaire reliant le coût de production de milliers de balles de golf et d'unités publicitaires est donnée par\(20x+4y=216.\) Trouvez les valeurs de\(x\) et\(y\) qui maximisent le profit, et trouvez le profit maximum.
Solution :
Encore une fois, nous suivons la stratégie de résolution des problèmes :
- La fonction objective est\(f(x,y)=48x+96y−x^2−2xy−9y^2.\) Pour déterminer la fonction de contrainte, nous\(216\) soustrayons d'abord des deux côtés de la contrainte, puis nous divisons les deux côtés par\(4\), ce qui donne\(5x+y−54=0.\) La fonction de contrainte est égale au côté gauche, donc\(g(x,y)=5x+y−54.\) Le problème nous demande de résoudre valeur maximale de\(f\), sous réserve de cette contrainte.
- Donc, nous calculons les gradients des deux\(f\) et\(g\) :\[\begin{align*} \vecs ∇f(x,y) &=(48−2x−2y)\hat{\mathbf i}+(96−2x−18y)\hat{\mathbf j}\\[4pt]\vecs ∇g(x,y) &=5\hat{\mathbf i}+\hat{\mathbf j}. \end{align*}\] L'équation\(\vecs ∇f(x_0,y_0)=λ\vecs ∇g(x_0,y_0)\) devient\[(48−2x_0−2y_0)\hat{\mathbf i}+(96−2x_0−18y_0)\hat{\mathbf j}=λ(5\hat{\mathbf i}+\hat{\mathbf j}),\nonumber \] qui peut être réécrite au fur et à mesure que\[(48−2x_0−2y_0)\hat{\mathbf i}+(96−2x_0−18y_0)\hat{\mathbf j}=λ5\hat{\mathbf i}+λ\hat{\mathbf j}.\nonumber \] nous définissons les coefficients\(\hat{\mathbf i}\) et\(\hat{\mathbf j}\) égaux les uns aux autres :\[\begin{align*} 48−2x_0−2y_0 =5λ \\[4pt] 96−2x_0−18y_0 =λ. \end{align*}\] L'équation\(g(x_0,y_0)=0\) devient\(5x_0+y_0−54=0\). Par conséquent, le système d'équations à résoudre est\[\begin{align*} 48−2x_0−2y_0 =5λ \\[4pt] 96−2x_0−18y_0 =λ \\[4pt]5x_0+y_0−54 =0. \end{align*}\]
- Nous utilisons le côté gauche de la deuxième équation pour remplacer\(λ\) dans la première équation :\[\begin{align*} 48−2x_0−2y_0 &=5(96−2x_0−18y_0) \\[4pt]48−2x_0−2y_0 &=480−10x_0−90y_0 \\[4pt] 8x_0 &=432−88y_0 \\[4pt] x_0 &=54−11y_0. \end{align*}\] Ensuite, nous la substituons dans la troisième équation :\[\begin{align*} 5(54−11y_0)+y_0−54 &=0\\[4pt] 270−55y_0+y_0-54 &=0\\[4pt]216−54y_0 &=0 \\[4pt]y_0 &=4. \end{align*}\] Puisque\(x_0=54−11y_0,\) cela donne\(x_0=10.\)
- Nous substituons\((10,4)\) ensuite\(f(x,y)=48x+96y−x^2−2xy−9y^2,\) ce qui donne.\[\begin{align*} f(10,4) &=48(10)+96(4)−(10)^2−2(10)(4)−9(4)^2 \\[4pt] &=480+384−100−80−144 \\[4pt] &=540.\end{align*}\] Par conséquent, le profit maximal qui peut être atteint, sous réserve de contraintes budgétaires, est\($540,000\) avec un niveau de production de balles de\(10,000\) golf et des\(4\) heures de publicité achetées par mois. Vérifions-en pour nous assurer que c'est vraiment un maximum. Les extrémités de la ligne qui définit la contrainte sont\((10.8,0)\) et\((0,54)\) évaluons\(f\) à ces deux points :\[\begin{align*} f(10.8,0) &=48(10.8)+96(0)−10.8^2−2(10.8)(0)−9(0^2) \\[4pt] &=401.76 \\[4pt] f(0,54) &=48(0)+96(54)−0^2−2(0)(54)−9(54^2) \\[4pt] &=−21,060. \end{align*}\] La deuxième valeur représente une perte, puisqu'aucune balle de golf n'est produite. Aucune de ces valeurs ne dépasse\(540\), il semble donc que notre extremum soit une valeur maximale de\(f\), sous réserve de la contrainte donnée.
Une entreprise a déterminé que son niveau de production est donné par la fonction Cobb-Douglas\(f(x,y)=2.5x^{0.45}y^{0.55}\),\(x\) qui représente le nombre total d'heures de travail par\(1\) an et\(y\) représente l'apport total en capital de l'entreprise. Supposons\(1\) l'unité des coûts de main-d'œuvre\($40\) et\(1\) l'unité des coûts d'investissement\($50\). Utilisez la méthode des multiplicateurs de Lagrange pour déterminer la valeur maximale de l'\(f(x,y)=2.5x^{0.45}y^{0.55}\)objet soumis à une contrainte\($500,000\) budgétaire annuelle.
- Allusion
-
Utilisez la stratégie de résolution de problèmes pour la méthode des multiplicateurs de Lagrange.
- Réponse
-
Sous réserve de la contrainte donnée, un niveau de production maximal de\(13890\) se produit en fonction des heures de\(5625\) travail et\($5500\) de l'apport total de capital.
Dans le cas d'une fonction objective à trois variables et une seule fonction de contrainte, il est également possible d'utiliser la méthode des multiplicateurs de Lagrange pour résoudre un problème d'optimisation. Un exemple de fonction objective à trois variables pourrait être la fonction Cobb-Douglas dans Exercise\(\PageIndex{2}\) :\(f(x,y,z)=x^{0.2}y^{0.4}z^{0.4},\) où\(x\) représente le coût de la main-d'œuvre,\(y\) représente l'apport en capital et\(z\) représente le coût de la publicité. La méthode est la même que pour la méthode avec une fonction de deux variables ; les équations à résoudre sont
\[\begin{align*} \vecs ∇f(x,y,z) &=λ\vecs ∇g(x,y,z) \\[4pt] g(x,y,z) &=0. \end{align*}\]
Maximiser la fonction\(f(x,y,z)=x^2+y^2+z^2\) soumise à la contrainte\(x+y+z=1.\)
Solution
1. La fonction objective est\(f(x,y,z)=x^2+y^2+z^2.\) Pour déterminer la fonction de contrainte, nous la soustrayons\(1\) de chaque côté de la contrainte :\(x+y+z−1=0\) ce qui donne à la fonction de contrainte\(g(x,y,z)=x+y+z−1.\)
2. Ensuite, nous calculons\(\vecs ∇f(x,y,z)\) et\(\vecs ∇g(x,y,z):\)\[\begin{align*} \vecs ∇f(x,y,z) &=⟨2x,2y,2z⟩ \\[4pt] \vecs ∇g(x,y,z) &=⟨1,1,1⟩. \end{align*}\] cela conduit aux équations\[\begin{align*} ⟨2x_0,2y_0,2z_0⟩ &=λ⟨1,1,1⟩ \\[4pt] x_0+y_0+z_0−1 &=0 \end{align*}\] qui peuvent être réécrites sous la forme suivante :\[\begin{align*} 2x_0 &=λ\\[4pt] 2y_0 &=λ \\[4pt] 2z_0 &=λ \\[4pt] x_0+y_0+z_0−1 &=0. \end{align*}\]
3. Comme chacune des trois premières équations se\(λ\) trouve sur le côté droit, nous le savons\(2x_0=2y_0=2z_0\) et les trois variables sont égales les unes aux autres. En substituant\(y_0=x_0\) et\(z_0=x_0\) dans la dernière équation, on obtient\(3x_0−1=0,\) ainsi\(x_0=\frac{1}{3}\)\(y_0=\frac{1}{3}\) et\(z_0=\frac{1}{3}\) ce qui correspond à un point critique de la courbe de contrainte.
4. Ensuite, nous évaluons\(f\) au point suivant\(\left(\frac{1}{3},\frac{1}{3},\frac{1}{3}\right)\) :\[f\left(\frac{1}{3},\frac{1}{3},\frac{1}{3}\right)=\left(\frac{1}{3}\right)^2+\left(\frac{1}{3}\right)^2+\left(\frac{1}{3}\right)^2=\dfrac{3}{9}=\dfrac{1}{3} \nonumber \] Par conséquent, un extremum possible de la fonction est\(\frac{1}{3}\). Pour vérifier qu'il s'agit d'un minimum, choisissez d'autres points qui satisfont à la contrainte de chaque côté du point que nous avons obtenu ci-dessus et calculez\(f\) à ces points. Par exemple, ces\[\begin{align*} f(1,0,0) &=1^2+0^2+0^2=1 \\[4pt] f(0,−2,3) &=0^2++(−2)^2+3^2=13. \end{align*}\] deux valeurs sont supérieures à\(\frac{1}{3}\), ce qui nous amène à penser que l'extremum est un minimum, sous réserve de la contrainte donnée.
Utilisez la méthode des multiplicateurs de Lagrange pour trouver la valeur minimale de la fonction
\[f(x,y,z)=x+y+z \nonumber \]
sous réserve de la contrainte\(x^2+y^2+z^2=1.\)
- Allusion
-
Utilisez la stratégie de résolution de problèmes pour la méthode des multiplicateurs de Lagrange avec une fonction objective de trois variables.
- Réponse
-
L'évaluation\(f\) aux deux points que nous avons obtenus nous donne,\[\begin{align*} f\left(\dfrac{\sqrt{3}}{3},\dfrac{\sqrt{3}}{3},\dfrac{\sqrt{3}}{3}\right) =\dfrac{\sqrt{3}}{3}+\dfrac{\sqrt{3}}{3}+\dfrac{\sqrt{3}}{3}=\sqrt{3} \\ f\left(−\dfrac{\sqrt{3}}{3},−\dfrac{\sqrt{3}}{3},−\dfrac{\sqrt{3}}{3}\right) =−\dfrac{\sqrt{3}}{3}−\dfrac{\sqrt{3}}{3}−\dfrac{\sqrt{3}}{3}=−\sqrt{3}\end{align*}\] Puisque la contrainte est continue, nous comparons ces valeurs et concluons que cela\(f\) a un minimum relatif\(−\sqrt{3}\) au point\(\left(−\dfrac{\sqrt{3}}{3},−\dfrac{\sqrt{3}}{3},−\dfrac{\sqrt{3}}{3}\right)\), sous réserve de la contrainte donnée.
Problèmes liés à deux contraintes
La méthode des multiplicateurs de Lagrange peut être appliquée à des problèmes comportant plus d'une contrainte. Dans ce cas, la fonction objective\(w\) est fonction de trois variables :
\[w=f(x,y,z) \nonumber \]
et elle est soumise à deux contraintes :
\[g(x,y,z)=0 \; \text{and} \; h(x,y,z)=0. \nonumber \]
Il existe deux multiplicateurs de Lagrange\(λ_2\),\(λ_1\) et le système d'équations devient
\[\begin{align*} \vecs ∇f(x_0,y_0,z_0) &=λ_1\vecs ∇g(x_0,y_0,z_0)+λ_2\vecs ∇h(x_0,y_0,z_0) \\[4pt] g(x_0,y_0,z_0) &=0\\[4pt] h(x_0,y_0,z_0) &=0 \end{align*}\]
Trouvez les valeurs maximale et minimale de la fonction
\[f(x,y,z)=x^2+y^2+z^2 \nonumber \]
sous réserve des contraintes\(z^2=x^2+y^2\) et\(x+y−z+1=0.\)
Solution
Suivons la stratégie de résolution des problèmes :
- La fonction objective est\(f(x,y,z)=x^2+y^2+z^2.\) Pour déterminer les fonctions de contrainte, nous\(z^2\) soustrayons d'abord des deux côtés de la première contrainte, ce qui donne\(x^2+y^2−z^2=0\) donc\(g(x,y,z)=x^2+y^2−z^2\). La deuxième fonction de contrainte est\(h(x,y,z)=x+y−z+1.\)
- Nous calculons ensuite les gradients de\(f,g,\) et\(h\) :\[\begin{align*} \vecs ∇f(x,y,z) &=2x\hat{\mathbf i}+2y\hat{\mathbf j}+2z\hat{\mathbf k} \\[4pt] \vecs ∇g(x,y,z) &=2x\hat{\mathbf i}+2y\hat{\mathbf j}−2z\hat{\mathbf k} \\[4pt] \vecs ∇h(x,y,z) &=\hat{\mathbf i}+\hat{\mathbf j}−\hat{\mathbf k}. \end{align*}\] L'équation\(\vecs ∇f(x_0,y_0,z_0)=λ_1\vecs ∇g(x_0,y_0,z_0)+λ_2\vecs ∇h(x_0,y_0,z_0)\) devient\[2x_0\hat{\mathbf i}+2y_0\hat{\mathbf j}+2z_0\hat{\mathbf k}=λ_1(2x_0\hat{\mathbf i}+2y_0\hat{\mathbf j}−2z_0\hat{\mathbf k})+λ_2(\hat{\mathbf i}+\hat{\mathbf j}−\hat{\mathbf k}), \nonumber \] qui peut être réécrite comme\[2x_0\hat{\mathbf i}+2y_0\hat{\mathbf j}+2z_0\hat{\mathbf k}=(2λ_1x_0+λ_2)\hat{\mathbf i}+(2λ_1y_0+λ_2)\hat{\mathbf j}−(2λ_1z_0+λ_2)\hat{\mathbf k}. \nonumber \] suit, nous définissons les coefficients de\(\hat{\mathbf i}\) et\(\hat{\mathbf j}\) égaux l'un à l'autre :\[\begin{align*}2x_0 &=2λ_1x_0+λ_2 \\[4pt]2y_0 &=2λ_1y_0+λ_2 \\[4pt]2z_0 &=−2λ_1z_0−λ_2. \end{align*}\] Les deux équations qui découlent des contraintes sont \(z_0^2=x_0^2+y_0^2\)et\(x_0+y_0−z_0+1=0\). La combinaison de ces équations avec les trois équations précédentes donne\[\begin{align*} 2x_0 &=2λ_1x_0+λ_2 \\[4pt]2y_0 &=2λ_1y_0+λ_2 \\[4pt]2z_0 &=−2λ_1z_0−λ_2 \\[4pt]z_0^2 &=x_0^2+y_0^2 \\[4pt]x_0+y_0−z_0+1 &=0. \end{align*}\]
- Les trois premières équations contiennent la variable\(λ_2\). La résolution de la troisième équation\(λ_2\) et la remplacement dans les première et deuxième équations réduisent le nombre d'équations à quatre :\[\begin{align*}2x_0 &=2λ_1x_0−2λ_1z_0−2z_0 \\[4pt] 2y_0 &=2λ_1y_0−2λ_1z_0−2z_0\\[4pt] z_0^2 &=x_0^2+y_0^2\\[4pt] x_0+y_0−z_0+1 &=0. \end{align*}\] Ensuite, nous résolvons la première et la deuxième équation pour\(λ_1\). La première équation donne\(λ_1=\dfrac{x_0+z_0}{x_0−z_0}\), la deuxième donne\(λ_1=\dfrac{y_0+z_0}{y_0−z_0}\). Nous mettons le côté droit de chaque équation égal l'un à l'autre et multiplions de manière croisée :\[\begin{align*} \dfrac{x_0+z_0}{x_0−z_0} &=\dfrac{y_0+z_0}{y_0−z_0} \\[4pt](x_0+z_0)(y_0−z_0) &=(x_0−z_0)(y_0+z_0) \\[4pt]x_0y_0−x_0z_0+y_0z_0−z_0^2 &=x_0y_0+x_0z_0−y_0z_0−z_0^2 \\[4pt]2y_0z_0−2x_0z_0 &=0 \\[4pt]2z_0(y_0−x_0) &=0. \end{align*}\] Par conséquent, soit\(z_0=0\) ou\(y_0=x_0\). Si\(z_0=0\), alors la première contrainte devient\(0=x_0^2+y_0^2\). La seule vraie solution à cette équation est\(x_0=0\) et\(y_0=0\), qui donne le triple ordonné\((0,0,0)\). Ce point ne satisfait pas à la deuxième contrainte, il ne s'agit donc pas d'une solution. Ensuite, nous considérons\(y_0=x_0\), ce qui réduit le nombre d'équations à trois :\[\begin{align*}y_0 &= x_0 \\[4pt] z_0^2 &= x_0^2 +y_0^2 \\[4pt] x_0 + y_0 -z_0+1 &=0. \end{align*} \nonumber \] Nous substituons la première équation par les deuxième et troisième équations :\[\begin{align*} z_0^2 &= x_0^2 +x_0^2 \\[4pt] &= x_0+x_0-z_0+1 &=0. \end{align*} \nonumber \] Ensuite, nous résolvons la deuxième équation pour\(z_0\), qui donne\(z_0=2x_0+1\). Nous la substituons ensuite dans la première équation\[\begin{align*} z_0^2 &= 2x_0^2 \\[4pt] (2x_0^2 +1)^2 &= 2x_0^2 \\[4pt] 4x_0^2 + 4x_0 +1 &= 2x_0^2 \\[4pt] 2x_0^2 +4x_0 +1 &=0, \end{align*}\] et utilisons la formule quadratique pour résoudre\(x_0\) :\[ x_0 = \dfrac{-4 \pm \sqrt{4^2 -4(2)(1)} }{2(2)} = \dfrac{-4\pm \sqrt{8}}{4} = \dfrac{-4 \pm 2\sqrt{2}}{4} = -1 \pm \dfrac{\sqrt{2}}{2}. \nonumber \] Rappelez-vous\(y_0=x_0\), donc cela résout\(y_0\) également pour. Alors\(z_0=2x_0+1\),\[z_0 = 2x_0 +1 =2 \left( -1 \pm \dfrac{\sqrt{2}}{2} \right) +1 = -2 + 1 \pm \sqrt{2} = -1 \pm \sqrt{2} . \nonumber \] donc, il existe deux solutions triplet ordonnées :\[\left( -1 + \dfrac{\sqrt{2}}{2} , -1 + \dfrac{\sqrt{2}}{2} , -1 + \sqrt{2} \right) \; \text{and} \; \left( -1 -\dfrac{\sqrt{2}}{2} , -1 -\dfrac{\sqrt{2}}{2} , -1 -\sqrt{2} \right). \nonumber \]
- Nous\(\left(−1+\dfrac{\sqrt{2}}{2},−1+\dfrac{\sqrt{2}}{2}, −1+\sqrt{2}\right) \) substituons par\(f(x,y,z)=x^2+y^2+z^2\), ce qui donne\[\begin{align*} f\left( -1 + \dfrac{\sqrt{2}}{2}, -1 + \dfrac{\sqrt{2}}{2} , -1 + \sqrt{2} \right) &= \left( -1+\dfrac{\sqrt{2}}{2} \right)^2 + \left( -1 + \dfrac{\sqrt{2}}{2} \right)^2 + (-1+\sqrt{2})^2 \\[4pt] &= \left( 1-\sqrt{2}+\dfrac{1}{2} \right) + \left( 1-\sqrt{2}+\dfrac{1}{2} \right) + (1 -2\sqrt{2} +2) \\[4pt] &= 6-4\sqrt{2}. \end{align*}\] Ensuite, nous\(\left(−1−\dfrac{\sqrt{2}}{2}, -1+\dfrac{\sqrt{2}}{2}, -1+\sqrt{2}\right)\) substituons par\(f(x,y,z)=x^2+y^2+z^2\), qui donne\[\begin{align*} f\left(−1−\dfrac{\sqrt{2}}{2}, -1+\dfrac{\sqrt{2}}{2}, -1+\sqrt{2} \right) &= \left( -1-\dfrac{\sqrt{2}}{2} \right)^2 + \left( -1 - \dfrac{\sqrt{2}}{2} \right)^2 + (-1-\sqrt{2})^2 \\[4pt] &= \left( 1+\sqrt{2}+\dfrac{1}{2} \right) + \left( 1+\sqrt{2}+\dfrac{1}{2} \right) + (1 +2\sqrt{2} +2) \\[4pt] &= 6+4\sqrt{2}. \end{align*}\]\(6+4\sqrt{2}\) est la valeur maximale et\(6−4\sqrt{2}\) est la valeur minimale de\(f(x,y,z)\), sous réserve des contraintes données.
Utilisez la méthode des multiplicateurs de Lagrange pour trouver la valeur minimale de la fonction
\[f(x,y,z)=x^2+y^2+z^2 \nonumber \]
sous réserve des contraintes\(2x+y+2z=9\) et\(5x+5y+7z=29.\)
- Allusion
-
Utilisez la stratégie de résolution de problèmes pour la méthode des multiplicateurs de Lagrange avec deux contraintes.
- Réponse
-
\(f(2,1,2)=9\)est une valeur minimale de\(f\), sous réserve des contraintes données.
Concepts clés
- Une fonction objective combinée à une ou plusieurs contraintes est un exemple de problème d'optimisation.
- Pour résoudre les problèmes d'optimisation, nous appliquons la méthode des multiplicateurs de Lagrange en utilisant une stratégie de résolution des problèmes en quatre étapes.
Équations clés
- Méthode des multiplicateurs de Lagrange, une contrainte
\(\vecs ∇f(x_0,y_0)=λ\vecs ∇g(x_0,y_0)\)
\(g(x_0,y_0)=0\)
- Méthode des multiplicateurs de Lagrange, deux contraintes
\(\vecs ∇f(x_0,y_0,z_0)=λ_1\vecs ∇g(x_0,y_0,z_0)+λ_2\vecs ∇h(x_0,y_0,z_0)\)
\(g(x_0,y_0,z_0)=0\)
\(h(x_0,y_0,z_0)=0\)
Lexique
- contrainte
- une inégalité ou une équation impliquant une ou plusieurs variables qui est utilisée dans un problème d'optimisation ; la contrainte impose une limite aux solutions possibles au problème
- multiplicateur Lagrange
- la constante (ou les constantes) utilisée dans la méthode des multiplicateurs de Lagrange ; dans le cas d'une constante, elle est représentée par la variable\(λ\)
- méthode des multiplicateurs de Lagrange
- une méthode pour résoudre un problème d'optimisation soumis à une ou plusieurs contraintes
- fonction objective
- la fonction qui doit être maximisée ou minimisée dans un problème d'optimisation
- problème d'optimisation
- calcul d'une valeur maximale ou minimale d'une fonction de plusieurs variables, souvent à l'aide de multiplicateurs de Lagrange


