14.7E : Exercices pour la section 14.7

Last updated
Save as PDF

Page ID: 197370

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Trouver des points critiques

Dans les exercices 1 à 5, trouvez tous les points critiques.

1)$ f(x,y)=1+x^2+y^2$

Réponse: $ (0,0)$

2)$ f(x, y) = 1 - (x -2)^2 + (y+3)^2$

3)$ f(x,y)=(3x−2)^2+(y−4)^2$

Réponse: $ \left(\frac{2}{3},4\right)$

4)$ f(x,y)=x^4+y^4−16xy$

Réponse: $ (0,0), \quad (-2,-2), \quad (2,2)$

5)$ f(x,y)=15x^3−3xy+15y^3$

Réponse: $ (0,0), \quad \left(\frac{1}{15},\frac{1}{15}\right)$

Finding Extrema et le deuxième critère des partiels

Dans les exercices 6 à 9, trouvez les points critiques de la fonction et testez les extrêmes ou les points de selle en utilisant des techniques algébriques (complétant le carré) ou en examinant la forme de l'équation. Dans la mesure du possible, vérifiez vos résultats à l'aide du deuxième test partiel.

6)$ f(x,y)=-\sqrt{x^2+y^2}$

Réponse: Critique. pts. :$ (0, 0) $
Extrema :$ f$ a un maximum relatif de$0$ at$ (0, 0)$.
Pour justifier cela, considérez le fait que la fonction de racine carrée ne peut pas donner de valeur négative, de sorte que cette fonction ne peut pas renvoyer de valeur positive. Comme sa valeur est$0$ au point critique$ (0, 0)$, nous savons qu'il doit s'agir de la valeur maximale absolue de la fonction.

7)$ f(x,y)=−x^2−5y^2+8x−10y−13$

Réponse: Critique. pts. :$ (4, -1) $
Extrema :$ f$ a un maximum relatif de$8$ at$ (4,−1)$.
Pour justifier cela, nous complétons le carré sur cette fonction, en prenant soin de prendre en compte le coefficient des termes au carré avant de compléter le carré.
\[\begin{align*} f(x, y) &= −x^2−5y^2+8x−10y−13 \\ &= −(x^2-8x\quad\quad)−5(y^2+2y\quad\quad)−13 \\ &= −(x^2-8x+16)−5(y^2+2y+1)−13+16+5 \\ &= -(x-4)^2 -5(y+1)^2+8\end{align*}\]
Notez que cette fonction polynomiale quadratique prend la forme$ z = -(x^2 + y^2)$, nous pouvons donc voir qu'elle aura un maximum relatif (et, en fait, absolu) à son sommet (le point critique$ (4, -1) $). Nous pouvons également faire valoir que puisque nous soustrayons des termes au carré de 8, nous ne pouvons pas obtenir une valeur de fonction supérieure à 8, et comme nous obtenons une valeur de 8 au point critique$ (4, -1) $, nous savons que ce sera la valeur maximale absolue de cette fonction.

8)$ f(x,y)=x^2+y^2+2x−6y+6$

9)$ f(x,y)=\sqrt{x^2+y^2}+1$

Réponse: Crit. Points :$ (0, 0) $
Extrema :$ f$ possède un minimum relatif de$1$ at$ (0,0)$.
Pour justifier cela, considérez le fait que la fonction de racine carrée ne peut pas donner de valeur négative, de sorte que cette fonction ne peut pas renvoyer une valeur inférieure à$1$. Comme sa valeur est$1$ au point critique$ (0, 0)$, nous savons qu'il$1$ doit s'agir de la valeur minimale absolue de la fonction.

Dans les exercices 10 à 34, identifiez les points critiques et utilisez le test Second Patials pour déterminer le comportement de la fonction à chaque point critique, s'il existe un maximum, un minimum, un point de selle ou aucun de ces points. Si le deuxième test partiel échoue, déterminez le comportement de la fonction à ce stade en utilisant une autre méthode et justifiez clairement votre réponse.

10)$ f(x,y)=−x^3+4xy−2y^2+1$

11)$ f(x,y)=x^2y^2$

Réponse: Points critiques : Tous les points sur les lignes$ y = 0$ sont$ x = 0 $ des points critiques de cette fonction.
Exrema : Le deuxième test partiel échoue.
Puisque$ x^2y^2>0$ pour tous$ x$ et$ y$ différemment de zéro, et$ x^2y^2=0$ lorsque l'un$ x$ ou l'autre$ y$ est égal à zéro (ou les deux), alors le minimum absolu de$0$ se produit en tous les points sur les$y$ axes$x$ - ou -, c'est-à-dire pour tous les points du lignes$ x = 0 $ et$ y = 0$.

(12)$ f(x,y)=x^2−6x+y^2+4y−8$

13)$ f(x,y)=2xy+3x+4y$

Réponse: Critique. points :$ \left(−2,−\frac{3}{2}\right) $
$f$ Exrema : possède un point de selle à$ \left(−2,−\frac{3}{2},−6\right) $.

(14)$ f(x,y)=8xy(x+y)+7$

(15)$ f(x,y)=x^2+4xy+y^2$

Réponse: Critique. points :$ (0,0) $
$f$ Exrema : possède un point de selle à$ (0,0,0)$.

16)$ f(x,y)=x^3+y^3−300x−75y−3$

17)$ f(x,y)=9−x^4y^4$

Réponse: Points critiques : Tous les points sur les lignes$ y = 0$ sont$ x = 0 $ des points critiques de cette fonction.
Extrema : Le deuxième test partiel échoue.
Puisque le terme$ -x^4y^4<0$ désignant tous$ x$ est$ y$ différent de zéro, et$ -x^4y^4=0$ lorsque l'un$ x$ ou l'autre$ y$ est égal à zéro (ou les deux), cette fonction ne peut pas atteindre une valeur supérieure$9$ à$9$ n'importe laquelle, mais se situe aux points critiques. Il$f$ a donc un maximum absolu de$9$ en tous les points des$y$ axes$x$ - ou -, c'est-à-dire pour tous les points des lignes$ x = 0 $ et$ y = 0$.

18)$ f(x,y)=x^2+10xy+y^2$

Réponse: Critique. pts. :$ (0,0) $
Extrema :$f$ a un point de selle à$ (0,0,0)$.

19)$f(x,y) = x^4 + y^2 + 2xy + 3$

Réponse: Points critiques :$ (0,0), \quad \left(-\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2}\right), \quad \left(\frac{\sqrt{2}}{2}, -\frac{\sqrt{2}}{2}\right) $
Extrema :$f$ a un point de selle à$ (0, 0, 3) $,
$f$ a un minimum local de$ 2.75$ au point$ \left(-\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2}\right) $.
$f$a un minimum local de$ 2.75$ au point$ \left(\frac{\sqrt{2}}{2}, -\frac{\sqrt{2}}{2}\right) $.

(20)$ f(x,y)=7x^2y+9xy^2$

(21)$ f(x,y)=3x^2−2xy+y^2−8y$

Réponse: Critique. pts. :$ (2,6) $
Extrema :$f$ a un minimum relatif de$ -24$ situé à$ (2,6)$.

(22)$ f(x,y)=3x^2+2xy+y^2$

23)$ f(x,y)=y^2+xy+3y+2x+3$

Réponse: Critique. pts. :$ (1,−2) $
Extrema :$f$ a un point de selle à$ (1,−2,1)$.

(24)$ f(x,y)=x^2+xy+y^2−3x$

25)$ f(x,y)=x^2+2y^2−x^2y$

Réponse: Points critiques :$ (0,0), \quad (-2,1), \quad (2,1)$
Extrema :$f$ a un minimum relatif d'$0$at$ (0,0) $ et de points de selle à$ (2,1,2)$ et$ (−2,1,2)$.

(26)$ f(x,y)=x^2+y−e^y$

(27)$ f(x,y)=e^{−(x^2+y^2+2x)}$

Réponse: Critique. pts. :$ (-1,0) $
Extrema :$f$ a un maximum relatif de$ e $ situé à$ (-1,0)$.
Voir ce problème illustré dans CalcPlot3D.

(28)$ f(x,y)=x^2+xy+y^2−x−y+1$

(29)$f(x,y) = x^2y(9 - x + y)$

Réponse: Critique. pts. :$ \left(\frac{9}{2},-\frac{9}{4}\right), \quad (9,0)$, et tous les points de la ligne$x = 0$
Extrema :$f$ ont un point de selle$ (9,0,0)$ et un minimum relatif de$-102.515625$ at$ \left(\frac{9}{2},-\frac{9}{4}\right)$.
Aux points critiques de la ligne$x = 0$, il n'y$f$ a ni extrêmes relatifs ni points de selle, mais ils représentent une sorte de creux à la surface.

(30)$ f(x,y)=−x^2−5y^2+10x−30y−62$

31)$ f(x,y)=120x+120y−xy−x^2−y^2$

Réponse: Critique. pts. :$ (40,40) $
Extrema :$f$ a un maximum relatif de$ 4800 $ situé à$ (40,40)$.

32)$ f(x,y)=2x^2+2xy+y^2+2x−3$

33)$ f(x,y)=x^2+x−3xy+y^3−5$

Réponse: Crit. pts. :$ \left(\frac{1}{4},\frac{1}{2}\right)$ et$(1, 1) $
Extrema :$f$ a un point de selle à$ \left(\frac{1}{4},\frac{1}{2}, -\frac{79}{16}\right)$ et un minimum relatif de$ -5 $ at$ (1,1)$.

34)$ f(x,y)=2xye^{−x^2−y^2}$

Dans les exercices 35 à 37, déterminez les valeurs extrêmes et les points de selle. Utilisez un CAS pour représenter graphiquement la fonction.

35) [T]$ f(x,y)=ye^x−e^y$

Réponse

Un point de selle est situé à$ (0,0,-1).$

36) [T]$ f(x,y)=x\sin(y)$

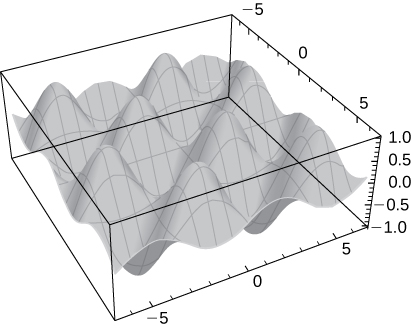
37) [T]$ f(x,y)=\sin(x)\sin(y),\quad x∈(0,2π),\quad y∈(0,2π)$

Réponse

Il y a un point de selle$ (π,π),$ aux maxima locaux à$ \left(\frac{π}{2},\frac{π}{2}\right)$ et$ \left(\frac{3π}{2},\frac{3π}{2}\right)$, et des minima locaux à$ \left(\frac{π}{2},\frac{3π}{2}\right)$ et$ \left(\frac{3π}{2},\frac{π}{2}\right)$.

$Diagramme de surface de la fonction f (x, y) = sin (x) sin (y)$

Dans les exercices 38 à 41, trouvez les extrêmes absolus de la fonction donnée sur l'ensemble fermé et borné indiqué$R$.

38)$f(x,y)=xy−x−3y$ où$R$ est la région triangulaire avec des sommets$(0,0), \, (0,4),$ et$(5,0)$.

39) Trouvez les valeurs maximales et minimales absolues de$f(x,y)=x^2+y^2−2y+1$ sur la région$R=\big\{(x,y) \, | \, x^2+y^2≤4\big\}.$

Réponse: $(0,1,0)$est le minimum absolu et$(0,−2,9)$ le maximum absolu.

40)$f(x,y)=x^3−3xy−y^3$ sur$R=\big\{(x,y) \, | \, −2≤x≤2,\;−2≤y≤2\big\}$

41)$f(x,y)=\dfrac{−2y}{x^2+y^2+1}$ sur$R=\big\{(x,y) \, | \, x^2+y^2≤4\big\}$

Réponse: Il y a un minimum absolu à$(0,1,−1)$ et un maximum absolu à$(0,−1,1)$.

42) Trouvez trois nombres positifs dont la somme est égale à$27$, de telle sorte que la somme de leurs carrés soit aussi petite que possible.

43) Trouvez les points de la surface$x^2−yz=5$ les plus proches de l'origine.

Réponse: $\left(\sqrt{5},0,0\right), \; \left(−\sqrt{5},0,0\right)$

44) Détermine le volume maximum d'une boîte rectangulaire avec trois faces dans les plans de coordonnées et un sommet dans le premier octant de la ligne$x+y+z=1$.

45) La somme de la longueur et de la circonférence (périmètre d'une section transversale) d'un colis transporté par un service de livraison ne peut pas dépasser$108$ Trouvez les dimensions du colis rectangulaire du plus grand volume pouvant être envoyé.

Réponse: $18$par$36$ by$18$ in.

46) Une boîte en carton sans couvercle doit être fabriquée avec un volume de ^3$4$ pieds. Trouvez les dimensions de la boîte qui nécessite le moins de carton.

47) Trouvez le point sur la surface la$f(x,y)=x^2+y^2+10$ plus proche du plan$x+2y−z=0.$ Identifiez le point sur le plan.

Réponse: $\left(\frac{47}{24},\frac{47}{12},\frac{235}{24}\right)$

48) Trouvez le point dans le plan$2x−y+2z=16$ le plus proche de l'origine.

49) Une entreprise fabrique deux types de chaussures de sport : des chaussures de jogging et des chaussures de vélo elliptique. Le revenu total provenant des$x$ unités de chaussures de jogging et des$y$ unités de vélo elliptique est indiqué par$R(x,y)=−5x^2−8y^2−2xy+42x+102y,$ où$x$ et$y$ se situe en milliers d'unités. Déterminez les valeurs du chiffre$y$ d'affaires total$x$ et maximisez celui-ci.

Réponse: $x=3$et$y=6$

50) Une compagnie maritime manipule des boîtes rectangulaires à condition que la somme de la longueur, de la largeur et de la hauteur de la boîte ne dépasse pas$96$ pouces. Trouvez les dimensions de la boîte qui répond à cette condition et qui possède le plus grand volume.

51) Déterminez le volume maximum d'une canette de soda cylindrique de telle sorte que la somme de sa hauteur et de sa circonférence soit de$120$ cm.

Réponse: $V=\dfrac{64,000}{π}≈20,372\text{ cm}^3$

Contributeurs

Template:ContribOpenStaxCalc
Paul Seeburger (Monroe Community College) a créé les problèmes 19 et 29 et a ajouté des chiffres dynamiques pour les problèmes 27 et 35.