13.1E : Exercices pour la section 13.1
- Page ID
- 197221
Présentation des fonctions à valeur vectorielle
1) Donnez les fonctions du composant\(x=f(t)\) et\(y=g(t)\) pour la fonction à valeur vectorielle\(\vecs r(t)=3 \sec t \, \hat{\mathbf{i}}+2 \tan t \,\hat{\mathbf{j}}\).
- Réponse
- Ici, nous pouvons le dire\(f(t)=3 \sec t, \quad g(t)=2 \tan t\)
, nous l'avons fait\(x(t)=3 \sec t, \quad y(t)=2 \tan t\).
2) Étant donné\(\vecs r(t)=3 \sec t \hat{\mathbf{i}}+2 \tan t \hat{\mathbf{j}}\), trouvez les valeurs suivantes (si possible).
- \(\vecs r(\frac{\pi}{4})\)
- \(\vecs r(\pi)\)
- \(\vecs r(\frac{\pi}{2})\)
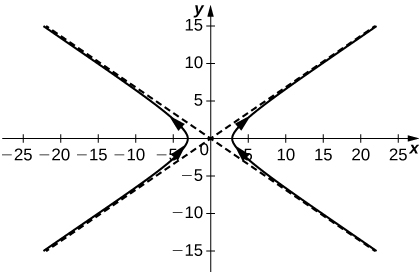
3) Esquissez la courbe de la fonction à valeur vectorielle\( \vecs r(t)=3 \sec t \hat{\mathbf{i}}+2 \tan t \hat{\mathbf{j}}\) et donnez l'orientation de la courbe. Esquissez des asymptotes pour vous orienter vers le graphique.
- Réponse
Limites des fonctions à valeur vectorielle
4) Évaluer\(\lim \limits_{t \to 0}\left(e^t \hat{\mathbf{i}}+\frac{\sin t}{t} \hat{\mathbf{j}}+e^{−t} \hat{\mathbf{k}}\right)\)
5) Étant donné la fonction à valeur vectorielle,\(\vecs r(t)=⟨\cos t,\sin t⟩\) trouvez les valeurs suivantes :
- \(\lim \limits_{t \to \frac{\pi}{4}} \vecs r(t)\)
- \(\vecs r(\frac{\pi}{3})\)
- Est-ce\(\vecs r(t)\) continu à\(t=\frac{\pi}{3}\) ?
- Graphe\(\vecs r(t)\).
- Réponse
-
a.\(⟨\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2}⟩\),
b.,
c. Oui\(⟨\frac{1}{2},\frac{\sqrt{3}}{2}⟩\), la limite à mesure que t\(\mathrm{\frac{\pi}{3}}\) s'approche est égale à\(\mathrm{r(\frac{\pi}{3})}\),
d.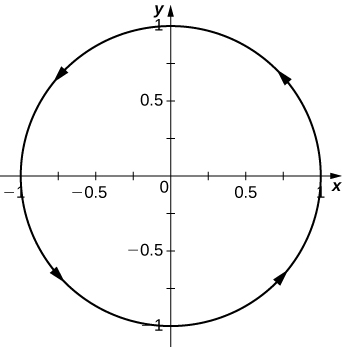
6) Étant donné la fonction à valeur vectorielle\(\vecs r(t)=⟨t,t^2+1⟩\), recherchez les valeurs suivantes :
- \(\lim \limits_{t \to -3} \vecs r(t)\)
- \(\vecs r(−3)\)
- Est-ce\(\vecs r(t)\) continu à\(x=−3\) ?
- \(\vecs r(t+2)−\vecs r(t)\)
7) Laissez\(\vecs r(t)=e^t \hat{\mathbf{i}}+\sin t \hat{\mathbf{j}}+\ln t \hat{\mathbf{k}}\). Trouvez les valeurs suivantes :
- \(\vecs r(\frac{\pi}{4})\)
- \(\lim \limits_{t \to \frac{\pi}{4} } \vecs r(t)\)
- Est-ce\(\vecs r(t)\) continu à\(t=\frac{\pi}{4}\) ?
- Réponse
- a. ⟩\(e^{\frac{\pi}{4}},\frac{\sqrt{2}}{2},\ln (\frac{\pi}{4})\) ⟩ ;
b. ⟩\(e^{\frac{\pi}{4}},\frac{\sqrt{2}}{2},\ln (\frac{\pi}{4})\) ⟩ ;
c. Oui
Pour les exercices 8 à 13, déterminez la limite des fonctions à valeur vectorielle suivantes à la valeur indiquée de\(t\).
8)\(\lim \limits_{t \to 4}⟨\sqrt{t−3},\frac{\sqrt{t}−2}{t−4},\tan(\frac{\pi}{t})⟩\)
9)\(\lim \limits_{t \to \frac{\pi}{2}} \vecs r(t)\) pour\(\vecs r(t)=e^t \hat{\mathbf{i}}+\sin t \hat{\mathbf{j}}+\ln t \hat{\mathbf{k}}\)
- Réponse
- \(⟨e^{\frac{\pi}{2}},1,\ln(\frac{\pi}{2})⟩\)
10)\(\lim \limits_{t \to \infty}⟨e^{−2t},\frac{2t+3}{3t−1},\arctan(2t)⟩\)
11)\(\lim \limits_{t \to e^2}⟨t \ln (t),\frac{\ln t}{t^2},\sqrt{\ln(t^2)⟩}\)
- Réponse
- \(2e^2 \hat{\mathbf{i}}+\frac{2}{e^4}\hat{\mathbf{j}}+2\hat{\mathbf{k}}\)
(12)\(\lim \limits_{t \to \frac{\pi}{6}}⟨\cos 2t,\sin 2t,1⟩\)
13)\(\lim \limits_{t \to \infty} \vecs r(t)\) pour\(\vecs r(t)=2e^{−t} \mathbf{ i}+e^{−t} \hat{\mathbf{j}}+\ln(t−1) \hat{\mathbf{k}}\)
- Réponse
- La limite n'existe pas parce que la limite de\(t\) l'\(\ln(t−1)\)infini n'existe pas.
Domaine d'une fonction à valeur vectorielle
Pour les problèmes 14 à 17, trouvez le domaine des fonctions à valeur vectorielle.
14) Domaine :\(\vecs r(t)=⟨t^2,t,\sin t⟩\)
15) Domaine :\(\vecs r(t)=⟨t^2,\tan t,\ln t⟩\)
- Réponse
- \(\text{D}_{\vecs r} = \left \{ t \,|\, t>0,t≠(2k+1)\frac{\pi}{2}, \, \text{where} \, k \,\text{is any integer} \right \}\)
16) Domaine :\(\vecs r(t)=⟨t^2,\sqrt{t−3},\frac{3}{2t+1}⟩\)
17) Domaine :\(\vecs r(t)=⟨\csc(t),\frac{1}{\sqrt{t−3}}, \ln(t−2)⟩\)
- Réponse
- \(\text{D}_{\vecs r} = \left \{ t \,|\, t>3,t≠n\pi, \, \text{where} \, n \,\text{is any integer} \right \}\)
18) a. Trouvez le domaine de\(\vecs r(t)=2e^{-t} \hat{\mathbf{i}}+e^{−t}\hat{\mathbf{j}}+\ln(t−1)\hat{\mathbf{k}}\).
b. Pour quelles valeurs de\(t\) est\(\vecs r(t)=2e^{-t} \hat{\mathbf{i}}+e^{−t}\hat{\mathbf{j}}+\ln(t−1)\hat{\mathbf{k}}\) continu ?
- Réponse
- a.\(\text{D}_{\vecs r}: ( 1, \infty )\)
b. Tout cela de\(t\) telle sorte que\(t∈(1,\infty)\)
19) Domaine :\(\vecs r(t)=(\arccos t) \, \hat{\mathbf{i}} + \sqrt{2t−1} \, \hat{\mathbf{j}}+\ln(t) \, \hat{\mathbf{k}}\)
- Réponse
- \(\text{D}_{\vecs r}: \big[ \frac{1}{2}, 1 \big]\)
Visualisation de fonctions à valeur vectorielle
20) Décrivez la courbe définie par la fonction à valeur vectorielle\(\vecs r(t)=(1+t)\hat{\mathbf{i}}+(2+5t)\hat{\mathbf{j}}+(−1+6t)\hat{\mathbf{k}}\).
21) Laissez-le\(\vecs r(t)=⟨\cos t,t,\sin t⟩\) et utilisez-le pour répondre aux questions suivantes.
- Pour quelles valeurs de\(t\) est\(\vecs r(t)\) continu ?
- Esquissez le graphique de\(\vecs r(t)\).
- Réponse
- a.\(\vecs r\) est continu pour tous les nombres réels, c'est-à-dire pour\(t \in \mathbb{R}\).
b. Notez qu'il doit y avoir un\(z\) sur l'axe vertical dans la coupe transversale de l'image (a) ci-dessous au lieu de\(y\).
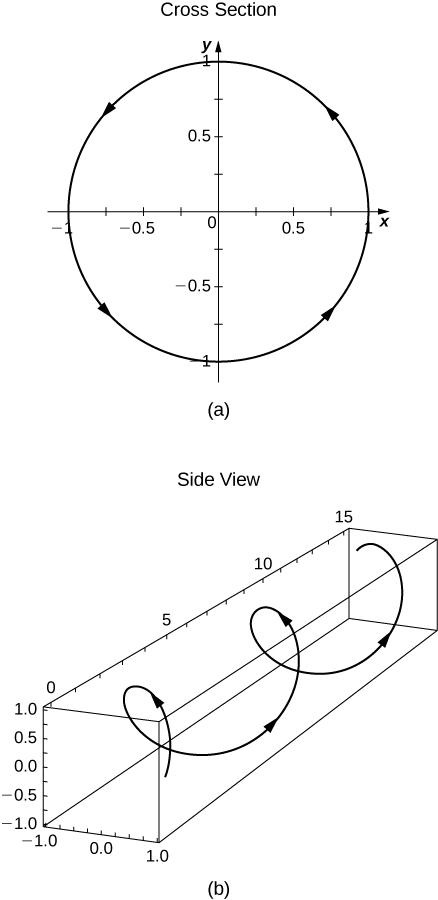
22) Produisez un croquis minutieux du graphique de\(\vecs r(t) = t^2 \, \hat{\mathbf{i}} + t \, \hat{\mathbf{j}}\).
Dans les questions 23 à 25, utilisez un utilitaire graphique pour esquisser chacune des fonctions à valeur vectorielle :
23) [T]\(\vecs r(t)=2 \cos^2 t \hat{\mathbf{i}}+(2−\sqrt{t})\hat{\mathbf{j}}\)
- Réponse
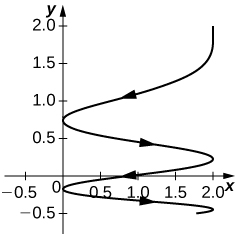
24) [T]\(\vecs r(t)=⟨e^{\cos (3t)},e^{−\sin(t)}⟩\)
25) [T]\(\vecs r(t)=⟨2−\sin (2t),3+2 \cos t⟩\)
- Réponse
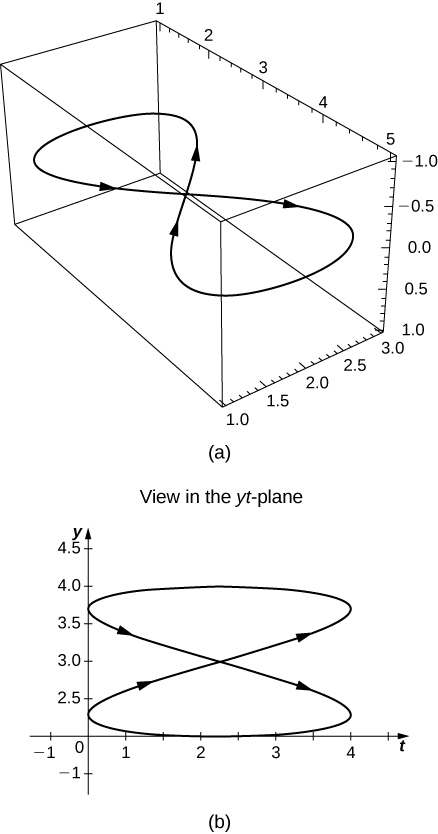
Trouver des équations dans\(x\) et\(y\) pour le chemin tracé par des fonctions à valeurs vectorielles
Pour les questions 26 à 33, éliminez le paramètre\(t\), écrivez l'équation en coordonnées cartésiennes, puis esquissez le graphique des fonctions à valeurs vectorielles.
26)\(\vecs r(t)=2t\hat{\mathbf{i}}+t^2 \hat{\mathbf{j}}\)
(Indice : Laissez\(x=2t\) et\(y=t^2\). Résolvez la première équation par\(t\) en termes de\(x\) et remplacez ce résultat dans la deuxième équation.)
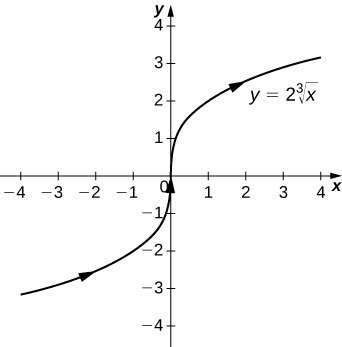
(27)\(\vecs r(t)=t^3 \hat{\mathbf{i}}+2t \hat{\mathbf{j}}\)
- Réponse
-
\(y=2\sqrt[3]{x}\), une variante de la fonction racine cubique
(28)\(\vecs r(t)=\sin t\,\hat{\mathbf{i}}+\cos t\,\hat{\mathbf{j}}\)
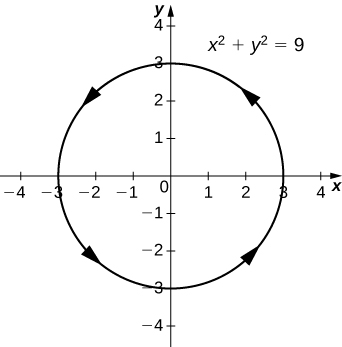
(29)\(\vecs r(t)=3\cos t\,\hat{\mathbf{i}}+3\sin t\,\hat{\mathbf{j}}\)
- Réponse
-
\(x^2+y^2=9\), un cercle centré\((0,0)\) avec un rayon 3 et une orientation dans le sens antihoraire
(30)\(\vecs r(t)=⟨ \sin t,4 \cos t⟩\)
31)\(\vecs r(t)=2\sin t\,\hat{\mathbf{i}}-3\cos t\,\hat{\mathbf{j}}\)
- Réponse
-
\(\frac{x^2}{4}+\frac{y^2}{9}=1\), une ellipse centrée sur,\((0,0)\) avec des points d'intersection à\(x = \pm2\) et\(y =\pm3\), et une orientation dans le sens des aiguilles d'une montre
32)\(\vecs r(t)=\tan t\,\hat{\mathbf{i}}-2\sec t\,\hat{\mathbf{j}}\)
33)\(\vecs r(t)=3\sec t\,\hat{\mathbf{i}}+4\tan t\,\hat{\mathbf{j}}\)
- Réponse
-
\(\frac{x^2}{9}-\frac{y^2}{16}=1\), une hyperbole centrée sur\((0,0)\) with\(x\) -intercepts\((3, 0)\) et\((-3, 0)\), avec l'orientation indiquée
Trouver une fonction à valeur vectorielle pour tracer le graphe d'une équation dans\(x\) et\(y\)
Pour les questions 34 à 40, trouvez une fonction à valeur vectorielle qui trace la courbe donnée dans la direction indiquée.
34)\(4x^2+9y^2=36\) ; dans le sens horaire et antihoraire
35)\(y=x^2\) ; de gauche à droite
- Réponse
- \(\vecs r(t)=⟨t,t^2⟩\), où\(t\) augmente
36) La ligne qui passe\(P\),\(Q\) où\(P\) est\((1,4,−2)\) et\(Q\) est\((3,9,6)\)
37) Le cercle\(x^2 + y^2 = 36\), orienté dans le sens des aiguilles d'une montre, avec position\((-6, 0)\) à la fois\(t = 0\).
- Réponse
- \(\vecs r(t)=-6\cos t\,\hat{\mathbf{i}}+6\sin t\,\hat{\mathbf{j}}\)
38) L'ellipse\(x^2 + \dfrac{y^2}{36} = 1\), orientée dans le sens antihoraire
- Réponse
- \(\vecs r(t)=\cos t\,\hat{\mathbf{i}}+6\sin t\,\hat{\mathbf{j}}\)
39) La partie supérieure de l'hyperbole est orientée de gauche à droite\(\dfrac{y^2}{36} - x^2 = 1\)
- Réponse
- \(\vecs r(t)=\tan t\,\hat{\mathbf{i}}+6\sec t\,\hat{\mathbf{j}}\)
40) L'hyperbole\(\dfrac{x^2}{49} - \dfrac{y^2}{64} = 1\), la pièce droite est orientée de bas en haut
- Réponse
- \(\vecs r(t)=7\sec t\,\hat{\mathbf{i}}+8\tan t\,\hat{\mathbf{j}}\)
Paramétrer un tracé par morceaux
Pour les questions 41 à 44, fournissez un paramétrage pour chaque chemin par morceaux. Essayez d'écrire un paramétrage qui commence par des valeurs de\(t = 0\) et progresse à mesure\(t\) que vous passez d'une pièce à l'autre.
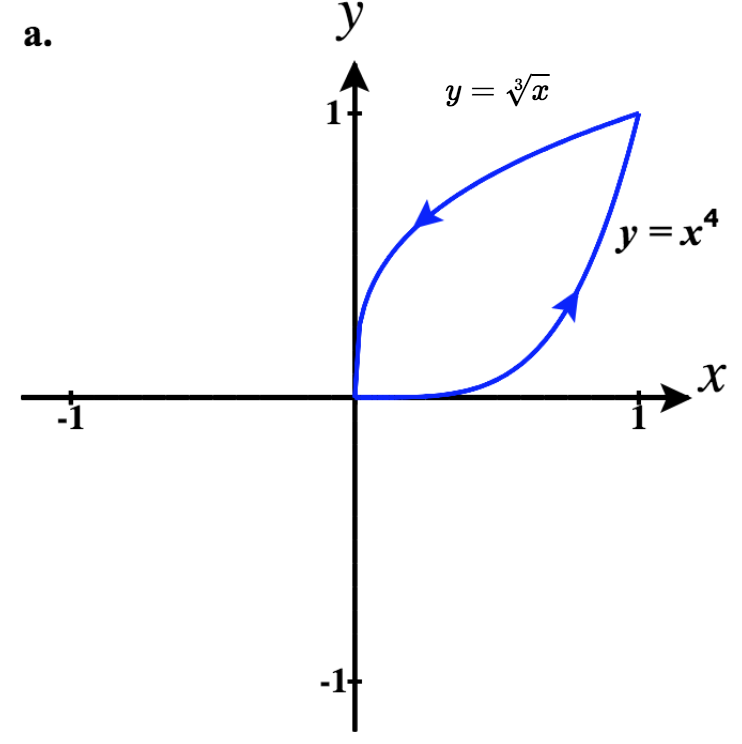
41)
- Réponse
- a.\(\vecs r_1(t)= t\,\hat{\mathbf{i}} + t^4 \,\hat{\mathbf{j}}\)\(0 \le t \le 1\)
\(\vecs r_2(t)= -t\,\hat{\mathbf{i}} + \sqrt[3]{-t} \,\hat{\mathbf{j}}\) pour\(-1 \le t \le 0\)
Donc, un paramétrage par morceaux de ce chemin est :
\ (\ vecs r (t) = \ begin {cases}
t \, \ hat {\ mathbf {i}} + t^4 \, \ hat {\ mathbf {j}}, & 0 \ le t \ le t \ le 1 \ \
\ left (2-t \ right) \, \ hat {\ mathbf {i}} + \ sqrt [3] {2-t} \, \ hat {\ mathbf {j}}, & 1 \ lt t
\ le 2 \ end {cases} \)
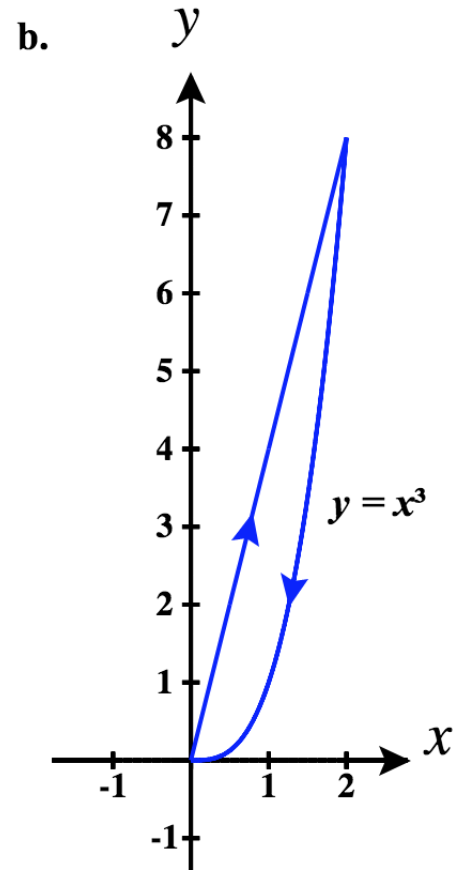
b.\(\vecs r_1(t)= t\,\hat{\mathbf{i}} + \sqrt[3]{t} \,\hat{\mathbf{j}}\)\(0 \le t \le 1\)
\(\vecs r_2(t)= -t\,\hat{\mathbf{i}} + (-t)^4 \,\hat{\mathbf{j}}\) pour\(-1 \le t \le 0\)
Donc, par morceaux le paramétrage de ce chemin est le suivant :
\ (\ vecs r (t) = \ begin {cases}
t \, \ hat {\ mathbf {i}} + \ sqrt [3] {t} \, \ hat {\ mathbf {j}}, & 0 \ le t \ le 1 \
\ \ left (2-t \ right) \, \ hat {\ mathbf {i}}} + left (2-t \ right) ^4 \, \ hat {\ mathbf {j}}, et 1 \ lt t \ le 2
\ end {cas} \)
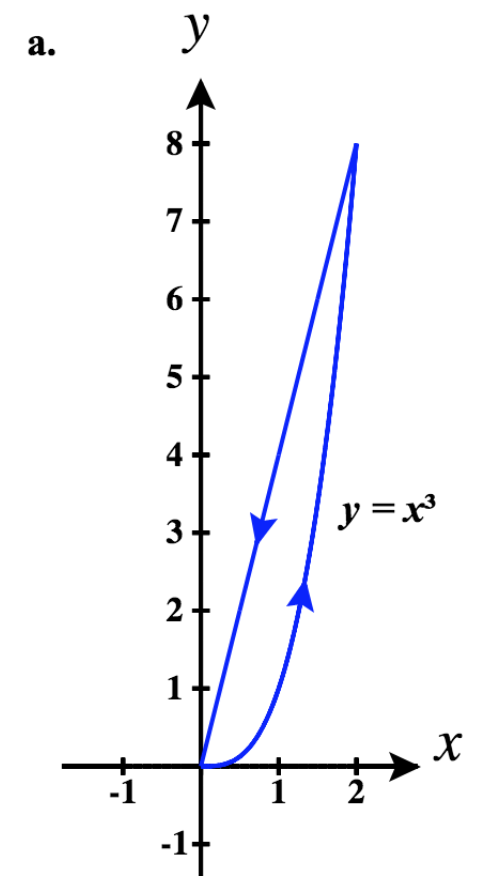
(42)
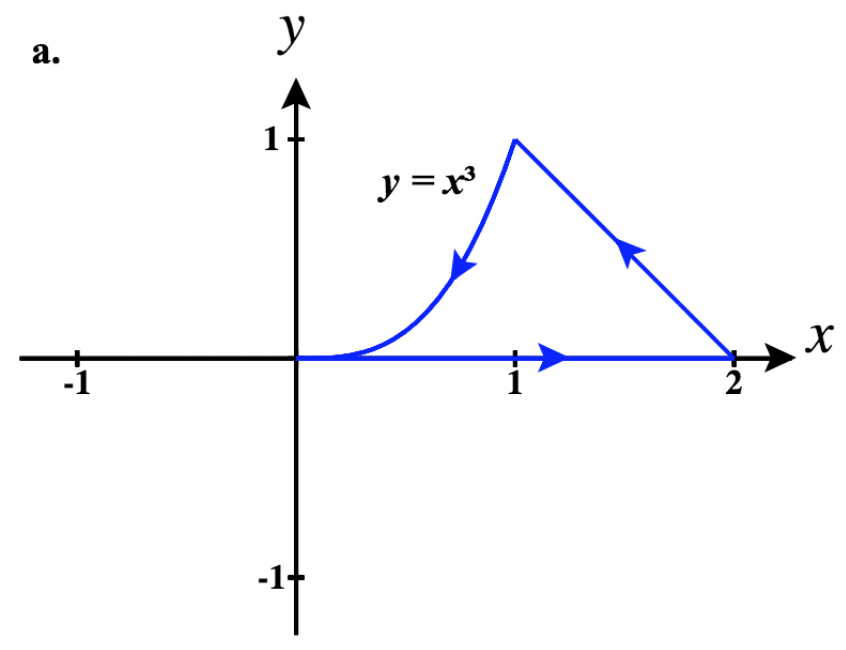
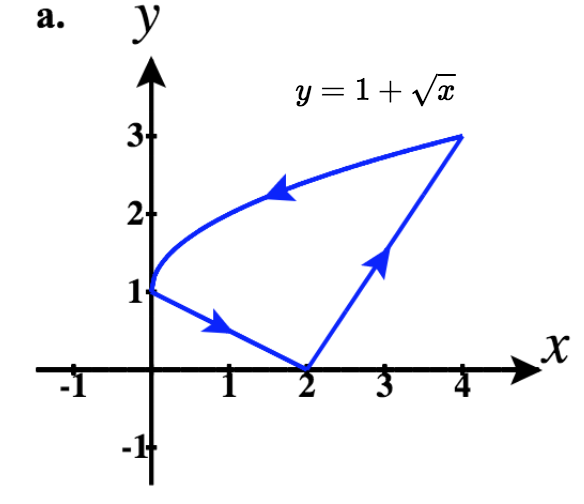
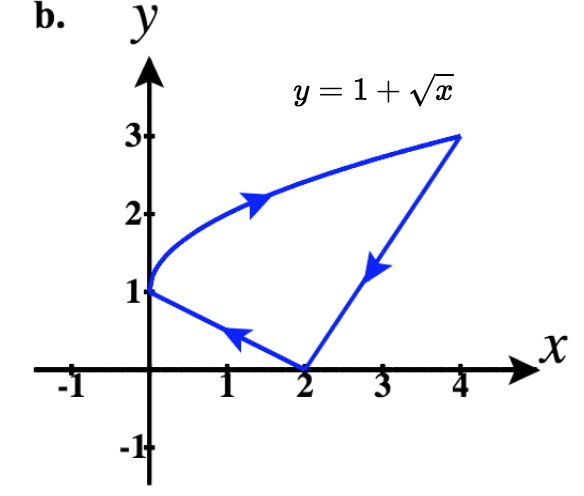
43)
- Réponse
- a.\(\vecs r_1(t)= t\,\hat{\mathbf{i}} +0 \,\hat{\mathbf{j}}\) pour for\(0 \le t \le 2\)
\(\vecs r_2(t)= -t\,\hat{\mathbf{i}} + \left(2 + t\right) \,\hat{\mathbf{j}}\)\(-2 \le t \le -1\)
\(\vecs r_3(t)= -t\,\hat{\mathbf{i}} + \left(-t\right)^3 \,\hat{\mathbf{j}}\) for\(-1 \le t \le 0\)
Donc, un paramétrage par morceaux de ce chemin est :
\ (\ vecs r (t) = \ begin {cases}
t \, \ hat {\ mathbf {i}}, & 0 \ le t \ le 2 \ \
\ left (4-t \ right) \, \ hat {\ mathbf {i}} + \ left (t-2 \ right) \, \ hat {\ mathbf {j}}, & 2 \ lt t \ le 3 \ \
\ left (4-t \ right) \, \ hat {\ mathbf {i}} + \ left (4-t \ right) ^3 \, \ hat {\ mathbf {j}}, & 3 \ lt t \ le 4
\ end {cas} \)
b.\(\vecs r_1(t)= t\,\hat{\mathbf{i}} + t^3 \,\hat{\mathbf{j}}\) pour for\(0 \le t \le 1\)
\(\vecs r_2(t)= t\,\hat{\mathbf{i}} + \left(2 - t\right) \,\hat{\mathbf{j}}\)\(1 \le t \le 2\)
\(\vecs r_3(t)= -t\,\hat{\mathbf{i}} + 0 \,\hat{\mathbf{j}}\) for\(-2 \le t \le 0\)
Donc, un paramétrage par morceaux de ce chemin est :
\ (\ vecs r (t) = \ begin {cases}
t \, \ hat {\ mathbf {i}} + t^3 \, \ hat {\ mathbf {j}}, & 0 \ le t \ le 1 \ \
t \, \ hat {\ mathbf {i}} + \ left (2 - t \ right) \, \ hat {\ mathbf {j}}, & 1 \ lt t \ le 2 \ \
\ left (4-t \ right) \, \ hat {\ mathbf {i}}, & 2 \ lt t \ le 4
\ end {cas} \)
44)
Questions supplémentaires sur les fonctions à valeur vectorielle
Pour les questions 45 à 48, considérez la courbe décrite par la fonction à valeur vectorielle\(\vecs r(t)=(50e^{−t}\cos t)\hat{\mathbf{i}}+(50e^{−t}\sin t)\hat{\mathbf{j}}+(5−5e^{−t})\hat{\mathbf{k}}\).
45) À quel point correspond le point initial du chemin\(\vecs r(0)\) ?
- Réponse
- \((50,0,0)\)
46) Qu'est-ce que c'est\(\lim \limits_{t \to \infty} \vecs r(t) \) ?
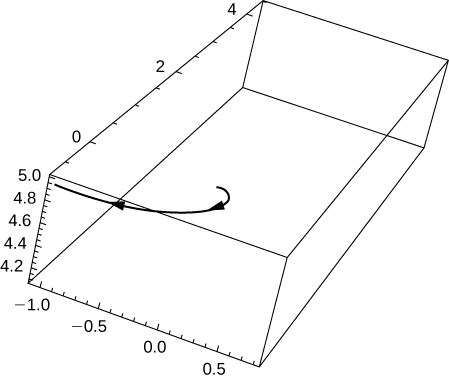
47) [T] Utilisez la technologie pour esquisser la courbe.
- Réponse
48) Éliminez le paramètre t pour indiquer\(z=5−\dfrac{r}{10}\) où\(r^2=x^2+y^2\).
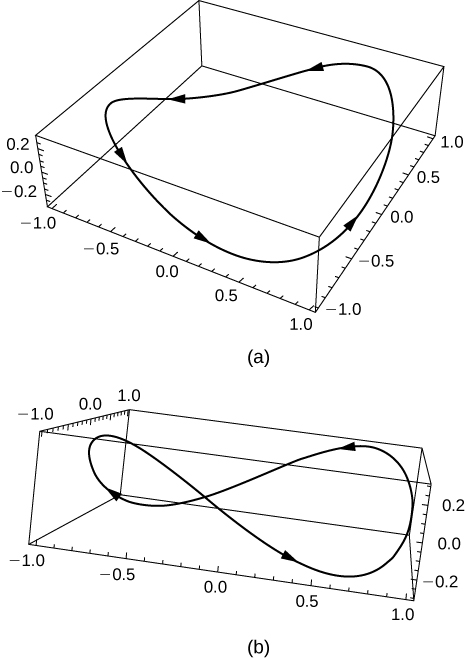
49) [T] Laisser\(\vecs r(t)=\cos t \hat{\mathbf{i}}+\sin t\hat{\mathbf{j}}+0.3 \sin (2t)\hat{\mathbf{k}}\). Utilisez la technologie pour représenter graphiquement la courbe (appelée courbe des montagnes russes) sur l'intervalle\([0,2\pi)\). Choisissez au moins deux vues pour déterminer les sommets et les vallées.
- Réponse
50) [T] Utilisez le résultat du problème précédent pour construire l'équation d'une montagne russe avec une forte pente depuis le sommet et une forte pente depuis la « vallée ». Ensuite, utilisez la technologie pour représenter graphiquement l'équation.
51) Utilisez les résultats des deux problèmes précédents pour construire l'équation de la trajectoire d'une montagne russe avec plus de deux points de retournement (sommets et vallées).
- Réponse
-
L'une des possibilités est\(\vecs r(t)=\cos t \hat{\mathbf{i}}+\sin t\hat{\mathbf{j}}+\sin (4t)\hat{\mathbf{k}}\). En augmentant le coefficient de\(t\) dans la troisième composante, le nombre de points de retournement augmentera.
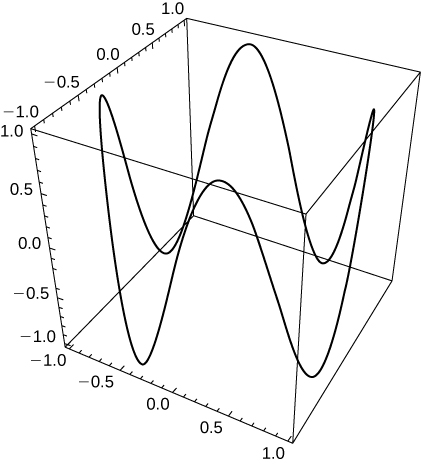
52) Terminez l'enquête suivante.
- Tracez la courbe\(\vecs r(t)=(4+\cos(18t))\cos(t)\hat{\mathbf{i}}+(4+\cos (18t)\sin (t))\hat{\mathbf{j}}+0.3 \sin(18t)\hat{\mathbf{k}}\) en utilisant les deux angles de vision de votre choix pour voir la forme générale de la courbe.
- La courbe ressemble-t-elle à un « slinky » ?
- Quelles modifications faut-il apporter à l'équation pour augmenter le nombre de bobines du slinky ?
Contributeurs
Paul Seeburger (Monroe Community College) a créé les problèmes 12, 14, 19, 22, 30-33, 37- 44.