13.1 : Fonctions à valeur vectorielle et courbes spatiales
- Page ID
- 197210
- Écrivez l'équation générale d'une fonction à valeur vectorielle sous forme de composante et sous forme de vecteur unitaire.
- Reconnaître les équations paramétriques d'une courbe spatiale.
- Décrivez la forme d'une hélice et écrivez son équation.
- Définissez la limite d'une fonction à valeur vectorielle.
Notre étude des fonctions à valeur vectorielle combine des idées issues de notre examen antérieur du calcul à variable unique avec notre description des vecteurs en trois dimensions tirée du chapitre précédent. Dans cette section, nous étendons les concepts des chapitres précédents et examinons également de nouvelles idées concernant les courbes dans l'espace tridimensionnel. Ces définitions et théorèmes appuient la présentation du matériel dans le reste de ce chapitre ainsi que dans les autres chapitres du texte.
Définition d'une fonction à valeur vectorielle
La première étape de l'étude du calcul des fonctions à valeur vectorielle consiste à définir ce qu'est exactement une fonction à valeur vectorielle. Nous pouvons ensuite examiner des graphes de fonctions à valeur vectorielle et voir comment elles définissent des courbes en deux et en trois dimensions.
Une fonction à valeur vectorielle est fonction de la forme
\[\vecs r(t)=f(t)\,\hat{\mathbf{i}}+g(t)\,\hat{\mathbf{j}} \; \; \text{or} \; \;\vecs r(t)=f(t)\,\hat{\mathbf{i}}+g(t)\,\hat{\mathbf{j}}+h(t)\,\hat{\mathbf{k}}, \nonumber \]
où les fonctions du composant\(f\)\(g\), et\(h\), sont des fonctions à valeur réelle du paramètre\(t\). Les fonctions à valeur vectorielle sont également écrites sous la forme
\[\vecs r(t)=⟨f(t),\,g(t)⟩ \; \; \text{or} \; \; \vecs r(t)=⟨f(t),\,g(t),\,h(t)⟩. \nonumber \]
Dans les deux cas, la première forme de la fonction définit une fonction bidimensionnelle à valeur vectorielle ; la seconde forme décrit une fonction tridimensionnelle à valeur vectorielle.
Le paramètre\(t\) peut se situer entre deux nombres réels :\(a≤t≤b\). Une autre possibilité est que la valeur de\(t\) pourrait prendre tous les nombres réels. Enfin, les fonctions du composant elles-mêmes peuvent avoir des restrictions de domaine qui imposent des restrictions sur la valeur de\(t\). Nous l'utilisons souvent\(t\) comme paramètre car cela\(t\) peut représenter le temps.
Pour chacune des fonctions à valeur vectorielle suivantes, évaluez\(\vecs r(0)\)\(\vecs r(\frac{\pi}{2})\), et\(\vecs r(\frac{2\pi}{3})\). Certaines de ces fonctions sont-elles soumises à des restrictions de domaine ?
- \(\vecs r(t)=4\cos t\,\hat{\mathbf{i}}+3\sin t\,\hat{\mathbf{j}}\)
- \(\vecs r(t)=3\tan t\,\hat{\mathbf{i}}+4 \sec t\,\hat{\mathbf{j}}+5t\,\hat{\mathbf{k}}\)
Solution
- Pour calculer chacune des valeurs de fonction, remplacez la valeur appropriée par\(t\) dans la fonction :
\ begin {align*} \ vecs r (0) \ ; = 4 \ cos (0) \ hat {\ mathbf {i}} +3 \ sin (0) \ hat {\ mathbf {j}} \ \ [4pt] =4 \ hat {\ mathbf {i}} +0 \ hat {\ mathbf {j}} =4 \ hat {\ mathbf {i}} \ \ [4pt] \ vecs r \ left (\ frac {\ pi} {2} \ right) \ ; = 4 \ cos \ left (\ frac {π} {2} \ right) \ hat {\ mathbf {i}} +3 \ sin \ left (\ frac {π} {2} \ right) \ hat {\ mathbf {j}} \ \ [4pt] = 0 \ hat {\ mathbf {i}} + 3 \ hat {\ mathbf {j}} =3 \ hat {\ mathbf {j}} \ \ [4pt] \ vecs r \ left (\ frac {2 \ pi} {3} \ right) \ ; =4 \ cos \ left (\ frac {2π} {3} \ right) \ hat {\ mathbf {i}} +3 \ sin \ left (\ frac {2π} {3} \ droite) \ hat {\ mathbf {j}} \ \ [4pt] =4 \ left (− \ tfrac {1} {2} \ right) \ hat {\ mathbf {i}} +3 \ left (\ tfrac {\ sqrt {3}}} {2} \ right) \ hat {\ mathbf {j}} =−2 \ hat {\ mathbf {i}} + \ frac {3 \ sqrt {3}} {2} \ hat {\ mathbf {j}} \ end {align*}
Pour déterminer si cette fonction est soumise à des restrictions de domaine, considérez les fonctions du composant séparément. La première fonction constitutive est\(f(t)=4 \cos t\) et la seconde fonction constitutive l'est\(g(t)=3\sin t\). Aucune de ces fonctions n'a de restriction de domaine, de sorte que le domaine de\(\vecs r(t)=4\cos t\,\hat{\mathbf{i}}+3 \sin t \,\hat{\mathbf{j}}\) est composé uniquement de nombres réels. - Pour calculer chacune des valeurs de fonction, remplacez la valeur appropriée de t dans la fonction :\[\begin{align*}\vecs r(0) \; = 3\tan(0)\hat{\mathbf{i}}+4\sec(0) \hat{\mathbf{j}}+5(0) \hat{\mathbf{k}} \\[4pt] = 0\hat{\mathbf{i}}+4j+0 \hat{\mathbf{k}}=4 \hat{\mathbf{j}} \\[4pt] \vecs r\left(\frac{\pi}{2}\right) \; = 3\tan\left(\frac{\pi}{2}\right)\hat{\mathbf{i}}+4\sec\left(\frac{\pi}{2}\right) \hat{\mathbf{j}}+5\left(\frac{\pi}{2}\right) \hat{\mathbf{k}},\,\text{which does not exist} \\[4pt] \vecs r\left(\frac{2\pi}{3}\right) \; =3\tan\left(\frac{2 \pi}{3}\right)\hat{\mathbf{i}}+4\sec\left(\frac{2\pi}{3}\right) \hat{\mathbf{j}}+5\left(\frac{2\pi}{ 3}\right) \hat{\mathbf{k}} \\[4pt] =3(−\sqrt{3})\hat{\mathbf{i}}+4(−2)\hat{\mathbf{j}}+\frac{10π}{3} \hat{\mathbf{k}} \\[4pt] =(-3\sqrt{3})\hat{\mathbf{i}}−8\hat{\mathbf{j}}+\frac{10π}{3} \hat{\mathbf{k}}\end{align*}\] Pour déterminer si cette fonction comporte des restrictions de domaine, considérez les fonctions des composants séparément. La première fonction constitutive est\(f(t)=3\tan t\), la deuxième fonction constitutive l'est\(g(t)=4\sec t\) et la troisième fonction constitutive l'est\(h(t)=5t\). Les deux premières fonctions ne sont pas définies pour des multiples impairs de\(\frac{\pi}{2}\), de sorte que la fonction n'est pas définie pour des multiples impairs de\(\frac{\pi}{2}\). Par conséquent,\[\text{D}_{\vecs r}=\Big\{t\,|\,t≠ \frac{(2n+1)\pi}{2}\Big\},\nonumber \] où\(n\) est n'importe quel entier.
Pour la fonction à valeur vectorielle\(\vecs r(t)=(t^2−3t) \,\hat{\mathbf{i}}+(4t+1) \,\hat{\mathbf{j}}\)\(\vecs r(0),\, \vecs r(1)\), évaluez et\(\vecs r(−4)\). Cette fonction comporte-t-elle des restrictions de domaine ?
- Allusion
-
Remplacez les valeurs appropriées par\(t\) dans la fonction.
- Réponse
-
\(\vecs r(0) = \hat{\mathbf{j}},\, \vecs r(1)=−2 \hat{\mathbf{i}}+5 \hat{\mathbf{j}},\, \vecs r(−4)=28 \hat{\mathbf{i}}−15 \hat{\mathbf{j}}\)
Le domaine de\(\vecs r(t)=(t^2−3t)\hat{\mathbf{i}}+(4t+1)\hat{\mathbf{j}}\) ce sont tous des nombres réels.
L'exemple\(\PageIndex{1}\) illustre un concept important. Le domaine d'une fonction à valeur vectorielle est constitué de nombres réels. Le domaine peut être composé uniquement de nombres réels ou d'un sous-ensemble de nombres réels. La plage d'une fonction à valeur vectorielle est constituée de vecteurs. Chaque nombre réel dans le domaine d'une fonction à valeur vectorielle est mappé sur un vecteur bidimensionnel ou tridimensionnel.
Représentation graphique de fonctions à valeur vectorielle
Rappelons qu'un vecteur plan est composé de deux quantités : direction et magnitude. Étant donné n'importe quel point du plan (le point initial), si nous nous déplaçons dans une direction spécifique sur une distance spécifique, nous arrivons à un deuxième point. Cela représente le point terminal du vecteur. Nous calculons les composantes du vecteur en soustrayant les coordonnées du point initial des coordonnées du point terminal.
Un vecteur est considéré comme étant en position standard si le point initial est situé à l'origine. Lors de la représentation graphique d'une fonction à valeur vectorielle, nous représentons généralement les vecteurs du domaine de la fonction en position standard, car cela garantit l'unicité du graphe. Cette convention s'applique également aux graphes de fonctions tridimensionnelles à valeur vectorielle. Le graphe d'une fonction à valeur vectorielle du formulaire
\[\vecs r(t)=f(t)\, \hat{\mathbf{i}}+g(t)\,\hat{\mathbf{j}} \nonumber \]
se compose de l'ensemble de tous les points\((f(t),\,g(t))\), et la trajectoire qu'il trace est appelée courbe plane. Le graphe d'une fonction à valeur vectorielle du formulaire
\[\vecs r(t)=f(t) \,\hat{\mathbf{i}}+g(t) \,\hat{\mathbf{j}}+h(t) \,\hat{\mathbf{k}} \nonumber \]
se compose de l'ensemble de tous les points\((f(t),\,g(t),\,h(t))\), et la trajectoire qu'il trace est appelée courbe spatiale. Toute représentation d'une courbe plane ou d'une courbe spatiale à l'aide d'une fonction à valeur vectorielle est appelée paramétrage vectoriel de la courbe.
Chaque courbe plane et courbe spatiale possède une orientation, indiquée par des flèches tracées sur la courbe, qui indique la direction du mouvement le long de la courbe lorsque la valeur du paramètre\(t\) augmente.
Créez un graphique de chacune des fonctions à valeurs vectorielles suivantes :
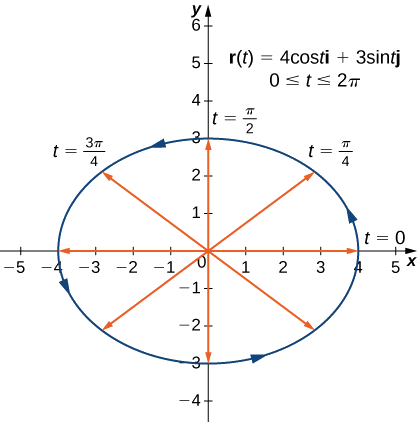
- La courbe plane représentée par\(\vecs r(t)=4 \cos t \,\hat{\mathbf{i}}+3 \sin t \,\hat{\mathbf{j}}\),\(0≤t≤2\pi\)
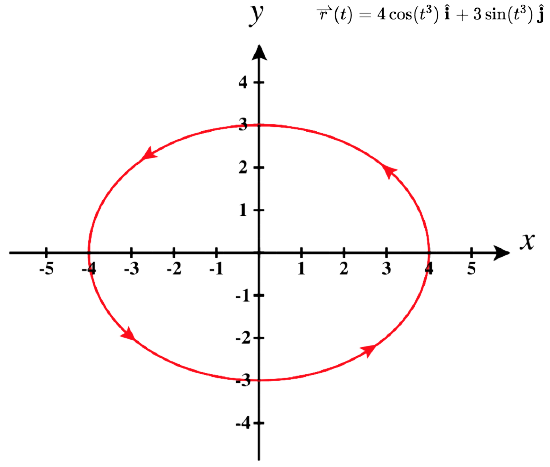
- La courbe plane représentée par\(\vecs r(t)=4 \cos(t^3) \,\hat{\mathbf{i}}+3 \sin(t^3) \,\hat{\mathbf{j}}\),\(0≤t≤\sqrt[3]{2\pi}\)
- La courbe spatiale représentée par\(\vecs r(t)=4 \cos t \,\hat{\mathbf{i}}+4 \sin t \,\hat{\mathbf{j}}+t \,\hat{\mathbf{k}}\),\(0≤t≤4\pi\)
Solution
1. Comme pour tout graphique, nous commençons par un tableau de valeurs. Nous tracons ensuite chacun des vecteurs de la deuxième colonne du tableau en position standard et connectons les points terminaux de chaque vecteur pour former une courbe (Figure\(\PageIndex{1}\)). Cette courbe s'avère être une ellipse centrée à l'origine.
| \(t\) | \(\vecs r(t)\) | \(t\) | \(\vecs r(t)\) |
|---|---|---|---|
| \ (t \) » style="vertical-align:middle ; « >\(0\) | \ (\ vecs r (t) \) » style="vertical-align:middle ; « >\(4\hat{\mathbf{i}}\) | \ (t \) » style="vertical-align:middle ; « >\(\pi\) | \ (\ vecs r (t) \) » style="vertical-align:middle ; « >\(-4\hat{\mathbf{i}}\) |
| \ (t \) » style="vertical-align:middle ; « >\(\dfrac{\pi}{4}\) | \ (\ vecs r (t) \) » style="vertical-align:middle ; « >\(2 \sqrt{2} \hat{\mathbf{i}} + \frac{3 \sqrt{2}}{2}\hat{\mathbf{j}}\) | \ (t \) » style="vertical-align:middle ; « >\(\dfrac{5\pi}{4}\) | \ (\ vecs r (t) \) » style="vertical-align:middle ; « >\(-2 \sqrt{2} \hat{\mathbf{i}} - \frac{3 \sqrt{2}}{2}\hat{\mathbf{j}}\) |
| \ (t \) » style="vertical-align:middle ; « >\(\dfrac{\pi}{2}\) | \ (\ vecs r (t) \) » style="vertical-align:middle ; « >\(\mathrm{3\hat{\mathbf{j}}}\) | \ (t \) » style="vertical-align:middle ; « >\(\dfrac{3\pi}{2}\) | \ (\ vecs r (t) \) » style="vertical-align:middle ; « >\(\mathrm{-3\hat{\mathbf{j}}}\) |
| \ (t \) » style="vertical-align:middle ; « >\(\dfrac{3\pi}{4}\) | \ (\ vecs r (t) \) » style="vertical-align:middle ; « >\( -2 \sqrt{2} \hat{\mathbf{i}} + \frac{3 \sqrt{2}}{2}\hat{\mathbf{j}}\) | \ (t \) » style="vertical-align:middle ; « >\(\dfrac{7\pi}{4}\) | \ (\ vecs r (t) \) » style="vertical-align:middle ; « >\( 2 \sqrt{2} \hat{\mathbf{i}} - \frac{3 \sqrt{2}}{2}\hat{\mathbf{j}}\) |
| \ (t \) » style="vertical-align:middle ; « >\(2\pi\) | \ (\ vecs r (t) \) » style="vertical-align:middle ; « >\(4\hat{\mathbf{i}}\) | \ (t \) » style="vertical-align:middle ; « > | \ (\ vecs r (t) \) » style="vertical-align:middle ; « > |
2. Le tableau des valeurs pour\(\vecs r(t)=4 \cos(t^3) \,\hat{\mathbf{i}}+3 \sin(t^3) \,\hat{\mathbf{j}}\),\(0≤t≤\sqrt[3]{2\pi}\) est le suivant :
| \(t\) | \(\vecs r(t)\) | \(t\) | \(\vecs r(t)\) |
|---|---|---|---|
| \ (t \) » style="vertical-align:middle ; « >\(0\) | \ (\ vecs r (t) \) » style="vertical-align:middle ; « >\(\mathrm{4\hat{\mathbf{i}}}\) | \ (t \) » style="vertical-align:middle ; « >\(\displaystyle\sqrt[3]{\pi}\) | \ (\ vecs r (t) \) » style="vertical-align:middle ; « >\(\mathrm{-4\hat{\mathbf{i}}}\) |
| \ (t \) » style="vertical-align:middle ; « >\(\displaystyle \sqrt[3]{\dfrac{\pi}{4}}\) | \ (\ vecs r (t) \) » style="vertical-align:middle ; « >\(\mathrm{ 2 \sqrt{2} \hat{\mathbf{i}} + \frac{3 \sqrt{2}}{2}\hat{\mathbf{j}}}\) | \ (t \) » style="vertical-align:middle ; « >\(\displaystyle \sqrt[3]{\dfrac{5\pi}{4}}\) | \ (\ vecs r (t) \) » style="vertical-align:middle ; « >\(\mathrm{ -2 \sqrt{2} \hat{\mathbf{i}} - \frac{3 \sqrt{2}}{2}\hat{\mathbf{j}}}\) |
| \ (t \) » style="vertical-align:middle ; « >\(\displaystyle \sqrt[3]{\dfrac{\pi}{2}}\) | \ (\ vecs r (t) \) » style="vertical-align:middle ; « >\(\mathrm{3\hat{\mathbf{j}}}\) | \ (t \) » style="vertical-align:middle ; « >\(\displaystyle \sqrt[3]{\dfrac{3\pi}{2}}\) | \ (\ vecs r (t) \) » style="vertical-align:middle ; « >\(\mathrm{-3\hat{\mathbf{j}}}\) |
| \ (t \) » style="vertical-align:middle ; « >\(\displaystyle \sqrt[3]{\dfrac{3\pi}{4}}\) | \ (\ vecs r (t) \) » style="vertical-align:middle ; « >\(\mathrm{ -2 \sqrt{2} \hat{\mathbf{i}} + \frac{3 \sqrt{2}}{2}\hat{\mathbf{j}}}\) | \ (t \) » style="vertical-align:middle ; « >\(\displaystyle \sqrt[3]{\dfrac{7\pi}{4}}\) | \ (\ vecs r (t) \) » style="vertical-align:middle ; « >\(\mathrm{ 2 \sqrt{2} \hat{\mathbf{i}} - \frac{3 \sqrt{2}}{2}\hat{\mathbf{j}}}\) |
| \ (t \) » style="vertical-align:middle ; « >\( \displaystyle\sqrt[3]{2\pi}\) | \ (\ vecs r (t) \) » style="vertical-align:middle ; « >\(\mathrm{4\hat{\mathbf{i}}}\) | \ (t \) » style="vertical-align:middle ; « > | \ (\ vecs r (t) \) » style="vertical-align:middle ; « > |
Le graphique de cette courbe est également une ellipse centrée à l'origine.
3. Nous suivons la même procédure pour une fonction vectorielle tridimensionnelle.
| \(t\) | \(\vecs r(t)\) | \(t\) | \(\vecs r(t)\) |
|---|---|---|---|
| \ (t \) » style="vertical-align:middle ; « >\(\mathrm{0}\) | \ (\ vecs r (t) \) » style="vertical-align:middle ; « >\(\mathrm{4\hat{\mathbf{i}}}\) | \ (t \) » style="vertical-align:middle ; « >\(\mathrm{\pi}\) | \ (\ vecs r (t) \) » style="vertical-align:middle ; « >\(\mathrm{-4\hat{\mathbf{i}}}+ \pi \hat{\mathbf{k}}\) |
| \ (t \) » style="vertical-align:middle ; « >\(\dfrac{\pi}{4}\) | \ (\ vecs r (t) \) » style="vertical-align:middle ; « >\(\mathrm{2 \sqrt{2} \hat{\mathbf{i}} + 2\sqrt{2} \hat{\mathbf{j}} + \frac{\pi}{4} \hat{\mathbf{k}}}\) | \ (t \) » style="vertical-align:middle ; « >\(\dfrac{5\pi}{4}\) | \ (\ vecs r (t) \) » style="vertical-align:middle ; « >\(\mathrm{ -2 \sqrt{2} \hat{\mathbf{i}} - 2\sqrt{2} \hat{\mathbf{j}} + \frac{5\pi}{4} \hat{\mathbf{k}}}\) |
| \ (t \) » style="vertical-align:middle ; « >\(\dfrac{\pi}{2}\) | \ (\ vecs r (t) \) » style="vertical-align:middle ; « >\(\mathrm{4\hat{\mathbf{j}} +\frac{\pi}{2} \hat{\mathbf{k}}}\) | \ (t \) » style="vertical-align:middle ; « >\(\dfrac{3\pi}{2}\) | \ (\ vecs r (t) \) » style="vertical-align:middle ; « >\(\mathrm{-4\hat{\mathbf{j}} +\frac{3\pi}{2} \hat{\mathbf{k}}}\) |
| \ (t \) » style="vertical-align:middle ; « >\(\dfrac{3\pi}{4}\) | \ (\ vecs r (t) \) » style="vertical-align:middle ; « >\(\mathrm{ -2 \sqrt{2} \hat{\mathbf{i}} + 2\sqrt{2} \hat{\mathbf{j}} + \frac{3\pi}{4} \hat{\mathbf{k}}}\) | \ (t \) » style="vertical-align:middle ; « >\(\dfrac{7\pi}{4}\) | \ (\ vecs r (t) \) » style="vertical-align:middle ; « >\(\mathrm{ 2 \sqrt{2} \hat{\mathbf{i}} - 2\sqrt{2} \hat{\mathbf{j}} + \frac{7\pi}{4} \hat{\mathbf{k}}}\) |
| \ (t \) » style="vertical-align:middle ; « >\(\mathrm{2\pi}\) | \ (\ vecs r (t) \) » style="vertical-align:middle ; « >\(\mathrm{4\hat{\mathbf{j}} + 2\pi \hat{\mathbf{k}}}\) | \ (t \) » style="vertical-align:middle ; « > | \ (\ vecs r (t) \) » style="vertical-align:middle ; « > |
Les valeurs se répètent alors, à l'exception du fait que le coefficient de\(\hat{\mathbf{k}}\) augmente toujours (\(\PageIndex{3}\)). Cette courbe s'appelle une hélice. Notez que si le\(\hat{\mathbf{k}}\) composant est éliminé, la fonction devient\(\vecs r(t)=4\cos t \hat{\mathbf{i}}+ 4\sin t \hat{\mathbf{j}}\), c'est-à-dire un cercle de rayon 4 centré sur l'origine.

Vous remarquerez peut-être que les graphiques des parties a. et b. sont identiques. Cela se produit parce que la fonction décrivant la courbe b est une soi-disant reparamétrisation de la fonction décrivant la courbe a. En fait, toute courbe possède un nombre infini de reparamétrisations ; par exemple, nous pouvons la\(t\) remplacer par\(2t\) dans n'importe laquelle des trois courbes précédentes sans changer la forme de la courbe. L'intervalle sur lequel\(t\) est défini peut changer, mais c'est tout. Nous reviendrons sur cette idée plus loin dans ce chapitre lorsque nous étudierons la paramétrisation de la longueur des arcs. Comme indiqué, le nom de la forme de la courbe du graphe en\(\PageIndex{3}\) est une hélice. La courbe ressemble à un ressort, avec une section circulaire orientée vers le bas le long de\(z\) l'axe. Il est également possible qu'une hélice soit elliptique en section transversale. Par exemple, la fonction à valeur vectorielle\(\vecs r(t)=4 \cos t \,\hat{\mathbf{i}}+3 \sin t \,\hat{\mathbf{j}}+t \,\hat{\mathbf{k}}\) décrit une hélice elliptique. La projection de cette hélice dans le\(xy\) plan est une ellipse. Enfin, les flèches du graphe de cette hélice indiquent l'orientation de la courbe au fur et à mesure qu'\(t\)elle progresse de\(0\) à\(4π\).
Créez un graphique de la fonction à valeur vectorielle\(\vecs r(t)=(t^2−1)\hat{\mathbf{i}}+(2t−3) \hat{\mathbf{j}}\),\(0≤t≤3\).
- Allusion
-
Commencez par créer un tableau de valeurs, puis tracez les vecteurs pour chaque valeur de\(t\).
- Réponse
-
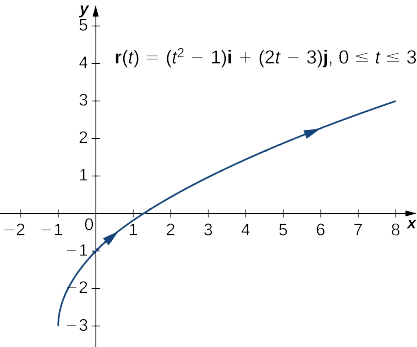
À ce stade, vous remarquerez peut-être une similitude entre les fonctions à valeur vectorielle et les courbes paramétrées. En effet, étant donné une fonction à valeur vectorielle,\(\vecs r(t)=f(t)\,\hat{\mathbf{i}}+g(t)\,\hat{\mathbf{j}}\) nous pouvons définir\(x=f(t)\) et\(y=g(t)\). S'il existe une restriction sur les valeurs de\(t\) (par exemple,\(t\) est limitée à l'intervalle\([a,b]\) pour certaines constantes)\(a<b\), cette restriction est appliquée au paramètre. Le graphe de la fonction paramétrée serait alors conforme au graphe de la fonction à valeur vectorielle, sauf que le graphe à valeur vectorielle représenterait des vecteurs plutôt que des points. Comme nous pouvons paramétrer une courbe définie par une fonction\(y=f(x)\), il est également possible de représenter une courbe plane arbitraire par une fonction à valeur vectorielle.
Limites et continuité d'une fonction à valeur vectorielle
Nous examinons maintenant la limite d'une fonction à valeur vectorielle. Il est important de comprendre cela pour étudier le calcul des fonctions à valeur vectorielle.
Une fonction à valeur vectorielle\(\vecs r\) s'approche de la limite au\(\vecs L\) fur et à mesure qu'elle\(t\)\(a\) s'approche
\[\lim \limits_{t \to a} \vecs r(t) = \vecs L, \nonumber \]
fourni
\[\lim \limits_{t \to a} \big\| \vecs r(t) - \vecs L \big\| = 0. \nonumber \]
Il s'agit d'une définition rigoureuse de la limite d'une fonction à valeur vectorielle. En pratique, nous utilisons le théorème suivant :
Laissez\(f\)\(g\), et\(h\) soyez des fonctions de\(t\). Ensuite, la limite de la fonction à valeur vectorielle à\(\vecs r(t)=f(t) \hat{\mathbf{i}}+g(t) \hat{\mathbf{j}}\) mesure que t s'approche de a est donnée par
\[\lim \limits_{t \to a} \vecs r(t) = [\lim \limits_{t \to a} f(t)] \hat{\mathbf{i}} + [\lim \limits_{t \to a} g(t)] \hat{\mathbf{j}} , \label{Th1} \]
sous réserve des limites\(\lim \limits_{t \to a} f(t)\) et de l'\(\lim \limits_{t \to a} g(t)\)existence.
De même, la limite de la fonction à valeur vectorielle à\(\vecs r(t)=f(t) \hat{\mathbf{i}}+g(t) \hat{\mathbf{j}}+h(t) \hat{\mathbf{k}}\) mesure que l'on\(a\) s'\(t\)approche est donnée par
\[\lim \limits_{t \to a} \vecs r(t) = [\lim \limits_{t \to a} f(t)] \hat{\mathbf{i}} + [\lim \limits_{t \to a} g(t)] \hat{\mathbf{j}} +[\lim \limits_{t \to a} h(t)] \hat{\mathbf{k}} , \label{Th2} \]
sous réserve des limites\(\lim \limits_{t \to a} f(t)\),\(\lim \limits_{t \to a} g(t)\) et\(\lim \limits_{t \to a} h(t)\) existent.
Dans l'exemple suivant, nous montrons comment calculer la limite d'une fonction à valeur vectorielle.
Pour chacune des fonctions à valeurs vectorielles suivantes, calculez\(\lim \limits_{t \to 3}\vecs r(t)\) pour
- \(\vecs r(t)=(t^2−3t+4) \hat{\mathbf{i}}+(4t+3)\hat{\mathbf{j}}\)
- \(\vecs r(t)=\frac{2t−4}{t+1}\hat{\mathbf{i}}+\frac{t}{t^2+1} \hat{\mathbf{j}}+(4t−3) \hat{\mathbf{k}}\)
Solution
- Utilisez l'équation \ ref {Th1} et remplacez la valeur\(t=3\) dans les deux expressions du composant :
\[ \begin{align*} \lim \limits_{t \to 3} \vecs r(t) \; = \lim \limits_{t \to 3} \left[(t^2−3t+4) \hat{\mathbf{i}} + (4t+3) \hat{\mathbf{j}}\right] \\[4pt] = \left[\lim \limits_{t \to 3} (t^2−3t+4)\right]\hat{\mathbf{i}}+\left[\lim \limits_{t \to 3} (4t+3)\right] \hat{\mathbf{j}} \\[4pt] = 4 \hat{\mathbf{i}}+15 \hat{\mathbf{j}} \end{align*}\]
- Utilisez l'équation \ ref {Th2} et remplacez la valeur\(t=3\) dans les trois expressions constitutives :
\[ \begin{align*} \lim \limits_{t \to 3} \vecs r(t) \; = \lim \limits_{t \to 3}\left(\dfrac{2t−4}{t+1}\hat{\mathbf{i}}+\dfrac{t}{t^2+1}\hat{\mathbf{j}}+(4t−3) \hat{\mathbf{k}}\right) \\[4pt] = \left[\lim \limits_{t \to 3} \left(\dfrac{2t−4}{t+1}\right)\right]\hat{\mathbf{i}}+\left[\lim \limits_{t \to 3} \left(\dfrac{t}{t^2+1}\right)\right] \hat{\mathbf{j}} +\left[\lim \limits_{t \to 3} (4t−3)\right] \hat{\mathbf{k}} \\[4pt] = \tfrac{1}{2} \hat{\mathbf{i}}+\tfrac{3}{10}\hat{\mathbf{j}}+9 \hat{\mathbf{k}} \end{align*}\]
Calculer\(\lim \limits_{t \to 2} \vecs r(t)\) pour la fonction\(\vecs r(t) = \sqrt{t^2 + 3t - 1}\,\hat{\mathbf{i}}−(4t-3)\hat{\mathbf{j}}− \sin \frac{(t+1)\pi}{2}\hat{\mathbf{k}}\)
- Allusion
-
Utilisez l'équation \ ref {Th2} du théorème précédent.
- Réponse
-
\[\lim \limits_{t \to 2} \vecs r(t) = 3\hat{\mathbf{i}}−5\hat{\mathbf{j}}+\hat{\mathbf{k}} \nonumber \]
Maintenant que nous savons comment calculer la limite d'une fonction à valeur vectorielle, nous pouvons définir la continuité en un point pour une telle fonction.
Laissez\(f\)\(g\), et\(h\) soyez des fonctions de\(t\). Ensuite, la fonction à valeur vectorielle\(\vecs r(t)=f(t) \hat{\mathbf{i}}+g(t)\hat{\mathbf{j}}\) est continue au point\(t=a\) si les trois conditions suivantes sont réunies :
- \(\vecs r(a)\)existe
- \(\lim \limits_{t \to a} \vecs r(t)\)existe
- \(\lim \limits_{t \to a} \vecs r(t) = \vecs r(a)\)
De même, la fonction à valeur vectorielle\(\vecs r(t)=f(t) \hat{\mathbf{i}}+g(t)\hat{\mathbf{j}}+h(t)\hat{\mathbf{k}}\) est continue au point\(t=a\) si les trois conditions suivantes sont réunies :
- \(\vecs r(a)\)existe
- \(\lim \limits_{t \to a} \vecs r(t)\)existe
- \(\lim \limits_{t \to a} \vecs r(t) = \vecs r(a)\)
Résumé
- Une fonction à valeur vectorielle est fonction de la forme\(\vecs r(t)=f(t) \hat{\mathbf{i}}+ g(t) \hat{\mathbf{j}}\) ou\(\vecs r(t)=f(t) \hat{\mathbf{i}}+g(t) \hat{\mathbf{j}}+h(t) \hat{\mathbf{k}}\), lorsque le composant fonctionne\(f\)\(g\), et\(h\) sont des fonctions à valeur réelle du paramètre\(t\).
- Le graphe d'une fonction de la forme à valeur vectorielle\(\vecs r(t)=f(t) \hat{\mathbf{i}}+g(t) \hat{\mathbf{j}}\) est appelé courbe plane. Le graphe d'une fonction de la forme à valeur vectorielle\(\vecs r(t)=f(t)\hat{\mathbf{i}}+g(t)\hat{\mathbf{j}}+h(t) \hat{\mathbf{k}}\) est appelé courbe spatiale.
- Il est possible de représenter une courbe plane arbitraire par une fonction à valeur vectorielle.
- Pour calculer la limite d'une fonction à valeur vectorielle, calculez les limites des fonctions composantes séparément.
Équations clés
- Fonction à valeur vectorielle
\(\vecs r(t)=f(t) \hat{\mathbf{i}}+g(t) \hat{\mathbf{j}}\) ou\(\vecs r(t)=f(t) \hat{\mathbf{i}}+g(t) \hat{\mathbf{j}}+h(t) \hat{\mathbf{k}}\), ou\(\vecs r(t)=⟨f(t),g(t)⟩\) ou\(\vecs r(t)=⟨f(t),g(t),h(t)⟩\) - Limite d'une fonction à valeur vectorielle
\(\lim \limits_{t \to a} \vecs r(t) = [\lim \limits_{t \to a} f(t)] \hat{\mathbf{i}} + [\lim \limits_{t \to a} g(t)] \hat{\mathbf{j}}\) ou\(\lim \limits_{t \to a} \vecs r(t) = [\lim \limits_{t \to a} f(t)] \hat{\mathbf{i}} + [\lim \limits_{t \to a} g(t)] \hat{\mathbf{j}} + [\lim \limits_{t \to a} h(t)] \hat{\mathbf{k}}\)
Lexique
- fonctions des composants
- les fonctions composantes de la fonction à valeur vectorielle\(\vecs r(t)=f(t)\hat{\mathbf{i}}+g(t)\hat{\mathbf{j}}\) sont\(f(t)\) et\(g(t)\), et les fonctions composantes de la fonction à valeur vectorielle\(\vecs r(t)=f(t)\hat{\mathbf{i}}+g(t)\hat{\mathbf{j}}+h(t)\hat{\mathbf{k}}\) sont\(f(t)\),\(g(t)\) et\(h(t)\)
- hélice
- une courbe tridimensionnelle en forme de spirale
- limite d'une fonction à valeur vectorielle
- une fonction à valeur vectorielle\(\vecs r(t)\) a une limite à\(\vecs L\) mesure que l'\(a\)on s'\(t\)approche si\(\lim \limits{t \to a} \left| \vecs r(t) - \vecs L \right| = 0\)
- courbe plane
- l'ensemble des paires ordonnées\((f(t),g(t))\) ainsi que leurs équations paramétriques de définition\(x=f(t)\) et\(y=g(t)\)
- reparamétrage
- un paramétrage alternatif d'une fonction à valeur vectorielle donnée
- courbe spatiale
- l'ensemble des triples\((f(t),g(t),h(t))\) ordonnés avec leurs équations paramétriques de définition\(x=f(t)\),\(y=g(t)\) et\(z=h(t)\)
- paramétrage vectoriel
- toute représentation d'un plan ou d'une courbe spatiale à l'aide d'une fonction à valeur vectorielle
- fonction à valeur vectorielle
- une fonction de la forme\(\vecs r(t)=f(t)\hat{\mathbf{i}}+g(t)\hat{\mathbf{j}}\) ou\(\vecs r(t)=f(t)\hat{\mathbf{i}}+g(t)\hat{\mathbf{j}}+h(t)\hat{\mathbf{k}}\), lorsque le composant fonctionne\(f\)\(g\), et\(h\) sont des fonctions à valeur réelle du paramètre\(t\).
Contributeurs et attributions
- Template:ContribOpenStaxCalc
- Edited by Paul Seeburger (Monroe Community College)


