10.3E : Exercices pour la section 10.3

Polynômes de Taylor

Dans les exercices 1 à 8, trouvez les polynômes de Taylor de degré 2 se rapprochant de la fonction donnée centrée au point donné.

1)\( f(x)=1+x+x^2\) à\( a=1\)

2)\( f(x)=1+x+x^2\) à\( a=−1\)

Réponse

\( f(−1)=1;\;f′(−1)=−1;\;f''(−1)=2;\quad p_2(x)=1−(x+1)+(x+1)^2\)

3)\( f(x)=\cos(2x)\) à\( a=π\)

4)\( f(x)=\sin(2x)\) à\( a=\frac{π}{2}\)

Réponse

\( f′(x)=2\cos(2x);\;f''(x)=−4\sin(2x);\quad p_2(x)=−2(x−\frac{π}{2})\)

5)\( f(x)=\sqrt{x}\) à\( a=4\)

6)\( f(x)=\ln x\) à\( a=1\)

Réponse

\( f′(x)=\dfrac{1}{x};\; f''(x)=−\dfrac{1}{x^2};\quad p_2(x)=0+(x−1)−\frac{1}{2}(x−1)^2\)

7)\( f(x)=\dfrac{1}{x}\) à\( a=1\)

8)\( f(x)=e^x\) à\( a=1\)

Réponse

\( p_2(x)=e+e(x−1)+\dfrac{e}{2}(x−1)^2\)

Théorème du reste de Taylor

Dans les exercices 9 à 14, vérifiez que le choix donné,\(n\) dans l'estimation restante\( |R_n|≤\dfrac{M}{(n+1)!}(x−a)^{n+1}\), où\(M\) est la valeur maximale de\( ∣f^{(n+1)}(z)∣\) l'intervalle entre\(a\) et le point indiqué, donne des résultats\( |R_n|≤\frac{1}{1000}\). Détermine la valeur du polynôme\( p_n\) de Taylor de\( f\) au point indiqué.

9) [T]\( \sqrt{10};\; a=9,\; n=3\)

10) [T]\( (28)^{1/3};\; a=27,\; n=1\)

Réponse

\( \dfrac{d^2}{dx^2}x^{1/3}=−\dfrac{2}{9x^{5/3}}≥−0.00092…\)dans\( x≥28\) ce cas, l'estimation du reste s'applique à l'approximation linéaire\( x^{1/3}≈p_1(27)=3+\dfrac{x−27}{27}\), qui donne\( (28)^{1/3}≈3+\frac{1}{27}=3.\bar{037}\), tandis que\( (28)^{1/3}≈3.03658.\)

11) [T]\( \sin(6);\; a=2π,\; n=5\)

12) [T]\( e^2; \; a=0,\; n=9\)

Réponse

En utilisant l'estimation,\( \dfrac{2^{10}}{10!}<0.000283\) nous pouvons utiliser l'extension Taylor de l'ordre 9 pour estimer\( e^x\) à\( x=2\). comme\( e^2≈p_9(2)=1+2+\frac{2^2}{2}+\frac{2^3}{6}+⋯+\frac{2^9}{9!}=7.3887\)... alors que\( e^2≈7.3891.\)

13) [T]\( \cos(\frac{π}{5});\; a=0,\; n=4\)

14) [T]\( \ln(2);\; a=1,\; n=1000\)

Réponse

Depuis\( \dfrac{d^n}{dx^n}(\ln x)=(−1)^{n−1}\dfrac{(n−1)!}{x^n},R_{1000}≈\frac{1}{1001}\). On a\(\displaystyle p_{1000}(1)=\sum_{n=1}^{1000}\dfrac{(−1)^{n−1}}{n}≈0.6936\) alors\( \ln(2)≈0.6931⋯.\)

Approximation d'intégrales définies en utilisant la série Taylor

15) Intégrez l'approximation\(\sin t≈t−\dfrac{t^3}{6}+\dfrac{t^5}{120}−\dfrac{t^7}{5040}\) évaluée à\( π\) t pour obtenir une approximation\(\displaystyle ∫^1_0\frac{\sin πt}{πt}\,dt\).

16) Intégrer l'approximation\( e^x≈1+x+\dfrac{x^2}{2}+⋯+\dfrac{x^6}{720}\) évaluée\( −x^2\) à environ\(\displaystyle ∫^1_0e^{−x^2}\,dx.\)

Réponse

\(\displaystyle ∫^1_0\left(1−x^2+\frac{x^4}{2}−\frac{x^6}{6}+\frac{x^8}{24}−\frac{x^{10}}{120}+\frac{x^{12}}{720}\right)\,dx =1−\frac{1^3}{3}+\frac{1^5}{10}−\frac{1^7}{42}+\frac{1^9}{9⋅24}−\frac{1^{11}}{120⋅11}+\frac{1^{13}}{720⋅13}≈0.74683\)tandis que\(\displaystyle ∫^1_0e^{−x^2}dx≈0.74682.\)

Autres problèmes du théorème du reste de Taylor

Dans les exercices 17 à 20, trouvez la plus petite valeur de\(n\) telle sorte que l'estimation restante\( |R_n|≤\dfrac{M}{(n+1)!}(x−a)^{n+1}\), où\(M\) est la valeur maximale de\( ∣f^{(n+1)}(z)∣\) sur l'intervalle entre\(a\) et le point indiqué, donne\( |R_n|≤\frac{1}{1000}\) sur l'intervalle indiqué.

17)\( f(x)=\sin x\) sur\( [−π,π],\; a=0\)

18)\( f(x)=\cos x\) sur\( [−\frac{π}{2},\frac{π}{2}],\; a=0\)

Réponse

Depuis\( f^{(n+1)}(z)\) c'est\(\sin z\) ou\(\cos z\), nous l'avons fait\( M=1\). Depuis\( |x−0|≤\frac{π}{2}\), nous recherchons le plus petit\(n\) tel que\( \dfrac{π^{n+1}}{2^{n+1}(n+1)!}≤0.001\). La plus petite de ces valeurs est\( n=7\). Le reste de l'estimation est\( R_7≤0.00092.\)

19)\( f(x)=e^{−2x}\) sur\( [−1,1],a=0\)

20)\( f(x)=e^{−x}\) sur\( [−3,3],a=0\)

Réponse

Puisque\( f^{(n+1)}(z)=±e^{−z}\) l'un d'entre eux\( M=e^3\). Depuis\( |x−0|≤3\), on cherche le plus petit\(n\) tel que\( \dfrac{3^{n+1}e^3}{(n+1)!}≤0.001\). La plus petite de ces valeurs est\( n=14\). Le reste de l'estimation est\( R_{14}≤0.000220.\)

Dans les exercices 21 à 24, le maximum du côté droit de l'estimation du reste\( |R_1|≤\dfrac{max|f''(z)|}{2}R^2\)\( [a−R,a+R]\) se situe à\(a\) ou\( a±R\). Estimez la valeur maximale de\(R\) telle valeur\( \dfrac{max|f''(z)|}{2}R^2≤0.1\)\( [a−R,a+R]\) en traçant ce maximum en fonction de\(R\).

21) [T]\( e^x\) approximé par\( 1+x,\; a=0\)

22) [T]\( \sin x\) approximé par\( x,\; a=0\)

Réponse

Puisque\( \sin x\) augmente pour les petites entreprises\( x\) et depuis\( \frac{d^2}{dx^2}\left(\sin x\right)=−\sin x\), l'estimation s'applique à tout moment\( R^2\sin(R)≤0.2\), ce qui s'applique jusqu'à\( R=0.596.\)

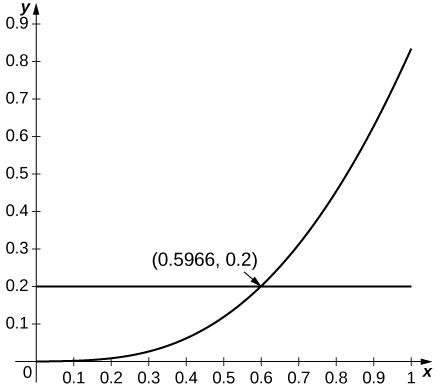
23) [T]\( \ln x\) approximé par\( x−1,\; a=1\)

24) [T]\( \cos x\) approximé par\( 1,\; a=0\)

Réponse

Puisque la dérivée seconde de\( \cos x\) est\( −\cos x\) et puisque\( \cos x\) diminue en s'éloignant de\( x=0\), l'estimation s'applique lorsque\( R^2\cos R≤0.2\) ou\( R≤0.447\).

Série Taylor

Dans les exercices 25 à 35, trouvez la série de Taylor de la fonction donnée centrée au point indiqué.

25)\(f(x) = x^4\) à\( a=−1\)

26)\(f(x) = 1+x+x^2+x^3\) à\( a=−1\)

Réponse

\( (x+1)^3−2(x+1)^2+2(x+1)\)

27)\(f(x) = \sin x\) à\( a=π\)

28)\(f(x) = \cos x\) à\( a=2π\)

Réponse

Les valeurs des dérivées sont les mêmes que pour\( x=0\) so\(\displaystyle \cos x=\sum_{n=0}^∞(−1)^n\frac{(x−2π)^{2n}}{(2n)!}\)

29)\(f(x) = \sin x\) à\( x=\frac{π}{2}\)

30)\(f(x) = \cos x\) à\( x=\frac{π}{2}\)

Réponse

\( \cos(\frac{π}{2})=0,\;−\sin(\frac{π}{2})=−1\)donc\(\displaystyle \cos x=\sum_{n=0}^∞(−1)^{n+1}\frac{(x−\frac{π}{2})^{2n+1}}{(2n+1)!}\), qui l'est également\( −\cos(x−\frac{π}{2})\).

31)\(f(x) = e^x\) à\( a=−1\)

32)\(f(x) = e^x\) à\( a=1\)

Réponse

Les dérivés le\( f^{(n)}(1)=e,\) sont\(\displaystyle e^x=e\sum_{n=0}^∞\frac{(x−1)^n}{n!}.\)

33)\(f(x) = \dfrac{1}{(x−1)^2}\) à\( a=0\) (Astuce : différenciez la série Taylor pour\( \dfrac{1}{1−x}\).)

34)\(f(x) = \dfrac{1}{(x−1)^3}\) à\( a=0\)

Réponse

\(\displaystyle \frac{1}{(x−1)^3}=−\frac{1}{2}\frac{d^2}{dx^2}\left(\frac{1}{1−x}\right)=−\sum_{n=0}^∞\left(\frac{(n+2)(n+1)x^n}{2}\right)\)

35)\(\displaystyle F(x)=∫^x_0\cos(\sqrt{t})\,dt;\quad \text{where}\; f(t)=\sum_{n=0}^∞(−1)^n\frac{t^n}{(2n)!}\) à a=0 (Remarque :\( f\) est la série Taylor de\(\cos(\sqrt{t}).)\)

Dans les exercices 36 à 44, calculez la série de Taylor de chaque fonction autour\( x=1\).

36)\( f(x)=2−x\)

Réponse

\( 2−x=1−(x−1)\)

(37)\( f(x)=x^3\)

38)\( f(x)=(x−2)^2\)

Réponse

\( ((x−1)−1)^2=(x−1)^2−2(x−1)+1\)

39)\( f(x)=\ln x\)

40)\( f(x)=\dfrac{1}{x}\)

Réponse

\(\displaystyle \frac{1}{1−(1−x)}=\sum_{n=0}^∞(−1)^n(x−1)^n\)

41)\( f(x)=\dfrac{1}{2x−x^2}\)

(42)\( f(x)=\dfrac{x}{4x−2x^2−1}\)

Réponse

\(\displaystyle x\sum_{n=0}^∞2^n(1−x)^{2n}=\sum_{n=0}^∞2^n(x−1)^{2n+1}+\sum_{n=0}^∞2^n(x−1)^{2n}\)

43)\( f(x)=e^{−x}\)

44)\( f(x)=e^{2x}\)

Réponse

\(\displaystyle e^{2x}=e^{2(x−1)+2}=e^2\sum_{n=0}^∞\frac{2^n(x−1)^n}{n!}\)

Série Maclaurin

[T] Dans les exercices 45 à 48, identifiez la valeur de\(x\) telle sorte que la série donnée\(\displaystyle \sum_{n=0}^∞a_n\) soit la valeur de la série de Maclaurin de\( f(x)\) at\( x\). Approximation de la valeur d'\( f(x)\)utilisation\(\displaystyle S_{10}=\sum_{n=0}^{10}a_n\).

45)\(\displaystyle \sum_{n=0}^∞\frac{1}{n!}\)

46)\(\displaystyle \sum_{n=0}^∞\frac{2^n}{n!}\)

Réponse

\( x=e^2;\quad S_{10}=\dfrac{34,913}{4725}≈7.3889947\)

47)\(\displaystyle \sum_{n=0}^∞\frac{(−1)^n(2π)^{2n}}{(2n)!}\)

48)\(\displaystyle \sum_{n=0}^∞\frac{(−1)^n(2π)^{2n+1}}{(2n+1)!}\)

Réponse

\(\sin(2π)=0;\quad S_{10}=8.27×10^{−5}\)

Dans les exercices 49 à 52, utilisez les fonctions\( S_5(x)=x−\dfrac{x^3}{6}+\dfrac{x^5}{120}\) et ainsi de\( C_4(x)=1−\dfrac{x^2}{2}+\dfrac{x^4}{24}\) suite\( [−π,π]\).

49) [T] Tracez\(\sin^2x−(S_5(x))^2\) sur\( [−π,π]\). Comparez la différence maximale avec le carré de l'estimation du reste de Taylor pour\( \sin x.\)

50) [T] Tracez\(\cos^2x−(C_4(x))^2\) sur\( [−π,π]\). Comparez la différence maximale avec le carré de l'estimation du reste de Taylor pour\( \cos x\).

Réponse

La différence est faible à l'intérieur de l'intervalle, mais elle se\( 1\) rapproche des extrémités. Le reste de l'estimation est\( |R_4|=\frac{π^5}{120}≈2.552.\)

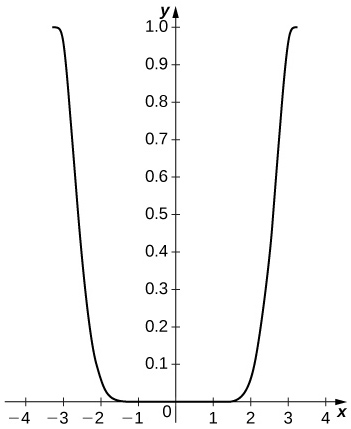
51) [T] Tracez\( |2S_5(x)C_4(x)−\sin(2x)|\) sur\( [−π,π]\).

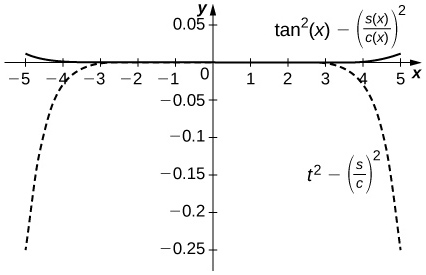
52) [T] Comparez\( \dfrac{S_5(x)}{C_4(x)}\)\( [−1,1]\) à\( \tan x\). Comparez cela avec l'estimation du reste de Taylor pour l'approximation de\( \tan x\) par\( x+\dfrac{x^3}{3}+\dfrac{2x^5}{15}\).

Réponse

La différence est de l'ordre de\( 10^{−4}\) on\( [−1,1]\) alors que l'erreur d'approximation de Taylor est\( 0.1\) proche\( ±1\). La courbe supérieure est un tracé de\(\tan^2x−\left(\dfrac{S_5(x)}{C_4(x)}\right)^2\) et le graphique en pointillés inférieur le montre\( t^2−\left(\dfrac{S_5}{C_4}\right)^2\).

53) [T]\( e^x−e_4(x)\) Tracez où\( e_4(x)=1+x+\dfrac{x^2}{2}+\dfrac{x^3}{6}+\dfrac{x^4}{24}\) sur\( [0,2]\). Comparez l'erreur maximale avec l'estimation du reste de Taylor.

54) (Approximations de Taylor et recherche des racines.) Rappelons que la méthode de Newton\( x_{n+1}=x_n−\dfrac{f(x_n)}{f'(x_n)}\) se rapproche des solutions situées à\( f(x)=0\) proximité de l'entrée\( x_0\).

a. Si\( f\) et\( g\) sont des fonctions inverses, expliquez pourquoi une solution de\( g(x)=a\) est la valeur\( f(a)\) de\( f\).

b.\( p_N(x)\) Soit le\( N^{\text{th}}\) degré polynomial de Maclaurin de\( e^x\). Utilisez la méthode de Newton pour approximer les solutions de\( p_N(x)−2=0\) pour\( N=4,5,6.\)

c. Expliquez pourquoi les racines approximatives de\( p_N(x)−2=0\) sont des valeurs approximatives de\(\ln(2).\)

Réponse

a. Les réponses peuvent varier.
b. Les valeurs suivantes sont les\( x_n\) valeurs après\( 10\) les itérations de la méthode de Newton pour approximer une racine de\( p_N(x)−2=0\) :\( N=4,x=0.6939...;\) for\( N=5,x=0.6932...;\) for for\( N=6,x=0.69315...;.\) (Note :\( \ln(2)=0.69314...\))
c. Les réponses peuvent varier.

Évaluation des limites en utilisant la série Taylor

Dans les exercices 55 à 58, utilisez le fait que si elle\(\displaystyle q(x)=\sum_{n=1}^∞a_n(x−c)^n\) converge dans un intervalle contenant\( c\), puis\(\displaystyle \lim_{x→c}q(x)=a_0\) pour évaluer chaque limite à l'aide de la série de Taylor.

55)\(\displaystyle \lim_{x→0}\frac{\cos x−1}{x^2}\)

56)\(\displaystyle \lim_{x→0}\frac{\ln(1−x^2)}{x^2}\)

Réponse

\( \dfrac{\ln(1−x^2)}{x^2}→−1\)

(57)\(\displaystyle \lim_{x→0}\frac{e^{x^2}−x^2−1}{x^4}\)

58)\(\displaystyle \lim_{x→0^+}\frac{\cos(\sqrt{x})−1}{2x}\)

Réponse

\(\displaystyle \frac{\cos(\sqrt{x})−1}{2x}≈\frac{(1−\frac{x}{2}+\frac{x^2}{4!}−⋯)−1}{2x}→−\frac{1}{4}\)