10.3 : Série Taylor et Maclaurin

Objectifs d'apprentissage

• Décrivez la procédure permettant de trouver un polynôme de Taylor d'un ordre donné pour une fonction.
• Expliquez la signification et la signification du théorème de Taylor avec le reste.
• Estimez le reste pour une approximation de la série de Taylor d'une fonction donnée.

Dans les deux sections précédentes, nous avons expliqué comment trouver des représentations de séries de puissances pour certains types de fonctions, en particulier les fonctions liées aux séries géométriques. Nous discutons ici des représentations des séries de puissances pour d'autres types de fonctions. Nous abordons en particulier les questions suivantes : Quelles fonctions peuvent être représentées par des séries de puissances et comment trouvons-nous de telles représentations ? Si nous pouvons trouver une représentation de série de puissances pour une fonction particulière\(f\) et que la série converge vers un certain intervalle, comment prouver que la série converge réellement vers\(f\) ?

Vue d'ensemble de la série Taylor/Maclaurin

Prenons l'exemple d'une fonction\(f\) dont la représentation en série de puissances est\(x=a\). Ensuite, la série a la forme

\[\sum_{n=0}^∞c_n(x−a)^n=c_0+c_1(x−a)+c_2(x−a)^2+ \dots. \label{eq1} \]

Quels devraient être les coefficients ? Pour l'instant, nous ignorons les questions de convergence, mais nous nous concentrons plutôt sur ce que devrait être la série, si elle existe. Nous reviendrons sur la convergence plus loin dans cette section. Si l'équation de la série \ ref {eq1} est une représentation de\(f\) at\(x=a\), nous voulons certainement que la série soit égale à\(f(a)\) at\(x=a\). En évaluant la série à\(x=a\), nous constatons que

\[\sum_{n=0}^∞c_n(x−a)^n=c_0+c_1(a−a)+c_2(a−a)^2+\dots=c_0.\label{eq2} \]

Ainsi, la série est\(f(a)\) égale au coefficient\(c_0=f(a)\). De plus, nous aimerions que la dérivée première de la série de puissances soit égale\(f′(a)\) à\(x=a\). En différenciant l'équation \ ref {eq2} terme par terme, nous voyons que

\[\dfrac{d}{dx}\left( \sum_{n=0}^∞c_n(x−a)^n \right)=c_1+2c_2(x−a)+3c_3(x−a)^2+\dots.\label{eq3} \]

Par conséquent, à\(x=a,\) la dérivée se trouve

\[\dfrac{d}{dx}\left( \sum_{n=0}^∞c_n(x−a)^n \right)=c_1+2c_2(a−a)+3c_3(a−a)^2+\dots=c_1.\label{eq4} \]

Par conséquent, la dérivée de la série est égale à\(f′(a)\) si le coefficient En\(c_1=f′(a).\) continuant ainsi, nous recherchons des coefficients\(c_n\) tels que toutes les dérivées de l'équation de la série de puissance \ ref {eq4} soient en accord avec toutes les dérivées correspondantes de\(f\) at\(x=a\). Les deuxième et troisième dérivées de l'équation \ ref {eq3} sont données par

\[\dfrac{d^2}{dx^2} \left(\sum_{n=0}^∞c_n(x−a)^n \right)=2c_2+3⋅2c_3(x−a)+4⋅3c_4(x−a)^2+\dots\label{eq5} \]

et

\[\dfrac{d^3}{dx^3} \left( \sum_{n=0}^∞c_n(x−a)^n \right)=3⋅2c_3+4⋅3⋅2c_4(x−a)+5⋅4⋅3c_5(x−a)^2+⋯.\label{eq6} \]

Par conséquent, at\(x=a\), les deuxième et troisième dérivées

\[\dfrac{d^2}{dx^2} \left(\sum_{n=0}^∞c_n(x−a)^n\right)=2c_2+3⋅2c_3(a−a)+4⋅3c_4(a−a)^2+\dots=2c_2\label{eq7} \]

et

\[\dfrac{d^3}{dx^3} \left(\sum_{n=0}^∞c_n(x−a)^n\right)=3⋅2c_3+4⋅3⋅2c_4(a−a)+5⋅4⋅3c_5(a−a)^2+\dots =3⋅2c_3\label{eq8} \]

égal\(f''(a)\) et\(f'''(a)\), respectivement, si\(c_2=\dfrac{f''(a)}{2}\) et\(c_3=\dfrac{f'''(a)}{3⋅2}\). Plus généralement, nous voyons que s'il\(f\) a une représentation en série de puissances à\(x=a\), alors les coefficients doivent être donnés par\(c_n=\dfrac{f^{(n)}(a)}{n!}\). C'est-à-dire que la série doit être

\[\sum_{n=0}^∞\dfrac{f^{(n)}(a)}{n!}(x−a)^n=f(a)+f′(a)(x−a)+\dfrac{f''(a)}{2!}(x−a)^2+\dfrac{f'''(a)}{3!}(x−a)^3+⋯ \nonumber \]

Cette série puissante pour\(f\) est connue sous le nom de série Taylor pour\(f\) at\(a.\) If\(x=0\), alors cette série est connue sous le nom de série Maclaurin pour\(f\).

Définition\(\PageIndex{1}\): Maclaurin and Taylor series

Si\(f\) possède des dérivées de tous les ordres at\(x=a\), alors la série de Taylor pour la fonction\(f\) at\(a\) est

\[\sum_{n=0}^∞\dfrac{f^{(n)}(a)}{n!}(x−a)^n=f(a)+f′(a)(x−a)+\dfrac{f''(a)}{2!}(x−a)^2+⋯+\dfrac{f^{(n)}(a)}{n!}(x−a)^n+⋯ \nonumber \]

La série Taylor pour\(f\) à 0 est connue sous le nom de série Maclaurin pour\(f\).

Plus loin dans cette section, nous montrerons des exemples de recherche de séries de Taylor et discuterons des conditions dans lesquelles la série de Taylor d'une fonction convergera vers cette fonction. Nous présentons ici un résultat important. Rappelons que les représentations des séries de puissance sont uniques. Par conséquent, si une fonction\(f\) possède une série de puissances à\(a\), il doit s'agir de la série Taylor pour\(f\) at\(a\).

Le caractère unique de la série Taylor

Si une fonction\(f\) possède une série de puissances à a qui converge vers\(f\) un intervalle ouvert contenant\(a\), alors cette série de puissances est la série Taylor pour\(f\) at\(a\).

La preuve découle directement de celle discutée précédemment.

Pour déterminer si une série de Taylor converge, nous devons examiner sa séquence de sommes partielles. Ces sommes partielles sont des polynômes finis, appelés polynômes de Taylor.

Polynômes de Taylor

La somme\(n^{\text{th}}\) partielle de la série de Taylor pour une fonction\(f\) at\(a\) est connue sous le nom de polynôme de Taylor à\(n^{\text{th}}\) -degré. ^{Par exemple, les 0 e, 1 er, 2 e et 3 e sommes partielles de la série de Taylor sont données par}

\[\begin{align*} p_0(x) &=f(a) \\[4pt] p_1(x) &=f(a)+f′(a)(x−a) \\[4pt]p_2(x) &=f(a)+f′(a)(x−a)+\dfrac{f''(a)}{2!}(x−a)^2\ \\[4pt]p_3(x) &=f(a)+f′(a)(x−a)+\dfrac{f''(a)}{2!}(x−a)^2+\dfrac{f'''(a)}{3!}(x−a)^3 \end{align*}\]

respectivement. Ces sommes partielles sont appelées polynômes de Taylor des 0 ^e, 1 ^er, 2 ^{e et 3 e} degrés de\(f\) at\(a\), respectivement. Si\(x=a\), alors ces polynômes sont connus sous le nom de polynômes de Maclaurin pour\(f\). Nous fournissons maintenant une définition formelle des polynômes de Taylor et de Maclaurin pour une fonction\(f\).

Définition\(\PageIndex{2}\): Maclaurin polynomial

Si\(f\) a\(n\) des dérivées à\(x=a\), alors le polynôme de Taylor à\(n^{\text{th}}\) -degré de\(f\) at\(a\) est

\[p_n(x)=f(a)+f′(a)(x−a)+\dfrac{f''(a)}{2!}(x−a)^2+\dfrac{f'''(a)}{3!}(x−a)^3+⋯+\dfrac{f^{(n)}(a)}{n!}(x−a)^n. \nonumber \]

Le polynôme de Taylor à\(n^{\text{th}}\) -degrés pour\(f\) at\(0\) est connu sous le nom de polynôme de Maclaurin à\(n^{\text{th}}\) degrés pour\(f\).

Nous montrons maintenant comment utiliser cette définition pour trouver plusieurs polynômes de Taylor pour\(f(x)=\ln x\) at\(x=1\).

Exemple\(\PageIndex{1}\): Finding Taylor Polynomials

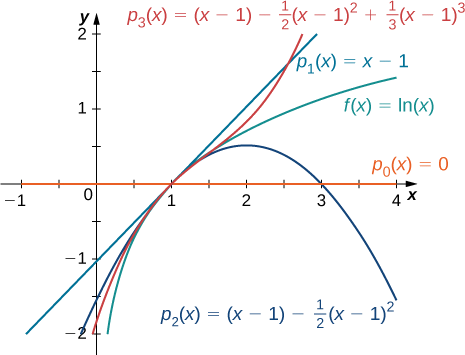
Trouvez les polynômes de Taylor\(p_0,p_1,p_2\) et\(p_3\) pour\(f(x)=\ln x\) at\(x=1\). Utilisez un utilitaire de création de graphiques pour comparer le graphe de\(f\) avec les graphes de\(p_0,p_1,p_2\) et\(p_3\).

Solution

Pour trouver ces polynômes de Taylor, nous devons évaluer\(f\) et évaluer ses trois premières dérivées à\(x=1\).

\ [\ begin {align*} f (x) &= \ ln x et f (1) &=0 \ \ [5 points]
f′ (x) &= \ dfrac {1} {x} et f′ (1) &=1 \ \ [5 points]
f « (x) &=− \ dfrac {1} {x^2} & f « (1) &=−1 \ [5 points]
f"' (x) &= \ dfrac {2} {x^3} & f"' (1) &=2 \ end {align*} \]

Par conséquent,

\[\begin{align*} p_0(x) &= f(1)=0,\\[4pt]p_1(x) &=f(1)+f′(1)(x−1) =x−1,\\[4pt]p_2(x) &=f(1)+f′(1)(x−1)+\dfrac{f''(1)}{2}(x−1)^2 = (x−1)−\dfrac{1}{2}(x−1)^2 \\[4pt]p_3(x) &=f(1)+f′(1)(x−1)+\dfrac{f''(1)}{2}(x−1)^2+\dfrac{f'''(1)}{3!}(x−1)^3=(x−1)−\dfrac{1}{2}(x−1)^2+\dfrac{1}{3}(x−1)^3 \end{align*}\]

Les graphes\(y=f(x)\) et les trois premiers polynômes de Taylor sont présentés sur la figure\(\PageIndex{1}\).

Figure\(\PageIndex{1}\) : La fonction\(y=\ln x\) et les polynômes de Taylor\(p_0,p_1,p_2\) et\(p_3\) at\(x=1\) sont tracés sur ce graphique.

Exercice\(\PageIndex{1}\)

Trouvez les polynômes de Taylor\(p_0,p_1,p_2\) et\(p_3\) pour\(f(x)=\dfrac{1}{x^2}\) at\(x=1\).

Allusion

Trouvez les trois premiers dérivés de\(f\) et évaluez-les sur\(x=1.\)

Réponse

\ [\ begin {align*} p_0 (x) &=1 \ \ [5 points]
p_1 (x) &=1−2 (x−1) \ \ [5 points]
p_2 (x) &=1−2 (x−1) +3 (x−1) ^2 \ \ [5 points]
p_3 (x) &=1−2 (x−1) +3 (x−1) −1) ^2−4 (x−1) ^3 \ end {align*} \]

Nous montrons maintenant comment trouver les polynômes de Maclaurin pour\(e^x, \sin x,\) et\(\cos x\). Comme indiqué ci-dessus, les polynômes de Maclaurin sont des polynômes de Taylor centrés à zéro.

Exemple\(\PageIndex{2}\): Finding Maclaurin Polynomials

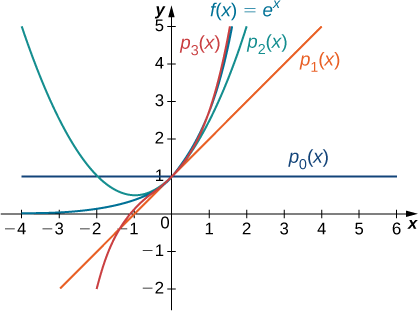
Pour chacune des fonctions suivantes, recherchez des formules pour les polynômes de Maclaurin\(p_0,p_1,p_2\) et\(p_3\). Trouvez une formule pour le polynôme de Maclaurin à\(n^{\text{th}}\) -degrés et écrivez-la en utilisant la notation sigma. Utilisez un utilitaire de création de graphiques pour comparer les graphes de\(p_0,p_1,p_2\) et\(p_3\) avec\(f\).

1. \(f(x)=e^x\)
2. \(f(x)=\sin x\)
3. \(f(x)=\cos x\)

Solution

Depuis\(f(x)=e^x\), nous le savons\(f(x)=f′(x)=f''(x)=⋯=f^{(n)}(x)=e^x\) pour tous les entiers positifs\(n\). Par conséquent,

\[f(0)=f′(0)=f''(0)=⋯=f^{(n)}(0)=1 \nonumber \]

pour tous les entiers positifs\(n\). Par conséquent, nous avons

\ (\ begin {align*} p_0 (x) &=f (0) =1, \ \ [5 points]
p_1 (x) &=f (0) +f′ (0) x=1+x, \ \ [5 points]
p_2 (x) &=f (0) +f′ (0) x+ \ dfrac {f « (0)} {2 !} x^2=1+x+ \ dfrac {1} {2} x^2, \ \ [5 points]
p_3 (x) &=f (0) +f′ (0) x+ \ dfrac {f « (0)} {2} x^2+ \ dfrac {f"' (0)} {3 !} x^3=1+x+ \ dfrac {1} {2} x^2+ \ dfrac {1} {3 !} x^3, \ end {align*} \)

\ (\ displaystyle \ begin {align*} p_n (x) &=f (0) +f′ (0) x+ \ dfrac {f « (0)} {2} x^2+ \ dfrac {f"' (0)} {3 !} x^3++ \ dfrac {f^ {(n)} (0)} {n !} x^n \ \ [5 points]
&=1+x+ \ dfrac {x^2} {2 !} + \ dfrac {x^3} {3 !} + \ dfrac {x^n} {n !} \ \ [5 points]
&= \ sum_ {k=0} ^n \ dfrac {x^k} {k !} \ end {align*} \).

La fonction et les trois premiers polynômes de Maclaurin sont illustrés sur la figure\(\PageIndex{2}\).

Figure\(\PageIndex{2}\) : Le graphique montre la fonction\(y=e^x\) et les polynômes de Maclaurin\(p_0,\,p_1,\,p_2\) et\(p_3\).

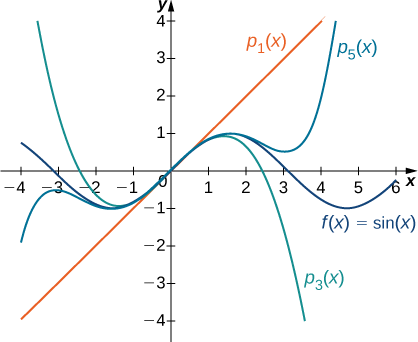
b. Pour\(f(x)=\sin x\), les valeurs de la fonction et de ses quatre premières dérivées at\(x=0\) sont données comme suit :

\ [\ begin {align*} f (x) &= \ sin x et f (0) &=0 \ \ [5 points]
f′ (x) &= \ cos x et f′ (0) &=1 \ \ [5 points]
f « (x) &=− \ sin x & f « (0) &=0 \ \ [5 points]
f"' (x) &=− \ cos x & f"' (0) &=−1 \ \ [5 points]
f^ {(4)} (x) &= \ sin x & f^ {(4)} (0) &=0. \ end {align*} \]

Puisque la quatrième dérivée est\(\sin x,\) le schéma se répète. C'est-à-dire,\(f^{(2m)}(0)=0\) et\(f^{(2m+1)}(0)=(−1)^m\) pour\(m≥0.\) Ainsi, nous avons

\ (\ begin {align*} p_0 (x) &=0, \ \ [5 points]
p_1 (x) &=0+x=x, \ \ [5 points]
p_2 (x) &=0+x+0=x, \ \ [5 points]
p_3 (x) &=0+x+0− \ dfrac {1} {3 !} x^3=x− \ dfrac {x^3} {3 !} , \ \ [5 points]
p_4 (x) &=0+x+0− \ dfrac {1} {3 !} x^3+0=x− \ dfrac {x^3} {3 !} , \ \ [5 points]
p_5 (x) &=0+x+0− \ dfrac {1} {3 !} x^3+0+ \ dfrac {1} {5 !} x^5=x− \ dfrac {x^3} {3 !} + \ dfrac {x^5} {5 !} , \ end {align*} \)

et pour\(m≥0\),

\ [\ begin {align*} p_ {2m+1} (x) =p_ {2m+2} (x) &=x− \ dfrac {x^3} {3 !} + \ dfrac {x^5} {5 !} −+ (−1) ^m \ dfrac {x^ {2 m+1}} {(2 m+1) !} \ \ [5 points]
&= \ sum_ {k=0} ^m (−1) ^k \ dfrac {x^ {2 k+1}} {(2 k+1) !}. \ end {align*} \]

Les graphes de la fonction et de ses polynômes de Maclaurin sont présentés sur la figure\(\PageIndex{3}\).

Figure\(\PageIndex{3}\) : Le graphique montre la fonction\(y=\sin x\) et les polynômes de Maclaurin\(p_1,\, p_3\) et\(p_5\).

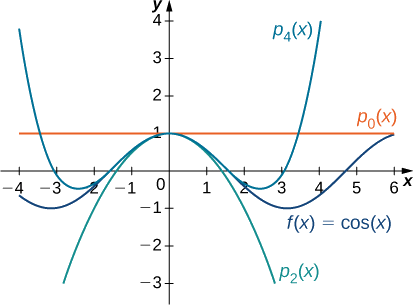
c. Pour\(f(x)=\cos x\), les valeurs de la fonction et de ses quatre premières dérivées at\(x=0\) sont données comme suit :

\ [\ begin {align*} f (x) &= \ cos x et f (0) &=1 \ \ [5 points]
f′ (x) &=− \ sin x & f′ (0) &=0 \ \ [5 points]
f « (x) &=− \ cos x & f « (0) &=−1 \ \ [5 points]
f"' (x) &= \ sin x & f"' (0) &=0 \ \ [5 points]
f^ {(4)} (x) &= \ cos x & f^ {(4)} (0) &=1. \ end {align*} \]

Puisque la quatrième dérivée est\(\sin x\), le motif se répète. En d'autres termes,\(f^{(2m)}(0)=(−1)^m\) et\(f^{(2m+1)}=0\) pour\(m≥0\). Par conséquent,

\ (\ begin {align*} p_0 (x) &=1, \ \ [5 points]
p_1 (x) &=1+0=1, \ \ [5 points]
p_2 (x) &=1+0− \ dfrac {1} {2 !} x^2=1− \ dfrac {x^2} {2 !} , \ \ [5 points]
p_3 (x) &=1+0− \ dfrac {1} {2 !} x^2+0=1− \ dfrac {x^2} {2 !} , \ \ [5 points]
p_4 (x) &=1+0− \ dfrac {1} {2 !} x^2+0+ \ dfrac {1} {4 !} x^4=1− \ dfrac {x^2} {2 !} + \ dfrac {x^4} {4 !} , \ \ [5 points]
p_5 (x) &=1+0− \ dfrac {1} {2 !} x^2+0+ \ dfrac {1} {4 !} x^4+0=1− \ dfrac {x^2} {2 !} + \ dfrac {x^4} {4 !} , \ end {align*} \)

et pour\(n≥0\),

\ [\ begin {align*} p_ {2 m} (x) &=p_ {2 m+1} (x) \ \ [5 points]
&=1− \ dfrac {x^2} {2 !} + \ dfrac {x^4} {4 !} −+ (−1) ^m \ dfrac {x^ {2 m}} {(2 m) !} \ \ [5 points]
&= \ sum_ {k=0} ^m (−1) ^k \ dfrac {x^ {2 k}} {(2 k) !}. \ end {align*} \]

Les graphes de la fonction et des polynômes de Maclaurin apparaissent sur la figure\(\PageIndex{4}\).

Figure\(\PageIndex{4}\) : La fonction\(y=\cos x\) et les polynômes\(p_0,p_2\) de Maclaurin\(p_4\) sont tracés sur ce graphique.

Exercice\(\PageIndex{2}\)

Trouvez des formules pour les polynômes de Maclaurin\(p_0,\,p_1,\,p_2\) et\(p_3\) pour\(f(x)=\dfrac{1}{1+x}\).

Trouvez une formule pour le\(n^{\text{th}}\) polynôme de Maclaurin à degrés. Écrivez votre réponse en utilisant la notation sigma.

Allusion

Évaluez les quatre premières dérivées de\(f\) et recherchez un modèle.

Réponse

\(\displaystyle p_0(x)=1;\;p_1(x)=1−x;\;p_2(x)=1−x+x^2;\;p_3(x)=1−x+x^2−x^3;\;p_n(x)=1−x+x^2−x^3+⋯+(−1)^nx^n=\sum_{k=0}^n(−1)^kx^k\)

Théorème de Taylor avec reste

Rappelez-vous que le polynôme de Taylor à\(n^{\text{th}}\) -degré pour une fonction\(f\) at\(a\) est la somme\(n^{\text{th}}\) partielle de la série de Taylor pour\(f\) at\(a\). Par conséquent, pour déterminer si la série de Taylor converge, nous devons déterminer si la séquence des polynômes de Taylor\({p_n}\) converge. Cependant, non seulement nous voulons savoir si la séquence des polynômes de Taylor converge, mais nous voulons également savoir si elle converge vers\(f\). Pour répondre à cette question, nous définissons le reste\(R_n(x)\) comme

\[R_n(x)=f(x)−p_n(x). \nonumber \]

Pour que la séquence des polynômes de Taylor converge\(f\), il faut que le reste converge\(R_n\) vers zéro. Pour déterminer si elle\(R_n\) converge vers zéro, nous introduisons le théorème de Taylor avec le reste. Ce théorème est non seulement utile pour prouver qu'une série de Taylor converge vers sa fonction associée, mais il nous permettra également de quantifier dans quelle mesure le polynôme de Taylor à\(n^{\text{th}}\) -degré se rapproche de la fonction.

Ici, nous cherchons une limite sur\(|R_n|.\) Considérez le cas le plus simple :\(n=0\). \(p_0\)Soit le 0 ^{ème acte} polynomial de Taylor\(a\) pour une fonction\(f\). Le reste\(R_0\) satisfait

\(R_0(x)=f(x)−p_0(x)=f(x)−f(a).\)

\(f\)Il est dérivable sur un intervalle\(I\) contenant\(a\) et\(x\), alors selon le théorème de la valeur moyenne, il existe un nombre réel\(c\) entre\(a\) et\(x\) tel que\(f(x)−f(a)=f′(c)(x−a)\). Par conséquent,

\[R_0(x)=f′(c)(x−a). \nonumber \]

En utilisant le théorème de la valeur moyenne dans un argument similaire, nous pouvons montrer que si\(f\) est dérivable en\(n\) temps sur un intervalle\(I\) contenant\(a\) et\(x\), alors le\(n^{\text{th}}\) reste\(R_n\) satisfait

\[R_n(x)=\dfrac{f^{(n+1)}(c)}{(n+1)!}(x−a)^{n+1} \nonumber \]

pour un nombre réel\(c\) compris entre\(a\) et\(x\). Il est important de noter que la valeur\(c\) du numérateur ci-dessus n'est pas le centre\(a\), mais plutôt une valeur inconnue\(c\) comprise entre\(a\) et\(x\). Cette formule nous permet d'obtenir une limite sur le reste\(R_n\). S'il nous arrive de savoir que\(∣f^{(n+1)}(x)∣\) c'est limité par un nombre réel\(M\) sur cet intervalle\(I\), alors

\[|R_n(x)|≤\dfrac{M}{(n+1)!}|x−a|^{n+1} \nonumber \]

pour tous\(x\) dans l'intervalle\(I\).

Nous énonçons maintenant le théorème de Taylor, qui fournit la relation formelle entre une fonction\(f\) et son polynôme de Taylor à\(n^{\text{th}}\) degrés\(p_n(x)\). Ce théorème nous permet de limiter l'erreur lors de l'utilisation d'un polynôme de Taylor pour approximer la valeur d'une fonction, et sera important pour prouver qu'une série de Taylor pour\(f\) converge vers\(f\).

Théorème de Taylor avec reste

Soit\(f\) une fonction qui peut être différenciée en\(n+1\) temps sur un intervalle\(I\) contenant le nombre réel\(a\). \(p_n\)Soit le\(n^{\text{th}}\) polynôme de Taylor en -degrés de\(f\) at\(a\) et let

\[R_n(x)=f(x)−p_n(x) \nonumber \]

soit le\(n^{\text{th}}\) reste. Ensuite, pour chaque\(x\) élément de l'intervalle\(I\), il existe un nombre réel\(c\) compris entre\(a\) et\(x\) tel que

\[R_n(x)=\dfrac{f^{(n+1)}(c)}{(n+1)!}(x−a)^{n+1} \nonumber \].

S'il existe un nombre réel\(M\) tel que\(∣f^{(n+1)}(x)∣≤M\) pour tous\(x∈I\), alors

\[|R_n(x)|≤\dfrac{M}{(n+1)!}|x−a|^{n+1} \nonumber \]

pour tous\(x\)\(I\).

Une preuve

Fixez un point\(x∈I\) et introduisez la fonction de\(g\) telle sorte que

\[g(t)=f(x)−f(t)−f′(t)(x−t)−\dfrac{f''(t)}{2!}(x−t)^2−⋯−\dfrac{f^{(n)}(t)}{n!}(x−t)^n−R_n(x)\dfrac{(x−t)^{n+1}}{(x−a)^{n+1}}. \nonumber \]

Nous prétendons que cela\(g\) répond aux critères du théorème de Rolle. Comme\(g\) il s'agit d'une fonction polynomiale (in\(t\)), c'est une fonction dérivable. De plus,\(g\) est zéro à\(t=a\) et\(t=x\) parce que

\[ \begin{align*} g(a) &=f(x)−f(a)−f′(a)(x−a)−\dfrac{f''(a)}{2!}(x−a)^2+⋯+\dfrac{f^{(n)}(a)}{n!}(x−a)^n−R_n(x) \\[4pt] &=f(x)−p_n(x)−R_n(x) \\[4pt] &=0, \\[4pt] g(x) &=f(x)−f(x)−0−⋯−0 \\[4pt] &=0. \end{align*}\]

Par conséquent,\(g\) satisfait le théorème de Rolle, et par conséquent, il existe\(c\) entre\(a\) et\(x\) tel que\(g′(c)=0.\) Nous calculons maintenant\(g′\). En utilisant la règle du produit, nous remarquons que

\[\dfrac{d}{dt}\left[\dfrac{f^{(n)}(t)}{n!}(x−t)^n\right]=−\dfrac{f^{(n)}(t)}{(n−1)!}(x−t)^{n−1}+\dfrac{f^{(n+1)}(t)}{n!}(x−t)^n. \nonumber \]

Par conséquent,

\ [\ begin {align} g′ (t) &=−f′ (t) + [f′ (t) −f « (t) (x−t)] + \ left [f » (t) (x−t) − \ dfrac {f"' (t)} {2 !} (x−t) ^2 \ right] +\ nonumber \ \
& \ quad+ \ left [\ dfrac {f^ {(n)} (t)} {(n−1) !} (x−t) ^ {n−1} − \ dfrac {f^ {(n+1)} (t)} {n !} (x−t) ^n \ right] + (n+1) R_n (x) \ dfrac {(x−t) ^n} {(x−a) ^ {n+1}} \ end {align} \ nonnumber \].

Remarquez qu'il y a un effet télescopique. Par conséquent,

\[g'(t)=−\dfrac{f^{(n+1)}(t)}{n!}(x−t)^n+(n+1)R_n(x)\dfrac{(x−t)^n}{(x−a)^{n+1}} \nonumber \].

Par le théorème de Rolle, nous concluons qu'il existe un nombre\(c\) entre\(a\) et\(x\) tel\(g′(c)=0.\) que

\[g′(c)=−\dfrac{f^{(n+1})(c)}{n!}(x−c)^n+(n+1)R_n(x)\dfrac{(x−c)^n}{(x−a)^{n+1}} \nonumber \]

nous concluons que

\[−\dfrac{f^{(n+1)}(c)}{n!}(x−c)^n+(n+1)R_n(x)\dfrac{(x−c)^n}{(x−a)^{n+1}}=0. \nonumber \]

En ajoutant le premier terme sur le côté gauche aux deux côtés de l'équation et en divisant les deux côtés de l'équation par,\(n+1,\) nous concluons que

\[R_n(x)=\dfrac{f^{(n+1)}(c)}{(n+1)!}(x−a)^{n+1} \nonumber \]

comme vous le souhaitez. De ce fait, il s'ensuit que s'il existe\(M\) une telle\(∣f^{(n+1)}(x)∣≤M\) situation pour tous\(x\)\(I\), alors

\[|R_n(x)|≤\dfrac{M}{(n+1)!}|x−a|^{n+1} \nonumber \].

□

Non seulement le théorème de Taylor nous permet de prouver qu'une série de Taylor converge vers une fonction, mais il nous permet également d'estimer la précision des polynômes de Taylor lors de l'approximation des valeurs des fonctions. Nous commençons par examiner les approximations linéaires et quadratiques de\(f(x)=\sqrt[3]{x}\) at\(x=8\) et déterminons la précision de ces approximations lors de l'estimation\(\sqrt[3]{11}\).

Exemple\(\PageIndex{3}\): Using Linear and Quadratic Approximations to Estimate Function Values

Réfléchissez à la fonction\(f(x)=\sqrt[3]{x}\).

1. Trouvez les premier et deuxième polynômes de Taylor pour\(f\) at\(x=8\). Utilisez un utilitaire de création graphique pour comparer ces polynômes avec\(f\) des\(x=8.\)
2. Utilisez ces deux polynômes pour effectuer une estimation\(\sqrt[3]{11}\).
3. Utilisez le théorème de Taylor pour limiter l'erreur.

Solution :

a. Pour\(f(x)=\sqrt[3]{x}\), les valeurs de la fonction et de ses deux premières dérivées at\(x=8\) sont les suivantes :

\ [\ begin {align*} f (x) &= \ sqrt [3] {x} et f (8) &=2 \ \ [5 points] f′ (x) &= \ dfrac {1} {3x^ {2/3}}, &
f′ (8) &= \ dfrac {1} {12} \ \ [5 points] f « (x) &= \ dfrac {1} {12} \ \ [5 points]
f « (x) &= \ dfrac {1} {12} \ \ [5 points] f « (x) &= \ dfrac ac {−2} {9x^ {5/3}}, & f « (8) &=− \ dfrac {1} {144.} \ end {align*} \]

Ainsi, les premier et deuxième polynômes de Taylor à\(x=8\) sont donnés par

\ (\ begin {align*} p_1 (x) &=f (8) +f′ (8) (x−8) \ \ [5 points]
&=2+ \ dfrac {1} {12} (x−8) \ end {align*} \)

\ (\ begin {align*} p_2 (x) &=f (8) +f′ (8) (x−8) + \ dfrac {f « (8)} {2 !} (x−8) ^2 \ \ [5 points]
&=2+ \ dfrac {1} {12} (x−8) − \ dfrac {1} {288} (x−8) ^2. \ end {align*} \)

La fonction et les polynômes de Taylor sont illustrés sur la figure\(\PageIndex{5}\).

Figure\(\PageIndex{5}\) : Les graphes\(f(x)=\sqrt[3]{x}\) et les approximations linéaires et quadratiques\(p_1(x)\) et\(p_2(x)\)

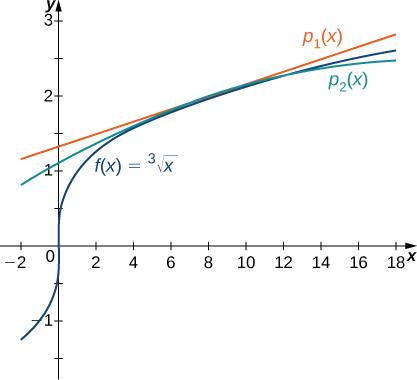
b. En utilisant le premier polynôme de Taylor à\(x=8\), nous pouvons estimer

\[\sqrt[3]{11}≈p_1(11)=2+\dfrac{1}{12}(11−8)=2.25. \nonumber \]

En utilisant le deuxième polynôme de Taylor à\(x=8\), nous obtenons

\[\sqrt[3]{11}≈p_2(11)=2+\dfrac{1}{12}(11−8)−\dfrac{1}{288}(11−8)^2=2.21875. \nonumber \]

c. Par note, il existe un c dans l'intervalle de\((8,11)\) telle sorte que le reste, lorsqu'on l'\(\sqrt[3]{11}\)approxime par le premier polynôme de Taylor, satisfait

\[R_1(11)=\dfrac{f''(c)}{2!}(11−8)^2. \nonumber \]

Nous ne connaissons pas la valeur exacte de\(c,\), nous trouvons donc une limite supérieure\(R_1(11)\) en déterminant la valeur maximale de\(f''\) sur l'intervalle\((8,11)\). Puisque\(f''(x)=−\dfrac{2}{9x^{5/3}}\), la valeur la plus élevée pour\(|f''(x)|\) cet intervalle se trouve à\(x=8\). En utilisant le fait que\(f''(8)=−\dfrac{1}{144}\), nous obtenons

\(|R_1(11)|≤\dfrac{1}{144⋅2!}(11−8)^2=0.03125.\)

De même, pour estimer\(R_2(11)\), nous utilisons le fait que

\(R_2(11)=\dfrac{f'''(c)}{3!}(11−8)^3\).

Depuis\(f'''(x)=\dfrac{10}{27x^{8/3}}\), la valeur maximale de\(f'''\) sur l'intervalle\((8,11)\) est\(f'''(8)≈0.0014468\). Par conséquent, nous avons

\(|R_2(11)|≤\dfrac{0.0011468}{3!}(11−8)^3≈0.0065104.\)

Exercice\(\PageIndex{3}\):

Trouvez les premier et deuxième polynômes de Taylor pour\(f(x)=\sqrt{x}\) at\(x=4\). Utilisez ces polynômes pour effectuer des estimations\(\sqrt{6}\). Utilisez le théorème de Taylor pour limiter l'erreur.

Allusion

Évaluer\(f(4),f′(4),\) et\(f''(4).\)

Réponse

\(p_1(x)=2+\dfrac{1}{4}(x−4);p_2(x)=2+\dfrac{1}{4}(x−4)−\dfrac{1}{64}(x−4)^2;p_1(6)=2.5;p_2(6)=2.4375;\)

\(|R_1(6)|≤0.0625;|R_2(6)|≤0.015625\)

Exemple\(\PageIndex{4}\): Approximating \(\sin x\) Using Maclaurin Polynomials

À partir de l'exemple\(\PageIndex{2b}\), les polynômes de Maclaurin pour\(\sin x\) sont donnés par

\[p_{2m+1}(x)=p_{2m+2}(x)=x−\dfrac{x^3}{3!}+\dfrac{x^5}{5!}−\dfrac{x^7}{7!}+⋯+(−1)^m\dfrac{x^{2m+1}}{(2m+1)!} \nonumber \]

pour\(m=0,1,2,….\)

1. Utilisez le cinquième polynôme de Maclaurin\(\sin x\) pour approximer\(\sin\left(\dfrac{π}{18}\right)\) et limiter l'erreur.
2. Pour quelles valeurs le cinquième polynôme de\(x\) Maclaurin se rapproche-t-il\(\sin x\) de l'intérieur\(0.0001\) ?

Solution

un.

Le cinquième polynôme de Maclaurin est

\[p_5(x)=x−\dfrac{x^3}{3!}+\dfrac{x^5}{5!} \nonumber \].

À l'aide de ce polynôme, nous pouvons estimer comme suit :

\[\sin\left(\dfrac{π}{18}\right)≈p_5\left(\dfrac{π}{18}\right)=\dfrac{π}{18}−\dfrac{1}{3!}\left(\dfrac{π}{18}\right)^3+\dfrac{1}{5!}\left(\dfrac{π}{18}\right)^5≈0.173648. \nonumber \]

Pour estimer l'erreur, utilisez le fait que le sixième polynôme de Maclaurin est\(p_6(x)=p_5(x)\) et calculez une borne sur\(R_6(\dfrac{π}{18})\). Par remarque, le reste est

\[R_6\left(\dfrac{π}{18}\right)=\dfrac{f^{(7)}(c)}{7!}\left(\dfrac{π}{18}\right)^7 \nonumber \]

pour certains\(c\) entre 0 et\(\dfrac{π}{18}\). En utilisant le fait que,\(∣f^{(7)}(x)∣≤1\) pour tous\(x\), nous constatons que l'ampleur de l'erreur est tout au plus

\[\dfrac{1}{7!}⋅\left(\dfrac{π}{18}\right)^7≤9.8×10^{−10}. \nonumber \]

b.

Nous devons trouver les valeurs d'\(x\)une telle

\[\dfrac{1}{7!}|x|^7≤0.0001. \nonumber \]

En résolvant cette inégalité pour\(x\), nous avons que le cinquième polynôme de Maclaurin donne une estimation à l'intérieur\(0.0001\) tant que\(|x|<0.907.\)

Exercice\(\PageIndex{4}\)

Utilisez le quatrième polynôme de Maclaurin\(\cos x\) pour approximer\(\cos\left(\dfrac{π}{12}\right).\)

Allusion

Le quatrième polynôme de Maclaurin est\(p_4(x)=1−\dfrac{x^2}{2!}+\dfrac{x^4}{4!}\).

Réponse

0,96593

Maintenant que nous sommes en mesure de relier le reste\(R_n(x)\), nous pouvons utiliser cette borne pour prouver qu'une série Taylor pour\(f\) at a converge vers\(f\).

Représenter des fonctions avec les séries Taylor et Maclaurin

Nous discutons maintenant des problèmes de convergence pour la série Taylor. Nous commençons par montrer comment trouver une série de Taylor pour une fonction et comment déterminer son intervalle de convergence.

Exemple\(\PageIndex{5}\): Finding a Taylor Series

Retrouvez la série Taylor pour\(f(x)=\dfrac{1}{x}\) chez\(x=1\). Déterminez l'intervalle de convergence.

Solution

Pour\(f(x)=\dfrac{1}{x},\) les valeurs de la fonction et de ses quatre premières\(x=1\) dérivées à

\ [\ begin {align*} f (x) &= \ dfrac {1} {x} & f (1) &=1 \ \ [5 points]
f′ (x) &=− \ dfrac {1} {x^2} & f′ (1) &=−1 \ \ [5 points]
f « (x) &= \ dfrac {2} {x^3} & f « (1) &=2 ! \ \ [5 points]
f"' (x) &=− \ dfrac {3⋅2} {x^4} & f"' (1) &=−3 ! \ \ [5 points]
f^ {(4)} (x) &= \ dfrac {4⋅3⋅2} {x^5} et f^ {(4)} (1) &=4 !. \ end {align*} \]

C'est-à-dire que nous en avons\(f^{(n)}(1)=(−1)^nn!\) pour tous\(n≥0\). Par conséquent, la série Taylor pour\(f\) at\(x=1\) est donnée par

\(\displaystyle \sum_{n=0}^∞\dfrac{f^{(n)}(1)}{n!}(x−1)^n=\sum_{n=0}^∞(−1)^n(x−1)^n\).

Pour déterminer l'intervalle de convergence, nous utilisons le test du ratio. Nous constatons que

\(\dfrac{|a_{n+1}|}{|a_n|}=\dfrac{∣(−1)^{n+1}(x−1)n^{+1}∣}{|(−1)^n(x−1)^n|}=|x−1|\).

Ainsi, la série converge si\(|x−1|<1.\) c'est le cas, la série converge pour\(0<x<2\). Ensuite, nous devons vérifier les points de terminaison. À\(x=2\), on voit que

\(\displaystyle \sum_{n=0}^∞(−1)^n(2−1)^n=\sum_{n=0}^∞(−1)^n\)

diverge selon le test de divergence. De même, à\(x=0,\)

\(\displaystyle \sum_{n=0}^∞(−1)^n(0−1)^n=\sum_{n=0}^∞(−1)^{2n}=\sum_{n=0}^∞1\)

diverge. Par conséquent, l'intervalle de convergence est\((0,2)\).

Exercice\(\PageIndex{5}\)

Trouvez la série de Taylor pour\(f(x)=\dfrac{1}{2}\) at\(x=2\) et déterminez son intervalle de convergence.

Allusion

\(f^{(n)}(2)=\dfrac{(−1)^nn!}{2^{n+1}}\)

Réponse

\(\dfrac{1}{2}\displaystyle \sum_{n=0}^∞\left(\dfrac{2−x}{2}\right)^n\). L'intervalle de convergence est\((0,4)\).

Nous savons que la série Taylor trouvée dans cet exemple converge vers l'intervalle\((0,2)\), mais comment savons-nous vers laquelle elle converge réellement\(f\) ? Nous examinerons cette question de manière plus générale dans un instant, mais pour cet exemple, nous pouvons répondre à cette question en écrivant

\[ f(x)=\dfrac{1}{x}=\dfrac{1}{1−(1−x)}. \nonumber \]

C'est-à-dire qu'elle\(f\) peut être représentée par la série géométrique\(\displaystyle \sum_{n=0}^∞(1−x)^n\). Comme il s'agit d'une série géométrique, elle converge\(\dfrac{1}{x}\) aussi longtemps que.\(|1−x|<1.\) Par conséquent, la série Taylor trouvée dans l'exemple converge vers\(f(x)=\dfrac{1}{x}\)\((0,2).\)

Nous examinons maintenant la question plus générale : si une série de Taylor pour une fonction\(f\) converge vers un certain intervalle, comment pouvons-nous déterminer si elle converge réellement vers\(f\) ? Pour répondre à cette question, rappelons qu'une série converge vers une valeur particulière si et seulement si sa séquence de sommes partielles converge vers cette valeur. Étant donné une série de Taylor pour\(f\) at\(a\), la somme\(n^{\text{th}}\) partielle est donnée par le polynôme de Taylor à\(n^{\text{th}}\) -degré\(p_n\). Par conséquent, pour déterminer si la série Taylor converge vers\(f\), nous devons déterminer si

\(\displaystyle \lim_{n→∞}p_n(x)=f(x)\).

Depuis le reste\(R_n(x)=f(x)−p_n(x)\), la série Taylor converge vers\(f\) si et seulement si

\(\displaystyle \lim_{n→∞}R_n(x)=0.\)

Nous énonçons maintenant formellement ce théorème.

Série Convergence de Taylor

Supposons qu'il\(f\) possède des dérivées de tous les ordres sur un intervalle\(I\) contenant\(a\). Puis la série Taylor

\[\sum_{n=0}^∞\dfrac{f^{(n)}(a)}{n!}(x−a)^n \nonumber \]

converge vers\(f(x)\) for all\(x\) in\(I\) if et only if

\[\lim_{n→∞}R_n(x)=0 \nonumber \]

pour tous\(x\)\(I\).

Avec ce théorème, nous pouvons prouver qu'une série de Taylor pour\(f\) at a converge vers\(f\) si nous pouvons prouver que le reste\(R_n(x)→0\). Pour le prouver\(R_n(x)→0\), nous utilisons généralement la borne

\[|R_n(x)|≤\dfrac{M}{(n+1)!}|x−a|^{n+1} \nonumber \]

du théorème de Taylor avec le reste.

Dans l'exemple suivant, nous trouvons la série de Maclaurin pour\(e^x\) et\(\sin x\) et montrons que ces séries convergent vers les fonctions correspondantes pour tous les nombres réels en prouvant que les restes\(R_n(x)→0\) pour tous les nombres réels\(x\).

Exemple\(\PageIndex{6}\): Finding Maclaurin Series

Pour chacune des fonctions suivantes, trouvez la série de Maclaurin et son intervalle de convergence. Utilisez Note pour prouver que la série de Maclaurin pour\(f\) converge vers\(f\) cet intervalle.

1. \(e^x\)
2. \(\sin x\)

Solution

a. En utilisant le polynôme de Maclaurin à\(n^{\text{th}}\) -degré\(e^x\) trouvé dans l'exemple a., nous trouvons que la série de Maclaurin pour\(e^x\) est donnée par

\(\displaystyle \sum_{n=0}^∞\dfrac{x^n}{n!}\).

Pour déterminer l'intervalle de convergence, nous utilisons le test du ratio. Depuis

\(\dfrac{|a_{n+1}|}{|a_n|}=\dfrac{|x|^{n+1}}{(n+1)!}⋅\dfrac{n!}{|x|^n}=\dfrac{|x|}{n+1}\),

nous avons

\(\displaystyle \lim_{n→∞}\dfrac{|a_{n+1}|}{|a_n|}=\lim_{n→∞}\dfrac{|x|}{n+1}=0\)

pour tous\(x\). Par conséquent, la série converge absolument pour tous\(x\), et donc l'intervalle de convergence est\((−∞,∞)\). Pour montrer que la série converge vers\(e^x\) pour tous\(x\), nous utilisons le fait que\(f^{(n)}(x)=e^x\) pour tous\(n≥0\) et\(e^x\) est une fonction croissante sur\((−∞,∞)\). Par conséquent, pour tout nombre réel\(b\), la valeur maximale de\(e^x\) pour tous\(|x|≤b\) est\(e^b\). Ainsi,

\(|R_n(x)|≤\dfrac{e^b}{(n+1)!}|x|^{n+1}\).

Puisque nous venons de montrer que

\(\displaystyle \sum_{n=0}^∞\dfrac{|x|^n}{n!}\)

converge pour tous\(x\), par le test de divergence, nous savons que

\(\displaystyle \lim_{n→∞}\dfrac{|x|^{n+1}}{(n+1)!}=0\)

pour n'importe quel nombre réel\(x\). En combinant ce fait avec le théorème de compression, le résultat est\(\displaystyle \lim_{n→∞}R_n(x)=0.\)

b. En utilisant le polynôme de Maclaurin à\(n^{\text{th}}\) -degré\(\sin x\) trouvé dans l'exemple b., nous trouvons que la série de Maclaurin pour\(\sin x\) est donnée par

\(\displaystyle \sum_{n=0}^∞(−1)^n\dfrac{x^{2n+1}}{(2n+1)!}\).

Pour appliquer le test du ratio, considérez

\ [\ begin {align*} \ dfrac {|a_ {n+1} |} {|a_n|} &= \ dfrac {|x|^ {2n+3}} {(2n+3) !} ⋅ \ frac {(2n+1) !} {|x|^ {2n+1}} \ \ [5 points]
&= \ dfrac {|x|^2} {(2n+3) (2n+2)} \ end {align*}. \ aucun numéro \]

Depuis

\(\displaystyle \lim_{n→∞}\dfrac{|x|^2}{(2n+3)(2n+2)}=0\)

pour tous\(x\), nous obtenons l'intervalle de convergence comme\((−∞,∞).\) pour montrer que la série de Maclaurin converge vers\(\sin x\), regardez\(R_n(x)\). Pour chacun,\(x\) il existe un nombre réel\(c\) compris entre\(0\) et\(x\) tel que

\(R_n(x)=\dfrac{f^{(n+1)}(c)}{(n+1)!}x^{n+1}\).

Puisque\(∣f^{(n+1)}(c)∣≤1\) pour tous les entiers\(n\) et tous les nombres réels \(c\), nous avons

\(|R_n(x)|≤\dfrac{|x|^{n+1}}{(n+1)!}\)

pour tous les nombres réels\(x\). En utilisant la même idée que dans la partie a., le résultat est\(\displaystyle \lim_{n→∞}R_n(x)=0\) pour tous et\(x\), par conséquent, la série Maclaurin pour\(\sin x\) converge vers\(\sin x\) tout réel\(x\).

Exercice\(\PageIndex{6}\)

Trouvez la série Maclaurin pour\(f(x)=\cos x\). Utilisez le test du ratio pour montrer que l'intervalle de convergence est de\((−∞,∞)\). Montrez que la série de Maclaurin converge vers tous\(\cos x\) les nombres réels\(x\).

Allusion

Utilisez les polynômes de Maclaurin pour\(\cos x.\)

Réponse

\(\displaystyle \sum_{n=0}^∞\dfrac{(−1)^nx^{2n}}{(2n)!}\)

Selon le test du ratio, l'intervalle de convergence est\((−∞,∞).\) Puisque\(|R_n(x)|≤\dfrac{|x|^{n+1}}{(n+1)!}\), la série converge vers\(\cos x\) pour tous les réels\(x\).

Prouver que\(e\) is Irrational

Dans ce projet, nous utilisons les polynômes de Maclaurin\(e^x\) pour prouver que\(e\) c'est irrationnel. La preuve repose sur le fait de supposer que\(e\) c'est rationnel et d'en arriver à une contradiction. Par conséquent, dans les étapes suivantes, nous supposons que\(e=r/s\) pour certains entiers\(r\) et\(s\) où\(s≠0.\)

1. Écrivez les polynômes de Maclaurin\(p_0(x),p_1(x),p_2(x),p_3(x),p_4(x)\) pour\(e^x\). Évaluer\(p_0(1),p_1(1),p_2(1),p_3(1),p_4(1)\) pour estimer\(e\).
2. \(R_n(x)\)Désignons le reste lorsque vous l'utilisez\(p_n(x)\) pour estimer\(e^x\). Par conséquent\(R_n(x)=e^x−p_n(x)\), et\(R_n(1)=e−p_n(1)\). En supposant que\(e=\dfrac{r}{s}\) pour les nombres entiers\(r\) et\(s\), évaluez\(R_0(1),R_1(1),R_2(1),R_3(1),R_4(1).\)
3. En utilisant les résultats de la partie 2, montrez que pour chaque reste,\(R_0(1),R_1(1),R_2(1),R_3(1),R_4(1),\) nous pouvons trouver un entier\(k\) tel\(kR_n(1)\) qu'un entier pour\(n=0,1,2,3,4.\)
4. Notez la formule du polynôme de Maclaurin à\(n^{\text{th}}\) -degré\(p_n(x)\) pour\(e^x\) et le reste correspondant\(R_n(x).\) Afficher qu'il\(sn!R_n(1)\) s'agit d'un entier.
5. Utilisez le théorème de Taylor pour écrire une formule explicite pour\(R_n(1)\). Concluez que\(R_n(1)≠0\), et donc,\(sn!R_n(1)≠0\).
6. Utilisez le théorème de Taylor pour trouver une estimation sur\(R_n(1)\). Utilisez cette estimation combinée au résultat de la partie 5 pour le montrer\(|sn!R_n(1)|<\dfrac{se}{n+1}\). Concluez qu'il\(n\) est assez grand, alors\(|sn!R_n(1)|<1\). Par conséquent,\(sn!R_n(1)\) est un entier dont l'amplitude est inférieure à 1. Ainsi,\(sn!R_n(1)=0\). Mais à partir de la cinquième partie, nous le savons\(sn!R_n(1)≠0\). Nous sommes arrivés à une contradiction et, par conséquent, la supposition initiale selon laquelle e est rationnel doit être fausse.

Concepts clés

• Les polynômes de Taylor sont utilisés pour approximer des fonctions proches d'une valeur\(x=a\). Les polynômes de Maclaurin sont des polynômes de Taylor à\(x=0\).
• Les polynômes de Taylor à\(n^{\text{th}}\) -degrés pour une fonction\(f\) sont les sommes partielles de la série de Taylor pour\(f\).
• Si une fonction\(f\) possède une représentation de série de puissances à\(x=a\), elle est donnée par sa série de Taylor à\(x=a\).
• Une série Taylor pour\(f\) converge vers\(f\) si et seulement si\(\displaystyle \lim_{n→∞}R_n(x)=0\) où\(R_n(x)=f(x)−p_n(x)\).
• Les séries Taylor pour\(e^x, \sin x\) et\(\cos x\) convergent vers les fonctions respectives pour tous les x réels.

Équations clés

• Série Taylor pour la fonction\(f\) au point\(x=a\)

\(\displaystyle \sum_{n=0}^∞\dfrac{f^{(n)}(a)}{n!}(x−a)^n=f(a)+f′(a)(x−a)+\dfrac{f''(a)}{2!}(x−a)^2+⋯+\dfrac{f^{(n)}(a)}{n!}(x−a)^n+⋯\)

Lexique

Polynôme de Maclaurin

un polynôme de Taylor centré sur\(0\) ; le polynôme de Taylor à\(n^{\text{th}}\) -degré pour\(f\) at\(0\) est le polynôme de Maclaurin à\(n^{\text{th}}\) -degré pour\(f\)

Série Maclaurin

une série Taylor pour une fonction\(f\) à\(x=0\) est connue sous le nom de série Maclaurin pour\(f\)

Polynômes de Taylor

le\(n^{\text{th}}\) polynôme de Taylor à -degrés pour\(f\) at\(x=a\) est\(p_n(x)=f(a)+f′(a)(x−a)+\dfrac{f''(a)}{2!}(x−a)^2+⋯+\dfrac{f^{(n)}(a)}{n!}(x−a)^n\)

Série Taylor

une série de puissances à\(a\) qui converge vers une fonction\(f\) sur un intervalle ouvert contenant\(a\).

Théorème de Taylor avec reste

pour une fonction\(f\) et le polynôme de Taylor à\(n^{\text{th}}\) -degré pour\(f\) at\(x=a\), le reste\(R_n(x)=f(x)−p_n(x)\) satisfait\(R_n(x)=\dfrac{f^{(n+1)}(c)}{(n+1)!}(x−a)^{n+1}\)

pour certains\(c\) entre\(x\) et\(a\) ; s'il existe un intervalle\(I\) contenant\(a\) et un nombre réel\(M\) tel que\(∣f^{(n+1)}(x)∣≤M\) pour tous\(x\) dedans\(I\), alors\(|R_n(x)|≤\dfrac{M}{(n+1)!}|x−a|^{n+1}\)