Skip to main content
Global

10.2E : Exercices pour la section 10.2

  1. Last updated
  2. Save as PDF
  • Page ID
    197107

    • Edwin “Jed” Herman & Gilbert Strang
    • OpenStax
    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    1) Si\(\displaystyle f(x)=\sum_{n=0}^∞\frac{x^n}{n!}\) et\(\displaystyle g(x)=\sum_{n=0}^∞(−1)^n\frac{x^n}{n!}\), trouvez la série de puissance de\(\frac{1}{2}\big(f(x)+g(x)\big)\) et de\(\frac{1}{2}\big(f(x)−g(x)\big)\).

    Réponse
    \(\displaystyle \frac{1}{2}\big(f(x)+g(x)\big)=\sum_{n=0}^∞\frac{x^{2n}}{(2n)!}\)et\(\displaystyle \frac{1}{2}\big(f(x)−g(x)\big)=\sum_{n=0}^∞\frac{x^{2n+1}}{(2n+1)!}\).

    2) Si\(\displaystyle C(x)=\sum_{n=0}^∞\frac{x^{2n}}{(2n)!}\) et\(\displaystyle S(x)=\sum_{n=0}^∞\frac{x^{2n+1}}{(2n+1)!}\), trouvez la série de puissance de\(C(x)+S(x)\) et de\(C(x)−S(x)\).

    Dans les exercices 3 à 6, utilisez des fractions partielles pour déterminer la série de puissances de chaque fonction.

    3)\(\dfrac{4}{(x−3)(x+1)}\)

    Réponse
    \(\displaystyle \frac{4}{(x−3)(x+1)}=\frac{1}{x−3}−\frac{1}{x+1}=−\frac{1}{3(1−\frac{x}{3})}−\frac{1}{1−(−x)}=−\frac{1}{3}\sum_{n=0}^∞\left(\frac{x}{3}\right)^n−\sum_{n=0}^∞(−1)^nx^n=\sum_{n=0}^∞\left((−1)^{n+1}−\frac{1}{3n+1}\right)x^n\)

    4)\(\dfrac{3}{(x+2)(x−1)}\)

    5)\(\dfrac{5}{(x^2+4)(x^2−1)}\)

    Réponse
    \(\displaystyle \frac{5}{(x^2+4)(x^2−1)}=\frac{1}{x^2−1}−\frac{1}{4}\frac{1}{1+\left(\frac{x}{2}\right)^2}=−\sum_{n=0}^∞x^{2n}−\frac{1}{4}\sum_{n=0}^∞(−1)^n\left(\frac{x}{2}\right)^n=\sum_{n=0}^∞\left((−1)+(−1)^{n+1}\frac{1}{2^{n+2}}\right)x^{2n}\)

    6)\(\dfrac{30}{(x^2+1)(x^2−9)}\)

    Dans les exercices 7 à 10, exprimez chaque série comme une fonction rationnelle.

    7)\(\displaystyle \sum_{n=1}^∞\frac{1}{x^n}\)

    Réponse
    \(\displaystyle \frac{1}{x}\sum_{n=0}^∞\frac{1}{x^n}=\frac{1}{x}\cdot \frac{1}{1−\frac{1}{x}}=\frac{1}{x−1}\)

    8)\(\displaystyle \sum_{n=1}^∞\frac{1}{x^{2n}}\)

    9)\(\displaystyle \sum_{n=1}^∞\frac{1}{(x−3)^{2n−1}}\)

    Réponse
    \(\displaystyle \frac{1}{x−3}\cdot \frac{1}{1−\frac{1}{(x−3)^2}}=\frac{x−3}{(x−3)^2−1}\)

    10)\(\displaystyle \sum_{n=1}^∞\left(\frac{1}{(x−3)^{2n−1}}−\frac{1}{(x−2)^{2n−1}}\right)\)

    Les exercices 11 à 16 explorent les applications des rentes.

    11) Calculez les valeurs actuelles\(P\) d'une rente dans laquelle 10 000 dollars doivent être versés chaque année pendant une période de 20 ans, en supposant des taux d'intérêt de\(r=0.03,\, r=0.05\), et\(r=0.07\).

    Réponse
    \(P=P_1+⋯+P_{20}\)où\(P_k=10,000\dfrac{1}{(1+r)^k}\). Alors\(\displaystyle P=10,000\sum_{k=1}^{20}\frac{1}{(1+r)^k}=10,000\frac{1−(1+r)^{−20}}{r}\). Quand,\(r=0.03, \,P≈10,000×14.8775=148,775.\) quand,\(r=0.05, \,P≈10,000×12.4622=124,622.\) quand\(r=0.07, \, P≈105,940\).

    12) Calculez les valeurs actuelles\(P\) des rentes dans lesquelles 9 000 dollars doivent être versés chaque année de façon perpétuelle, en supposant des taux d'intérêt de\(r=0.03,\, r=0.05\) et\(r=0.07\).

    13) Calculez les versements annuels\(C\) à verser pendant 20 ans sur des rentes d'une valeur actuelle de 100 000 dollars en supposant des taux d'intérêt respectifs de\(r=0.03,\, r=0.05,\) et\(r=0.07.\)

    Réponse
    En général,\(P=\dfrac{C(1−(1+r)^{−N})}{r}\) pour des\(N\) années de paiements, ou\(C=\dfrac{Pr}{1−(1+r)^{−N}}\). Car\(N=20\) et\(P=100,000\),\(C=6721.57\) on a\(r=0.03; \, C=8024.26\) quand\(r=0.05\), et\(C≈9439.29\) quand\(r=0.07\).

    14) Calculez les versements annuels\(C\) à verser perpétuellement sur les rentes d'une valeur actuelle de 100 000 dollars en supposant des taux d'intérêt respectifs de\(r=0.03, \,r=0.05,\) et\(r=0.07\).

    15) Supposons qu'une rente ait une valeur actualisée de\(P=1\) millions de dollars. Quel taux d'intérêt\(r\) permettrait des versements annuels perpétuels de 50 000$ ?

    Réponse
    D'une manière générale,\(P=\dfrac{C}{r}.\) Ainsi,\(r=\dfrac{C}{P}=5×\frac{10^4}{10^6}=0.05.\)

    16) Supposons qu'une rente ait une valeur actualisée de\(P=10\) millions de dollars. Quel taux d'intérêt\(r\) permettrait des versements annuels perpétuels de 100 000$ ?

    Dans les exercices 17 à 20, exprimez la somme de chaque série de puissance en termes de séries géométriques, puis exprimez la somme sous forme de fonction rationnelle.

    17)\(x+x^2−x^3+x^4+x^5−x^6+⋯\) (Indice : pouvoirs du groupe\(x^{3k}, \, x^{3k−1},\) et\(x^{3k−2}\).)

    Réponse
    \((x+x^2−x^3)(1+x^3+x^6+⋯)=\dfrac{x+x^2−x^3}{1−x^3}\)

    18)\(x+x^2−x^3−x^4+x^5+x^6−x^7−x^8+⋯\) (Indice : pouvoirs du groupe\(x^{4k}, \, x^{4k−1},\), etc.)

    19)\(x−x^2−x^3+x^4−x^5−x^6+x^7−⋯\) (Indice : pouvoirs du groupe\(x^{3k}, \, x^{3k−1}\), et\(x^{3k−2}\).)

    Réponse
    \((x−x^2−x^3)(1+x^3+x^6+⋯)=\dfrac{x−x^2−x^3}{1−x^3}\)

    20)\(\displaystyle \frac{x}{2}+\frac{x^2}{4}−\frac{x^3}{8}+\frac{x^4}{16}+\frac{x^5}{32}−\frac{x^6}{64}+⋯\) (Indice : pouvoirs du groupe\(\left(\dfrac{x}{2}\right)^{3k}, \, \left(\dfrac{x}{2}\right)^{3k−1},\) et\(\left(\dfrac{x}{2}\right)^{3k−2}\).)

    Dans les exercices 21 à 24, trouvez la série de puissance\(f(x)g(x)\) donnée\(f\) et telle\(g\) que définie.

    (21)\(\displaystyle f(x)=2\sum_{n=0}^∞x^n,g(x)=\sum_{n=0}^∞nx^n\)

    Réponse
    \(a_n=2, \, b_n=n\)donc\(\displaystyle c_n=\sum_{k=0}^nb_ka_{n−k}=2\sum_{k=0}^nk=(n)(n+1)\) et\(\displaystyle f(x)g(x)=\sum_{n=1}^∞n(n+1)x^n\)

    22)\(\displaystyle f(x)=\sum_{n=1}^∞x^n,\; g(x)=\sum_{n=1}^∞\frac{1}{n}x^n\). Exprimez les coefficients de\(f(x)g(x)\) en termes de\(\displaystyle H_n=\sum_{k=1}^n\frac{1}{k}\).

    23)\(\displaystyle f(x)=g(x)=\sum_{n=1}^∞\left(\frac{x}{2}\right)^n\)

    Réponse
    \(a_n=b_n=2^{−n}\)donc\(\displaystyle c_n=\sum_{k=1}^nb_ka_{n−k}=2^{−n}\sum_{k=1}^n1=\frac{n}{2^n}\) et\(\displaystyle f(x)g(x)=\sum_{n=1}^∞n\left(\frac{x}{2}\right)^n\)

    (24)\(\displaystyle f(x)=g(x)=\sum_{n=1}^∞nx^n\)

    Dans les exercices 25 à 26, différenciez l'expansion de série donnée\(f\) terme par terme pour obtenir l'expansion de série correspondante pour la dérivée de\(f.\)

    25)\(\displaystyle f(x)=\frac{1}{1+x}=\sum_{n=0}^∞(−1)^nx^n\)

    Réponse
    Le dérivé de\(f\) est\(\displaystyle −\frac{1}{(1+x)^2}=−\sum_{n=0}^∞(−1)^n(n+1)x^n\).

    (26)\(\displaystyle f(x)=\frac{1}{1−x^2}=\sum_{n=0}^∞x^{2n}\)

    Dans les exercices 27 à 28, intégrez l'expansion de série donnée\(f\) terme par terme à partir de zéro\(x\) pour obtenir l'expansion de série correspondante pour l'intégrale indéfinie de\(f\).

    (27)\(\displaystyle f(x)=\frac{2x}{(1+x^2)^2}=\sum_{n=1}^∞(−1)^n(2n)x^{2n−1}\)

    Réponse
    L'intégrale indéfinie de\(f\) est\(\displaystyle \frac{1}{1+x^2}=\sum_{n=0}^∞(−1)^nx^{2n}\).

    (28)\(\displaystyle f(x)=\frac{2x}{1+x^2}=2\sum_{n=0}^∞(−1)^nx^{2n+1}\)

    Dans les exercices 29 à 32, évaluez chaque série infinie en l'identifiant comme la valeur d'une dérivée ou d'une intégrale de séries géométriques.

    29) Évaluez\(\displaystyle \sum_{n=1}^∞\frac{n}{2^n}\) comme\(f′\left(\frac{1}{2}\right)\) où\(\displaystyle f(x)=\sum_{n=0}^∞x^n\).

    Réponse
    \(\displaystyle f(x)=\sum_{n=0}^∞x^n=\frac{1}{1−x}; \; f′(\frac{1}{2})=\sum_{n=1}^∞\frac{n}{2^{n−1}}=\frac{d}{dx}(1−x)^{−1}\Big|_{x=1/2}=\frac{1}{(1−x)^2}\Big|_{x=1/2}=4\)donc\(\displaystyle \sum_{n=1}^∞\frac{n}{2^n}=2.\)

    30) Évaluez\(\displaystyle \sum_{n=1}^∞\frac{n}{3^n}\) comme\(f′\left(\frac{1}{3}\right)\) où\(\displaystyle f(x)=\sum_{n=0}^∞x^{6n}\).

    31) Évaluez\(\displaystyle \sum_{n=2}^∞\frac{n(n−1)}{2^n}\) comme\(f''\left(\frac{1}{2}\right)\) où\(\displaystyle f(x)=\sum_{n=0}^∞x^n\).

    Réponse
    \(\displaystyle f(x)=\sum_{n=0}^∞x^n=\frac{1}{1−x}; \; f''\left(\frac{1}{2}\right)=\sum_{n=2}^∞\frac{n(n−1)}{2^{n−2}}=\frac{d^2}{dx^2}(1−x)^{−1}\Big|_{x=1/2}=\frac{2}{(1−x)^3}\Big|_{x=1/2}=16\)donc\(\displaystyle \sum_{n=2}^∞n\frac{(n−1)}{2^n}=4.\)

    32) Évaluez\(\displaystyle \sum_{n=0}^∞\frac{(−1)^n}{n+1}\) comme\(\displaystyle ∫^1_0f(t) \, dt\) où\(\displaystyle f(x)=\sum_{n=0}^∞(−1)^nx^{2n}=\frac{1}{1+x^2}\).

    Dans les exercices 33 à 39, étant donné cela\(\displaystyle \frac{1}{1−x}=\sum_{n=0}^∞x^n\), utilisez la différenciation ou l'intégration terme par terme pour trouver des séries de puissance pour chaque fonction centrée sur le point donné.

    33)\(f(x)=\ln x\) centré sur\(x=1\) (Astuce :\(x=1−(1−x)\))

    Réponse
    \(\displaystyle ∫\sum(1−x)^n\,dx=∫\sum(−1)^n(x−1)^n\,dx=\sum \frac{(−1)^n(x−1)^{n+1}}{n+1}\)

    34)\(\ln(1−x)\) à\(x=0\)

    35)\(\ln(1−x^2)\) à\(x=0\)

    Réponse
    \(\displaystyle −∫^{x^2}_{t=0}\frac{1}{1−t}dt=−\sum_{n=0}^∞∫^{x^2}_0t^ndx−\sum_{n=0}^∞\frac{x^{2(n+1)}}{n+1}=−\sum_{n=1}^∞\frac{x^{2n}}{n}\)

    36)\(f(x)=\dfrac{2x}{(1−x^2)^2}\) à\(x=0\)

    37)\(f(x)=\tan^{−1}(x^2)\) à\(x=0\)

    Réponse
    \(\displaystyle ∫^{x^2}_0\frac{dt}{1+t^2}=\sum_{n=0}^∞(−1)^n∫^{x^2}_0t^{2n}dt=\sum_{n=0}^∞(−1)^n\frac{t^{2n+1}}{2n+1}∣^{x^2}_{t=0}=\sum_{n=0}^∞(−1)^n\frac{x^{4n+2}}{2n+1}\)

    38)\(f(x)=\ln(1+x^2)\) à\(x=0\)

    39)\(\displaystyle f(x)=∫^x_0\ln t\,dt\) où\(\displaystyle \ln(x)=\sum_{n=1}^∞(−1)^{n−1}\frac{(x−1)^n}{n}\)

    Réponse
    L'intégration terme par trimestre donne\(\displaystyle ∫^x_0\ln t\,dt=\sum_{n=1}^∞(−1)^{n−1}\frac{(x−1)^{n+1}}{n(n+1)}=\sum_{n=1}^∞(−1)^{n−1}\left(\frac{1}{n}−\frac{1}{n+1}\right)(x−1)^{n+1}=(x−1)\ln x+\sum_{n=2}^∞(−1)^n\frac{(x−1)^n}{n}=x\ln x−x.\)

    40) [T] Évaluez l'expansion de la série de puissance\(\displaystyle \ln(1+x)=\sum_{n=1}^∞(−1)^{n−1}\frac{x^n}{n}\)\(x=1\) à pour montrer qu'il\(\ln(2)\) s'agit de la somme des séries harmoniques alternées. Utilisez le test des séries alternées pour déterminer le nombre de termes de la somme nécessaires pour effectuer une estimation\(\ln(2)\) précise\(0.001,\) et trouver une telle approximation.

    41) [T] Soustrayez la série infinie\(\ln(1−x)\) de\(\ln(1+x)\) pour obtenir une série de puissance pour\(\ln\left(\dfrac{1+x}{1−x}\right)\). Évaluez à\(x=\frac{1}{3}\). Quelle est la plus petite de\(N\) telle sorte que la somme\(N^{\text{th}}\) partielle de cette série se rapproche\(\ln(2)\) avec une erreur inférieure à\(0.001\) ?

    Réponse
    Nous l'avons\(\displaystyle \ln(1−x)=−\sum_{n=1}^∞\frac{x^n}{n}\) fait\(\displaystyle \ln(1+x)=\sum_{n=1}^∞(−1)^{n−1}\frac{x^n}{n}\). Ainsi,\(\displaystyle \ln\left(\frac{1+x}{1−x}\right)=\sum_{n=1}^∞\big(1+(−1)^{n−1}\big)\frac{x^n}{n}=2\sum_{n=1}^∞\frac{x^{2n−1}}{2n−1}\). Quand\(x=\frac{1}{3}\) nous obtenons\(\displaystyle \ln(2)=2\sum_{n=1}^∞\frac{1}{3^{2n−1}(2n−1)}\). Nous avons\(\displaystyle 2\sum_{n=1}^3\frac{1}{3^{2n−1}(2n−1)}=0.69300…\), pendant\(\displaystyle 2\sum_{n=1}^4\frac{1}{3^{2n−1}(2n−1)}=0.69313…\) et\(\ln(2)=0.69314…;\) donc,\(N=4\).

    Dans les exercices 42 à 45, en utilisant une substitution si elle est indiquée, exprimez chaque série en termes de fonctions élémentaires et trouvez le rayon de convergence de la somme.

    (42)\(\displaystyle \sum_{k=0}^∞(x^k−x^{2k+1})\)

    43)\(\displaystyle \sum_{k=1}^∞\frac{x^{3k}}{6k}\)

    Réponse
    \(\displaystyle \sum_{k=1}^∞\frac{x^k}{k}=−\ln(1−x)\)donc\(\displaystyle \sum_{k=1}^∞\frac{x^{3k}}{6k}=−\frac{1}{6}\ln(1−x^3)\). Le rayon de convergence est égal\(1\) par le test du ratio.

    44)\(\displaystyle \sum_{k=1}^∞(1+x^2)^{−k}\) en utilisant\(y=\dfrac{1}{1+x^2}\)

    45)\(\displaystyle \sum_{k=1}^∞2^{−kx}\) en utilisant\(y=2^{−x}\)

    Réponse
    Si\(y=2^{−x}\), alors\(\displaystyle \sum_{k=1}^∞y^k=\frac{y}{1−y}=\frac{2^{−x}}{1−2^{−x}}=\frac{1}{2^x−1}\). Si\(a_k=2^{−kx}\), alors\(\dfrac{a_{k+1}}{a_k}=2^{−x}<1\) quand\(x>0\). La série converge donc pour tous\(x>0\).

    46) Montrez que, jusqu'aux pouvoirs\(x^3\) et\(y^3\),\(\displaystyle E(x)=\sum_{n=0}^∞\frac{x^n}{n!}\) satisfait\(E(x+y)=E(x)E(y)\).

    47) Différenciez la série\(\displaystyle E(x)=\sum_{n=0}^∞\frac{x^n}{n!}\) terme par terme pour montrer qu'elle\(E(x)\) est égale à sa dérivée.

    Réponse
    Les réponses peuvent varier.

    48) Montrez que si\(\displaystyle f(x)=\sum_{n=0}^∞a_nx^n\) c'est une somme de puissances paires, c'est-à-dire que\(a_n=0\) si elle\(n\) est impaire, alors\(\displaystyle F=∫^x_0f(t)\, dt\) est une somme de puissances impaires, alors que si\(I\) c'est une somme de puissances impaires, alors\(F\) est une somme de puissances paires.

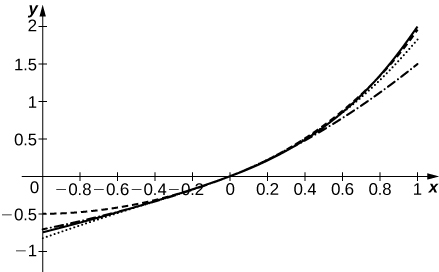
    49) [T] Supposons que les coefficients an de la série\(\displaystyle \sum_{n=0}^∞a_nx^n\) soient définis par la relation de récurrence\(a_n=\dfrac{a_{n−1}}{n}+\dfrac{a_{n−2}}{n(n−1)}\). Pour\(a_0=0\) et\(a_1=1\), calculez et tracez les sommes\(\displaystyle S_N=\sum_{n=0}^Na_nx^n\) pour\(N=2,3,4,5\)\([−1,1].\)

    Réponse

    La courbe continue est\(S_5\). La courbe en pointillés est\(S_2\), en pointillés est\(S_3\) et en pointillés est\(S_4\)

    Il s'agit d'un graphique de trois courbes. Elles augmentent toutes et deviennent très proches lorsque les courbes s'approchent de x = 0. Ensuite, ils se séparent lorsque x s'éloigne de 0.

    50) [T] Supposons que les coefficients an de la série\(\displaystyle \sum_{n=0}^∞a_nx^n\) soient définis par la relation de récurrence\(a_n=\dfrac{a_{n−1}}{\sqrt{n}}−\dfrac{a_{n−2}}{\sqrt{n(n−1)}}\). Pour\(a_0=1\) et\(a_1=0\), calculez et tracez les sommes\(\displaystyle S_N=\sum_{n=0}^Na_nx^n\) pour\(N=2,3,4,5\) on\([−1,1]\).

    51) [T] Compte tenu de l'expansion de la série de puissances\(\displaystyle \ln(1+x)=\sum_{n=1}^∞(−1)^{n−1}\frac{x^n}{n}\), déterminez le nombre\(N\) de termes de la somme évaluée à qui\(x=−1/2\) sont nécessaires pour obtenir\(\ln(2)\) une approximation précise de la somme partielle correspondante\(\displaystyle \sum_{n=1}^N(−1)^{n−1}\frac{x^n}{n}\).\(1/1000.\)

    Réponse
    Quand\(\displaystyle x=−\frac{1}{2}, \;−\ln(2)=\ln\left(\frac{1}{2}\right)=−\sum_{n=1}^∞\frac{1}{n2^n}\). Puisque\(\displaystyle \sum^∞_{n=11}\frac{1}{n2^n}<\sum_{n=11}^∞\frac{1}{2^n}=\frac{1}{2^{10}},\) l'on a\(\displaystyle \sum_{n=1}^{10}\frac{1}{n2^n}=0.69306…\),\(\ln(2)=0.69314…;\) par conséquent,\(N=10.\)

    52) [T] Compte tenu de l'expansion de la série de puissances\(\displaystyle \tan^{−1}(x)=\sum_{k=0}^∞(−1)^k\frac{x^{2k+1}}{2k+1}\), utilisez le test des séries alternées pour déterminer combien\(N\) de termes de la somme évaluée à\(x=1\) sont nécessaires pour\(\tan^{−1}(1)=\frac{π}{4}\) obtenir une précision approximative avec\(1/1000.\) Evaluer la somme partielle correspondante\(\displaystyle \sum_{k=0}^N(−1)^k\frac{x^{2k+1}}{2k+1}\).

    53) [T] Rappelons qu'\(\tan^{−1}\left(\frac{1}{\sqrt{3}}\right)=\frac{π}{6}.\)en supposant une valeur exacte de\(\frac{1}{\sqrt{3}})\), estimez\(\frac{π}{6}\) en évaluant des sommes partielles\(S_N\left(\frac{1}{\sqrt{3}}\right)\) de l'expansion de la série de puissances\(\displaystyle \tan^{−1}(x)=\sum_{k=0}^∞(−1)^k\frac{x^{2k+1}}{2k+1}\) à\(x=\frac{1}{\sqrt{3}}\). Quel est le plus petit\(N\) nombre qui\(6S_N\left(\frac{1}{\sqrt{3}}\right)\) se rapproche\(π\) exactement de l'intérieur\(0.001\) ? Combien de termes sont nécessaires pour obtenir une précision maximale\(0.00001\) ?

    Réponse
    \(\displaystyle 6S_N\left(\frac{1}{\sqrt{3}}\right)=2\sqrt{3}\sum_{n=0}^N(−1)^n\frac{1}{3^n(2n+1).}\)L'un a\(π−6S_4\left(\frac{1}{\sqrt{3}}\right)=0.00101…\) et\(N=5\) est\(π−6S_5\left(\frac{1}{\sqrt{3}}\right)=0.00028…\) donc la plus petite somme partielle avec précision à l'intérieur\(0.001.\) De même,\(π−6S_7\left(\frac{1}{\sqrt{3}}\right)=0.00002…\) tandis que\(π−6S_8\left(\frac{1}{\sqrt{3}}\right)=−0.000007…\) c'\(N=8\)est la plus petite\(N\) pour donner de la précision à l'intérieur\(0.00001.\)