10.4 : Travailler avec la série Taylor
- Page ID
- 197136
- Écrivez les termes de la série binomiale.
- Reconnaissez les extensions de fonctions courantes de la série Taylor.
- Reconnaissez et appliquez des techniques pour trouver la série Taylor correspondant à une fonction.
- Utilisez les séries de Taylor pour résoudre des équations différentielles.
- Utilisez la série Taylor pour évaluer les intégrales non élémentaires.
Dans la section précédente, nous avons défini les séries de Taylor et montré comment trouver la série de Taylor pour plusieurs fonctions courantes en calculant explicitement les coefficients des polynômes de Taylor. Dans cette section, nous montrons comment utiliser ces séries de Taylor pour dériver des séries de Taylor pour d'autres fonctions. Nous présentons ensuite deux applications courantes des séries électriques. Tout d'abord, nous montrons comment les séries de puissances peuvent être utilisées pour résoudre des équations différentielles. Ensuite, nous montrons comment les séries de puissance peuvent être utilisées pour évaluer des intégrales lorsque l'antidérivée de l'integrand ne peut pas être exprimée en termes de fonctions élémentaires. Dans un exemple, nous considérons\(\displaystyle \int e^{−x^2}dx,\) une intégrale qui apparaît fréquemment dans la théorie des probabilités.
La série Binomial
Notre premier objectif dans cette section est de déterminer la série de Maclaurin pour la fonction\( f(x)=(1+x)^r\) pour tous les nombres réels\( r\). La série de Maclaurin pour cette fonction est connue sous le nom de série binomiale. Nous commençons par considérer le cas le plus simple :\( r\) est un entier non négatif. Nous rappelons que, car\( r=0,\,1,\,2,\,3,\,4,\;f(x)=(1+x)^r\) peut s'écrire
\[\begin{align*} f(x) &=(1+x)^0=1, \\[4pt] f(x) &=(1+x)^1=1+x, \\[4pt] f(x) &=(1+x)^2=1+2x+x^2, \\[4pt] f(x) &=(1+x)^3=1+3x+3x^2+x^3 \\[4pt] f(x) &=(1+x)^4=1+4x+6x^2+4x^3+x^4. \end{align*}\]
Les expressions du côté droit sont appelées expansions binomiales et les coefficients sont appelés coefficients binomiaux. Plus généralement, pour tout entier non négatif\( r\), le coefficient binomial de\( x^n\) dans l'expansion binomiale de\( (1+x)^r\) est donné par
\[\binom{r}{n}=\dfrac{r!}{n!(r−n)!}\label{eq6.6} \]
et
\ [\ begin {align} f (x) &= (1+x) ^r \ nonumber \ \ [5 points]
&= \ binom {r} {0} + \ binom {r} {1} x+ \ binom {r} {2} x^2+ \ binom {r} {3} x^3++ \ binom {r} {r-1} x^ {r−1} + \ binom {r} {r} x^r \ nonumber \ \ [5 points]
&= \ sum_ {n=0} ^r \ binom {r} {n} x^n. \ label {eq6.7} \ end {align} \]
Par exemple, en utilisant cette formule pour\( r=5\), nous voyons que
\[ \begin{align*} f(x) &=(1+x)^5 \\[4pt] &=\binom{5}{0}1+\binom{5}{1}x+\binom{5}{2}x^2+\binom{5}{3}x^3+\binom{5}{4}x^4+\binom{5}{5}x^5 \\[4pt] &=\dfrac{5!}{0!5!}1+\dfrac{5!}{1!4!}x+\dfrac{5!}{2!3!}x^2+\dfrac{5!}{3!2!}x^3+\dfrac{5!}{4!1!}x^4+\dfrac{5!}{5!0!}x^5 \\[4pt] &=1+5x+10x^2+10x^3+5x^4+x^5. \end{align*}\]
Nous considérons maintenant le cas où l'exposant\(r.\)
est un nombre réel, pas nécessairement un entier non négatif. Si\(r\) ce n'est pas un entier non négatif, il\(f(x)=(1+x)^r\) ne peut pas être écrit comme un polynôme fini. Cependant, nous pouvons trouver une série de puissance pour\(f\). Plus précisément, nous recherchons la série Maclaurin pour\(f\). Pour ce faire, nous trouvons les dérivées de\(f\) et les évaluons à\(x=0\).
\[ \begin{align*} f(x) &=(1+x)^r & f(0) &=1 \\[4pt] f′(x) &=r(1+x)^{r−1} & f'(0) &=r \\[4pt] f''(x) &=r(r−1)(1+x)^{r−2} & f''(0) &=r(r−1) \\[4pt] f'''(x) &=r(r−1)(r−2)(1+x)^{r−3} & f'''(0) &=r(r−1)(r−2) \\[4pt] f^{(n)}(x) &=r(r−1)(r−2)⋯(r−n+1)(1+x)^{r−n} & f^{(n)}(0) &=r(r−1)(r−2)⋯(r−n+1) \end{align*}\]
Nous concluons que les coefficients des séries binomiales sont donnés par
\[\dfrac{f^{(n)}(0)}{n!}=\dfrac{r(r−1)(r−2)⋯(r−n+1)}{n!}.\label{eq6.8} \]
Nous notons que si\(r\) est un entier non négatif, alors la\((r+1)^{\text{st}}\) dérivée\( f^{(r+1)}\) est la fonction zéro et la série se termine. De plus, s'il s'\( r\)agit d'un entier non négatif, alors l'équation \ ref {eq6.8} pour les coefficients correspond à l'équation \ ref {eq6.6} pour les coefficients, et la formule pour la série binomiale correspond à l'équation \ ref {eq6.7} pour l'expansion binomiale finie. Plus généralement, pour désigner les coefficients binomiaux pour tout nombre réel\( r\), nous définissons
\[\binom{r}{n}=\dfrac{(r−1)(r−2)⋯(r−n+1)}{n!}. \nonumber \]
Avec cette notation, nous pouvons écrire la série binomiale pour\( (1+x)^r\) as
\[\sum_{n=0}^∞\binom{r}{n}x^n=1+rx+\dfrac{r(r−1)}{2!}x^2+⋯+\dfrac{r(r−1)⋯(r−n+1)}{n!}x^n+⋯. \label{bin1} \]
Nous devons maintenant déterminer l'intervalle de convergence pour la série binomiale Equation \ ref {bin1}. Nous appliquons le test du ratio. Par conséquent, nous considérons
\[\begin{align*} \dfrac{|a_{n+1}|}{|a_n|} &=\dfrac{|r(r−1)(r−2)⋯(r−n)|x||^{n+1}}{(n+1)!}⋅\dfrac{n}{|r(r−1)(r−2)⋯(r−n+1)||x|^n} \\[4pt] &=\dfrac{|r−n||x|}{|n+1|} \end{align*}\].
Depuis
\[\lim_{n→∞}\dfrac{|a_{n+1}|}{|a_n|}=|x|<1 \nonumber \]
si et seulement si\( |x|<1\), nous concluons que l'intervalle de convergence pour la série binomiale est\( (−1,1)\). Le comportement aux points de terminaison dépend de\( r\). On peut montrer que pour\( r≥0\) la série converge aux deux extrémités ; pour\( −1<r<0\), la série converge vers\( x=1\) et diverge vers\( x=−1\) ; et pour\( r<−1\), pour, la série diverge aux deux extrémités. La série binomiale converge vers\( (1+x)^r\) in\( (−1,1)\) pour tous les nombres réels\( r\), mais prouver ce fait en montrant que le reste\( R_n(x)→0\) est difficile.
Pour tout nombre réel\( r\), la série de Maclaurin pour\( f(x)=(1+x)^r\) est la série binomiale. Il converge vers\( f\) pour\( |x|<1\), et nous écrivons
\[(1+x)^r=\sum_{n=0}^∞\binom{r}{n}x^n=1+rx+\dfrac{r(r−1)}{2!}x^2+⋯+r\dfrac{(r−1)⋯(r−n+1)}{n!}x^n+⋯ \nonumber \]
pour\( |x|<1\).
Nous pouvons utiliser cette définition pour trouver la série binomiale pour\( f(x)=\sqrt{1+x}\) et utiliser la série à des fins approximatives\( \sqrt{1.5}\).
- Trouvez la série binomiale pour\( f(x)=\sqrt{1+x}\).
- Utilisez le polynôme de Maclaurin du troisième ordre\( p_3(x)\) pour effectuer une estimation\( \sqrt{1.5}\). Utilisez le théorème de Taylor pour limiter l'erreur. Utilisez un utilitaire de création de graphiques pour comparer les graphes de\( f\) et\( p_3\).
Solution
a. Ici\( r=\dfrac{1}{2}\). En utilisant la définition de la série binomiale, nous obtenons
\ (\ displaystyle \ qquad \ begin {align*} \ sqrt {1+x} &=1+ \ dfrac {1} {2} x+ \ dfrac {(1/2) (−1/2)} {2 !} x^2+ \ dfrac {(1/2) (−1/2) (−3/2)} {3 !} x^3+\ \ [5 points]
&=1+ \ dfrac {1} {2} x− \ dfrac {1} {2 !} \ dfrac {1} {2^2} x^2+ \ dfrac {1} {3 !} \ dfrac {1⋅3} {2^3} x^3−+ \ dfrac {(−1) ^ {n+1}} {n !} \ dfrac {1⋅3⋅5 (2n−3)} {2^n} x^n+\ \ [5 points]
&=1+ \ sum_ {n=1} ^∞ \ dfrac {(−1) ^ {n+1}} {n !} \ dfrac {1⋅3⋅5 (2n−3)} {2^n} x^n. \ end {align*} \)
b. D'après le résultat de la partie a., le polynôme de Maclaurin du troisième ordre est
\( p_3(x)=1+\dfrac{1}{2}x−\dfrac{1}{8}x^2+\dfrac{1}{16}x^3\).
Par conséquent,
\( \sqrt{1.5}=\sqrt{1+0.5}≈1+\dfrac{1}{2}(0.5)−\dfrac{1}{8}(0.5)^2+\dfrac{1}{16}(0.5)^3≈1.2266.\)
D'après le théorème de Taylor, l'erreur satisfait
\( R_3(0.5)=\dfrac{f^{(4)}(c)}{4!}(0.5)^4\)
pour certains\( c\) entre\( 0\) et\( 0.5\). Puisque\( f^{(4)}(x)=−\dfrac{15}{2^4(1+x)^{7/2}}\), et que la valeur maximale de\( ∣f^{(4)}(x)∣\) l'intervalle\( (0,0.5)\) se produit à\( x=0\), nous avons
\( |R_3(0.5)|≤\dfrac{15}{4!2^4}(0.5)^4≈0.00244.\)
La fonction et le polynôme de Maclaurin\( p_3\) sont représentés sur la figure\(\PageIndex{1}\).
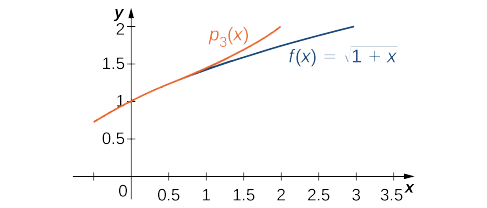
Trouvez la série binomiale pour\( f(x)=\dfrac{1}{(1+x)^2}\).
- Allusion
-
Utilisez la définition des séries binomiales pour\( r=−2\).
- Réponse
-
\(\displaystyle \sum_{n=0}^∞(−1)^n(n+1)x^n\)
Fonctions communes exprimées sous forme de séries Taylor
À ce stade, nous avons dérivé des séries de Maclaurin pour les fonctions exponentielles, trigonométriques et logarithmiques, ainsi que pour les fonctions de la forme\( f(x)=(1+x)^r\). Dans le tableau\(\PageIndex{1}\), nous résumons les résultats de ces séries. Nous remarquons que la convergence de la série de Maclaurin pour l'\( f(x)=\ln(1+x)\)extrémité\( x=1\) et de la série de Maclaurin pour les\( f(x)=\tan^{−1}x\) extrémités\( x=1\)\( x=−1\) repose sur un théorème plus avancé que celui que nous présentons ici. (Reportez-vous au théorème d'Abel pour une discussion sur ce point plus technique.)
| Fonction | Série Maclaurin | Intervalle de convergence |
|---|---|---|
| \( f(x)=\dfrac{1}{1−x}\) | \(\displaystyle \sum_{n=0}^∞x^n\) | \( −1<x<1\) |
| \( f(x)=e^x\) | \(\displaystyle \sum_{n=0}^∞\dfrac{x^n}{n!}\) | \( −∞<x<∞\) |
| \( f(x)=\sin x\) | \(\displaystyle \sum_{n=0}^∞(−1)^n\dfrac{x^{2n+1}}{(2n+1)!}\) | \( −∞<x<∞\) |
| \( f(x)=\cos x\) | \(\displaystyle \sum_{n=0}^∞(−1)^n\dfrac{x^{2n}}{(2n)!}\) | \( −∞<x<∞\) |
| \( f(x)=\ln(1+x)\) | \(\displaystyle \sum_{n=0}^∞(−1)^{n+1}\dfrac{x^n}{n}\) | \( −1<x<1\) |
| \( f(x)=\tan^{−1}x\) | \(\displaystyle \sum_{n=0}^∞(−1)^n\dfrac{x^{2n+1}}{2n+1}\) | \( −1<x<1\) |
| \( f(x)=(1+x)^r\) | \(\displaystyle \sum_{n=0}^∞\binom{r}{n}x^n\) | \( −1<x<1\) |
Plus tôt dans le chapitre, nous avons montré comment combiner des séries de puissance pour créer de nouvelles séries de puissance. Nous utilisons ici ces propriétés, combinées à la série Maclaurin dans Tableau\(\PageIndex{1}\), pour créer des séries de Maclaurin pour d'autres fonctions.
Trouvez la série Maclaurin de chacune des fonctions suivantes en utilisant l'une des séries répertoriées dans le tableau\(\PageIndex{1}\).
- \( f(x)=\cos\sqrt{x}\)
- \( f(x)=\sinh x\)
Solution
a. En utilisant la série Maclaurin pour,\( \cos x\) nous constatons que la série Maclaurin pour\( \cos\sqrt{x}\) est donnée par
\(\displaystyle \sum_{n=0}^∞\dfrac{(−1)^n(\sqrt{x})^{2n}}{(2n)!}=\sum_{n=0}^∞\dfrac{(−1)^nx^n}{(2n)!}=1−\dfrac{x}{2!}+\dfrac{x^2}{4!}−\dfrac{x^3}{6!}+\dfrac{x^4}{8!}−⋯.\)
Cette série converge vers\( \cos\sqrt{x}\) pour tous\( x\) dans le domaine de\( \cos\sqrt{x}\) ; c'est-à-dire pour tous\( x≥0\).
b. Pour trouver la série Maclaurin,\( \sinh x,\) nous utilisons le fait que
\( \sinh x=\dfrac{e^x−e^{−x}}{2}.\)
En utilisant la série Maclaurin pour\( e^x\), nous voyons que le\(n^{\text{th}}\) terme dans la série Maclaurin pour\(\sinh x\) est donné par
\( \dfrac{x^n}{n!}−\dfrac{(−x)^n}{n!}.\)
Pour\( n\) pair, ce terme est nul. Pour\( n\) étrange, ce terme est\( \dfrac{2x^n}{n!}\). Par conséquent, la série Maclaurin pour ne\(\sinh x\) contient que des termes impairs et est donnée par
\(\displaystyle \sum_{n=0}^∞\dfrac{x^{2n+1}}{(2n+1)!}=x+\dfrac{x^3}{3!}+\dfrac{x^5}{5!}+⋯.\)
Trouvez la série Maclaurin pour\( \sin(x^2).\)
- Allusion
-
Utilisez la série Maclaurin pour\( \sin x.\)
- Réponse
-
\(\displaystyle \sum_{n=0}^∞\dfrac{(−1)^nx^{4n+2}}{(2n+1)!}\)
Nous avons également montré précédemment dans ce chapitre comment les séries de puissance peuvent être différenciées terme par terme pour créer une nouvelle série de puissances. Dans l'exemple\(\PageIndex{3}\), nous différencions les séries binomiales\( \sqrt{1+x}\) terme par terme afin de trouver la série binomiale pour\( \dfrac{1}{\sqrt{1+x}}\). Notez que nous pouvons construire la série binomiale pour\( \dfrac{1}{\sqrt{1+x}}\) directement à partir de la définition, mais la différenciation des séries binomiales pour\( \sqrt{1+x}\) est un calcul plus facile.
Utilisez la série binomiale\( \sqrt{1+x}\) pour trouver la série binomiale pour\( \dfrac{1}{\sqrt{1+x}}\).
Solution
Les deux fonctions sont liées par
\( \dfrac{d}{dx}\sqrt{1+x}=\dfrac{1}{2\sqrt{1+x}}\),
donc la série binomiale pour\( \dfrac{1}{\sqrt{1+x}}\) est donnée par
\(\displaystyle \dfrac{1}{\sqrt{1+x}}=2\dfrac{d}{dx}\sqrt{1+x}=1+\sum_{n=1}^∞\dfrac{(−1)^n}{n!}\dfrac{1⋅3⋅5⋯(2n−1)}{2^n}x^n.\)
Trouvez la série binomiale pour\( f(x)=\dfrac{1}{(1+x)^{3/2}}\)
- Allusion
-
Différenciez la série pour\( \dfrac{1}{\sqrt{1+x}}\)
- Réponse
-
\(\displaystyle \sum_{n=1}^∞\dfrac{(−1)^n}{n!}\dfrac{1⋅3⋅5⋯(2n−1)}{2^n}x^n\)
Dans cet exemple, nous avons différencié une série de Taylor connue pour construire une série de Taylor pour une autre fonction. La capacité de différencier les séries de puissances terme par terme en fait un outil puissant pour résoudre des équations différentielles. Nous montrons maintenant comment cela se fait.
Résolution d'équations différentielles avec Power Series
Considérez l'équation différentielle
\[y′(x)=y.\nonumber \]
Rappelez-vous qu'il s'agit d'une équation séparable du premier ordre et que sa solution est\(y=Ce^x\). Cette équation est facilement résolue à l'aide des techniques décrites plus haut dans le texte. Pour la plupart des équations différentielles, nous ne disposons toutefois pas encore d'outils analytiques pour les résoudre. Les séries de puissances sont un outil extrêmement utile pour résoudre de nombreux types d'équations différentielles. Dans cette technique, nous cherchons une solution de la forme\(\displaystyle y=\sum_{n=0}^∞c_nx^n\) et déterminons quels devraient être les coefficients. Dans l'exemple suivant, nous considérons un problème de valeur initiale impliquant\(y′=y\) d'illustrer la technique.
Utilisez la série Power pour résoudre le problème de la valeur initiale\(y′=y,\quad y(0)=3.\)
Solution
Supposons qu'il existe une solution de série électrique
\(\displaystyle y(x)=\sum_{n=0}^∞c_nx^n=c_0+c_1x+c_2x^2+c_3x^3+c_4x^4+⋯.\)
En différenciant cette série terme par terme, nous obtenons
\( y′=c_1+2c_2x+3c_3x^2+4c_4x^3+⋯.\)
Si\(y\) satisfait à l'équation différentielle, alors
\( c_0+c_1x+c_2x^2+c_3x^3+⋯=c_1+2c_2x+3c_3x^2+4c_3x^3+⋯.\)
En utilisant le caractère unique des représentations des séries de puissance, nous savons que ces séries ne peuvent être égales que si leurs coefficients sont égaux. Par conséquent,
\( c_0=c_1,\)
\( c_1=2c_2,\)
\( c_2=3c_3,\)
\( c_3=4c_4,\)
+1
Utilisation de la condition initiale\( y(0)=3\) combinée à la représentation de la série de puissances
\( y(x)=c_0+c_1x+c_2x^2+c_3x^3+⋯\),
c'est ce que nous constatons\( c_0=3\). Nous sommes maintenant prêts à résoudre le reste des coefficients. En utilisant le fait que\( c_0=3\), nous avons
\ [\ begin {align*} c_1&=c_0=3= \ dfrac {3} {1 !} , \ \ [5 points]
c_2&= \ dfrac {c_1} {2} = \ dfrac {3} {2} = \ dfrac {3} {2 !} , \ \ [5 points]
c_3&= \ dfrac {c_2} {3} = \ dfrac {3} {3⋅2} = \ dfrac {3} {3} {3 !} , \ \ [5 points]
c_4&= \ dfrac {c_3} {4} = \ dfrac {3} {4⋅3⋅2} = \ dfrac {3} {4 !}. \ end {align*} \]
Par conséquent,
\[y=3\left[1+\dfrac{1}{1!}x+\dfrac{1}{2!}x^2+\dfrac{1}{3!}x^3\dfrac{1}{4!}x^4+⋯\right]=3\sum_{n=0}^∞\dfrac{x^n}{n!}.\nonumber \]
Vous pourriez reconnaître
\[\sum_{n=0}^∞\dfrac{x^n}{n!}\nonumber \]
comme la série Taylor pour\( e^x\). La solution est donc\( y=3e^x\).
Utilisez les séries Power pour résoudre\( y′=2y,\quad y(0)=5.\)
- Allusion
-
Les équations des premiers coefficients\( c_n\) satisferont\( c_0=2c_1,\,c_1=2⋅2c_2,\,c_2=2⋅3c_3,\,….\) en général, pour tous\( n≥0,\;c_n=2(n+1)C_{n+1}\).
- Réponse
-
\( y=5e^{2x}\)
Nous examinons maintenant un exemple impliquant une équation différentielle que nous ne pouvons pas résoudre à l'aide des méthodes décrites précédemment. Cette équation différentielle
\[y′−xy=0\nonumber \]
est connue sous le nom d'équation d'Airy. Il a de nombreuses applications en physique mathématique, telles que la modélisation de la diffraction de la lumière. Nous montrons ici comment le résoudre en utilisant Power Series.
Utilisez des séries de puissance pour résoudre les problèmes\(y''−xy=0\) avec les conditions initiales\( y(0)=a\) et\( y'(0)=b.\)
Solution
Nous cherchons une solution du formulaire
\[y=\sum_{n=0}^∞c_nx^n=c_0+c_1x+c_2x^2+c_3x^3+c_4x^4+⋯\nonumber \]
En différenciant cette fonction terme par terme, nous obtenons
\ [\ begin {align*} y′&=c_1+2c_2x+3c_3x^2+4c_4x^3+, \ \ [4pt]
y"&=2⋅1c_2+3⋅2c_3x+4⋅3c_4x^2+. \ end {align*} \]
Si\(y\) répond à l'équation\( y''=xy\), alors
\( 2⋅1c_2+3⋅2c_3x+4⋅3c_4x^2+⋯=x(c_0+c_1x+c_2x^2+c_3x^3+⋯).\)
En utilisant [lien] sur le caractère unique des représentations des séries de puissances, nous savons que les coefficients du même degré doivent être égaux. Par conséquent,
\( 2⋅1c_2=0,\)
\( 3⋅2c_3=c_0,\)
\( 4⋅3c_4=c_1,\)
\( 5⋅4c_5=c_2,\)
+1
Plus généralement, pour\( n≥3\), nous avons\( n⋅(n−1)c_n=c_{n−3}\). En fait, tous les coefficients peuvent être écrits en termes de\( c_0\) et\( c_1\). Pour voir cela, notez d'abord que\( c_2=0\). Alors
\( c_3=\dfrac{c_0}{3⋅2}\),
\( c_4=\dfrac{c_1}{4⋅3}\).
Car\( c_5,\,c_6,\,c_7\), nous voyons que
\ [\ begin {align*} c_5&= \ dfrac {c_2} {5⋅4} =0, \ \ [5 points]
c_6&= \ dfrac {c_3} {6⋅5} = \ dfrac {c_0} {6⋅5⋅3⋅2}, \ \ [5 points]
c_7&= \ dfrac {c_4} 7⋅6} = \ dfrac {c_1} {7⋅6⋅4⋅3}. \ end {align*} \]
Par conséquent, la solution en série de l'équation différentielle est donnée par
\( y=c_0+c_1x+0⋅x^2+\dfrac{c_0}{3⋅2}x^3+\dfrac{c_1}{4⋅3}x^4+0⋅x^5+\dfrac{c_0}{6⋅5⋅3⋅2}x^6+\dfrac{c_1}{7⋅6⋅4⋅3}x^7+⋯.\)
La condition initiale\( y(0)=a\) implique\( c_0=a\). En différenciant cette série terme par terme et en utilisant le fait que\( y′(0)=b\), nous concluons que\( c_1=b\).
Par conséquent, la solution à ce problème de valeur initiale est
\( y=a\left(1+\dfrac{x^3}{3⋅2}+\dfrac{x}{6⋅5⋅3⋅2}+⋯\right)+b\left(x+\dfrac{x^4}{4⋅3}+\dfrac{x^7}{7⋅6⋅4⋅3}+⋯\right).\)
Utilisez des séries de puissance pour résoudre\( y''+x^2y=0\) avec la condition initiale\( y(0)=a\) et\( y′(0)=b\).
- Allusion
-
Les coefficients satisfont\( c_0=a,\,c_1=b,\,c_2=0,\,c_3=0,\) et pour\( n≥4,\; n(n−1)c_n=−c_{n−4}\).
- Réponse
-
\(y=a\left(1−\dfrac{x^4}{3⋅4}+\dfrac{x^8}{3⋅4⋅7⋅8}−⋯\right)+b\left(x−\dfrac{x^5}{4⋅5}+\dfrac{x^9}{4⋅5⋅8⋅9}−⋯\right)\)
Évaluation des intégrales non élémentaires
La résolution d'équations différentielles est une application courante des séries de puissances. Nous passons maintenant à une deuxième application. Nous montrons comment les séries de puissance peuvent être utilisées pour évaluer des intégrales impliquant des fonctions dont les antidérivées ne peuvent pas être exprimées à l'aide de fonctions élémentaires.
Une intégrale qui apparaît souvent dans les applications de la théorie des probabilités est\(\displaystyle \int e^{−x^2}\,dx.\) malheureusement que l'antidérivée de l'integrand n'\( e^{−x^2}\)est pas une fonction élémentaire. Par fonction élémentaire, nous entendons une fonction qui peut être écrite à l'aide d'un nombre fini de combinaisons algébriques ou de compositions de fonctions exponentielles, logarithmiques, trigonométriques ou de puissance. Nous remarquons que le terme « fonction élémentaire » n'est pas synonyme de fonction simple. Par exemple, la fonction\( f(x)=\sqrt{x^2−3x}+e^{x^3}−\sin(5x+4)\) est une fonction élémentaire, mais pas une fonction d'apparence particulièrement simple. Toute intégrale de la forme\(\displaystyle \int f(x)\,dx\) dont l'antidérivée de\( f\) ne peut pas être écrite en tant que fonction élémentaire est considérée comme une intégrale non élémentaire.
les intégrales non élémentaires ne peuvent pas être évaluées à l'aide des techniques d'intégration de base décrites précédemment. Une façon d'évaluer ces intégrales consiste à exprimer l'integrand sous forme de série de puissances et à intégrer terme par terme. Nous démontrons cette technique en considérant\(\displaystyle \int e^{−x^2}\,dx.\)
- Exprimez-vous\(\displaystyle \int e^{−x^2}dx\) sous forme de série infinie.
- \(\displaystyle \int ^1_0e^{−x^2}dx\)Évaluez avec une marge d'erreur de\( 0.01\).
Solution
a. La série Maclaurin pour\( e^{−x^2}\) est donnée par
\ [\ begin {align*} e^ {−x^2} &= \ sum_ {n=0} ^∞ \ dfrac {(−x^2) ^n} {n !} \ \ [5 points]
&=1−x^2+ \ dfrac {x^4} {2 !} − \ frac {x^6} {3 !} + (−1) ^n \ dfrac {x^ {2 n}} {n !} + \ \ [5 points]
&= \ sum_ {n=0} ^∞ (−1) ^n \ dfrac {x^ {2n}} {n !}. \ end {align*} \]
Par conséquent,
\ [\ begin {align*} \ int e^ {−x^2} \, dx&= \ int \ left (1−x^2+) \ dfrac {x^4} {2 !} − \ frac {x^6} {3 !} + (−1) ^n \ dfrac {x^ {2 n}} {n !} + \ right) \, dx \ \ [5 points]
&=C+X− \ dfrac {x^3} {3} + \ dfrac {x^5} {5,2 !} − \ frac {x^7} {7.3 !} + (−1) ^n \ dfrac {x^ {2n+1}} {(2n+1) n !} +. \ end {align*} \]
b. En utilisant le résultat de la partie a., nous avons
\[ \int ^1_0e^{−x^2}\,dx=1−\dfrac{1}{3}+\dfrac{1}{10}−\dfrac{1}{42}+\dfrac{1}{216}−⋯.\nonumber \]
La somme des quatre premiers termes est d'environ\( 0.74\). Par le test des séries alternées, cette estimation est précise avec une erreur inférieure à\( \dfrac{1}{216}≈0.0046296<0.01.\)
Exprimez-vous\(\displaystyle \int \cos\sqrt{x}\,dx\) sous forme de série infinie. \(\displaystyle \int ^1_0\cos\sqrt{x}\,dx\)Évaluez avec une marge d'erreur de\( 0.01\).
- Allusion
-
Utilisez la série trouvée dans Example\(\PageIndex{6}\).
- Réponse
-
\(\displaystyle C+\sum_{n=1}^∞(−1)^{n+1}\dfrac{x^n}{n(2n−2)!}\)L'intégrale définie est approximativement\( 0.514\) à une erreur de\( 0.01\).
Comme mentionné ci-dessus, l'intégrale\(\displaystyle \int e^{−x^2}\,dx\) apparaît souvent dans la théorie des probabilités. Plus précisément, il est utilisé pour étudier des ensembles de données qui sont normalement distribués, c'est-à-dire que les valeurs des données se situent sous une courbe en forme de cloche. Par exemple, si un ensemble de valeurs de données est normalement distribué avec une moyenne\( μ\) et un écart type\( σ\), la probabilité qu'une valeur choisie au hasard se situe entre\( x=a\) et\( x=b\) est donnée par
\[\dfrac{1}{σ\sqrt{2π}}\int ^b_ae^{−(x−μ)^2/(2σ^2)}\,dx.\label{probeq} \]
(Voir la figure\(\PageIndex{2}\).)
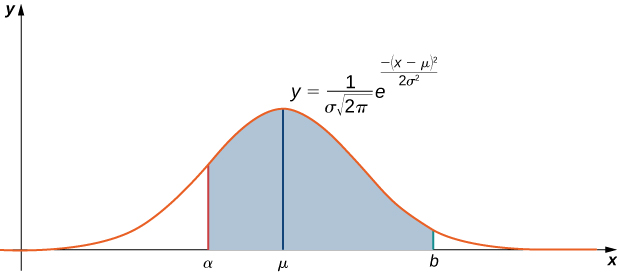
Pour simplifier cette intégrale, nous laissons généralement\( z=\dfrac{x−μ}{σ}\). Cette quantité\(z\) est connue sous le nom de\(z\) score d'une valeur de données. Avec cette simplification, l'équation intégrale \ ref {probeq} devient
\[\dfrac{1}{\sqrt{2π}}\int ^{(b−μ)/σ}_{(a−μ)/σ}e^{−z^2/2}\,dz. \nonumber \]
Dans Exemple\(\PageIndex{7}\), nous montrons comment utiliser cette intégrale pour calculer les probabilités.
Supposons qu'un ensemble de résultats de test standardisés soit normalement distribué avec une moyenne\( μ=100\) et un écart type\( σ=50\). Utilisez l'équation \ ref {probeq} et les six premiers termes de la série de Maclaurin pour\( e^{−x^2/2}\) approximer la probabilité qu'un score de test sélectionné au hasard se situe entre\( x=100\) et\( x=200\). Utilisez le test des séries alternées pour déterminer la précision de votre approximation.
Solution
Puisque\( μ=100,σ=50,\) et nous essayons de déterminer l'aire sous la courbe de\( a=100\) à\( b=200\), l'équation intégrale \ ref {probeq} devient
\[ \dfrac{1}{\sqrt{2π}}\int ^2_0e^{−z^2/2}\,dz.\nonumber \]
La série Maclaurin pour\( e^{−x^2/2}\) est donnée par
\ [\ begin {align*} e^ {−x^2/2} &= \ sum_ {n=0} ^∞ \ dfrac {\ left (− \ dfrac {x^2} {2} \ right) ^n} {n !} \ \ [5 points]
&=1− \ dfrac {x^2} {2^1⋅1 !} + \ dfrac {x^4} {2^2⋅2 !} − \ dfrac {x^6} {2^3⋅3 !} + (−1) ^n \ dfrac {x^ {2n}} {2^n⋅n} ! + \ \ [5 points]
&= \ sum_ {n=0} ^∞ (−1) ^n \ dfrac {x^ {2n}} {2^n⋅n !}. \ end {align*} \]
Par conséquent,
\ [\ begin {align*} \ dfrac {1} {\ sqrt {2π}} \ int e^ {−z^2/2} \, dz&= \ dfrac {1} {\ sqrt {2π}} \ int \ left (1− \ dfrac {z^2} {2^1⋅1 !} + \ dfrac {z^4} {2^2⋅2 !} − \ dfrac {z^6} {2^3⋅3 !} + (−1) ^n \ dfrac {z^ {2n}} {2^n⋅n !} + \ right) dz \ \ [5 points]
&= \ dfrac {1} {\ sqrt {2π}} \ left (C+z− \ dfrac {z^3} {3⋅2^1⋅1 !} + \ dfrac {z^5} {5⋅2^2⋅2 !} − \ dfrac {z^7} {7⋅2^3⋅3 !} + (−1) ^n \ dfrac {z^ {2n+1}} {(2n+1) 2^n⋅n !} +\ right) \ end {align*} \]
\[\dfrac{1}{\sqrt{2π}}\int ^2_0e^{−z^2/2}\,dz=\dfrac{1}{\sqrt{2π}}\left(2−\dfrac{8}{6}+\dfrac{32}{40}−\dfrac{128}{336}+\dfrac{512}{3456}−\dfrac{2^{11}}{11⋅2^5⋅5!}+⋯\right)\nonumber \]
À l'aide des cinq premiers termes, nous estimons que la probabilité est d'environ 0,4922. Par le test des séries alternées, nous constatons que cette estimation est précise à l'intérieur
\[ \dfrac{1}{\sqrt{2π}}\dfrac{2^{13}}{13⋅2^6⋅6!}≈0.00546.\nonumber \]
Analyse
Si vous connaissez la théorie des probabilités, vous savez peut-être que la probabilité qu'une valeur de données se situe à moins de deux écarts types de la moyenne est d'environ\( 95\%.\). Nous avons calculé la probabilité qu'une valeur de données se situe entre la moyenne et deux écarts types au-dessus de la moyenne, de sorte que l'estimation doit être autour de\( 47.5\%\). L'estimation, combinée à la limite de précision, se situe dans cette fourchette.
Utilisez les cinq premiers termes de la série de Maclaurin\( e^{−x^2/2}\) pour estimer la probabilité qu'un score de test sélectionné au hasard se situe entre\( 100\) et\( 150\). Utilisez le test des séries alternées pour déterminer la précision de cette estimation.
- Allusion
-
Évaluez\(\displaystyle \int ^1_0e^{−z^2/2}\,dz\) en utilisant les cinq premiers termes de la série Maclaurin pour\( e^{−z^2/2}\).
- Réponse
-
L'estimation est approximative.\( 0.3414.\) Cette estimation est précise à l'intérieur.\( 0.0000094.\)
Une autre application dans laquelle apparaît une intégrale non élémentaire concerne la période d'un pendule. L'intégrale est
\[\int ^{π/2}_0\dfrac{dθ}{\sqrt{1−k^2\sin^2θ}}\nonumber \].
Une intégrale de cette forme est connue sous le nom d'intégrale elliptique du premier type. Les intégrales elliptiques sont apparues à l'origine lors de la tentative de calcul de la longueur d'arc d'une ellipse. Nous montrons maintenant comment utiliser les séries de puissance pour approximer cette intégrale.
La période d'un pendule est le temps qu'il faut à un pendule pour effectuer un mouvement de va-et-vient complet. Pour un pendule dont la longueur\( L\) fait un angle maximal\( θ_{max}\) avec la verticale, sa période\( T\) est donnée par
\[ T=4\sqrt{\dfrac{L}{g}}\int ^{π/2}_0\dfrac{dθ}{\sqrt{1−k^2\sin^2θ}}\nonumber \]
où\( g\) est l'accélération due à la gravité et\( k=\sin\left(\dfrac{θ_{max}}{2}\right)\) (voir Figure\(\PageIndex{3}\)). (Nous remarquons que cette formule pour la période provient d'un modèle non linéarisé d'un pendule. Dans certains cas, à des fins de simplification, un modèle linéarisé est utilisé et\(\sin θ\) est approximé par\( θ\).)
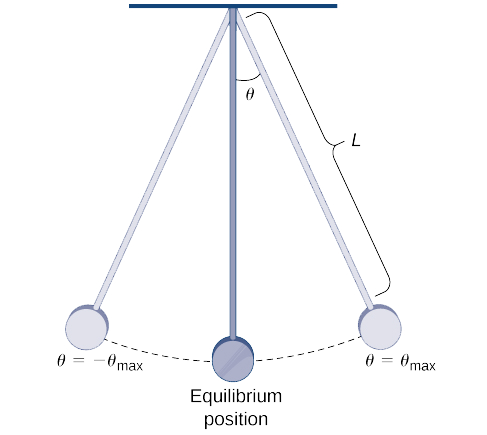
Utiliser la série binomiale
\[ \dfrac{1}{\sqrt{1+x}}=1+\sum_{n=1}^∞\dfrac{(−1)^n}{n!}\dfrac{1⋅3⋅5⋯(2n−1)}{2^n}x^n\nonumber \]
pour estimer la période de ce pendule. Plus précisément, approximez la période du pendule si
- vous utilisez uniquement le premier terme de la série binomiale, et
- vous utilisez les deux premiers termes de la série binomiale.
Solution
Nous utilisons la série binomiale, en remplaçant x par\( −k^2\sin^2θ.\) Ensuite, nous pouvons écrire le point comme
\[ T=4\sqrt{\dfrac{L}{g}}\int ^{π/2}_0\left(1+\dfrac{1}{2}k^2\sin^2θ+\dfrac{1⋅3}{2!2^2}k^4\sin^4θ+⋯\right)\,dθ.\nonumber \]
a. En utilisant uniquement le premier terme de l'integrand, l'estimation de premier ordre est
\[ T≈4\sqrt{\dfrac{L}{g}}\int ^{π/2}_0\,dθ=2π\sqrt{\dfrac{L}{g}}.\nonumber \]
Si\( θ_{max}\) c'est petit, alors\( k=\sin\left(\dfrac{θ_{max}}{2}\right)\) c'est petit. Nous prétendons que lorsqu'elle\( k\) est faible, c'est une bonne estimation. Pour justifier cette affirmation, considérez
\[ \int ^{π/2}_0\left(1+\frac{1}{2}k^2\sin^2θ+\dfrac{1⋅3}{2!2^2}k^4\sin^4θ+⋯\right)\,dθ.\nonumber \]
Puisque\( |\sin x|≤1\), cette intégrale est délimitée par
\[ \int ^{π/2}_0\left(\dfrac{1}{2}k^2+\dfrac{1.3}{2!2^2}k^4+⋯\right)\,dθ\;<\;\dfrac{π}{2}\left(\dfrac{1}{2}k^2+\dfrac{1⋅3}{2!2^2}k^4+⋯\right).\nonumber \]
En outre, on peut montrer que chaque coefficient sur le côté droit est inférieur à\( 1\) et, par conséquent, que cette expression est limitée par
\( \dfrac{πk^2}{2}(1+k^2+k^4+⋯)=\dfrac{πk^2}{2}⋅\dfrac{1}{1−k^2}\),
qui est petit pour\( k\) petit.
b. Pour des valeurs plus élevées de\( θ_{max}\), nous pouvons effectuer une approximation en\( T\) utilisant plus de termes dans l'integrand. En utilisant les deux premiers termes de l'intégrale, nous arrivons à l'estimation
\[ T≈4\sqrt{\frac{L}{g}}\int ^{π/2}_0\left(1+\dfrac{1}{2}k^2\sin^2θ\right)\,dθ=2π\sqrt{\dfrac{L}{g}}\left(1+\dfrac{k^2}{4}\right).\nonumber \]
Les applications de la série Taylor présentées dans cette section visent à souligner leur importance. En général, les séries de Taylor sont utiles car elles nous permettent de représenter des fonctions connues à l'aide de polynômes, nous fournissant ainsi un outil pour approximer les valeurs des fonctions et estimer des intégrales complexes. De plus, ils nous permettent de définir de nouvelles fonctions sous forme de séries de puissances, nous fournissant ainsi un outil puissant pour résoudre des équations différentielles.
Concepts clés
- La série binomiale est la série Maclaurin pour\( f(x)=(1+x)^r\). Il converge pour\( |x|<1\).
- Les séries de Taylor pour les fonctions peuvent souvent être dérivées par des opérations algébriques avec une série de Taylor connue ou en différenciant ou en intégrant une série de Taylor connue.
- Les séries de puissance peuvent être utilisées pour résoudre des équations différentielles.
- Les séries Taylor peuvent être utilisées pour aider à approximer des intégrales qui ne peuvent pas être évaluées par d'autres moyens.
Lexique
- série binomiale
- la série Maclaurin pour\( f(x)=(1+x)^r\) ; elle est donnée par\(\displaystyle (1+x)^r=\sum_{n=0}^∞\binom{r}{n}x^n=1+rx+\dfrac{r(r−1)}{2!}x^2+⋯+\dfrac{r(r−1)⋯(r−n+1)}{n!}x^n+⋯\) pour\( |x|<1\)
- intégrale non élémentaire
- une intégrale pour laquelle l'antidérivée de l'integrand ne peut pas être exprimée en tant que fonction élémentaire


