10.4E : Exercices pour la section 10.4

Last updated
Save as PDF

Page ID: 197144

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Dans les exercices 1 à 4, utilisez les substitutions appropriées pour noter la série de Maclaurin pour le binôme donné.

1)$(1−x)^{1/3}$

2)$(1+x^2)^{−1/3}$

Réponse: $\displaystyle (1+x^2)^{−1/3}=\sum_{n=0}^∞\left(n^{−\frac{1}{3}}\right)x^{2n}$

3)$(1−x)^{1.01}$

4)$(1−2x)^{2/3}$

Réponse: $\displaystyle (1−2x)^{2/3}=\sum_{n=0}^∞(−1)^n2^n\left(n^{\frac{2}{3}}\right)x^n$

Dans les exercices 5 à 12, utilisez la substitution$(b+x)^r=(b+a)^r\left(1+\dfrac{x−a}{b+a}\right)^r$ dans l'expansion binomiale pour trouver la série de Taylor de chaque fonction ayant un centre donné.

5)$\sqrt{x+2}$ à$a=0$

6)$\sqrt{x^2+2}$ à$a=0$

Réponse: $\displaystyle \sqrt{2+x^2}=\sum_{n=0}^∞2^{(1/2)−n}\left(n^{\frac{1}{2}}\right)x^{2n};(|x^2|<2)$

7)$\sqrt{x+2}$ à$a=1$

8)$\sqrt{2x−x^2}$ à$a=1$ (Astuce :$2x−x^2=1−(x−1)^2$)

Réponse: $\sqrt{2x−x^2}=\sqrt{1−(x−1)^2}$donc$\displaystyle \sqrt{2x−x^2}=\sum_{n=0}^∞(−1)^n\left(n^{\frac{1}{2}}\right)(x−1)^{2n}$

9)$(x−8)^{1/3}$ à$a=9$

10)$\sqrt{x}$ à$a=4$

Réponse: $\sqrt{x}=2\sqrt{1+\frac{x−4}{4}}$donc$\displaystyle \sqrt{x}=\sum_{n=0}^∞2^{1−2n}\left(n^{\frac{1}{2}}\right)(x−4)^n$

11)$x^{1/3}$ à$a=27$

12)$\sqrt{x}$ à$x=9$

Réponse: $\displaystyle \sqrt{x}=\sum_{n=0}^∞3^{1−3n}\left(n^{\frac{1}{2}}\right)(x−9)^n$

Dans les exercices 13 à 14, utilisez le théorème binomial pour estimer chaque nombre, en calculant suffisamment de termes pour obtenir une estimation précise à une erreur d'au plus$1/1000.$

13) [T]$(15)^{1/4}$ en utilisant$(16−x)^{1/4}$

14) [T]$(1001)^{1/3}$ en utilisant$(1000+x)^{1/3}$

Réponse: $\displaystyle 10(1+\frac{x}{1000})^{1/3}=\sum_{n=0}^∞10^{1−3n}(^{\frac{1}{3}}_n)x^n$. En utilisant, par exemple, une estimation au quatrième degré à$x=1$ donne$(1001)^{1/3}≈10\left(1+\left(1^{\frac{1}{3}}\right)10^{−3}+\left(2^{\frac{1}{3}}\right)10^{−6}+\left(3^{\frac{1}{3}}\right)10^{−9}+\left(3^{\frac{1}{3}}\right)10^{−12}\right)=10\left(1+\frac{1}{3.10^3}−\frac{1}{9.10^6}+\frac{5}{81.10^9}−\frac{10}{243.10^{12}}\right)=10.00333222...$ alors que$(1001)^{1/3}=10.00332222839093....$ deux termes suffiraient pour une précision à trois chiffres.

Dans les exercices 15 à 18, utilisez l'approximation binomiale$\sqrt{1−x}≈1−\frac{x}{2}−\frac{x^2}{8}−\frac{x^3}{16}−\frac{5x^4}{128}−\frac{7x^5}{256}$ pour$|x|<1$ obtenir une approximation de chaque nombre. Comparez cette valeur à la valeur donnée par une calculatrice scientifique.

15) [T]$\frac{1}{\sqrt{2}}$ utilisation$x=\frac{1}{2}$ dans$(1−x)^{1/2}$

16) [T]$\sqrt{5}=5×\frac{1}{\sqrt{5}}$ utilisation$x=\frac{4}{5}$ dans$(1−x)^{1/2}$

Réponse: L'approximation est$2.3152$ ; la valeur CAS est$2.23….$

17) [T]$\sqrt{3}=\frac{3}{\sqrt{3}}$ utilisation$x=\frac{2}{3}$ dans$(1−x)^{1/2}$

18) [T]$\sqrt{6}$ utilisation$x=\frac{5}{6}$ dans$(1−x)^{1/2}$

Réponse: L'approximation est$2.583…$ ; la valeur CAS est$2.449….$

19) Intégrez l'approximation binomiale de$\sqrt{1−x}$ pour trouver une approximation de$\displaystyle ∫^x_0\sqrt{1−t}\,dt$.

20) [T] Rappelez-vous que le graphe de$\sqrt{1−x^2}$ est un demi-cercle supérieur de rayon$1$. Intégrez l'approximation binomiale$\sqrt{1−x^2}$ allant$8$ de l'ordre$x=−1$$x=1$ à l'estimation$\frac{π}{2}$.

Réponse: $\sqrt{1−x^2}=1−\frac{x^2}{2}−\frac{x^4}{8}−\frac{x^6}{16}−\frac{5x^8}{128}+⋯.$Ainsi,$\displaystyle ∫^1_{−1}\sqrt{1−x^2}\,dx=\left[x−\frac{x^3}{6}−\frac{x^5}{40}−\frac{x^7}{7⋅16}−\frac{5x^9}{9⋅128}+⋯\right]\Big|^1_{−1}≈2−\frac{1}{3}−\frac{1}{20}−\frac{1}{56}−\frac{10}{9⋅128}+error=1.590...$ alors que$\frac{π}{2}=1.570...$

Dans les exercices 21 à 24, utilisez l'extension$(1+x)^{1/3}=1+\frac{1}{3}x−\frac{1}{9}x^2+\frac{5}{81}x^3−\frac{10}{243}x^4+⋯$ pour écrire les cinq premiers termes (pas nécessairement un polynôme quartique) de chaque expression.

(21)$(1+4x)^{1/3};\;a=0$

22)$(1+4x)^{4/3};\;a=0$

Réponse: $(1+x)^{4/3}=(1+x)(1+\frac{1}{3}x−\frac{1}{9}x^2+\frac{5}{81}x^3−\frac{10}{243}x^4+⋯)=1+\frac{4x}{3}+\frac{2x^2}{9}−\frac{4x^3}{81}+\frac{5x^4}{243}+⋯$

23)$(3+2x)^{1/3};\;a=−1$

(24)$(x^2+6x+10)^{1/3};\;a=−3$

Réponse: $(1+(x+3)^2)^{1/3}=1+\frac{1}{3}(x+3)^2−\frac{1}{9}(x+3)^4+\frac{5}{81}(x+3)^6−\frac{10}{243}(x+3)^8+⋯$

25) À utiliser$(1+x)^{1/3}=1+\frac{1}{3}x−\frac{1}{9}x^2+\frac{5}{81}x^3−\frac{10}{243}x^4+⋯$ avec$x=1$ à des fins approximatives$2^{1/3}$.

26) Utilisez l'approximation$(1−x)^{2/3}=1−\frac{2x}{3}−\frac{x^2}{9}−\frac{4x^3}{81}−\frac{7x^4}{243}−\frac{14x^5}{729}+⋯$$|x|<1$ pour approximer$2^{1/3}=2.2^{−2/3}$.

Réponse: Le double de l'approximation correspond$1.260…$ à$2^{1/3}=1.2599....$

27) Trouvez la$25^{\text{th}}$ dérivée de$f(x)=(1+x^2)^{13}$ at$x=0$.

28) Trouvez la$99^{\text{th}}$ dérivée de$f(x)=(1+x^4)^{25}$.

Réponse: $f^{(99)}(0)=0$

Dans les exercices 29 à 36, trouvez la série de Maclaurin de chaque fonction.

(29)$f(x)=xe^{2x}$

30)$f(x)=2^x$

Réponse: $\displaystyle \sum_{n=0}^∞\frac{(\ln(2)x)^n}{n!}$

31)$f(x)=\dfrac{\sin x}{x}$

32)$f(x)=\dfrac{\sin(\sqrt{x})}{\sqrt{x}},(x>0),$

Réponse: Pour$\displaystyle x>0,\, \sin(\sqrt{x})=\sum_{n=0}^∞(−1)^n\frac{x^{(2n+1)/2}}{\sqrt{x}(2n+1)!}=\sum_{n=0}^∞(−1)^n\frac{x^n}{(2n+1)!}$.

33)$f(x)=\sin(x^2)$

34)$f(x)=e^{x^3}$

Réponse: $\displaystyle e^{x^3}=\sum_{n=0}^∞\frac{x^{3n}}{n!}$

35)$f(x)=\cos^2x$ utilisation de l'identité$\cos^2x=\frac{1}{2}+\frac{1}{2}\cos(2x)$

36)$f(x)=\sin^2x$ utilisation de l'identité$\sin^2x=\frac{1}{2}−\frac{1}{2}\cos(2x)$

Réponse: $\displaystyle \sin^2x=−\sum_{k=1}^∞\frac{(−1)^k2^{2k−1}x^{2k}}{(2k)!}$

Dans les exercices 37 à 44, trouvez la série de Maclaurin en$\displaystyle F(x)=∫^x_0f(t)\,dt$ intégrant la série de Maclaurin$f$ terme par terme. Si$f$ ce n'est pas strictement défini à zéro, vous pouvez remplacer la valeur de la série de Maclaurin par zéro.

37)$\displaystyle F(x)=∫^x_0e^{−t^2}\,dt;\; f(t)=e^{−t^2}=\sum_{n=0}^∞(−1)^n\frac{t^{2n}}{n!}$

38)$\displaystyle F(x)=\tan^{−1}x;\; f(t)=\frac{1}{1+t^2}=\sum_{n=0}^∞(−1)^nt^{2n}$

Réponse: $\displaystyle \tan^{−1}x=\sum_{k=0}^∞\frac{(−1)^kx^{2k+1}}{2k+1}$

39)$\displaystyle F(x)=\tanh^{−1}x; \; f(t)=\frac{1}{1−t^2}=\sum_{n=0}^∞t^{2n}$

40)$\displaystyle F(x)=\sin^{−1}x; \; f(t)=\frac{1}{\sqrt{1−t^2}}=\sum_{k=0}^∞\left(k^{\frac{1}{2}}\right)\frac{t^{2k}}{k!}$

Réponse: $\displaystyle \sin^{−1}x=\sum_{n=0}^∞\left(n^{\frac{1}{2}}\right)\frac{x^{2n+1}}{(2n+1)n!}$

41)$\displaystyle F(x)=∫^x_0\frac{\sin t}{t}\,dt; \; f(t)=\frac{\sin t}{t}=\sum_{n=0}^∞(−1)^n\frac{t^{2n}}{(2n+1)!}$

42)$\displaystyle F(x)=∫^x_0\cos\left(\sqrt{t}\right)\,dt; \; f(t)=\sum_{n=0}^∞(−1)^n\frac{x^n}{(2n)!}$

Réponse: $\displaystyle F(x)=\sum_{n=0}^∞(−1)^n\frac{x^{n+1}}{(n+1)(2n)!}$

43)$\displaystyle F(x)=∫^x_0\frac{1−\cos t}{t^2}\,dt; \; f(t)=\frac{1−\cos t}{t^2}=\sum_{n=0}^∞(−1)^n\frac{t^{2n}}{(2n+2)!}$

44)$\displaystyle F(x)=∫^x_0\frac{\ln(1+t)}{t}\,dt; \; f(t)=\sum_{n=0}^∞(−1)^n\frac{t^n}{n+1}$

Réponse: $\displaystyle F(x)=\sum_{n=1}^∞(−1)^{n+1}\frac{x^n}{n^2}$

Dans les exercices 45 à 52, calculez au moins les trois premiers termes non nuls (pas nécessairement un polynôme quadratique) de la série de Maclaurin de$f$.

45)$f(x)=\sin\left(x+\frac{π}{4}\right)=\sin x\cos\left(\frac{π}{4}\right)+\cos x\sin\left(\frac{π}{4}\right)$

46)$f(x)=\tan x$

Réponse: $x+\dfrac{x^3}{3}+\dfrac{2x^5}{15}+⋯$

47)$f(x)=\ln(\cos x)$

48)$f(x)=e^x\cos x$

Réponse: $1+x−\dfrac{x^3}{3}−\dfrac{x^4}{6}+⋯$

49)$f(x)=e^{\sin x}$

50)$f(x)=\sec^2x$

Réponse: $1+x^2+\dfrac{2x^4}{3}+\dfrac{17x^6}{45}+⋯$

51)$f(x)=\tanh x$

52)$f(x)=\dfrac{\tan\sqrt{x}}{\sqrt{x}}$ (voir extension pour$\tan x$)

Réponse: Utiliser l'extension pour$\tan x$ donner$1+\dfrac{x}{3}+\dfrac{2x^2}{15}$.

Dans les exercices 53 à 56, déterminez le rayon de convergence de la série de Maclaurin de chaque fonction.

53)$\ln(1+x)$

(54)$\dfrac{1}{1+x^2}$

Réponse: $\displaystyle \frac{1}{1+x^2}=\sum_{n=0}^∞(−1)^nx^{2n}$donc$R=1$ par le test du ratio.

55)$\tan^{−1}x$

(56)$\ln(1+x^2)$

Réponse: $\displaystyle \ln(1+x^2)=\sum_{n=1}^∞\frac{(−1)^{n−1}}{n}x^{2n}$donc$R=1$ par le test du ratio.

57) Retrouvez la série Maclaurin de$\sinh x=\dfrac{e^x−e^{−x}}{2}$.

58) Retrouvez la série Maclaurin de$\cosh x=\dfrac{e^x+e^{−x}}{2}$.

Réponse: Ajoutez une série de$e^x$ et$e^{−x}$ terme par terme. Des termes étranges annulent et$\displaystyle \cosh x=\sum_{n=0}^∞\frac{x^{2n}}{(2n)!}$.

59) Différenciez terme par terme la série de Maclaurin de$\sinh x$ et comparez le résultat avec la série de Maclaurin de$\cosh x$.

60) [T] Soit$\displaystyle S_n(x)=\sum_{k=0}^n(−1)^k\frac{x^{2k+1}}{(2k+1)!}$ et$\displaystyle C_n(x)=\sum_{n=0}^n(−1)^k\frac{x^{2k}}{(2k)!}$ dénotent les polynômes de Maclaurin respectifs de degré$\sin x$ et$2n+1$ de degré$2n$ de$\cos x$. Tracez les erreurs$\dfrac{S_n(x)}{C_n(x)}−\tan x$ pour$n=1,..,5$ et comparez-les à$x+\dfrac{x^3}{3}+\dfrac{2x^5}{15}+\dfrac{17x^7}{315}−\tan x$ on$\left(−\frac{π}{4},\frac{π}{4}\right)$.

Réponse

Le ratio$\dfrac{S_n(x)}{C_n(x)}$ se rapproche$\tan x$ mieux que$p_7(x)=x+\dfrac{x^3}{3}+\dfrac{2x^5}{15}+\dfrac{17x^7}{315}$ pour$N≥3$. Les courbes en pointillés sont$\dfrac{S_n}{C_n}−\tan x$ pour$n=1,\, 2$. La courbe en pointillés correspond à$n=3$, et la courbe en pointillés correspond à$n=4$. La courbe continue est$p_7−\tan x$.

$Ce graphique comporte deux courbes. La première est une fonction décroissante passant par l'origine. La seconde est une ligne brisée qui est une fonction croissante passant par l'origine. Les deux courbes sont très proches de l'origine.$

61) Utilisez l'identité$2\sin x\cos x=\sin(2x)$ pour trouver l'extension de la série Power de$\sin^2x$ at$x=0$. (Conseil : intégrez la série Maclaurin$\sin(2x)$ terme par terme.)

62) Si$\displaystyle y=\sum_{n=0}^∞a_nx^n$, trouvez les extensions de la série Power de$xy′$ et$x^2y''$.

Réponse: Par le théorème de différenciation terme par terme$\displaystyle y′=\sum_{n=1}^∞na_nx^{n−1}xy′=\sum_{n=1}^∞na_nx^n$,$\displaystyle y′=\sum_{n=1}^∞na_nx^{n−1}$ alors que$\displaystyle y′=\sum_{n=2}^∞n(n−1)a_nx^{n−2}$ oui$\displaystyle xy''=\sum_{n=2}^∞n(n−1)a_nx^n$.

63) [T] Supposons que cela$\displaystyle y=\sum_{k=0}^∞a^kx^k$ satisfait$y′=−2xy$ et$y(0)=0$. Montrez cela$a_{2k+1}=0$ à tous$k$ et à cela$a_{2k+2}=\dfrac{−a_{2k}}{k+1}$. Tracez la somme partielle$S_{20}$ de$y$ sur l'intervalle$[−4,4]$.

64) [T] Supposons qu'un ensemble de résultats de test standardisés soit normalement distribué avec une moyenne$μ=100$ et un écart type$σ=10$. Définissez une intégrale qui représente la probabilité qu'un résultat de test se situe entre$90$ et$110$ et utilisez l'intégrale du degré polynôme de$10$ Maclaurin$\frac{1}{\sqrt{2π}}e^{−x^2/2}$ pour estimer cette probabilité.

Réponse: La probabilité est de$\displaystyle p=\frac{1}{\sqrt{2π}}∫^{(b−μ)/σ}_{(a−μ)/σ}e^{−x^2/2}\,dx$ savoir où$a=90$ et$b=100$, c'est-à-dire,$\displaystyle p=\frac{1}{\sqrt{2π}}∫^1_{−1}e^{−x^2/2}\,dx=\frac{1}{\sqrt{2π}}∫^1_{−1}\sum_{n=0}^5(−1)^n\frac{x^{2n}}{2^nn!}\,dx=\frac{2}{\sqrt{2π}}\sum_{n=0}^5(−1)^n\frac{1}{(2n+1)2^nn!}≈0.6827.$

65) [T] Supposons qu'un ensemble de résultats de test standardisés soit normalement distribué avec une moyenne$μ=100$ et un écart type$σ=10$. Définissez une intégrale qui représente la probabilité qu'un résultat de test se situe entre$70$ et$130$ et utilisez l'intégrale du degré polynôme de$50$ Maclaurin$\frac{1}{\sqrt{2π}}e^{−x^2/2}$ pour estimer cette probabilité.

66) [T] Supposons que cela$\displaystyle \sum_{n=0}^∞a_nx^n$ converge vers une fonction$f(x)$ telle que$f(0)=1,\, f′(0)=0$, et$f''(x)=−f(x)$. Trouvez une formule pour$a_n$ et tracez la somme partielle$S_N$ pour$N=20$$[−5,5].$

Réponse

Comme dans le problème précédent, on obtient$a_n=0$ si$n$ est impair et$a_n=−(n+2)(n+1)a_{n+2}$ si$n$ est pair,$a_0=1$ ce qui conduit à$a_{2n}=\dfrac{(−1)^n}{(2n)!}$.

$Ce graphique est une courbe d'onde symétrique par rapport à l'origine. Elle a un pic à y = 1 au-dessus de l'origine. Il a les points les plus bas à -3 et 3.$

67) [T] Supposons que cela$\displaystyle \sum_{n=0}^∞a_nx^n$ converge vers une fonction$f(x)$ telle que$f(0)=0,\; f′(0)=1$, et$f''(x)=−f(x)$. Trouvez une formule pour un et tracez la somme partielle$S_N$ pour$N=10$ un$[−5,5]$.

68) Supposons que cela$\displaystyle \sum_{n=0}^∞a_nx^n$ converge vers une fonction$y$ telle que$y''−y′+y=0$ Where$y(0)=1$ et$y'(0)=0.$ Find une formule qui relie$a_{n+2},\;a_{n+1},$ et un et calcule$a_0,...,a_5$.

Réponse: $\displaystyle y''=\sum_{n=0}^∞(n+2)(n+1)a_{n+2}x^n$et$\displaystyle y′=\sum_{n=0}^∞(n+1)a_{n+1}x^n$ donc$y''−y′+y=0$ implique cela$(n+2)(n+1)a_{n+2}−(n+1)a_{n+1}+a_n=0$ ou$a_n=\dfrac{a_{n−1}}{n}−\dfrac{a_{n−2}}{n(n−1)}$ pour tous$n⋅y(0)=a_0=1$ et$y′(0)=a_1=0,$ ainsi de suite$a_2=\frac{1}{2},\;a_3=\frac{1}{6}\;,a_4=0$, et$a_5=−\frac{1}{120}$.

69) Supposons que cela$\displaystyle \sum_{n=0}^∞a_nx^n$ converge vers une fonction$y$ telle que$y''−y′+y=0$ où$y(0)=0$ et$y′(0)=1$. Trouvez une formule qui met en$a_{n+2},\;a_{n+1}$ relation, et un et calcule$a_1,...,a_5$.

L'erreur d'approximation de l'intégrale$\displaystyle ∫^b_af(t)\, dt$ par celle d'une approximation de Taylor$\displaystyle ∫^b_aPn(t) \,dt$ est maximale$\displaystyle ∫^b_aR_n(t) \,dt$. Dans les exercices 70 à 71, l'estimation du reste de Taylor$R_n≤\frac{M}{(n+1)!}|x−a|^{n+1}$ garantit que l'intégrale du polynôme de Taylor de l'ordre donné se rapproche de l'intégrale de$f$ avec une erreur inférieure à$\frac{1}{10}$.

a. Évaluez l'intégrale du polynôme de Taylor approprié et vérifiez qu'elle se rapproche de la valeur CAS avec une erreur inférieure à$\frac{1}{100}$.

b. Comparez la précision de l'estimation intégrale polynomiale avec l'estimation du reste.

70) [T]$\displaystyle ∫^π_0\frac{\sin t}{t}\, dt;\quad P_s=1−\frac{x^2}{3!}+\frac{x^4}{5!}−\frac{x^6}{7!}+\frac{x^8}{9!}$ (Vous pouvez supposer que la valeur absolue de la dérivée neuvième de$\frac{\sin t}{t}$ est limitée par$0.1$.)

Réponse: a. (Preuve)
b.$R_s≤\frac{0.1}{(9)!}π^9≈0.0082<0.01.$ Nous avons$\displaystyle ∫^π_0\left(1−\frac{x^2}{3!}+\frac{x^4}{5!}−\frac{x^6}{7!}+\frac{x^8}{9!}\right)\,dx=π−\frac{π^3}{3⋅3!}+\frac{π^5}{5⋅5!}−\frac{π^7}{7⋅7!}+\frac{π^9}{9⋅9!}=1.852...,$ alors que$\displaystyle ∫^π_0\frac{\sin t}{t}\,dt=1.85194...$, donc l'erreur réelle est d'environ$0.00006.$

71) [T]$\displaystyle ∫^2_0e^{−x^2}\,dx;\; p_{11}=1−x^2+\frac{x^4}{2}−\frac{x^6}{3!}+⋯−\frac{x^{22}}{11!}$ (Vous pouvez supposer que la valeur absolue de la$23^{\text{rd}}$ dérivée de$e^{−x^2}$ est inférieure à$2×10^{14}$.)

Les exercices suivants (72-73) traitent des intégrales de Fresnel.

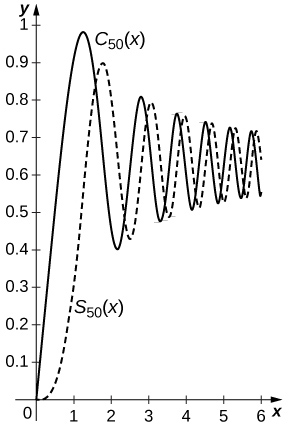
72) Les intégrales de Fresnel sont définies par$\displaystyle C(x)=∫^x_0\cos(t^2)\,dt$ et$\displaystyle S(x)=∫^x_0\sin(t^2)\,dt$. Calculez la série de puissance de$C(x)$$S(x)$ et et tracez les sommes$C_N(x)$ et$S_N(x)$ les premiers termes$N=50$ non nuls sur$[0,2π]$.

Réponse

Depuis$\displaystyle \cos(t^2)=\sum_{n=0}^∞(−1)^n\frac{t^{4n}}{(2n)!}$ et$\displaystyle \sin(t^2)=\sum_{n=0}^∞(−1)^n\frac{t^{4n+2}}{(2n+1)!}$, on a$\displaystyle S(x)=\sum_{n=0}^∞(−1)^n\frac{x^{4n+3}}{(4n+3)(2n+1)!}$ et$\displaystyle C(x)=\sum_{n=0}^∞(−1)^n\frac{x^{4n+1}}{(4n+1)(2n)!}$. Les sommes des premiers termes$50$ non nuls sont tracées ci-dessous avec$C_{50}(x)$ la courbe continue et$S_{50}(x)$ la courbe en pointillés.

$Ce graphique comporte deux courbes. La première est une courbe pleine étiquetée Csub50 (x). Elle commence à l'origine et est une onde dont l'amplitude diminue progressivement. Le plus haut qu'il atteint est y = 1. La deuxième courbe est étiquetée Ssub50 (x). C'est une onde dont l'amplitude diminue progressivement. Le plus haut qu'il atteint est de 0,9. Il est très proche du motif de la première courbe avec un léger décalage vers la droite.$

73) [T] Les intégrales de Fresnel sont utilisées dans les applications de conception pour les routes et les chemins de fer et dans d'autres applications en raison des propriétés de courbure de la courbe avec coordonnées$(C(t),S(t))$. Tracez la courbe$(C_{50},S_{50})$ pour$0≤t≤2π$, dont les coordonnées ont été calculées lors de l'exercice précédent.

74) Estimation$\displaystyle ∫^{1/4}_0\sqrt{x−x^2}\,dx$ par approximation à$\sqrt{1−x}$ l'aide de l'approximation binomiale$\displaystyle 1−\frac{x}{2}−\frac{x^2}{8}−\frac{x^3}{16}−\frac{5x^4}{2128}−\frac{7x^5}{256}$.

Réponse: $\displaystyle ∫^{1/4}_0\sqrt{x}\left(1−\frac{x}{2}−\frac{x^2}{8}−\frac{x^3}{16}−\frac{5x^4}{128}−\frac{7x^5}{256}\right)\,dx =\frac{2}{3}2^{−3}−\frac{1}{2}\frac{2}{5}2^{−5}−\frac{1}{8}\frac{2}{7}2^{−7}−\frac{1}{16}\frac{2}{9}2^{−9}−\frac{5}{128}\frac{2}{11}2^{−11}−\frac{7}{256}\frac{2}{13}2^{−13}=0.0767732...$tandis que$\displaystyle ∫^{1/4}_0\sqrt{x−x^2}\, dx=0.076773.$

75) [T] Utilisez l'approximation du binôme de Newton$\sqrt{1−x^2}$ pour obtenir une approximation$π$ comme suit. Le cercle centré$(\frac{1}{2},0)$ par un rayon$\frac{1}{2}$ possède un demi-cercle supérieur$y=\sqrt{x}\sqrt{1−x}$. Le secteur de ce cercle délimité par l'$x$axe -entre$x=0$ et$x=\frac{1}{2}$ et par la ligne joignant les lignes$(\frac{1}{4},\frac{\sqrt{3}}{4})$ correspond au$\frac{1}{6}$ cercle et possède une aire$\frac{π}{24}$. Ce secteur est l'union d'un triangle droit avec hauteur$\frac{\sqrt{3}}{4}$ et base$\frac{1}{4}$ et de la région située sous le graphique entre$x=0$ et$x=\frac{1}{4}$. Pour trouver la zone de cette région, vous pouvez écrire$y=\sqrt{x}\sqrt{1−x}=\sqrt{x}×(\text{binomial expansion of} \sqrt{1−x})$ et intégrer terme par terme. Utilisez cette approche avec l'approximation binomiale de l'exercice précédent pour effectuer une estimation$π$.

76) Utilisez l'approximation$T≈2π\sqrt{\frac{L}{g}}(1+\frac{k^2}{4})$ pour approximer la période d'un pendule ayant une longueur en$10$ mètres et un angle maximum$θ_{max}=\frac{π}{6}$ où$k=\sin\left(\frac{θ_{max}}{2}\right)$. Comparez cela avec l'estimation du petit angle$T≈2π\sqrt{\frac{L}{g}}$.

Réponse: $T≈2π\sqrt{\frac{10}{9.8}}\left(1+\frac{\sin^2(θ/12)}{4}\right)≈6.453$secondes. L'estimation du petit angle est de$T≈2π\sqrt{\frac{10}{9.8}≈6.347}$. L'erreur relative est d'environ un$2$ pour cent.

77) Supposons qu'un pendule ait une période de$2$ secondes et un angle maximum de$θ_{max}=\frac{π}{6}$. $T≈2π\sqrt{\dfrac{L}{g}}\left(1+\dfrac{k^2}{4}\right)$À utiliser pour obtenir une longueur approximative du pendule. Quelle longueur est prédite par l'estimation du petit angle$T≈2π\sqrt{\frac{L}{g}}$ ?

78) Évaluez$\displaystyle ∫^{π/2}_0\sin^4θ\,dθ$ par approximation$\displaystyle T=4\sqrt{\frac{L}{g}}∫^{π/2}_0\left(1+\frac{1}{2}k^2\sin^2θ+\frac{3}{8}k^4\sin^4θ+⋯\right)\,dθ$ pour obtenir une meilleure estimation pour$T$.

Réponse: $\displaystyle ∫^{π/2}_0\sin^4θ\, dθ=\frac{3π}{16}.$D'où$T≈2π\sqrt{\frac{L}{g}}\left(1+\frac{k^2}{4}+\frac{9}{256}k^4\right).$

79) [T] Une formule équivalente pour la période d'un pendule avec amplitude$\displaystyle θ_{max}$$L$ est$T(θ_{max})=2\sqrt{2}\sqrt{\frac{L}{g}}∫^{θ_{max}}_0\frac{dθ}{\sqrt{\cos θ}−\cos(θ_{max})}$ où sont la longueur du pendule et$g$ la constante d'accélération gravitationnelle. Quand$θ_{max}=\frac{π}{3}$ nous arriverons$\dfrac{1}{\sqrt{\cos t−1/2}}≈\sqrt{2}\left(1+\frac{t^2}{2}+\frac{t^4}{3}+\frac{181t^6}{720}\right)$. Intégrez cette approximation pour estimer$T(\frac{π}{3})$ en termes de$L$ et$g$. En supposant des$g=9.806$ mètres par seconde au carré, trouvez une longueur approximative$L$ telle que$T(\frac{π}{3})=2$ secondes.

Contributeurs

Template:ContribOpenStaxCalc