9.5 : Séries alternées
- Page ID
- 197697
- Utilisez le test des séries alternées pour tester la convergence d'une série alternative.
- Estimez la somme d'une série alternée.
- Expliquez la signification de la convergence absolue et de la convergence conditionnelle.
Jusqu'à présent, dans ce chapitre, nous avons principalement discuté de séries contenant des termes positifs. Dans cette section, nous présentons les séries alternées, c'est-à-dire les séries dont les termes alternent en signes. Nous montrerons dans un chapitre ultérieur que ces séries apparaissent souvent lors de l'étude des séries de puissance. Après avoir défini les séries alternées, nous introduisons le test des séries alternées pour déterminer si une telle série converge.
Le test des séries alternées
Une série dont les termes alternent entre des valeurs positives et négatives est une série alternative. Par exemple, la série
\[\sum_{n=1}^∞ \left(−\dfrac{1}{2} \right)^n=−\dfrac{1}{2}+\dfrac{1}{4}−\dfrac{1}{8}+\dfrac{1}{16}− \ldots \label{eq1} \]
et
\[\sum_{n=1}^∞\dfrac{(−1)^{n+1}}{n}=1−\dfrac{1}{2}+\dfrac{1}{3}−\dfrac{1}{4}+\ldots \label{eq2} \]
sont toutes deux des séries alternées.
Toute série dont les termes alternent entre des valeurs positives et négatives est appelée série alternative. Une série alternée peut être écrite sous la forme
\[\sum_{n=1}^∞(−1)^{n+1}b_n=b_1−b_2+b_3−b_4+ \ldots \label{eq3} \]
ou
\[\sum_{n−1}^∞(−1)^nb_n=−b_1+b_2−b_3+b_4−\ldots \label{eq4} \]
Où\( b_n≥0\) pour tous les entiers positifs\(n\).
La série (1), présentée dans l'équation \ ref {eq1}, est une série géométrique. Depuis que\( |r|=|−1/2|<1,\) la série converge. La série (2), présentée dans l'équation \ ref {eq2}, est appelée série harmonique alternée. Nous montrerons que tandis que la série harmonique diverge, la série harmonique alternative converge. Pour le prouver, nous examinons la séquence des sommes partielles\( \{S_k\}\) (Figure 1).
Considérez les termes étranges\( S_{2k+1}\) pour\( k≥0\). Depuis\( 1/(2k+1)<1/2k,\)
\[S_{2k+1}=S_{2k−1}−\dfrac{1}{2k}+\dfrac{1}{2k+1}<S_{2k−1}. \nonumber \]
Par conséquent,\( \{S_{2k+1}\}\) est une séquence décroissante. En outre,
\[S_{2k+1}=\left(1−\dfrac{1}{2}\right)+\left(\dfrac{1}{3}−\dfrac{1}{4}\right)+ \ldots + \left(\dfrac{1}{2k−1}−\dfrac{1}{2k}\right)+\dfrac{1}{2k+1}>0. \nonumber \]
Par conséquent,\( \{S_{2k+1}\}\) est limité ci-dessous. Puisque\( \{S_{2k+1}\}\) est une séquence décroissante qui est limitée ci-dessous, par le théorème de convergence monotone,\( \{S_{2k+1}\}\) converge. De même, les termes pairs\( \{S_{2k}\}\) forment une séquence croissante qui est bornée au-dessus parce que
\[S_{2k}=S_{2k−2}+\dfrac{1}{2k−1}−\dfrac{1}{2k}>S_{2k−2} \nonumber \]
et
\[S_{2k}=1+ \left(−\dfrac{1}{2}+\dfrac{1}{3}\right)+\ldots + \left(−\dfrac{1}{2k−2}+\dfrac{1}{2k−1}\right)−\dfrac{1}{2k}<1. \nonumber \]
Par conséquent, selon le théorème de convergence monotone, la séquence converge\( \{S_{2k}\}\) également. Depuis
\[S_{2k+1}=S_{2k}+\dfrac{1}{2k+1}, \nonumber \]
nous savons que
\[\lim_{k→∞}S_{2k+1}=\lim_{k→∞}S_{2k}+\lim_{k→∞}\dfrac{1}{2k+1}. \nonumber \]
Laissant\(\displaystyle S=\lim_{k→∞}S_{2k+1}\) et utilisant le fait que\( 1/(2k+1)→0,\) nous en concluons\(\displaystyle \lim_{k→∞}S_{2k}=S\). Puisque les termes impairs et les termes pairs de la séquence de sommes partielles convergent vers la même limite\( S\), il peut être démontré que la séquence de sommes partielles converge vers et\( S\), par conséquent, la série harmonique alternée converge vers\( S\).
On peut aussi le montrer\( S=\ln 2,\) et on peut écrire
\[\sum_{n=1}^∞\dfrac{(−1)^{n+1}}{n}=1−\dfrac{1}{2}+\dfrac{1}{3}−\dfrac{1}{4}+a\ldots=\ln (2). \nonumber \]
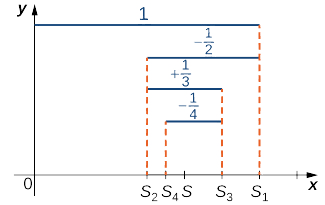
□
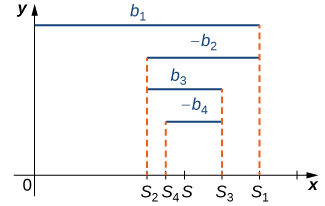
Plus généralement, toute série alternée de forme (3) (Équation \ ref {eq3}) ou (4) (Équation \ ref {eq4}) converge tant que\( b_1≥b_2≥b_3≥⋯\) et\( b_n→0\) (Figure 2). La preuve est similaire à celle de la série harmonique alternée.
Une série alternée du formulaire
\[\sum_{n=1}^∞(−1)^{n+1}b_n \nonumber \]ou\[\sum_{n=1}^∞(−1)^nb_n \nonumber \]
converge si
- \( 0≤b_{n+1}≤b_n\)pour tous\( n≥1\) et
- \(\displaystyle \lim_{n→∞}b_n=0.\)
C'est ce que l'on appelle le test en série alternée.
Nous remarquons que ce théorème est vrai plus généralement tant qu'il existe un entier\( N\) tel que\( 0≤b_{n+1}≤b_n\) pour tous\( n≥N.\)
Pour chacune des séries alternées suivantes, déterminez si la série converge ou diverge.
- \(\displaystyle \sum^∞_{n=1}\frac{(−1)^{n+1}}{n^2}\)
- \(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\frac{n}{n+1}\)
Solution
a. Depuis\( \dfrac{1}{(n+1)^2}<\dfrac{1}{n^2}\) et\( \dfrac{1}{n^2}→0,\) la série converge.
b. Dans la\( n/(n+1)↛0\) mesure où\( n→∞\), nous ne pouvons pas appliquer le test des séries alternées. Nous utilisons plutôt le nième terme test pour la divergence. Puisque\(\displaystyle \lim_{n→∞}\dfrac{n}{n+1}=1≠0,\) la série diverge.
Déterminez si la série\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\frac{n}{2^n}\) converge ou diverge.
- Allusion
-
Est\( \left\{\frac{n}{2^n}\right\}\) en baisse ? Qu'\(\displaystyle \lim_{n→∞}\frac{n}{2^n}\)est-ce que c'est
- Réponse
-
La série converge.
Reste d'une série alternée
Comme il est difficile de calculer explicitement la somme de la plupart des séries alternées, la somme est généralement approximée à l'aide d'une somme partielle. Ce faisant, nous nous intéressons à la quantité d'erreur dans notre approximation. Envisagez une série alternée
\[\sum_{n=1}^∞(−1)^{n+1}b_n \nonumber \]
satisfaisant aux hypothèses du test en série alternée. \( S\)Dénotons la somme de cette série et\( {S_k}\) sommes la séquence correspondante de sommes partielles. Sur la figure\( \PageIndex{2}\), nous voyons que pour tout entier\( N≥1\), le reste\( R_N\) satisfait
\[|R_N|=|S−S_N|≤|S_{N+1}−S_N|=b_{n+1}. \nonumber \]
Considérez une série alternée du formulaire
\[\sum_{n=1}^∞(−1)^{n+1}b_n \nonumber \]ou\[\sum_{n=1}^∞(−1)^nb_n \nonumber \]
qui satisfait aux hypothèses du test en série alternée. \( S\)Dénotons la somme des séries et\( S_N\) dénotons la somme\(N^{\text{th}}\) partielle. Pour tout entier\( N≥1\), le reste\( R_N=S−S_N\) satisfait
\[|R_N|≤b_{N+1}. \nonumber \]
En d'autres termes, si les conditions du test des séries alternées s'appliquent, alors l'erreur d'approximation de la série infinie par la somme\(N^{\text{th}}\) partielle\( S_N\) est d'une ampleur tout au plus égale à la taille du terme suivant\( b_{N+1}\).
Considérez les séries alternées
\[ \sum_{n=1}^∞\dfrac{(−1)^{n+1}}{n^2}. \nonumber \]
Utilisez l'estimation du reste pour déterminer une limite de l'erreur\( R_{10}\) si nous approximons la somme des séries par la somme partielle\( S_{10}\).
Solution
D'après le théorème exposé ci-dessus,\[ |R_{10}|≤b_{11}=\dfrac{1}{11^2}≈0.008265. \nonumber \]
Trouvez une limite\( R_{20}\) lorsque vous vous\(\displaystyle \sum^∞_{n=1}\frac{(−1)^{n+1}}{n}\) approchez\( S_{20}\).
- Allusion
-
\( |R_{20}|≤b_{21}\)
- Réponse
-
\( 0.04762\)
Convergence absolue et conditionnelle
Prenons l'exemple d'une série\(\displaystyle \sum_{n=1}^∞a_n\) et des séries connexes\(\displaystyle \sum_{n=1}^∞|a_n|\). Nous discutons ici des possibilités de relation entre la convergence de ces deux séries. Par exemple, considérez les séries harmoniques alternées\(\displaystyle \sum_{n=1}^∞\frac{(−1)^{n+1}}{n}\). La série dont les termes sont la valeur absolue de ces termes est la série harmonique, puisque\(\displaystyle \sum_{n=1}^∞\left|\frac{(−1)^{n+1}}{n}\right|=\sum_{n=1}^∞\frac{1}{n}.\) puisque la série harmonique alternée converge, mais que la série harmonique diverge, nous disons que la série harmonique alternative présente une convergence conditionnelle.
Par comparaison, considérez la série\(\displaystyle \sum_{n=1}^∞\frac{(−1)^{n+1}}{n^2}.\) La série dont les termes sont les valeurs absolues des termes de cette série est la série\(\displaystyle \sum_{n=1}^∞\frac{1}{n^2}.\) Puisque ces deux séries convergent, nous disons que la série\(\displaystyle \sum_{n=1}^∞\frac{(−1)^{n+1}}{n^2}\) présente une convergence absolue.
Une série\(\displaystyle \sum^∞_{n=1}a_n\) présente une convergence absolue si elle\(\displaystyle \sum^∞_{n=1}|a_n|\) converge. Une série\(\displaystyle \sum^∞_{n=1}a_n\) présente une convergence conditionnelle si elle\(\displaystyle \sum^∞_{n=1}a_n\) converge mais\(\displaystyle \sum^∞_{n=1}|a_n|\) diverge.
Comme le montre la série harmonique alternée, une série\(\displaystyle \sum^∞_{n=1}a_n\) peut converger, mais\(\displaystyle \sum^∞_{n=1}|a_n|\) peut diverger. Dans le théorème suivant, cependant, nous montrons que si elle\(\displaystyle \sum^∞_{n=1}|a_n|\) converge, elle\(\displaystyle \sum^∞_{n=1}a_n\) converge.
Si\(\displaystyle \sum^∞_{n=1}|a_n|\) converge, puis\(\displaystyle \sum^∞_{n=1}a_n\) converge.
Supposons que cela\(\displaystyle \sum_{n=1}^∞|a_n|\) converge. Nous le montrons en utilisant le fait que\( a_n=|a_n\) ou\( a_n=−|a_n|\) et donc\( |a_n|+a_n=2|a_n|\) ou\( |a_n|+a_n=0\). Par conséquent,\( 0≤|a_n|+a_n≤2|a_n|\). Par conséquent, par le test de comparaison, puisque\( 2\sum^∞_{n=1}|a_n|\) converge, la série
\[\sum_{n=1}^∞(|a_n|+a_n) \nonumber \]
converge. En utilisant les propriétés algébriques des séries convergentes, nous concluons que
\[\sum_{n=1}^∞a_n=\sum_{n=1}^∞(|a_n|+a_n)−\sum_{n=1}^∞|a_n| \nonumber \]
converge.
□
Pour chacune des séries suivantes, déterminez si la série converge de manière absolue, converge de manière conditionnelle ou diverge.
- \(\displaystyle \sum^∞_{n=1}\frac{(−1)^{n+1}}{3n+1}\)
- \(\displaystyle \sum^∞_{n=1}\frac{\cos(n)}{n^2}\)
Solution
a. Nous pouvons voir que
\(\displaystyle \sum_{n=1}^∞\left|\dfrac{(−1)^{n+1}}{3n+1}\right|=\sum_{n=1}^∞\dfrac{1}{3n+1}\)
diverge en utilisant le test de comparaison des limites avec la série harmonique. En fait,
\(\displaystyle \lim_{n→∞}\dfrac{1/(3n+1)}{1/n}=\dfrac{1}{3}\).
Par conséquent, la série ne converge pas absolument. Cependant, puisque
\( \dfrac{1}{3(n+1)+1}<\dfrac{1}{3n+1}\)et\( \dfrac{1}{3n+1}→0\),
la série converge. Nous pouvons en conclure que cela\(\displaystyle \sum^∞_{n=1}\frac{(−1)^{n+1}}{3n+1}\) converge de manière conditionnelle.
b. Notant que\( |\cos n|≤1,\) pour déterminer si la série converge de manière absolue, comparez
\(\displaystyle \sum_{n=1}^∞\left|\dfrac{\cos n}{n^2}\right|\)
avec la série\(\displaystyle \sum^∞_{n=1}\frac{1}{n^2}\). Puisque\(\displaystyle \sum^∞_{n=1}\frac{1}{n^2}\) converge, selon le test de comparaison,\(\displaystyle \sum^∞_{n=1}\left|\frac{\cos n}{n^2}\right|\) converge, et donc\(\displaystyle \sum^∞_{n=1}\frac{\cos n}{n^2}\) converge absolument.
Déterminez si la série\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\frac{n}{2n^3+1}\) converge de manière absolue, converge de manière conditionnelle ou diverge.
- Allusion
-
Vérifiez d'abord la convergence absolue.
- Réponse
-
La série converge absolument.
Pour voir la différence entre la convergence absolue et la convergence conditionnelle, regardez ce qui se passe lorsque nous réorganisons les termes des séries harmoniques alternées\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\frac{1}{n}\). Nous montrons que nous pouvons réorganiser les termes pour que la nouvelle série diverge. Il est certain que si nous réorganisons les termes d'une somme finie, la somme ne changera pas. Cependant, lorsque nous travaillons avec une somme infinie, des choses intéressantes peuvent se produire.
Commencez par ajouter suffisamment de termes positifs pour produire une somme plus grande qu'un nombre réel.\( M=10\) Par exemple, laissez\( M=10,\) et trouvez un entier\( k\) tel que
\[1+\dfrac{1}{3}+\dfrac{1}{5}+⋯+\dfrac{1}{2k−1}>10 \nonumber \]
(Nous pouvons le faire parce que la série\(\displaystyle \sum^∞_{n=1}\frac{1}{2n−1}\) diverge à l'infini.) Ensuite, soustrayez\( 1/2\). Ajoutez ensuite d'autres termes positifs jusqu'à ce que la somme atteigne 100. C'est-à-dire, trouvez un autre entier\( j>k\) tel que
\[(1+\dfrac{1}{3}+⋯+\dfrac{1}{2k−1}−\dfrac{1}{2}+\dfrac{1}{2k+1}+ \ldots +\dfrac{1}{2j+1}>100. \nonumber \]
Puis soustraire\( 1/4.\) En continuant ainsi, nous avons trouvé un moyen de réarranger les termes de la série harmonique alternée de telle sorte que la séquence des sommes partielles de la série réarrangée soit illimitée et diverge donc.
Les termes de la série harmonique alternée peuvent également être réarrangés de manière à ce que la nouvelle série converge vers une valeur différente. Dans Exemple, nous montrons comment réorganiser les termes pour créer une nouvelle série qui converge vers\( 3\ln(2)/2\). Nous soulignons que les séries harmoniques alternées peuvent être réarrangées pour créer une série qui converge vers n'importe quel nombre réel\( r\) ; cependant, la preuve de ce fait dépasse le cadre de ce texte.
En général, toute série\(\displaystyle \sum^∞_{n=1}a_n\) qui converge de manière conditionnelle peut être réorganisée de telle sorte que la nouvelle série diverge ou converge vers un nombre réel différent. Une série qui converge n'a absolument pas cette propriété. Pour toute série\(\displaystyle \sum^∞_{n=1}a_n\) qui converge de manière absolue, la valeur de\(\displaystyle \sum^∞_{n=1}a_n\) est la même pour tout réarrangement des termes. Ce résultat est connu sous le nom de théorème du réarrangement de Riemann, qui dépasse le cadre de ce livre.
Utilisez le fait que
\[ 1−\dfrac{1}{2}+\dfrac{1}{3}−\dfrac{1}{4}+\dfrac{1}{5}−⋯=\ln 2 \nonumber \]
pour réarranger les termes de la série harmonique alternée de telle sorte que la somme des séries réarrangées soit\( 3\ln (2)/2.\)
Solution
Laissez
\[ \sum_{n=1}^∞a_n=1−\dfrac{1}{2}+\dfrac{1}{3}−\dfrac{1}{4}+\dfrac{1}{5}−\dfrac{1}{6}+\dfrac{1}{7}−\dfrac{1}{8}+⋯. \nonumber \]
Puisque\(\displaystyle \sum_{n=1}^∞a_n=\ln (2)\), par les propriétés algébriques des séries convergentes,
\[ \sum_{n=1}^∞\dfrac{1}{2}a_n=\dfrac{1}{2}−\dfrac{1}{4}+\dfrac{1}{6}−\dfrac{1}{8}+⋯=\dfrac{1}{2}\sum_{n=1}^∞a_n=\dfrac{\ln 2}{2}. \nonumber \]
Maintenant, présentez la série de\(\displaystyle \sum_{n=1}^∞b_n\) telle sorte que pour tous\( n≥1, b_{2n−1}=0\) et\( b_{2n}=a_n/2.\) ensuite
\[ \sum_{n=1}^∞b_n=0+\dfrac{1}{2}+0−\dfrac{1}{4}+0+\dfrac{1}{6}+0−\dfrac{1}{8}+⋯=\dfrac{\ln 2}{2}. \nonumber \]
Ensuite, en utilisant les propriétés limites algébriques des séries convergentes, puisque\(\displaystyle \sum_{n=1}^∞a_n\) et\(\displaystyle \sum_{n=1}^∞b_n\) convergent, la série\(\displaystyle \sum_{n=1}^∞(a_n+b_n)\) converge et
\[ \sum_{n=1}^∞(a_n+b_n)=\sum_{n=1}^∞a_n+\sum_{n=1}^∞b_n=\ln 2+\dfrac{\ln 2}{2}=\dfrac{3\ln 2}{2}. \nonumber \]
Maintenant, ajoutez les termes correspondants\( b_n\),\( a_n\) et nous voyons que
\[ \sum_{n=1}^∞(a_n+b_n)=(1+0)+\left(−\dfrac{1}{2}+\dfrac{1}{2}\right)+\left(\dfrac{1}{3}+0\right)+\left(−\dfrac{1}{4}−14\right)+\left(\dfrac{1}{5}+0\right)+\left(−\dfrac{1}{6}+\dfrac{1}{6}\right)+\left(\dfrac{1}{7}+0\right)+\left(\dfrac{1}{8}−\dfrac{1}{8}\right)+⋯=1+\dfrac{1}{3}−\dfrac{1}{2}+\dfrac{1}{5}+\dfrac{1}{7}−\dfrac{1}{4}+⋯. \nonumber \]
Nous remarquons que la série sur le côté droit du signe égal est un réarrangement de la série harmonique alternée. Puisque\(\displaystyle \sum_{n=1}^∞(a_n+b_n)=3\ln (2)/2,\) nous concluons que
\[ 1+\dfrac{1}{3}−\dfrac{1}{2}+\dfrac{1}{5}+\dfrac{1}{7}−\dfrac{1}{4}+⋯=\dfrac{3\ln (2)}{2}. \nonumber \]
Nous avons donc trouvé un réarrangement des séries harmoniques alternées ayant la propriété souhaitée.
Concepts clés
- Pour une série alternée\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}b_n,\) si\( b_{k+1}≤b_k\) pour toutes\( k\) et\( b_k→0\) lorsque\( k→∞,\) la série alternée converge.
- Si\(\displaystyle \sum^∞_{n=1}|a_n|\) converge, puis\(\displaystyle \sum^∞_{n=1}a_n\) converge.
Équations clés
- Séries alternatives
\(\displaystyle \sum_{n=1}^∞(−1)^{n+1}b_n=b_1−b_2+b_3−b_4+⋯\)ou
\(\displaystyle \sum_{n=1}^∞(−1)^nb_n=−b_1+b_2−b_3+b_4−⋯\)
Lexique
- convergence absolue
- si la série\(\displaystyle \sum^∞_{n=1}|a_n|\) converge,\(\displaystyle \sum^∞_{n=1}a_n\) on dit que la série converge absolument
- séries alternées
- une série de la forme\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}b_n\) ou\(\displaystyle \sum^∞_{n=1}(−1)^nb_n\), où\( b_n≥0\), est appelée série alternée
- essai en série alternée
- pour une série alternée de l'une ou l'autre forme, si\( b_{n+1}≤b_n\) pour tous les entiers\( n≥1\) et\( b_n→0\), alors une série alternative converge
- convergence conditionnelle
- si la série\(\displaystyle \sum^∞_{n=1}a_n\) converge, mais que la série\(\displaystyle \sum^∞_{n=1}|a_n|\) diverge,\(\displaystyle \sum^∞_{n=1}a_n\) on dit que la série converge de manière conditionnelle


