9.5E : Exercices pour la section 9.5

Dans les exercices 1 à 30, indiquez si chacune des séries suivantes converge de manière absolue, conditionnelle ou pas du tout.

1)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\frac{n}{n+3}\)

2)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\frac{\sqrt{n}+1}{\sqrt{n}+3}\)

Réponse

Cette série diverge selon le test de divergence. Les termes n'ont pas tendance à être nuls.

3)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\frac{1}{\sqrt{n+3}}\)

4)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\frac{\sqrt{n+3}}{n}\)

Réponse

Converge conditionnellement par un test en série alterné, car\(\sqrt{n+3}/n\) il est décroissant et sa limite est 0. Ne converge pas absolument par rapport à la\(p\) série -,\(p=1/2\).

5)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\frac{1}{n!}\)

6)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\frac{3^n}{n!}\)

Réponse

Converge absolument par rapport aux limites, par\(3^n/4^n,\) exemple.

7)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\left(\frac{n−1}{n}\right)^n\)

8)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\left(\frac{n+1}{n}\right)^n\)

Réponse

Diverge par test de divergence depuis\(\displaystyle \lim_{n→∞}|a_n|=e\) et non\(0\).

9)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\sin^2n\)

10)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\cos^2n\)

Réponse

Diverge selon le test de divergence, puisque ses termes n'ont pas tendance à être nuls. La limite de la séquence de ses termes n'existe pas.

11)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\sin^2(1/n)\)

(12)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\cos^2(1/n)\)

Réponse

\(\displaystyle \lim_{n→∞}\cos^2(1/n)=1.\)Diverge par test de divergence.

13)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\ln(1/n)\)

(14)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\ln(1+\frac{1}{n})\)

Réponse

Converge par test en série alternée.

(15)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\frac{n^2}{1+n^4}\)

16)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\frac{n^e}{1+n^π}\)

Réponse

Converge conditionnellement par un test en série alterné. Ne converge pas absolument par comparaison des limites avec les\(p\) séries,\(p=π−e\)

Solution :

17)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}2^{1/n}\)

18)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}n^{1/n}\)

Réponse

Diverge ; les termes n'ont pas tendance à être nuls.

19)\(\displaystyle \sum^∞_{n=1}(−1)^n(1−n^{1/n})\) (Conseil :\(n^{1/n}≈1+\ln(n)/n\) pour les grands\(n\).)

20)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}n\left(1−\cos\left(\frac{1}{n}\right)\right)\) (Conseil :\(\cos(1/n)≈1−1/n^2\) pour les grands\(n\).)

Réponse

Converge par test en série alternée. Ne converge pas absolument par comparaison des limites avec les séries harmoniques.

21)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}(\sqrt{n+1}−\sqrt{n})\) (Conseil : rationalisez le numérateur.)

22)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\left(\frac{1}{\sqrt{n}}−\frac{1}{\sqrt{n+1}}\right)\) (Conseil : Multipliez puis rationalisez le numérateur.)

Réponse

Converge absolument par comparaison des limites avec\(p\) -series,\(p=3/2\), après avoir appliqué l'astuce.

23)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}(\ln(n+1)−\ln n)\)

24)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}n(\tan^{−1}(n+1)−\tan^{−1}n)\) (Conseil : utilisez le théorème de la valeur moyenne.)

Réponse

Converge par un test de série alterné puisque\( n(\tan^{−1}(n+1)−\tan^{−1}n)\) diminue jusqu'à zéro pour les grands\(n\). Ne converge pas absolument par comparaison des limites avec les séries harmoniques après application de l'indice.

25)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}((n+1)^2−n^2)\)

(26)\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\left(\frac{1}{n}−\frac{1}{n+1}\right)\)

Réponse

Converge absolument, puisque ce\( a_n=\dfrac{1}{n}−\dfrac{1}{n+1}\) sont des termes de série télescopique.

(27)\(\displaystyle \sum^∞_{n=1}\frac{\cos(nπ)}{n}\)

(28)\(\displaystyle \sum^∞_{n=1}\frac{\cos(nπ)}{n^{1/n}}\)

Réponse

Les termes n'ont pas tendance à être nuls. La série diverge par test de divergence.

(29)\(\displaystyle \sum^∞_{n=1}\frac{1}{n}\sin(\frac{nπ}{2})\)

(30)\(\displaystyle \sum^∞_{n=1}\sin(nπ/2)\sin(1/n)\)

Réponse

Converge par test en série alternée. Ne converge pas absolument par comparaison des limites avec les séries harmoniques.

Dans les exercices 31 à 36, utilisez l'estimation\(|R_N|≤b_{N+1}\) pour trouver une valeur\(N\) qui garantit que la somme des premiers\(N\) termes de la série alternée\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}b_n\) diffère de la somme infinie d'au plus l'erreur donnée. Calculez la somme partielle\(S_N\) pour cela\(N\).

31) [T]\(b_n=1/n,\) erreur\( <10^{−5}\)

32) [T]\(b_n=1/\ln(n), n≥2,\) erreur\(<10^{−1}\)

Réponse

\( \ln(N+1)>10, N+1>e^{10}, N≥22026; S_{22026}=0.0257…\)

33) [T]\(b_n=1/\sqrt{n},\) erreur\(<10^{−3}\)

34) [T]\(b_n=1/2^n\), erreur\(<10^{−6}\)

Réponse

\(2^{N+1}>10^6\)ou\(N+1>6\ln(10)/\ln(2)=19.93.\) ou\(N≥19; S_{19}=0.333333969…\)

35) [T]\(b_n=ln(1+\dfrac{1}{n}),\) erreur\( <10^{−3}\)

36) [T]\(b_n=1/n^2,\) erreur\(<10^{−6}\)

Réponse

\((N+1)^2>10^6\)ou\(N>999; S_{1000}≈0.822466.\)

Pour les exercices 37 à 45, indiquez si chacune des affirmations suivantes est vraie ou fausse. Si la déclaration est fausse, donnez un exemple dans lequel elle est fausse.

37) Il\( b_n≥0\) est décroissant puis\(\displaystyle \lim_{n→∞}b_n=0\)\(\displaystyle \sum_{n=1}^∞(b_{2n−1}−b_{2n})\) converge absolument.

38) Il\( b_n≥0\) est décroissant, alors\(\displaystyle \sum_{n=1}^∞(b_{2n−1}−b_{2n})\) converge absolument.

Réponse

C'est vrai. \(b_n\)il n'est pas nécessaire de tendre vers zéro puisque si\(\displaystyle c_n=b_n−\lim b_n\), alors\(c_{2n−1}−c_{2n}=b_{2n−1}−b_{2n}.\)

39) Si\( b_n≥0\) et\(\displaystyle \lim_{n→∞}b_n=0\) puis\(\displaystyle \sum_{n=1}^∞(\frac{1}{2}(b_{3n−2}+b_{3n−1})−b_{3n})\) converge.

40) Il\(b_n≥0\) est décroissant et\(\displaystyle \sum_{n=1}^∞(b_{3n−2}+b_{3n−1}−b_{3n})\) converge puis\(\displaystyle \sum_{n=1}^∞b_{3n−2}\) converge.

Réponse

C'est vrai. \(b_{3n−1}−b_{3n}≥0,\)la convergence de\(\displaystyle \sum b_{3n−2}\) suit donc le test de comparaison.

41) S'il\(b_n≥0\) est décroissant et\(\displaystyle \sum_{n=1}^∞(−1)^{n−1}b_n\) converge de manière conditionnelle mais pas absolument, il\(b_n\) ne tend pas vers zéro.

42) Laissez\(a^+_n=a_n\) si\(a_n≥0\) et\( a^−_n=−a_n\) si\(a_n<0\). (Aussi,\( a^+_n=0\) si\(a_n<0\) et\(a^−_n=0\) si\(a_n≥0\).) Si elle\(\displaystyle \sum_{n=1}^∞a_n\) converge de manière conditionnelle mais pas absolument, alors\(\displaystyle \sum_{n=1}^∞a^+_n\) ni ne\(\displaystyle \sum_{n=1}^∞a^−_n\) converge.

Réponse

C'est vrai. Si l'un converge, il en va de même pour l'autre, ce qui implique une convergence absolue.

43) Supposons qu'il\(a_n\) s'agisse d'une séquence de nombres réels positifs et qu'elle\(\displaystyle \sum_{n=1}^∞a_n\) converge.

44) Supposons qu'il\(b_n\) s'agisse d'une séquence arbitraire de un et d'un moins. \(\displaystyle \sum_{n=1}^∞a_nb_n\)Converge-t-il nécessairement ?

45) Supposons qu'\(a_n\)il s'agisse d'une séquence qui\(\displaystyle \sum_{n=1}^∞a_nb_n\) converge pour chaque séquence possible\(b_n\) de zéros et de uns. \(\displaystyle \sum_{n=1}^∞a_n\)Converge-t-il absolument ?

Réponse

Oui. Prends\(b_n=1\) si\(a_n≥0\) et\( b_n=0\) si\(a_n<0\). Puis\(\displaystyle \sum_{n=1}^∞a_nb_n=\sum_{n:a_n≥0}a_n\) converge. De même, on peut montrer\(\displaystyle \sum_{n:a_n<0}a_n\) des convergences. Puisque les deux séries convergent, les séries doivent absolument converger.

Dans les exercices 46 à 49, les séries ne répondent pas aux hypothèses du test des séries alternées comme indiqué. Dans chaque cas, indiquez quelle hypothèse n'est pas satisfaite. Indiquez si la série converge absolument.

46)\(\displaystyle \sum_{n=1}^∞(−1)^{n+1}\frac{\sin^2n}{n}\)

47)\(\displaystyle \sum_{n=1}^∞(−1)^{n+1}\frac{\cos^2n}{n}\)

Réponse

Non décroissant. Ne converge pas absolument.

48)\(\displaystyle 1+\frac{1}{2}−\frac{1}{3}−\frac{1}{4}+\frac{1}{5}+\frac{1}{6}−\frac{1}{7}−\frac{1}{8}+⋯\)

49)\(\displaystyle 1+\frac{1}{2}−\frac{1}{3}+\frac{1}{4}+\frac{1}{5}−\frac{1}{6}+\frac{1}{7}+\frac{1}{8}−\frac{1}{9}+⋯\)

Réponse

Pas en alternance. Peut être exprimé comme\(\displaystyle \sum_{n=1}^∞\left(\frac{1}{3n−2}+\frac{1}{3n−1}−\frac{1}{3n}\right),\) ce qui diverge par rapport à\(\displaystyle \sum_{n=1}^∞\frac{1}{3n−2}.\)

50) Montrez que les séries alternées\(\displaystyle 1−\frac{1}{2}+\frac{1}{2}−\frac{1}{4}+\frac{1}{3}−\frac{1}{6}+\frac{1}{4}−\frac{1}{8}+⋯\) ne convergent pas. Quelle hypothèse du test en série alternée n'est pas satisfaite ?

51) Supposons que cela\(\displaystyle \sum a_n\) converge absolument. Montrez que la série composée des termes positifs converge\(a_n\) également.

Réponse

Laissez\(a^+_n=a_n\) si\(a_n≥0\) et\(a^+_n=0\) si\( a_n<0\). Alors,\(a^+_n≤|a_n|\) pour tous\(n\), la séquence des sommes partielles de augmente et\( a^+_n\) est bornée au-dessus par la séquence des sommes partielles de\( |a_n|\), qui converge ; donc,\(\displaystyle \sum_{n=1}^∞a^+_n\) converge.

52) Montrez que les séries alternées\(\displaystyle \frac{2}{3}−\frac{3}{5}+\frac{4}{7}−\frac{5}{9}+⋯\) ne convergent pas. Quelle hypothèse du test en série alternée n'est pas satisfaite ?

53) La formule\(\displaystyle \cos θ=1−\frac{θ^2}{2!}+\frac{θ^4}{4!}−\frac{θ^6}{6!}+⋯\) sera dérivée dans le chapitre suivant. Utilisez le reste\(|R_N|≤b_{N+1}\) pour déterminer la limite de l'erreur lors de l'estimation\(\cos θ\) par la cinquième somme partielle\(1−θ^2/2!+θ^4/4!−θ^6/6!+θ^8/8!\) pour\(θ=1, θ=π/6,\) et\(θ=π.\)

Réponse

Car l'\(N=5\)un l'a fait\(∣R_N∣b_6=θ^{10}/10!\). Quand\(θ=1, R_5≤1/10!≈2.75×10^{−7}\). Quand\(θ=π/6,\)\(R_5≤(π/6)^{10}/10!≈4.26×10^{−10}\). Quand\(θ=π, R_5≤π^{10}/10!=0.0258.\)

54) La formule\(\sin θ=θ−\dfrac{θ^3}{3!}+\dfrac{θ^5}{5!}−\dfrac{θ^7}{7!}+⋯\) sera dérivée dans le chapitre suivant. Utilisez le reste\(|R_N|≤b_{N+1}\) pour déterminer la limite de l'erreur lors de l'estimation\(\sin θ\) par la cinquième somme partielle\(θ−θ^3/3!+θ^5/5!−θ^7/7!+θ^9/9!\) pour\(θ=1, θ=π/6,\) et\(θ=π.\)

55) Combien de termes\(\cos θ=1−\dfrac{θ^2}{2!}+\dfrac{θ^4}{4!}−\dfrac{θ^6}{6!}+⋯\) sont nécessaires pour obtenir une\(\cos 1\) précision approximative d'au plus une erreur\( 0.00001\) ?

Réponse

Laissez\( b_n=1/(2n−2)!.\) alors\(R_N≤1/(2N)!<0.00001\) quand\((2N)!>10^5\) ou\(N=5\) et\(\displaystyle 1−\frac{1}{2!}+\frac{1}{4!}−\frac{1}{6!}+\frac{1}{8!}=0.540325…\), tandis que\(\cos 1=0.5403023…\)

56) Combien de termes\(\sin θ=θ−\dfrac{θ^3}{3!}+\dfrac{θ^5}{5!}−\dfrac{θ^7}{7!}+⋯\) sont nécessaires pour obtenir une\(\sin 1\) précision approximative d'au plus une erreur\(0.00001?\)

57) Parfois, la série alternative\(\displaystyle \sum_{n=1}^∞(−1)^{n−1}b_n\) converge vers une certaine fraction d'une série absolument convergente\(\displaystyle \sum_{n=1}^∞b_n\) à un rythme plus rapide. Compte tenu de cela\(\displaystyle \sum_{n=1}^∞\frac{1}{n^2}=\frac{π^2}{6}\), trouvez\(\displaystyle S=1−\frac{1}{2^2}+\frac{1}{3^2}−\frac{1}{4^2}+⋯\). Laquelle de ces séries\(\displaystyle 6\sum_{n=1}^∞\frac{1}{n^2}\)\(\displaystyle S\sum_{n=1}^∞\frac{(−1)^{n−1}}{n^2}\) donne une meilleure estimation de l'\(π^2\)utilisation des\(1000\) termes ?

Réponse

Laissez\(\displaystyle T=\sum\frac{1}{n^2}.\)\(T−S=\dfrac{1}{2}T\) Then, donc\(S=T/2\). \(\displaystyle \sqrt{6×\sum_{n=1}^{1000}1/n^2}=3.140638…; \sqrt{\frac{1}{2}×\sum_{n=1}^{1000}(−1)^{n−1}/n^2}=3.141591…; π=3.141592….\)La série alternée est plus précise pour les\(1000\) termes.

Les séries alternées des exercices 58 et 59 convergent vers des multiples donnés de\(π\). Déterminez la valeur de l'estimation\(N\) prévue par le reste de l'estimation de telle sorte que la somme\(N^{\text{th}}\) partielle de la série se rapproche avec précision du côté gauche, dans les limites de l'erreur donnée. Déterminez le minimum\(N\) pour lequel la borne d'erreur s'applique et donnez la valeur approximative souhaitée dans chaque cas. Jusqu'à\(15\) des décimales,\( π=3.141592653589793….\)

58) [T]\(\displaystyle \frac{π}{4}=\sum_{n=0}^∞\frac{(−1)^n}{2n+1},\) erreur\(<0.0001\)

59) [T]\(\displaystyle \frac{π}{\sqrt{12}}=\sum_{k=0}^∞\frac{(−3)^{−k}}{2k+1},\) erreur\(<0.0001\)

Réponse

\(N=6, S_N=0.9068\)

60) [T] La série\(\displaystyle \sum_{n=0}^∞\frac{\sin(x+πn)}{x+πn}\) joue un rôle important dans le traitement du signal. Montre qui\(\displaystyle \sum_{n=0}^∞\frac{\sin(x+πn)}{x+πn}\) converge à tout moment\(0<x<π\). (Conseil : utilisez la formule pour le sinus d'une somme d'angles.)

61) [T] Si\(\displaystyle \sum_{n=1}^N(−1)^{n−1}\frac{1}{n}→ln2,\) ce qui est\(\displaystyle 1+\frac{1}{3}+\frac{1}{5}−\frac{1}{2}−\frac{1}{4}−\frac{1}{6}+\frac{1}{7}+\frac{1}{9}+\frac{1}{11}−\frac{1}{8}−\frac{1}{10}−\frac{1}{12}+⋯?\)

Réponse

\(\ln(2).\)La somme\(n^{\text{th}}\) partielle est la même que celle des séries harmoniques alternées.

62) [T] Tracez la série\(\displaystyle \sum_{n=1}^{100}\frac{\cos(2πnx)}{n}\) pour\(0≤x<1\). Expliquez pourquoi\(\displaystyle \sum_{n=1}^{100}\frac{\cos(2πnx)}{n}\) diverge quand\(x=0,1\). Comment se comporte la série pour les autres\(x\) ?

63) [T] Tracez\(\displaystyle \sum_{n=1}^{100}\frac{\sin(2πnx)}{n}\) la série\(0≤x<1\) et commentez son comportement

Réponse

La série passe rapidement à proximité des points de terminaison. En\(x\) dehors des points de terminaison, le graphique ressemble à\( π(1/2−x)\).

64) [T] Tracez la série\(\displaystyle \sum_{n=1}^{100}\frac{\cos(2πnx)}{n^2}\) pour\( 0≤x<1\) et décrivez son graphique.

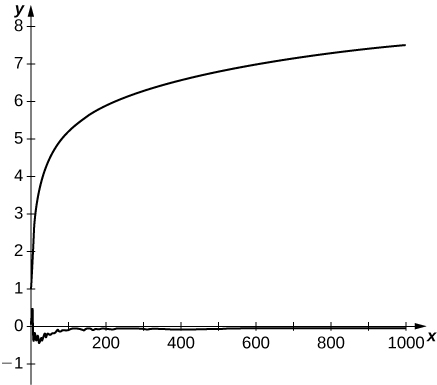
65) [T] La série harmonique alternée converge en raison de l'annulation de ses termes. Sa somme est connue car l'annulation peut être décrite de manière explicite. Une série harmonique aléatoire est l'une des formes\(\displaystyle \sum_{n=1}^∞\frac{S_n}{n}\), où se\(s_n\) trouve une séquence générée aléatoirement\(±1's\) dans laquelle les valeurs\(±1\) sont également susceptibles de se produire. Utilisez un générateur de nombres aléatoires pour produire des\(1000\) nombres aléatoires\(±1's\) et tracez les sommes partielles\(\displaystyle S_N=\sum_{n=1}^N\frac{s_n}{n}\) de votre séquence harmonique aléatoire\(N=1\) pour\(1000\). Comparez à un diagramme des premières sommes\(1000\) partielles de la série harmonique.

Réponse

Voici un résultat typique. La courbe supérieure est constituée de sommes partielles des séries harmoniques. La courbe inférieure représente les sommes partielles d'une série harmonique aléatoire.

66) [T] Les estimations de\(\displaystyle \sum_{n=1}^∞\frac{1}{n^2}\) peuvent être accélérées en écrivant ses sommes partielles au fur\(\displaystyle \sum_{n=1}^N\frac{1}{n^2}=\sum_{n=1}^N\frac{1}{n(n+1)}+\sum_{n=1}^N\frac{1}{n^2(n+1)}\) et à mesure et en rappelant que cela\(\displaystyle \sum_{n=1}^N\frac{1}{n(n+1)}=1−\frac{1}{N+1}\) converge vers une seule, comme\( N→∞.\) Comparez l'estimation de\(π^2/6\) l'utilisation des sommes\(\displaystyle \sum_{n=1}^{1000}\frac{1}{n^2}\) avec l'estimation en utilisant\(\displaystyle 1+\sum_{n=1}^{1000}\frac{1}{n^2(n+1)}\).

67) [T] La transformée d'Euler se réécrit\(\displaystyle S=\sum_{n=0}^∞(−1)^nb_n\) comme\(\displaystyle S=\sum_{n=0}^∞(−1)^n2^{−n−1}\sum_{m=0}^n(^n_m)b_{n−m}\). Pour les séries harmoniques alternées, elle prend la forme\(\displaystyle \ln(2)=\sum_{n=1}^∞\frac{(−1)^{n−1}}{n}=\sum_{n=1}^∞\frac{1}{n2^n}\). Calculez des sommes partielles\(\displaystyle \sum_{n=1}^∞\frac{1}{n2^n}\) jusqu'à ce qu'elles\(\ln(2)\) soient approximativement précises\(0.0001\). Combien de termes sont nécessaires ? Comparez cette réponse au nombre de termes des séries harmoniques alternées nécessaires pour effectuer une estimation\(\ln(2)\).

Réponse

Selon le test des séries alternées, on a\(|S_n−S|≤b_{n+1},\) donc besoin de\(10^4\) termes de la série harmonique alternative pour effectuer une estimation\(\ln(2)\) à l'intérieur\(0.0001\). Les premières sommes\(10\) partielles de la série\(\displaystyle \sum_{n=1}^∞\frac{1}{n2^n}\) sont (jusqu'à quatre décimales)\( 0.5000,0.6250,0.6667,0.6823,0.6885,0.6911,0.6923,0.6928,0.6930,0.6931\) et la dixième somme partielle se situe\(0.0001\) entre\(\ln(2)=0.6931….\)

68) [T] Dans le texte, il a été indiqué qu'une série convergente conditionnellement peut être réorganisée pour converger vers n'importe quel nombre. Voici un fait légèrement plus simple mais similaire. Si\(a_n≥0\) est\(a_n→0\) tel que\(n→∞\) mais\(\displaystyle \sum_{n=1}^∞a_n\) diverge, alors, pour n'importe quel nombre,\(A\) il existe une séquence\(s_n\)\( ±1's\) telle que\(\displaystyle \sum_{n=1}^∞a_ns_n→A.\) Afficher ceci pour la\(A>0\) manière suivante.

a. Définissez de manière récursive\(s_n\) par\( s_n=1\) if\(\displaystyle S_{n−1}=\sum_{k=1}^{n−1}a_ks_k<A\) et\( s_n=−1\) sinon.

b. Expliquez pourquoi, éventuellement\(S_n≥A,\) et pour tout ce qui est\(m\) plus grand que cela\(n\),\(A−a_m≤S_m≤A+a_m\).

c. Expliquez pourquoi cela implique\( S_n→A\) que\( n→∞.\)