9.2 : Série Infinite
- Page ID
- 197709
- Expliquez la signification de la somme d'une série infinie.
- Calculez la somme d'une série géométrique.
- Évaluez une série télescopique.
Nous avons vu qu'une séquence est un ensemble ordonné de termes. Si vous additionnez ces termes, vous obtenez une série. Dans cette section, nous définissons une série infinie et montrons comment les séries sont liées aux séquences. Nous définissons également ce que signifie la convergence ou la divergence d'une série. Nous présentons l'un des types de séries les plus importants : les séries géométriques. Nous utiliserons des séries géométriques dans le chapitre suivant pour écrire certaines fonctions sous forme de polynômes avec un nombre infini de termes. Ce processus est important car il nous permet d'évaluer, de différencier et d'intégrer des fonctions complexes en utilisant des polynômes plus faciles à manipuler. Nous discutons également de la série harmonique, sans doute la série divergente la plus intéressante car elle ne parvient tout simplement pas à converger.
Sommes et séries
Une série infinie est la somme d'une infinité de termes et s'écrit sous la forme
\(\displaystyle \sum_{n=1}^∞a_n=a_1+a_2+a_3+⋯.\)
Mais qu'est-ce que cela signifie ? Nous ne pouvons pas ajouter un nombre infini de termes de la même manière que nous pouvons ajouter un nombre fini de termes. La valeur d'une série infinie est plutôt définie en termes de limite des sommes partielles. La somme partielle d'une série infinie est une somme finie de la forme
\(\displaystyle \sum_{n=1}^ka_n=a_1+a_2+a_3+⋯+a_k.\)
Pour voir comment nous utilisons des sommes partielles pour évaluer des séries infinies, considérez l'exemple suivant. Supposons que du pétrole s'infiltre dans un lac de telle sorte que des\( 1000\) gallons entrent dans le lac la première semaine. Au cours de la deuxième semaine, des\( 500\) gallons de pétrole supplémentaires pénètrent dans le lac. La troisième semaine,\( 250\) plus de gallons entrent dans le lac. Supposons que cette tendance se poursuive de telle sorte que chaque semaine, la moitié du pétrole entre dans le lac par rapport à la semaine précédente. Si cela continue pour toujours, que pouvons-nous dire de la quantité de pétrole dans le lac ? La quantité de pétrole continuera-t-elle à augmenter arbitrairement, ou est-il possible qu'elle approche d'une quantité limitée ? Pour répondre à cette question, nous examinons la quantité de pétrole dans le lac après des\( k\) semaines. Si\( S_k\) l'on fait référence à la quantité de pétrole dans le lac (mesurée en milliers de gallons) après des\( k\) semaines, on constate que
\( S_1=1\)
\( S_2=1+0.5=1+\frac{1}{2}\)
\( S_3=1+0.5+0.25=1+\frac{1}{2}+\frac{1}{4}\)
\( S_4=1+0.5+0.25+0.125=1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}\)
\( S_5=1+0.5+0.25+0.125+0.0625=1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}.\)
En regardant ce schéma, nous constatons que la quantité de pétrole dans le lac (en milliers de gallons) après des\( k\) semaines est
\[ S_k=1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+⋯+\frac{1}{2^{k−1}}=\sum_{n=1}^k\left(\frac{1}{2}\right)^{n−1}. \nonumber \]
Nous nous intéressons à ce qui se passe de manière aussi\( k→∞.\) symbolique, à la quantité de pétrole dans le lac que\( k→∞\) celle donnée par la série infinie
\[\sum_{n=1}^∞\left(\frac{1}{2}\right)^{n−1}=1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+⋯. \nonumber \]
Dans le même temps\( k→∞\), la quantité de pétrole dans le lac peut être calculée en évaluant\(\displaystyle \lim_{k→∞}S_k\). Par conséquent, le comportement de la série infinie peut être déterminé en examinant le comportement de la séquence de sommes partielles\( {S_k}\). Si la séquence de sommes partielles\( {S_k}\) converge, on dit que la série infinie converge et que sa somme est donnée par\(\displaystyle \lim_{k→∞}S_k\). Si la séquence\( {S_k}\) diverge, on dit que la série infinie diverge. Nous allons maintenant nous concentrer sur la détermination de la limite de cette séquence\( {S_k}\).
Tout d'abord, en simplifiant certaines de ces sommes partielles, nous voyons que
\( S_1=1\)
\( S_2=1+\frac{1}{2}=\frac{3}{2}\)
\( S_3=1+\frac{1}{2}+\frac{1}{4}=\frac{7}{4}\)
\( S_4=1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}=\frac{15}{8}\)
\( S_5=1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}=\frac{31}{16}.\)
En traçant certaines de ces valeurs dans la figure, il semble que la séquence\( {S_k}\) pourrait se rapprocher de 2.
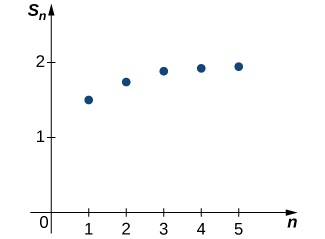
Cherchons des preuves plus convaincantes. Dans le tableau suivant, nous listons les valeurs de\(S_k\) pour plusieurs valeurs de\(k\).
| \( k\) | 5 | 10 | 15 | 20 |
|---|---|---|---|---|
| \( S_k\) | 1,9375 | 1 998 | 1,999939 | 1,999998 |
Ces données fournissent des preuves supplémentaires suggérant que la séquence\({S_k}\) converge vers\(2\). Plus tard, nous fournirons un argument analytique qui pourra être utilisé pour le prouver\(\displaystyle \lim_{k→∞}S_k=2\). Pour l'instant, nous nous appuyons sur les données numériques et graphiques pour nous convaincre que la séquence des sommes partielles converge réellement vers\(2\). Puisque cette séquence de sommes partielles converge vers\(2\), nous disons que la série infinie converge vers\(2\) et écrit
\[ \sum_{n=1}^∞\left(\frac{1}{2}\right)^{n−1}=2.\nonumber \]
Pour en revenir à la question sur le pétrole dans le lac, étant donné que cette série infinie converge vers\(2\), nous concluons que la quantité de pétrole dans le lac atteindra arbitrairement des\(2000\) gallons à mesure que le temps deviendra suffisamment important.
Cette série est un exemple de série géométrique. Nous aborderons les séries géométriques plus en détail plus loin dans cette section. Tout d'abord, nous résumons ce que signifie la convergence d'une série infinie.
Une série infinie est une expression de la forme
\[\sum_{n=1}^∞a_n=a_1+a_2+a_3+⋯. \nonumber \]
Pour chaque entier positif\(k\), la somme
\[S_k=\sum_{n=1}^ka_n=a_1+a_2+a_3+⋯+a_k \nonumber \]
est appelée la somme\(k^{\text{th}}\) partielle de la série infinie. Les sommes partielles forment une séquence\({S_k}\). Si la séquence de sommes partielles converge vers un nombre réel\(S\), la série infinie converge. Si nous pouvons décrire la convergence d'une série en\(S\), nous appelons\(S\) la somme de la série, et nous écrivons
\[\sum_{n=1}^∞a_n=S. \nonumber \]
Si la séquence des sommes partielles diverge, nous avons la divergence d'une série.
Notez que l'indice d'une série ne doit pas nécessairement commencer par n'importe quelle valeur\(n=1\) mais peut commencer par n'importe quelle valeur. Par exemple, la série
\[\sum_{n=1}^∞\left(\frac{1}{2}\right)^{n−1} \nonumber \]
peut également être écrit comme
\[\sum_{n=0}^∞\left(\frac{1}{2}\right)^n\; \text{or}\; \sum_{n=5}^∞\left(\frac{1}{2}\right)^{n−5}. \nonumber \]
Il est souvent pratique que l'indice commence à une valeur différente\(1\), donc si, pour une raison quelconque, il commence à une valeur différente, nous pouvons le réindexer en modifiant les variables. Par exemple, considérez la série
\[ \sum_{n=2}^∞\frac{1}{n^2}. \nonumber \]
En introduisant la variable\(m=n−1\), afin que\(n=m+1,\) nous puissions réécrire la série comme
\[ \sum_{m=1}^∞\frac{1}{(m+1)^2}. \nonumber \]
Pour chacune des séries suivantes, utilisez la séquence de sommes partielles afin de déterminer si la série converge ou diverge.
- \(\displaystyle \sum_{n=1}^∞\frac{n}{n+1}\)
- \(\displaystyle \sum_{n=1}^∞(−1)^n\)
- \(\displaystyle \sum_{n=1}^∞\frac{1}{n(n+1)}\)
Solution
a. La séquence de sommes partielles\({S_k}\) satisfait
\(S_1=\dfrac{1}{2}\)
\(S_2=\dfrac{1}{2}+\dfrac{2}{3}\)
\(S_3=\dfrac{1}{2}+\dfrac{2}{3}+\dfrac{3}{4}\)
\(S_4=\dfrac{1}{2}+\dfrac{2}{3}+\dfrac{3}{4}+\dfrac{4}{5}\).
Notez que chaque terme ajouté est supérieur à\(1/2\). Par conséquent, nous constatons que
\(S_1=\dfrac{1}{2}\)
\(S_2=\dfrac{1}{2}+\dfrac{2}{3}>\dfrac{1}{2}+\dfrac{1}{2}=2\left(\dfrac{1}{2}\right)\)
\(S_3=\dfrac{1}{2}+\dfrac{2}{3}+\dfrac{3}{4}>\dfrac{1}{2}+\dfrac{1}{2}+\dfrac{1}{2}=3\left(\dfrac{1}{2}\right)\)
\(S_4=\dfrac{1}{2}+\dfrac{2}{3}+\dfrac{3}{4}+\dfrac{4}{5}>\dfrac{1}{2}+\dfrac{1}{2}+\dfrac{1}{2}+\dfrac{1}{2}=4\left(\dfrac{1}{2}\right).\)
À partir de ce modèle, nous pouvons le voir\(S_k>k\left(\frac{1}{2}\right)\) pour chaque entier\(k\). Par conséquent,\({S_k}\) est illimité et, par conséquent, diverge. Par conséquent, la série infinie\(\displaystyle \sum^∞_{n=1}\frac{n}{n+1}\) diverge.
b. La séquence de sommes partielles\({S_k}\) satisfait
\(S_1=−1\)
\(S_2=−1+1=0\)
\(S_3=−1+1−1=−1\)
\(S_4=−1+1−1+1=0.\)
À partir de ce schéma, nous pouvons voir que la séquence des sommes partielles est
\[{S_k}={−1,0,−1,0,…}. \nonumber \]
Comme cette séquence diverge, la série infinie\(\displaystyle \sum^∞_{n=1}(−1)^n\) diverge.
c. La séquence de sommes partielles\( {S_k}\) satisfait
\( S_1=\dfrac{1}{1⋅2}=\dfrac{1}{2}\)
\( S_2=\dfrac{1}{1⋅2}+\dfrac{1}{2⋅3}=\dfrac{1}{2}+\dfrac{1}{6}=\dfrac{2}{3}\)
\( S_3=\dfrac{1}{1⋅2}+\dfrac{1}{2⋅3}+\dfrac{1}{3⋅4}=\dfrac{1}{2}+\dfrac{1}{6}+\dfrac{1}{12}=\dfrac{3}{4}\)
\( S_4=\dfrac{1}{1⋅2}+\dfrac{1}{2⋅3}+\dfrac{1}{3⋅4}+\dfrac{1}{4⋅5}=\dfrac{4}{5}\)
\( S_5=\dfrac{1}{1⋅2}+\dfrac{1}{2⋅3}+\dfrac{1}{3⋅4}+\dfrac{1}{4⋅5}+\dfrac{1}{5⋅6}=\dfrac{5}{6}.\)
À partir de ce schéma, nous pouvons voir que la somme\( k^{\text{th}}\) partielle est donnée par la formule explicite
\[ S_k=\frac{k}{k+1} \nonumber \].
Puisque\( k/(k+1)→1,\) nous concluons que la séquence de sommes partielles converge et que, par conséquent, la série infinie converge vers\( 1\). Nous avons
\[ \sum_{n=1}^∞\frac{1}{n(n+1)}=1. \nonumber \]
Déterminez si la série\(\displaystyle \sum^∞_{n=1}\frac{n+1}{n}\) converge ou diverge.
- Allusion
-
Regardez la séquence des sommes partielles.
- Réponse
-
La série diverge à cause de la somme\( k^{\text{th}}\) partielle\( S_k>k\).
La série Harmonic
Une série utile à connaître est la série harmonique. La série harmonique est définie comme
\[\sum_{n=1}^∞\frac{1}{n}=1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+⋯. \nonumber \]
Cette série est intéressante car elle diverge, mais elle diverge très lentement. Nous entendons par là que les termes de la séquence de sommes partielles se\( {S_k}\) rapprochent de l'infini, mais qu'ils le font très lentement. Nous allons montrer que la série diverge, mais nous illustrons d'abord la lente croissance des termes dans la séquence\( {S_k}\) dans le tableau suivant.
| \( k\) | 10 | 100 | 1000 | 10,00 | 100 000 | 1 000 000 |
|---|---|---|---|---|---|---|
| \( S_k\) | 2.92897 | 5. 18738 | 7,48 547 | 9,78 761 | 12.09015 | 14 39 273 |
Même après\( 1,000,000\) les trimestres, la somme partielle reste relativement faible. D'après ce tableau, il n'est pas clair que cette série diverge réellement. Cependant, nous pouvons montrer analytiquement que la séquence des sommes partielles diverge, et donc que la série diverge.
Pour montrer que la séquence des sommes partielles diverge, nous montrons que la séquence des sommes partielles est illimitée. Nous commençons par écrire les quelques premières sommes partielles :
\( S_1=1\)
\( S_2=1+\dfrac{1}{2}\)
\( S_3=1+\dfrac{1}{2}+\dfrac{1}{3}\)
\( S_4=1+\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}\).
Notez que pour les deux derniers trimestres de\( S_4\),
\[ \frac{1}{3}+\frac{1}{4}>\frac{1}{4}+\frac{1}{4} \nonumber \]
Par conséquent, nous concluons que
\[ S_4>1+\frac{1}{2}+\left(\frac{1}{4}+\frac{1}{4}\right)=1+\frac{1}{2}+\frac{1}{2}=1+2\left(\frac{1}{2}\right). \nonumber \]
En utilisant la même idée pour\( S_8\), nous voyons que
\(\displaystyle S_8=1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+\frac{1}{6}+\frac{1}{7}+\frac{1}{8}>1+\frac{1}{2}+\left(\frac{1}{4}+\frac{1}{4}\right)+\left(\frac{1}{8}+\frac{1}{8}+\frac{1}{8}+\frac{1}{8}\right)=1+\frac{1}{2}+\frac{1}{2}+\frac{1}{2}=1+3\left(\frac{1}{2}\right)\).
À partir de ce schéma, nous voyons que\( S_1=1, S_2=1+1/2, S_4>1+2(1/2),\) et\( S_8>1+3(1/2)\). Plus généralement, on peut le démontrer\( S_{2^j}>1+j(1/2)\) pour tous\( j>1\). Puisque\( 1+j(1/2)→∞,\) nous concluons que la séquence\( {S_k}\) est illimitée et qu'elle diverge donc. Dans la section précédente, nous avons indiqué que les séquences convergentes sont bornées. Par conséquent, puisqu'elle\( {S_k}\) est illimitée, elle diverge. Ainsi, la série harmonique diverge.
Propriétés algébriques des séries convergentes
Puisque la somme d'une série infinie convergente est définie comme la limite d'une séquence, les propriétés algébriques des séries répertoriées ci-dessous découlent directement des propriétés algébriques des séquences.
\(\displaystyle \sum_{n=1}^∞ a_n\)Let and\(\displaystyle \sum_{n=1}^∞ b_n\) be des séries convergentes. Les propriétés algébriques suivantes sont alors valables.
i. La série\(\displaystyle \sum_{n=1}^∞(a_n+b_n)\) converge, et\(\displaystyle \sum^∞_{n=1}(a_n+b_n)=\sum^∞_{n=1}a_n+\sum^∞_{n=1}b_n.\) (règle de somme)
ii. La série\(\displaystyle \sum_{n=1}^∞(a_n−b_n)\) converge, et\(\displaystyle \sum^∞_{n=1}(a_n−b_n)=\sum^∞_{n=1}a_n−\sum^∞_{n=1}b_n.\) (Règle de différence)
iii. Pour tout nombre réel\( c\), la série\(\displaystyle \sum_{n=1}^∞ca_n\) converge, et\(\displaystyle \sum^∞_{n=1}ca_n=c\sum^∞_{n=1}a_n\). (Règle multiple constante)
Évaluer\(\displaystyle \sum_{n=1}^∞\left[\frac{3}{n(n+1)}+\left(\frac{1}{2}\right)^{n−2}\right].\)
Solution
Nous avons montré plus tôt que
\[ \sum_{n=1}^∞\frac{1}{n(n+1)} = 1 \nonumber \]
et
\[ \sum_{n=1}^∞\left(\frac{1}{2}\right)^{n−1}=2. \nonumber \]
Comme ces deux séries convergent, nous pouvons appliquer les propriétés de Note\(\PageIndex{1}\) pour évaluer
\[\sum_{n=1}^∞\left[\frac{3}{n(n+1)}+\left(\frac{1}{2}\right)^{n−2}\right]. \nonumber \]
À l'aide de la règle de somme, écrivez
\(\displaystyle \sum_{n=1}^∞\left[\frac{3}{n(n+1)}+\left(\frac{1}{2}\right)^{n−2}\right]=\sum_{n=1}^∞\frac{3}{n(n+1)}+\sum_{n=1}^∞\left(\frac{1}{2}\right)^{n−2}.\)
Ensuite, en utilisant la règle du multiple constant et les sommes ci-dessus, nous pouvons conclure que
\(\displaystyle \sum^∞_{n=1}\frac{3}{n(n+1)}+\sum^∞_{n=1}\left(\frac{1}{2}\right)^{n−2}=3\sum^∞_{n=1}\frac{1}{n(n+1)}+\left(\frac{1}{2}\right)^{−1}\sum^∞_{n=1}\left(\frac{1}{2}\right)^{n−1}=3(1)+\left(\frac{1}{2}\right)^{−1}(2)=3+2(2)=7.\)
Évaluer\(\displaystyle \sum^∞_{n=1}\frac{5}{2^{n−1}}\).
- Allusion
-
Réécrivez en tant que\(\displaystyle \sum^∞_{n=1}5\left(\frac{1}{2}\right)^{n−1}\).
- Réponse
-
10
Série géométrique
Une série géométrique est toute série que nous pouvons écrire sous la forme
\[ a+ar+ar^2+ar^3+⋯=\sum_{n=1}^∞ar^{n−1}. \nonumber \]
Comme le rapport entre chaque terme de cette série et le terme précédent est r, le nombre r est appelé ratio. Nous appelons a le terme initial car il s'agit du premier terme de la série. Par exemple, la série
\[\sum_{n=1}^∞\left(\frac{1}{2}\right)^{n−1}=1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+⋯ \nonumber \]
est une série géométrique avec un terme\( a=1\) et un ratio initiaux\( r=1/2\).
En général, à quel moment une série géométrique converge-t-elle ? Considérez la série géométrique
\[\sum_{n=1}^∞ar^{n−1} \nonumber \]
quand\( a>0\). Sa séquence de sommes partielles\( {S_k}\) est donnée par
\[S_k=\sum_{n=1}^kar^{n−1}=a+ar+ar^2+⋯+ar^{k−1}. \nonumber \]
Prenons le cas où,\( r=1.\) dans ce cas,
\[S_k=a+a(1)+a(1)^2+⋯+a(1)^{k−1}=ak. \nonumber \]
Depuis\( a>0\), nous connaissons le\( ak→∞\) nom de\( k→∞\). Par conséquent, la séquence de sommes partielles est illimitée et diverge donc. Par conséquent, la série infinie diverge pour\( r=1\). Pour\( r≠1\), pour trouver la limite de\( {S_k}\), multipliez l'équation par\( 1−r\). Ce faisant, nous constatons que
\[ (1−r)S_k=a(1−r)(1+r+r^2+r^3+⋯+r^{k−1})=a[(1+r+r^2+r^3+⋯+r^{k−1})−(r+r^2+r^3+⋯+r^k)]=a(1−r^k). \nonumber \]
Toutes les autres conditions sont annulées.
Par conséquent,
\( S_k=\dfrac{a(1−r^k)}{1−r}\)pour\( r≠1\).
D'après notre discussion dans la section précédente, nous savons que la séquence géométrique\( r^k→0\) si\( |r|<1\) et qui\( r^k\) diverge si\( |r|>1\) ou\( r=±1\). Par conséquent, pour\( |r|<1, S_k→\dfrac{a}{1−r}\) et nous avons
\[ \sum_{n=1}^∞ar^{n−1}=\frac{a}{1−r}\; \text{if}\; |r|<1. \nonumber \]
Il\( |r|≥1, S_k\) diverge, et donc
\[ \sum_{n=1}^∞ar^{n−1} \; \text{diverges if}\; |r|≥1. \nonumber \]
Une série géométrique est une série de la forme
\[\sum_{n=1}^∞ar^{n−1}=a+ar+ar^2+ar^3+⋯. \nonumber \]
Si\( |r|<1\), la série converge, et
\[\sum_{n=1}^∞ar^{n−1}=\frac{a}{1−r}\; \text{for}\; |r|<1. \nonumber \]
Si\( |r|≥1\), la série diverge.
Les séries géométriques apparaissent parfois sous des formes légèrement différentes. Par exemple, il arrive que l'indice commence à une valeur autre que\( n=1\) ou que l'exposant implique une expression linéaire pour\( n\) une valeur différente de\( n−1\). Tant que nous pouvons réécrire la série sous la forme donnée par l'équation, il s'agit d'une série géométrique. Par exemple, considérez la série
\[\sum_{n=0}^∞\left(\frac{2}{3}\right)^{n+2}. \nonumber \]
Pour voir qu'il s'agit d'une série géométrique, nous écrivons les premiers termes :
\(\displaystyle \sum_{n=0}^∞\left(\frac{2}{3}\right)^{n+2}=\left(\frac{2}{3}\right)^2+\left(\frac{2}{3}\right)^3+\left(\frac{2}{3}\right)^4+⋯=\frac{4}{9}+\frac{4}{9}⋅\left(\frac{2}{3}\right)+\frac{4}{9}⋅\left(\frac{2}{3}\right)^2+⋯.\)
Nous voyons que le terme initial est\( a=4/9\) et que le ratio est.\( r=2/3.\) Par conséquent, la série peut être écrite comme
\(\displaystyle \sum_{n=1}^∞\frac{4}{9}⋅\left(\frac{2}{3}\right)^{n−1}.\)
Depuis\( r=2/3<1\), cette série converge et sa somme est donnée par
\(\displaystyle \sum_{n=1}^∞\frac{4}{9}⋅\left(\frac{2}{3}\right)^{n−1}=\frac{4/9}{1−2/3}=\frac{4}{3}.\)
Déterminez si chacune des séries géométriques suivantes converge ou diverge et, si elle converge, trouvez sa somme.
- \(\displaystyle \sum^∞_{n=1}\frac{(−3)^{n+1}}{4^{n−1}}\)
- \(\displaystyle \sum^∞_{n=1}e^{2n}\)
Solution
a. Pour écrire les premiers termes de la série, nous avons
\[\begin{align*} \sum_{n=1}^∞\frac{(−3)^{n+1}}{4^{n−1}} &= \frac{(−3)^2}{4^0}+\frac{(−3)^3}{4}+\frac{(−3)^4}{4^2}+⋯ \\[4pt] &=(−3)^2+(−3)^2⋅\left(\frac{−3}{4}\right)+(−3)^2⋅\left(\frac{−3}{4}\right)^2+⋯ \\[4pt] &=9+9⋅\left(\frac{−3}{4}\right)+9⋅\left(\frac{−3}{4}\right)^2+⋯. \end{align*}\]
La durée initiale\( a=−3\) et le ratio\( r=−3/4\). Depuis\( |r|=3/4<1\), la série converge vers
\[ \frac{9}{1−(−3/4)}=\frac{9}{7/4}=\frac{36}{7}. \nonumber \]
b. Rédaction de cette série en tant que
\[ e^2\sum_{n=1}^∞(e^2)^{n−1} \nonumber \]
nous pouvons voir qu'il s'agit d'une série géométrique où,\( r=e^2>1.\) par conséquent, la série diverge.
Déterminez si la série\(\displaystyle \sum_{n=1}^∞\left(\frac{−2}{5}\right)^{n−1}\) converge ou diverge. S'il converge, trouvez sa somme.
- Allusion
-
\( r=−2/5\)
- Réponse
-
\( 5/7\)
Nous tournons maintenant notre attention vers une belle application des séries géométriques. Nous montrons comment ils peuvent être utilisés pour écrire des décimales répétées sous forme de fractions d'entiers.
Utilisez une série géométrique pour écrire\( 3.\bar{26}\) sous la forme d'une fraction d'entiers.
Solution
Depuis le\( 3.\bar{26}—=3.262626…,\) début, nous écrivons
\[\begin{align*} 3.262626… &= 3+\frac{26}{100}+\frac{26}{1000}+\frac{26}{100,000}+⋯ \\[4pt] &=3+\frac{26}{10^2}+\frac{26}{10^4}+\frac{26}{10^6}+⋯. \end{align*}\]
En ignorant le terme 3, le reste de cette expression est une série géométrique avec un terme\( a=26/10^2\) et un ratio initiaux.\( r=1/10^2.\) Par conséquent, la somme de cette série est
\[ \frac{26/10^2}{1−(1/10^2)}=\frac{26/10^2}{99/10^2}=\frac{26}{99}. \nonumber \]
Ainsi,
\( 3.262626…=3+\frac{26}{99}=\frac{323}{99}\).
Écrivez\( 5.2\bar{7}\) sous la forme d'une fraction d'entiers.
- Allusion
-
En exprimant ce nombre sous forme de série, trouvez une série géométrique avec un terme\( a=7/100\) et un ratio initiaux\( r=1/10\).
- Réponse
-
\( 475/90\)
Définissez une séquence de figures de\( \{F_n\}\) manière récursive comme suit (Figure\(\PageIndex{2}\)). \( F_0\)Soit un triangle équilatéral avec des côtés de longueur\( 1\). En\( n≥1\) effet,\( F_n\) soit la courbe créée en retirant le tiers médian de chaque côté\( F_{n−1}\) et en le remplaçant par un triangle équilatéral pointant vers l'extérieur. La figure limite\( n→∞\) est connue sous le nom de flocon de neige de Koch.
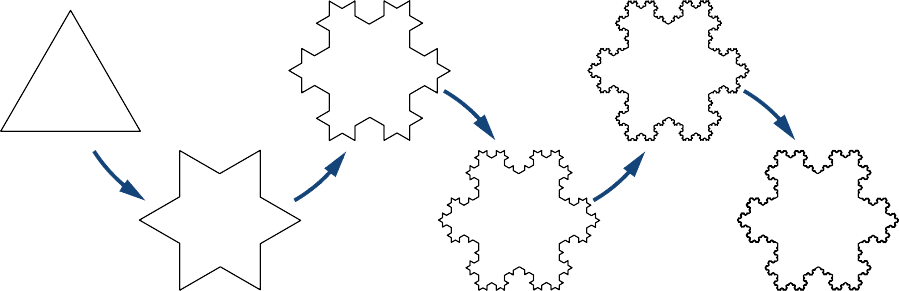
- Détermine la longueur\( L_n\) du périmètre de\( F_n\). Évaluez\(\displaystyle \lim_{n→∞}L_n\) pour déterminer la longueur du périmètre du flocon de neige de Koch.
- Trouvez la zone\( A_n\) de la figure\( F_n\). Évaluez\(\displaystyle \lim_{n→∞}A_n\) pour trouver la zone du flocon de neige de Koch.
Solution
a.\( N_n\) Soit le nombre de côtés de la figure\( F_n\). Puisque\( F_0\) c'est un triangle,\( N_0=3\). Soit la longueur de chaque côté de\( F_n\). Comme\( F_0\) il s'agit d'un triangle équilatéral avec des côtés de longueur\( l_0=1\), nous devons maintenant déterminer\( N_1\) et\( l_1\). Comme\( F_1\) est créé en retirant le tiers médian de chaque côté et en remplaçant ce segment de ligne par deux segments de ligne, pour chaque côté de\( F_0\), nous obtenons quatre côtés\( F_1\). Par conséquent, le nombre de côtés pour\( F_1\) est
\( N_1=4⋅3\).
Puisque la longueur de chacun de ces nouveaux segments de ligne est\( 1/3\) la longueur des segments de ligne dans\( F_0\), la longueur des segments de ligne pour\( F_1\) est donnée par
\( l_1=\frac{1}{3}⋅1=\frac{1}{3}\).
De même\( F_2\), puisque le tiers médian de chaque côté de\( F_1\) est retiré et remplacé par deux segments de ligne, le nombre de côtés\( F_2\) est donné par
\( N_2=4N_1=4(4⋅3)=4^2⋅3.\)
Puisque la longueur de chacun de ces côtés est\( 1/3\) la longueur des côtés de\( F_1\), la longueur de chaque côté de la figure\( F_2\) est donnée par
\( l_2=\frac{1}{3}⋅l_1=\frac{1}{3}⋅\frac{1}{3}=\left(\frac{1}{3}\right)^2\).
Plus généralement, puisqu'\( F_n\)il est créé en supprimant le tiers médian de chaque côté\( F_{n−1}\) et en remplaçant ce segment de ligne par deux segments de ligne de longueur\( \frac{1}{3}l_{n−1}\) en forme de triangle équilatéral, nous savons que\( N_n=4N_{n−1}\) et\( l_n=\dfrac{l_{n−1}}{3}\). Par conséquent, le nombre de côtés de la figure\( F_n\) est
\( N_n=4^n⋅3\)
et la longueur de chaque côté est
\[ l_n=\left(\frac{1}{3}\right)^n. \nonumber \]
Par conséquent, pour calculer le périmètre de\( F_n\), nous multiplions le nombre de côtés\( N_n\) et la longueur de chaque côté\( l_n\). Nous concluons que le périmètre de\( F_n\) est donné par
\[ L_n=N_n⋅l_n=3⋅\left(\frac{4}{3}\right)^n \nonumber \]
Par conséquent, la longueur du périmètre du flocon de neige de Koch est
\[ L=\lim_{n→∞}L_n=∞. \nonumber \]
b.\( T_n\) Dénotons l'aire de chaque nouveau triangle créé lors de la formation\( F_n\). Pour\( n=0, T_0\) est l'aire du triangle équilatéral d'origine. Par conséquent,\( T_0=A_0=\sqrt{3}/4\). \( n≥1\)En effet, puisque les longueurs des côtés du nouveau triangle sont\( 1/3\) celles des côtés de\( F_{n−1}\), nous avons
\[ T_n=\left(\frac{1}{3}\right)^2⋅T_{n−1}=\frac{1}{9}⋅T_{n−1}. \nonumber \]
Par conséquent,\( T_n=\left(\frac{1}{9}\right)^n⋅\frac{\sqrt{3}}{4}\). Comme un nouveau triangle se forme de chaque côté de\( F_{n−1}\),
\[ A_n=A_{n−1}+N_{n−1}⋅T_n=A_{n−1}+(3⋅4_{n−1})⋅\left(\frac{1}{9}\right)^n⋅\frac{\sqrt{3}}{4}=A_{n−1}+\frac{3}{4}⋅\left(\frac{4}{9}\right)^n⋅\frac{\sqrt{3}}{4}. \nonumber \]
En écrivant les premiers termes,\( A_0,A_1,A_2,\) nous voyons que
\( A_0=\frac{\sqrt{3}}{4}\)
\(A_1=A_0+\frac{3}{4}⋅\left(\frac{4}{9}\right)⋅\frac{\sqrt{3}}{4}=\frac{\sqrt{3}}{4}+\frac{3}{4}⋅\left(\frac{4}{9}\right)⋅\frac{\sqrt{3}}{4}=\frac{\sqrt{3}}{4}\left[1+\frac{3}{4}⋅\left(\frac{4}{9}\right)\right]\)
\( A_2=A_1+\frac{3}{4}⋅(\frac{4}{9})^2⋅\frac{\sqrt{3}}{4}=\frac{\sqrt{3}}{4}\left[1+\frac{3}{4}⋅\left(\frac{4}{9}\right)\right]+\frac{3}{4}⋅\left(\frac{4}{9}\right)^2⋅\frac{\sqrt{3}}{4}=\frac{\sqrt{3}}{4}[1+\frac{3}{4}⋅(\frac{4}{9})+\frac{3}{4}⋅\left(\frac{4}{9}\right)^2]\).
De manière plus générale,
\( A_n=\frac{\sqrt{3}}{4}\left[1+\frac{3}{4}\left(\frac{4}{9}+\left(\frac{4}{9}\right)^2+⋯+\left(\frac{4}{9}\right)^n\right)\right]\).
\( 4/9\)En tenant compte de chaque terme entre parenthèses intérieures, nous réécrivons notre expression comme
\( A_n=\frac{\sqrt{3}}{4}\left[1+\frac{1}{3}\left(1+\frac{4}{9}+\left(\frac{4}{9}\right)^2+⋯+\left(\frac{4}{9}\right)^{n−1}\right)\right]\).
L'expression\( 1+\left(\frac{4}{9}\right)+\left(\frac{4}{9}\right)^2+⋯+\left(\frac{4}{9}\right)^{n−1}\) est une somme géométrique. Comme indiqué précédemment, cette somme satisfait
\( 1+\frac{4}{9}+\left(\frac{4}{9}\right)^2+⋯+\left(\frac{4}{9}\right)^{n−1}=\dfrac{1−(4/9)^n}{1−(4/9)}.\)
En remplaçant cette expression par l'expression ci-dessus et en simplifiant, nous concluons que
\[ A_n=\frac{\sqrt{3}}{4}\left[1+\frac{1}{3}(\frac{1−(4/9)^n}{1−(4/9)})\right]=\frac{\sqrt{3}}{4}\left[\frac{8}{5}−\frac{3}{5}\left(\frac{4}{9}\right)^n\right]. \nonumber \]
Par conséquent, la zone du flocon de neige de Koch est
\(\displaystyle A=\lim_{n→∞}A_n=\frac{2\sqrt{3}}{5}.\)
Analyse
Le flocon de neige de Koch est intéressant car sa superficie est limitée et son périmètre est infini. Bien que cela puisse sembler impossible au début, rappelez-vous que vous avez vu des exemples similaires plus tôt dans le texte. Par exemple, considérez la région délimitée par la courbe\( y=1/x^2\) et l'\( x\)axe -sur l'intervalle\( [1,∞).\) Depuis l'intégrale incorrecte
\[ ∫^∞_1\frac{1}{x^2}\,dx \nonumber \]
converge, la superficie de cette région est limitée, même si le périmètre est infini.
Série télescopique
Considérez la série\(\displaystyle \sum_{n=1}^∞\frac{1}{n(n+1)}.\) Nous avons discuté de cette série dans Exemple, montrant que la série converge en écrivant les premières sommes partielles\( S_1,S_2,…,S_6\) et en remarquant qu'elles sont toutes de la forme\( S_k=\dfrac{k}{k+1}\). Nous utilisons ici une technique différente pour montrer que cette série converge. En utilisant des fractions partielles, on peut écrire
\[ \frac{1}{n(n+1)}=\frac{1}{n}−\frac{1}{n+1}. \nonumber \]
Par conséquent, la série peut être écrite comme
\(\displaystyle \sum_{n=1}^∞\left[\frac{1}{n}−\frac{1}{n+1}\right]=\left(1+\frac{1}{2}\right)+\left(\frac{1}{2}−\frac{1}{3}\right)+\left(\frac{1}{3}−\frac{1}{4}\right)+⋯.\)
En écrivant les premiers termes dans la séquence des sommes partielles,\( {S_k},\) nous voyons que
\( S_1=1−\frac{1}{2}\)
\( S_2=\left(1−\frac{1}{2}\right)+\left(\frac{1}{2}−\frac{1}{3}\right)=1−\frac{1}{3}\)
\( S_3=\left(1−\frac{1}{2}\right)+\left(\frac{1}{2}−\frac{1}{3}\right)+\left(\frac{1}{3}−\frac{1}{4}\right)=1−\frac{1}{4}\).
D'une manière générale,
\( S_k=\left(1−\frac{1}{2}\right)+\left(\frac{1}{2}−\frac{1}{3}\right)+\left(\frac{1}{3}−\frac{1}{4}\right)+⋯+\left(\frac{1}{k}−\frac{1}{k+1}\right)=1−\dfrac{1}{k+1}\).
Nous remarquons que les trimestres intermédiaires s'annulent mutuellement, ne laissant que le premier et le dernier trimestre. En un sens, la série s'effondre comme une longue-vue avec des tubes qui disparaissent les uns dans les autres pour raccourcir le télescope. Pour cette raison, nous appelons série télescopique une série possédant cette propriété. Pour cette série, depuis\( S_k=1−1/(k+1)\) et\( 1/(k+1)→0\) comme\( k→∞\), la séquence de sommes partielles converge vers\( 1\), et donc la série converge vers\( 1\).
Une série télescopique est une série dans laquelle la plupart des termes s'annulent dans chacune des sommes partielles, ne laissant que certains des premiers termes et certains des derniers termes.
Par exemple, n'importe quelle série du formulaire
\(\displaystyle \sum_{n=1}^∞[b_n−b_{n+1}]=(b_1−b_2)+(b_2−b_3)+(b_3−b_4)+⋯\)
est une série télescopique. Nous pouvons le constater en écrivant certaines des sommes partielles. En particulier, nous constatons que
\( S_1=b_1−b_2\)
\( S_2=(b_1−b_2)+(b_2−b_3)=b_1−b_3\)
\( S_3=(b_1−b_2)+(b_2−b_3)+(b_3−b_4)=b_1−b_4.\)
En général, la kième somme partielle de cette série est
\( S_k=b_1−b_{k+1}\).
Comme la kième somme partielle peut être simplifiée à la différence de ces deux termes, la séquence de sommes partielles\( {S_k}\) convergera si et seulement si la séquence\( {b_{k+1}}\) converge. De plus, si la séquence\( b_{k+1}\) converge vers un nombre fini B, alors la séquence de sommes partielles converge vers\( b_1−B\), et donc
\(\displaystyle \sum_{n=1}^∞[b_n−b_{n+1}]=b_1−B.\)
Dans l'exemple suivant, nous montrons comment utiliser ces idées pour analyser une série télescopique de cette forme.
Déterminez si la série télescopique
\(\displaystyle \sum_{n=1}^∞\left[\cos\left(\frac{1}{n}\right)−\cos\left(\frac{1}{n+1}\right)\right]\)
converge ou diverge. S'il converge, trouvez sa somme.
Solution
En écrivant les termes dans la séquence de sommes partielles, nous pouvons voir que
\( S_1=\cos(1)−\cos(\frac{1}{2})\)
\( S_2=(\cos(1)−\cos(\frac{1}{2}))+(\cos(\frac{1}{2})−\cos(\frac{1}{3}))=\cos(1)−\cos(\frac{1}{3})\)
\( S_3=(\cos(1)−\cos(\frac{1}{2}))+(\cos(\frac{1}{2})−\cos(\frac{1}{3}))+(\cos(\frac{1}{3})−\cos(\frac{1}{4}))\)
\( =\cos(1)−\cos(\frac{1}{4})\).
D'une manière générale,
\( S_k=\cos(1)−\cos\left(\frac{1}{k+1}\right)\).
\( 1/(k+1)→0\)Puisque\( k→∞\) et\( \cos x\) est une fonction continue,\( \cos(1/(k+1))→\cos(0)=1\). Nous concluons donc que\( S_k→\cos(1)−1\). La série télescopique converge et la somme est donnée par
\(\displaystyle \sum_{n=1}^∞\left[\cos\left(\frac{1}{n}\right)−\cos\left(\frac{1}{n+1}\right)\right]=\cos(1)−1.\)
Déterminez si elle\(\displaystyle \sum^∞_{n=1}[e^{1/n}−e^{1/(n+1)}]\) converge ou diverge. S'il converge, trouvez sa somme.
- Allusion
-
Écrivez la séquence des sommes partielles pour voir quels termes s'annulent.
- Réponse
-
\( e−1\)
Nous avons montré que les séries harmoniques\(\displaystyle \sum^∞_{n=1}\frac{1}{n}\) divergent. Nous étudions ici le comportement des sommes partielles.\( S_k\)\( k→∞.\) En particulier, nous montrons qu'elles se comportent comme la fonction logarithmique naturelle en montrant qu'il existe une constante\( γ\) telle que
\(\displaystyle \sum_{n=1}^k\left(\frac{1}{n}−\ln k\right)→γ\)comme\( k→∞.\)
Cette constante\( γ\) est connue sous le nom de constante d'Euler.
1. Laissez\(\displaystyle T_k=\sum_{n=1}^k\left(\frac{1}{n}−\ln k\right).\) Evaluer\( T_k\) pour différentes valeurs de\( k\).
2. Pour\( T_k\) tel que défini dans la partie 1, montrez que la séquence\( {T_k}\) converge en suivant les étapes suivantes.
a. Montrez que la séquence\( {T_k}\) est monotone décroissante. (Astuce : montrez que\( \ln(1+1/k>1/(k+1))\)
b. Montrez que la séquence\( {T_k}\) est limitée par zéro en dessous. (Conseil : Exprime\( \ln k\) sous forme d'intégrale définie.)
c. Utilisez le théorème de convergence monotone pour conclure que la séquence\( {T_k}\) converge. La limite\( γ\) est la constante d'Euler.
3. Estimez maintenant la\( T_k\) distance qui\( γ\) sépare un entier donné\( k\). \( k≥1, 0<T_k−γ≤1/k\)Prouvez-le en suivant les étapes suivantes.
a. Montrez que\( \ln(k+1)−\ln k<1/k.\)
b. Utilisez le résultat de la partie a. pour montrer que pour tout entier\( k\),
\[ T_k−T_{k+1}<\frac{1}{k}−\frac{1}{k+1}. \nonumber \]
c. Pour tous les entiers\( k\) et\( j\) tels que\( j>k\), exprimés\( T_k−T_j\) sous la forme d'une somme télescopique en écrivant
\[ T_k−T_j=(T_k−T_{k+1})+(T_{k+1}−T_{k+2})+(T_{k+2}−T_{k+3})+⋯+(T_{j−1}−T_j). \nonumber \]
Utilisez le résultat de la partie b. combiné à cette somme télescopique pour conclure que
\[ T_k−T_j<\frac{1}{k}−\frac{1}{j}. \nonumber \]
a. Appliquez la limite aux deux côtés de l'inégalité dans la partie c. pour conclure que
\[ T_k−γ≤\frac{1}{k}. \nonumber \]
e. Estimation\( γ\) avec une précision de 0,001 près.
Concepts clés
- Compte tenu de la série infinie
\(\displaystyle \sum_{n=1}^∞a_n=a_1+a_2+a_3+⋯\)
et la séquence correspondante de sommes partielles\( {S_k}\) où
\(\displaystyle S_k=\sum_{n=1}^ka_n=a_1+a_2+a_3+⋯+a_k\),
la série converge si et seulement si la séquence\( {S_k}\) converge.
- La série géométrique\(\displaystyle \sum^∞_{n=1}ar^{n−1}\) converge if\( |r|<1\) et diverge if\( |r|≥1.\) For\( |r|<1,\)
\(\displaystyle \sum_{n=1}^∞ar^{n−1}=\frac{a}{1−r}\).
- La série harmonique
\(\displaystyle \sum_{n=1}^∞\frac{1}{n}=1+\frac{1}{2}+\frac{1}{3}+⋯\)
diverge.
- Une série de la forme\(\displaystyle \sum_{n=1}^∞[b_n−b_{n+1}]=[b_1−b_2]+[b_2−b_3]+[b_3−b_4]+⋯+[b_n−b_{n+1}]+⋯\) est une série télescopique. La somme\( k^{\text{th}}\) partielle de cette série est donnée par\( S_k=b_1−b_{k+1}\). Les séries convergeront si et seulement si elles\(\displaystyle \lim_{k→∞} b_{k+1}\) existent. Dans ce cas,
\(\displaystyle \sum_{n=1}^∞[b_n−b_{n+1}]=b_1−\lim_{k→∞}(b_{k+1})\).
Équations clés
- Série Harmonic
\(\displaystyle \sum_{n=1}^∞\frac{1}{n}=1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+⋯\)
- Somme d'une série géométrique
\(\displaystyle \sum_{n=1}^∞ar^{n−1}=\frac{a}{1−r}\)pour\( |r|<1\)
Lexique
- convergence d'une série
- une série converge si la séquence de sommes partielles de cette série converge
- divergence d'une série
- une série diverge si la séquence de sommes partielles de cette série diverge
- série géométrique
- une série géométrique est une série qui peut être écrite sous la forme
\(\displaystyle \sum_{n=1}^∞ar^{n−1}=a+ar+ar^2+ar^3+⋯\)
- série harmonique
- la série harmonique prend la forme
\(\displaystyle \sum_{n=1}^∞\frac{1}{n}=1+\frac{1}{2}+\frac{1}{3}+⋯\)
- série infinie
- une série infinie est une expression de la forme
\(\displaystyle a_1+a_2+a_3+⋯=\sum_{n=1}^∞a_n\)
- somme partielle
-
la somme\( kth\) partielle de la série infinie\(\displaystyle \sum^∞_{n=1}a_n\) est la somme finie
\(\displaystyle S_k=\sum_{n=1}^ka_n=a_1+a_2+a_3+⋯+a_k\)
- série télescopique
- une série télescopique est une série dans laquelle la plupart des termes s'annulent dans chacune des sommes partielles


