9.1E : Exercices pour la section 9.1

Last updated
Save as PDF

Page ID: 197775

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Dans les exercices 1 à 4, trouvez les six premiers termes de chaque séquence, en commençant par$ n=1$.

1)$a_n=1+(−1)^n$ pour$ n≥1$

Réponse: $ a_n=0$si$ n$ est impair et$ a_n=2$ si$ n$ est pair

2)$ a_n=n^2−1$ pour$ n≥1$

3)$ a_1=1$ et$ a_n=a_{n−1}+n$ pour$ n≥2$

Réponse: $ {a_n}={1,3,6,10,15,21,…}$

4)$ a_1=1, a_2=1$ et$ a_n+2=a_n+a_{n+1}$ pour$ n≥1$

5) Trouvez une formule explicite pour savoir$ a_n$ où$ a_1=1$ et$ a_n=a_{n−1}+n$ pour$ n≥2$.

Réponse: $ a_n=\dfrac{n(n+1)}{2}$

6) Trouvez une formule$ a_n$ pour le$n^{\text{th}}$ terme de la séquence arithmétique dont le premier terme est$ a_1=1$ tel que$ a_{n−1}−a_n=17$ pour$ n≥1$.

7) Trouvez une formule$ a_n$ pour le$n^{\text{th}}$ terme de la séquence arithmétique dont le premier terme est$ a_1=−3$ tel que$ a_{n−1}−a_n=4$ pour$ n≥1$.

Réponse: $ a_n=4n−7$

8) Trouvez une formule$ a_n$ pour le$n^{\text{th}}$ terme de la séquence géométrique dont le premier terme est$ a_1=1$ tel que$ \dfrac{a_{n+1}}{a_n}=10$ pour$ n≥1$.

9) Trouvez une formule$ a_n$ pour le$n^{\text{th}}$ terme de la séquence géométrique dont le premier terme est$ a_1=3$ tel que$ \dfrac{a_{n+1}}{a_n}=1/10$ pour$ n≥1$.

Réponse: $ a_n=3.10^{1−n}=30.10^{−n}$

10) Trouvez une formule explicite pour le$n^{\text{th}}$ terme de la séquence dont les premiers termes sont$ {0,3,8,15,24,35,48,63,80,99,…}.$ (Conseil : ajoutez d'abord un terme à chaque terme.)

11) Trouvez une formule explicite pour le$n^{\text{th}}$ terme de la séquence satisfaisant$ a_1=0$ et$ a_n=2a_{n−1}+1$ pour$ n≥2$.

Réponse: $ a_n=2^n−1$

Dans les exercices 12 et 13, trouvez une formule pour le terme général$ a_n$ de chacune des séquences suivantes.

12)$ {1,0,−1,0,1,0,−1,0,…}$ (Conseil : trouvez où$\sin x$ prennent ces valeurs)

13)$ {1,−1/3,1/5,−1/7,…}$

Réponse: $ a_n=\dfrac{(−1)^{n−1}}{2n−1}$

Dans les exercices 14 à 18, trouvez une fonction$ f(n)$ qui identifie le$n^{\text{th}}$ terme$ a_n$ des séquences définies de manière récursive suivantes, comme$ a_n=f(n)$.

14)$ a_1=1$ et$ a_{n+1}=−a_n$ pour$ n≥1$

15)$ a_1=2$ et$ a_{n+1}=2a_n$ pour$ n≥1$

Réponse: $ f(n)=2^n$

16)$ a_1=1$ et$ a_{n+1}=(n+1)a_n$ pour$ n≥1$

17)$ a_1=2$ et$ a_{n+1}=(n+1)a_n/2$ pour$ n≥1$

Réponse: $f(n)=\dfrac{n!}{2^{n-2}}$

18)$ a_1=1$ et$ a_{n+1}=a_n/2^n$ pour$ n≥1$

Dans les exercices 19 à 22, tracez les premiers$ N$ termes de la séquence donnée. Indiquez si les preuves graphiques suggèrent que la séquence converge ou diverge.

19) [T]$ a_1=1, a_2=2$, et pour$ n≥2, a_n=\frac{1}{2}(a_{n−1}+a_{n−2})$ ;$ N=30$

Réponse

Les termes oscillent au-dessus et en dessous$ 5/3$ et semblent converger vers$ 5/3$.

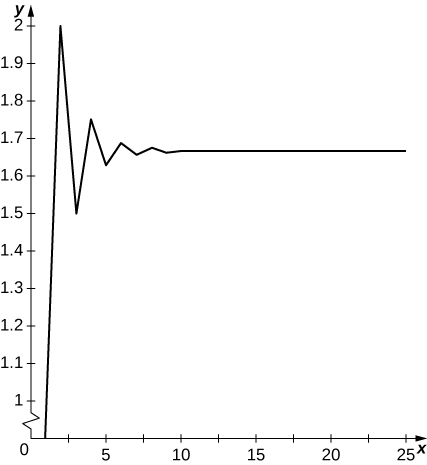
20) [T]$ a_1=1, a_2=2, a_3=3$ et pour$ n≥4, a_n=\frac{1}{3}(a_{n−1}+a_{n−2}+a_{n−3}), N=30$

21) [T]$ a_1=1, a_2=2$, et pour$ n≥3, a_n=\sqrt{a_{n−1}a_{n−2}}; N=30$

Réponse

Les termes oscillent au-dessus et en dessous$ y≈1.57..$ et semblent converger jusqu'à une limite.

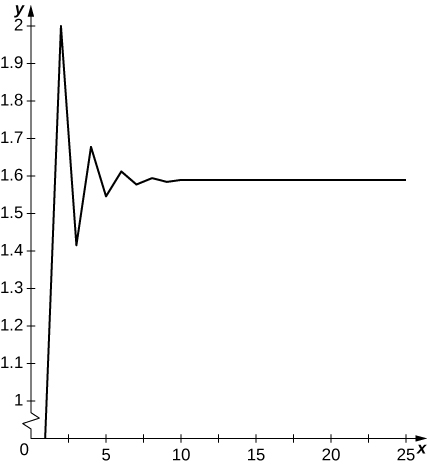
22) [T]$ a_1=1, a_2=2, a_3=3$, et pour$ n≥4, a_n=\sqrt{a_{n−1}a_{n−2}a_{n−3}}; N=30$

Dans les exercices 23 à 16, supposons cela$\displaystyle \lim_{n→∞}a_n=1, $$\displaystyle \lim_{n→∞}b_n=−1$, et$ 0<−b_n<a_n$ pour tous$ n$.

À l'aide de ces informations, évaluez chacune des limites suivantes, déterminez que la limite n'existe pas ou indiquez qu'il n'y a pas suffisamment d'informations pour déterminer si la limite existe.

23)$\displaystyle \lim_{n→∞}3a_n−4b_n$

Réponse: $\displaystyle \lim_{n→∞}3a_n−4b_n \quad = \quad 7$

(24)$\displaystyle \lim_{n→∞}\frac{1}{2}b_n−\frac{1}{2}a_n$

25)$\displaystyle \lim_{n→∞}\frac{a_n+b_n}{a_n−b_n}$

Réponse: $\displaystyle \lim_{n→∞}\frac{a_n+b_n}{a_n−b_n} \quad = \quad 0$

(26)$\displaystyle \lim_{n→∞}\frac{a_n−b_n}{a_n+b_n}$

Dans les exercices 27 à 30, déterminez la limite de chacune des séquences suivantes, en utilisant la règle de L'Hôpital le cas échéant.

(27)$ \dfrac{n^2}{2^n}$

Réponse: $\displaystyle \lim_{n→∞} \dfrac{n^2}{2^n} \quad = \quad 0$

(28)$ \dfrac{(n−1)^2}{(n+1)^2}$

(29)$ \dfrac{\sqrt{n}}{\sqrt{n+1}}$

Réponse: $\displaystyle \lim_{n→∞} \dfrac{\sqrt{n}}{\sqrt{n+1}} \quad = \quad 1 $

30)$ n^{1/n}$ (Astuce :$ n^{1/n}=e^{\frac{1}{n}\ln n})$

Dans les exercices 31 à 37, indiquez si chaque séquence est bornée et si elle est finalement monotone, croissante ou décroissante.

31)$ n/2^n, n≥2$

Réponse: borné, décroissant pour$ n≥1$

32)$ \ln\left(1+\dfrac{1}{n}\right)$

33)$ \sin n$

Réponse: borné, pas monotone

34)$ \cos(n^2)$

35)$ n^{1/n}, \quad n≥3$

Réponse: borné, décroissant

36)$ n^{−1/n}, \quad n≥3$

(37)$ \tan n$

Réponse: pas monotone, pas borné

Dans les exercices 38 à 39, déterminez si la séquence donnée a une limite. Si c'est le cas, trouvez la limite.

38)$ a_1=\sqrt{2}, a_2=\sqrt{2\sqrt{2}}. a_3=\sqrt{2\sqrt{2\sqrt{2}}}$ etc.

39)$ a_1=3, a_n=\sqrt{2a_{n−1}}, n=2,3,….$

Réponse: $ a_n$est décroissant et limité en dessous par$2$. La limite a doit$ a=\sqrt{2a}$ y satisfaire$ a=2$, indépendamment de la valeur initiale.

Utilisez le théorème de compression pour déterminer la limite de chaque séquence dans les exercices 40 à 43.

40)$ n\sin(1/n)$

41)$ \dfrac{\cos(1/n)−1}{1/n}$

Réponse: $0$

(42)$ a_n=\dfrac{n!}{n^n}$

43)$ a_n=\sin n \sin(1/n)$

Réponse: $ 0$depuis$|\sin x|≤|x|$ et ainsi de$ |\sin x|≤1$ suite$ −\dfrac{1}{n}≤a_n≤\dfrac{1}{n})$.

Pour les séquences des exercices 44 et 45, tracez les premiers$ 25$ termes de la séquence et indiquez si les preuves graphiques suggèrent que la séquence converge ou diverge.

44) [T]$ a_n=\sin n$

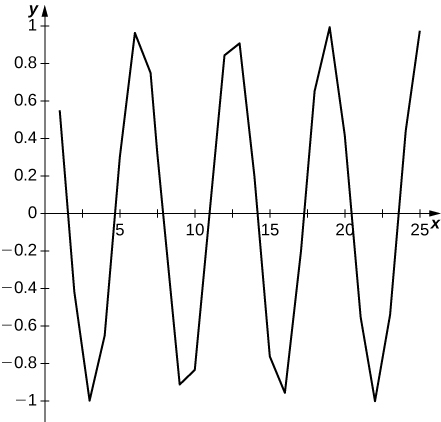
45) [T]$ a_n=\cos n$

Réponse

Le graphique oscille et ne suggère aucune limite.

Dans les exercices 46 à 52, déterminez la limite de la séquence ou montrez que la séquence diverge. S'il converge, trouvez sa limite.

46)$ a_n=\tan^{−1}(n^2)$

47)$ a_n=(2n)^{1/n}−n^{1/n}$

Réponse: $ n^{1/n}→1$et$ 2^{1/n}→1,$ donc$ a_n→0$

48)$ a_n=\dfrac{\ln(n^2)}{\ln(2n)}$

49)$ a_n=\left(1−\frac{2}{n}\right)^n$

Réponse: Depuis$ (1+1/n)^n→e$, on$ (1−2/n)^n≈(1+k)^{−2k}→e^{−2}$ a$ k→∞.$

50)$ a_n=\ln\left(\dfrac{n+2}{n^2−3}\right)$

51)$ a_n=\dfrac{2^n+3^n}{4^n}$

Réponse: $ 2^n+3^n≤2⋅3^n$et$ 3^n/4^n→0$$ n→∞$ en tant$ a_n→0$ que$ n→∞.$

52)$ a_n=\dfrac{(1000)^n}{n!}$

53)$ a_n=\dfrac{(n!)^2}{(2n)!}$

Réponse: $ \dfrac{a_{n+1}}{a_n}=n!/(n+1)(n+2)⋯(2n) =\dfrac{1⋅2⋅3⋯n}{(n+1)(n+2)⋯(2n)}<1/2^n$. En particulier$ a_{n+1}/a_n≤1/2$, de sorte$ a_n→0$ que$ n→∞$.

La méthode de Newton cherche à approximer une solution$ f(x)=0$ qui commence par une approximation initiale$ x_0$ et définit successivement une séquence$ x_{n+1}=x_n−\dfrac{f(x_n)}{f′(x_n)}$. Pour le choix donné de$ f$ et$ x_0$, écrivez la formule pour$ x_{n+1}$. Si la séquence semble converger, donnez une formule exacte pour la solution$ x$, puis identifiez la limite$ x$ précise à quatre décimales et la limite la plus$ n$ petite correspondant$ x_n$ à un$ x$ maximum de quatre décimales.

54) [T]$ f(x)=x^2−2,\quad x_0=1$

55) [T]$ f(x)=(x−1)^2−2,\quad x_0=2$

Réponse: \ (x_ {n+1} =x_n− ((x_n−1) ^2−2) /2 (
x_n−1) ; \ ; x=1+ \ sqrt {2}, \ ; x

56) [T]$ f(x)=e^x−2, \quad x_0=1$

57) [T]$ f(x)=\ln x−1,\quad x_0=2$

Réponse: \ (x_ {n+1} =x_n−x_n (\ ln (x_n) −1) ; \ ;
x=e, \ ; x=2 7183, \ ; n = 5 \)

58) [T] Supposons que vous commenciez avec un litre de vinaigre et que vous enleviez$0.1$ L à plusieurs reprises, que vous remplaciez par de l'eau, que vous mélange

a. Trouvez une formule pour la concentration après$ n$ les étapes.

b. Après combien d'étapes le mélange contient-il moins de$ 10\%$ vinaigre ?

59) [T] Un lac contient initialement du$ 2000$ poisson. Supposons qu'en l'absence de prédateurs ou d'autres causes d'élimination, la population de poissons augmente$ 6\%$ chaque mois. Cependant, si l'on tient compte de toutes les causes, des$ 150$ poissons sont perdus chaque mois.

a. Expliquez pourquoi la population de poissons après des$ n$ mois est modélisée à l'$ P_n=1.06P_{n−1}−150$aide de$ P_0=2000$.

b. Combien de poissons y aura-t-il dans l'étang après un an ?

Réponse: a. Sans pertes, la population obéirait$ P_n=1.06P_{n−1}$. La soustraction des$ 150$ comptes relatifs aux pertes de poissons.
b. Après des$ 12$ mois, nous avons$ P_{12}≈1494.$

60) [T] Un compte bancaire rapporte des$ 5\%$ intérêts composés mensuellement. Supposons qu'$ $1000$il soit initialement déposé sur le compte, mais qu'il$ $10$ soit retiré chaque mois.

a. Montrez que le montant sur le compte après des$ n$ mois est$ A_n=(1+.05/12)A_{n−1}−10; \; A_0=1000.$

b. Combien d'argent se trouvera-t-il sur le compte après un$ 1$ an ?

c. Le montant augmente-t-il ou diminue-t-il ?

d. Supposons qu'un montant fixe$ d$ en dollars soit retiré chaque mois.$ $10$ Trouvez une valeur$ d$ telle que le montant sur le compte après chaque mois reste$ $1000$.

e. Que se passe-t-il si le montant$ d$ est supérieur à ce montant ?

61) [T] Un étudiant contracte un prêt universitaire$ $10,000$ à un taux annuel en pourcentage$ 6\%,$ composé mensuellement.

a. Si l'étudiant effectue des paiements$ $100$ par mois, combien doit-il au bout de$ 12$ plusieurs mois ?

b. Après combien de mois le prêt sera-t-il remboursé ?

Réponse: a. L'étudiant doit au$ $9383$ bout de$ 12$ plusieurs mois.
b. Le prêt sera remboursé intégralement après des$ 139$ mois ou onze ans et demi.

62) [T] Considérons une série combinant croissance géométrique et décroissance arithmétique. Laissez$ a_1=1$. Corriger$ a>1$ et$ 0<b<a$. Définissez$ a_{n+1}=a.a_n−b.$ Trouvez une formule pour$ a_{n+1}$ en termes de$ a_n, a$, et$ b$ et une relation entre$ a$ et$ b$ telle que celle-ci$ a_n$ converge.

63) [T] La représentation binaire$ x=0.b_1b_2b_3...$ d'un nombre$ x$ compris entre$ 0$ et$ 1$ peut être définie comme suit. Laissez$ b_1=0$ si$ x<1/2$ et$ b_1=1$ si$ 1/2≤x<1.$ Laissez$ x_1=2x−b_1$. Laissez$ b_2=0$ si$ x_1<1/2$ et$ b_2=1$ si$ 1/2≤x<1$. Laissons$ x_2=2x_1−b_2$ et en général,$ x_n=2x_{n−1}−b_n$ et$ b_{n−}1=0$ si$ x_n<1/2$ et$ b_{n−1}=1$ si$ 1/2≤x_n<1$. Trouvez l'extension binaire de$ 1/3$.

Réponse: $ b_1=0, x_1=2/3, b_2=1, x_2=4/3−1=1/3,$donc le schéma se répète, et$ 1/3=0.010101….$

64) [T] Pour trouver une approximation pour$ π$$ a_0=\sqrt{2+1}, a_1=\sqrt{2+a_0}$, définir et, en général,$ a_{n+1}=\sqrt{2+a_n}$. Enfin, prêt$ p_n=3.2^n\sqrt{2−a_n}$. Trouvez les dix premiers termes de$ p_n$ et comparez les valeurs à$ π$.

Pour les deux exercices suivants, supposons que vous avez accès à un programme informatique ou à une source Internet capable de générer une liste de zéros et de uns de la longueur souhaitée. Les générateurs de nombres pseudo-aléatoires (PRNG) jouent un rôle important dans la simulation du bruit aléatoire dans les systèmes physiques en créant des séquences de zéros et de uns qui apparaissent comme le résultat de lancements répétés d'une pièce. L'un des types de PRNG les plus simples définit de manière récursive une séquence aléatoire d'$ N$entiers$ a_1,a_2,…,a_N$ en fixant deux entiers spéciaux$ (K$$ M$ et$ K.a_n$ en laissant$ a_{n+1}$ le reste après division$ M$, puis crée une séquence de bits de zéros et de uns dont $n^{\text{th}}$terme$ b_n$ est égal à un s'il$ a_n$ est impair et égal à zéro s'il$ a_n$ est pair. Si les bits$ b_n$ sont pseudo-aléatoires, le comportement de leur moyenne$ (b_1+b_2+⋯+b_N)/N$ doit être similaire au comportement des moyennes de bits générés de manière véritablement aléatoire.

65) [T] En commençant par$ K=16,807$ et$ M=2,147,483,647$ en utilisant dix valeurs de départ différentes de$ a_1$, calculez des séquences de bits$ b_n$ allant jusqu'à$ n=1000,$ et comparez leurs moyennes à dix séquences de ce type générées par un générateur de bits aléatoires.

Réponse: Pour les valeurs de départ,$ a_1=1, a_2=2,…, a_1=10,$ les moyennes de bits correspondantes calculées par la méthode indiquée sont$ 0.5220, 0.5000, 0.4960, 0.4870, 0.4860, 0.4680, 0.5130, 0.5210, 0.5040,$ et$ 0.4840$. Voici un exemple de dix moyennes correspondantes de chaînes de$ 1000$ bits générées par un générateur de nombres aléatoires :$ 0.4880, 0.4870, 0.5150, 0.5490, 0.5130, 0.5180, 0.4860, 0.5030, 0.5050, 0.4980.$ Il n'y a aucun schéma réel dans l'un ou l'autre type de moyenne. Les moyennes générées par des nombres aléatoires se situent entre$ 0.4860$ et$ 0.5490$, une plage de$ 0.0630$, tandis que les moyennes de bits PRNG calculées se situent entre$ 0.4680$ et$ 0.5220$, une plage de$ 0.0540.$

66) [T] Trouvez les premiers$ 1000$ chiffres de$ π$ l'utilisation d'un programme informatique ou d'une ressource Internet. Créez une séquence de bits$ b_n$ en indiquant$ b_n=1$ si le$n^{\text{th}}$ chiffre de$ π$ est impair et$ b_n=0$ si le$n^{\text{th}}$ chiffre de$ π$ est pair. Calculez la valeur moyenne de$ b_n$ et la valeur moyenne de La séquence$ d_n=|b_{n+1}−b_n|, n=1,...,999.$$ b_n$ apparaît-elle aléatoire ? Les différences entre les éléments successifs de$ b_n$ apparaissent-elles aléatoires ?