9.1 : Séquences
- Page ID
- 197762
- Trouvez la formule du terme général d'une séquence.
- Calculez la limite d'une séquence si elle existe.
- Déterminez la convergence ou la divergence d'une séquence donnée.
Dans cette section, nous présentons des séquences et définissons ce que cela signifie pour une séquence de converger ou de diverger. Nous montrons comment déterminer les limites des séquences qui convergent, souvent en utilisant les propriétés des limites des fonctions décrites précédemment. Nous clôturons cette section avec le théorème de convergence monotone, un outil que nous pouvons utiliser pour prouver que certains types de séquences convergent.
Terminologie des séquences
Pour travailler sur ce nouveau sujet, nous avons besoin de nouveaux termes et de nouvelles définitions. Tout d'abord, une séquence infinie est une liste ordonnée de nombres de la forme
\[a_1,a_2,a_3,…,a_n,….\nonumber \]
Chacun des nombres de la séquence est appelé terme. Le symbole\(n\) est appelé variable d'indice de la séquence. Nous utilisons la notation
\[\{a_n\}^∞_{n=1},\nonumber \]
ou simplement\(\{a_n\}\), pour désigner cette séquence. Une notation similaire est utilisée pour les ensembles, mais une séquence est une liste ordonnée, alors qu'un ensemble n'est pas ordonné. Comme\(a_n\) il existe un nombre particulier pour chaque entier positif\(n\), nous pouvons également définir une séquence comme une fonction dont le domaine est l'ensemble des entiers positifs.
Considérons la liste infinie et ordonnée
\[2,4,8,16,32,….\nonumber \]
Il s'agit d'une séquence dans laquelle les premier, deuxième et troisième termes sont donnés par\(a_1=2, a_2=4,\) et\(a_3=8.\) vous pouvez probablement constater que les termes de cette séquence ont le schéma suivant :
\[a_1=2^1,\,a_2=2^2,\,a_3=2^3,\,a_4=2^4 \text{ and } a_5=2^5.\nonumber \]
En supposant que ce schéma continue, nous pouvons écrire le\(n^{\text{th}}\) terme dans la séquence par la formule explicite.\(a_n=2^n.\) En utilisant cette notation, nous pouvons écrire cette séquence comme
\[\{2^n\}^∞_{n=1}\nonumber \]
ou
\[\{2^n\}.\nonumber \]
Nous pouvons également décrire cette séquence d'une manière différente. Comme chaque terme est le double du terme précédent, cette séquence peut être définie de manière récursive en exprimant le\(n^{\text{th}}\) terme\(a_n\) en termes du terme précédent\(a_{n−1}\). En particulier, on peut définir cette séquence comme la séquence\(\{a_n\}\) où,\(a_1=2\) et pour tous\(n≥2\), chaque terme an est défini par la relation de récurrence
\[a_n=2a_{n−1}. \nonumber \]
Une séquence infinie\(\{a_n\}\) est une liste ordonnée de nombres de la forme
\(a_1,\,a_2,\,…,\,a_n,\,….\)
L'indice\(n\) est appelé variable d'indice de la séquence. Chaque numéro\(a_n\) est un terme de la séquence. Parfois, les séquences sont définies par des formules explicites, auquel cas\(a_n=f(n)\) pour certaines fonctions, elles sont\(f(n)\) définies sur des entiers positifs. Dans d'autres cas, les séquences sont définies à l'aide d'une relation de récurrence. Dans une relation de récurrence, un terme (ou plus) de la séquence est indiqué explicitement, et les termes suivants sont définis en termes de termes antérieurs de la séquence.
Notez que l'index ne doit pas nécessairement commencer par d'autres entiers\(n=1\), mais qu'il peut commencer par d'autres entiers. Par exemple, une séquence donnée par la formule explicite\(a_n=f(n)\) pourrait commencer à\(n=0\), auquel cas la séquence serait
\[a_0,\,a_1,\,a_2,….\nonumber \]
De même, pour une séquence définie par une relation de récurrence, le terme\(a_0\) peut être donné explicitement, et les termes\(a_n\) pour\(n≥1\) peuvent être définis en termes de\(a_{n−1}\). Comme une séquence\(\{a_n\}\) possède exactement une valeur pour chaque entier positif\(n\), elle peut être décrite comme une fonction dont le domaine est l'ensemble des entiers positifs. Par conséquent, il est logique de discuter du graphe d'une séquence. Le graphe d'une séquence\(\{a_n\}\) comprend tous les points\((n,a_n)\) pour tous les entiers positifs n. La figure montre le graphique de\({2^n}\).
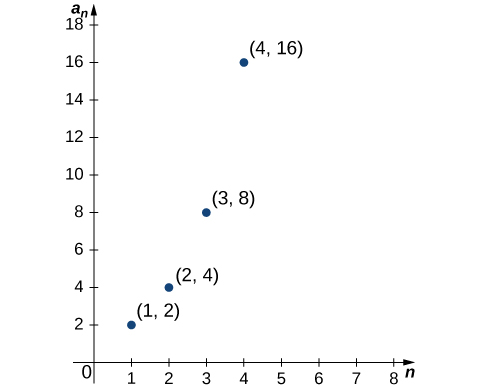
Deux types de séquences apparaissent souvent et portent des noms spéciaux : les séquences arithmétiques et les séquences géométriques. Dans une séquence arithmétique, la différence entre chaque paire de termes consécutifs est la même. Par exemple, considérez la séquence
\[3,\,7,\,11,\,15,1\,9, \,\ldots\nonumber \]
Vous pouvez voir que la différence entre chaque paire de termes consécutifs est\(4\). En supposant que ce schéma continue, il s'agit d'une séquence arithmétique. Il peut être décrit en utilisant la relation de récurrence
\[\begin{cases}a_1=3\\a_n=a_{n−1}+4, \text{ for }\ n≥2\end{cases}.\nonumber \]
Notez que
\[a_2=3+4\nonumber \]
\[a_3=3+4+4=3+2⋅4\nonumber \]
\[a_4=3+4+4+4=3+3⋅4.\nonumber \]
Ainsi, la séquence peut également être décrite à l'aide de la formule explicite
\[a_n=3+4(n−1)=4n−1.\nonumber \]
En général, une séquence arithmétique est une séquence quelconque de la forme\(a_n=cn+b.\)
Dans une séquence géométrique, le ratio de chaque paire de termes consécutifs est le même. Par exemple, considérez la séquence
\[2,\,−\dfrac{2}{3},\,\dfrac{2}{9},\,−\dfrac{2}{27},\,\dfrac{2}{81},….\nonumber \]
Nous voyons que le rapport entre un terme et le terme précédent est de\(−\dfrac{1}{3}\). En supposant que ce schéma persiste, cette séquence est une séquence géométrique. Il peut être défini de manière récursive comme
\[ a_1=2\nonumber \]
\[a_n=−\dfrac{1}{3}⋅a_{n−1}, \text{ for }\ n≥2.\nonumber \]
Alternativement, puisque
\[ \begin{align*} a_2 &=−\dfrac{1}{3}⋅2 \\[4pt] a_3 &=\left(−\dfrac{1}{3}\right)\left(−\dfrac{1}{3}\right)(2)=\left(−\dfrac{1}{3}\right)^2⋅2 \\[4pt] a_4 &= \left(−\dfrac{1}{3}\right)\left(−\dfrac{1}{3}\right)\left(−\dfrac{1}{3}\right)(2)=\left(−\dfrac{1}{3}\right)^3⋅2,\end{align*} \nonumber \]
nous voyons que la séquence peut être décrite en utilisant la formule explicite
\[a_n=2 \left(−\dfrac{1}{3}\right)^{n−1}.\nonumber \]
La séquence\(\{2^n\}\) dont nous avons parlé plus tôt est une séquence géométrique, où le rapport entre un terme et le terme précédent est\(2\). En général, une séquence géométrique est une séquence quelconque du formulaire\(a_n=cr^n\).
Pour chacune des séquences suivantes, trouvez une formule explicite pour le\(n^{\text{th}}\) terme de la séquence.
- \(−\dfrac{1}{2},\dfrac{2}{3},−\dfrac{3}{4},\dfrac{4}{5},−\dfrac{5}{6},…\)
- \(\dfrac{3}{4},\dfrac{9}{7},\dfrac{27}{10},\dfrac{81}{13},\dfrac{243}{16},…\).
Solution
a. Tout d'abord, notez que la séquence alterne du négatif au positif. Les termes impairs de la séquence sont négatifs et les termes pairs sont positifs. Par conséquent, le\(n^{\text{th}}\) terme inclut un facteur de\((−1)^n\). Ensuite, considérez la séquence des numérateurs\({1,2,3,…}\) et la séquence des dénominateurs\({2,3,4,…}\). Nous pouvons voir que ces deux séquences sont des séquences arithmétiques. Le\(n^{\text{th}}\) terme dans la séquence de numérateurs est\(n\), et le\(n^{\text{th}}\) terme dans la séquence de dénominateurs est\(n+1\). Par conséquent, la séquence peut être décrite par la formule explicite
\[a_n=\dfrac{(−1)^nn}{n+1}. \nonumber \]
b. La séquence de numérateurs\(3,9,27,81,243,…\) est une séquence géométrique. Le numérateur du\(n^{\text{th}}\) terme est\(3^n\) La séquence des dénominateurs\(4,7,10,13,16,…\) est une séquence arithmétique. Le dénominateur du\(n^{\text{th}}\) terme est\(4+3(n−1)=3n+1.\) Par conséquent, nous pouvons décrire la séquence par la formule explicite\(a_n=\dfrac{3^n}{3n+1.}\)
Trouvez une formule explicite pour le\(n^{\text{th}}\) terme de la séquence\(\left\{\dfrac{1}{5},−\dfrac{1}{7},\dfrac{1}{9},−\dfrac{1}{11},…\right\}.\)
- Allusion
-
Les dénominateurs forment une suite arithmétique.
- Réponse
-
\(a_n=\dfrac{(−1)^{n+1}}{3+2n}\)
Pour chacune des séquences définies de manière récursive suivantes, trouvez une formule explicite pour la séquence.
- \(a_1=2, a_n=−3a_{n−1}\)pour\(n≥2\)
- \(a_1=\left(\dfrac{1}{2}\right), a_n=a_{n−1}+\left(\dfrac{1}{2}\right)^n\)pour\(n≥2\)
Solution
a. Pour rédiger les premiers termes, nous avons
\[ \begin{align*} a_1 &=2 \\[4pt] a_2 &=−3a_1=−3(2)\\[4pt] a_3 &=−3a_2=(−3)^22\\[4pt] a_4 &=−3a_3=(−3)^32.\end{align*}\]
D'une manière générale,
\(a_n=2(−3)^{n−1}.\)
b. Écrivez les premiers termes :
\(a_1=\dfrac{1}{2}\)
\(a_2=a_1+\left(\dfrac{1}{2}\right)^2=\dfrac{1}{2}+\dfrac{1}{4}=\dfrac{3}{4}\)
\(a_3=a_2+\left(\dfrac{1}{2}\right)^3=\dfrac{3}{4}+\dfrac{1}{8}=\dfrac{7}{8}\)
\(a_4=a_3+\left(\dfrac{1}{2}\right)^4=\dfrac{7}{8}+\dfrac{1}{16}=\dfrac{15}{16}\).
De ce modèle, nous dérivons la formule explicite
\(a_n=\dfrac{2^n−1}{2^n}=1−\dfrac{1}{2^n}\).
Trouvez une formule explicite pour la séquence définie de manière récursive telle que\(a_1=−4\) et\(a_n=a_{n−1}+6\).
- Allusion
-
Il s'agit d'une séquence arithmétique.
- Réponse
-
\(a_n=6n−10\)
Limite d'une séquence
Une question fondamentale qui se pose concernant les séquences infinies est le comportement des termes au fur et à mesure qu'ils\(n\) s'agrandissent. Puisqu'une séquence est une fonction définie sur les entiers positifs, il est logique de discuter de la limite des termes comme\(n→∞\). Par exemple, considérez les quatre séquences suivantes et leurs différents comportements comme suit\(n→∞\) (Figure\(\PageIndex{2}\)) :
- \(\{1+3n\}=\{4,7,10,13,…\}.\)Les termes\(1+3n\) deviennent arbitrairement longs à mesure que\(n→∞\). Dans ce cas, nous disons\(1+3n→∞\) que\(n→∞.\)
- \(\left\{1− \left(\dfrac{1}{2}\right) ^n\right\}=\left\{ \dfrac{1}{2} ,\dfrac{3}{4},\dfrac{7}{8},\dfrac{15}{16}\,…\right\}.\)Les termes en\(1−\left(\dfrac{1}{2}\right)^n→1\) tant que\(n→∞.\)
- \(\{(−1)^n\}=\{−1,1,−1,1,…\}.\)Les termes alternent mais ne se rapprochent pas d'une seule valeur comme\(n→∞.\)
- \(\left\{\dfrac{(−1)^n}{n}\right\}=\left\{−1,\dfrac{1}{2},−\dfrac{1}{3},\dfrac{1}{4},…\right\}.\)Les termes alternent également pour cette séquence, mais\(\dfrac{(−1)^n}{n}→0\) comme\(n→∞.\)
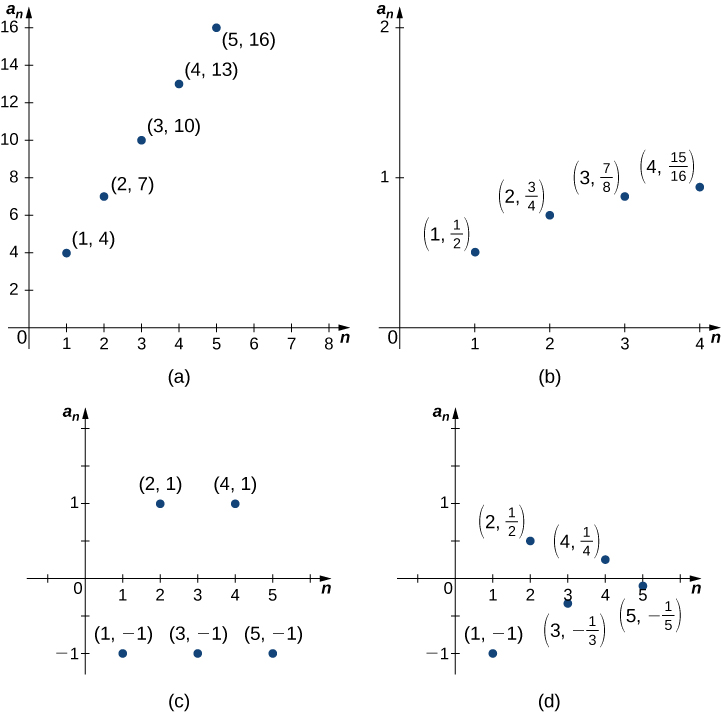
À partir de ces exemples, nous voyons plusieurs possibilités pour le comportement des termes d'une séquence en tant que\(n→∞\). Dans deux des séquences, les termes se rapprochent d'un nombre fini, alors que\(n→∞.\) dans les deux autres séquences, les termes ne le sont pas. Si les termes d'une séquence s'approchent d'un nombre fini\(L\) comme\(n→∞\), nous disons que la séquence est une séquence convergente et que le nombre réel L est la limite de la séquence. Nous pouvons donner une définition informelle ici.
Étant donné une séquence,\({a_n},\) si les termes peuvent devenir arbitrairement proches d'un nombre\(L\) fini lorsque n devient suffisamment grand, nous disons qu'\(\{a_n\}\)il s'agit d'une séquence convergente et\(L\) constitue la limite de la séquence. Dans ce cas, nous écrivons
\[\lim_{n→∞}a_n=L. \nonumber \]
Si une séquence n'\(\{a_n\}\)est pas convergente, on dit qu'il s'agit d'une séquence divergente.
À partir de la figure, nous voyons que les termes de la séquence se\(\left\{1− \left(\dfrac{1}{2}\right)^n\right\}\) rapprochent arbitrairement à\(1\) mesure qu'ils\(n\) deviennent très grands. Nous concluons qu'il\(\left\{1−\left(\dfrac{1}{2}\right)^n\right\}\) s'agit d'une séquence convergente et que sa limite est\(1\). En revanche, à partir de la Figure, nous voyons que les termes de la séquence ne se\(1+3n\) rapprochent pas d'un nombre fini à mesure\(n\) qu'ils augmentent. Nous disons qu'il\(\{1+3n\}\) s'agit d'une séquence divergente.
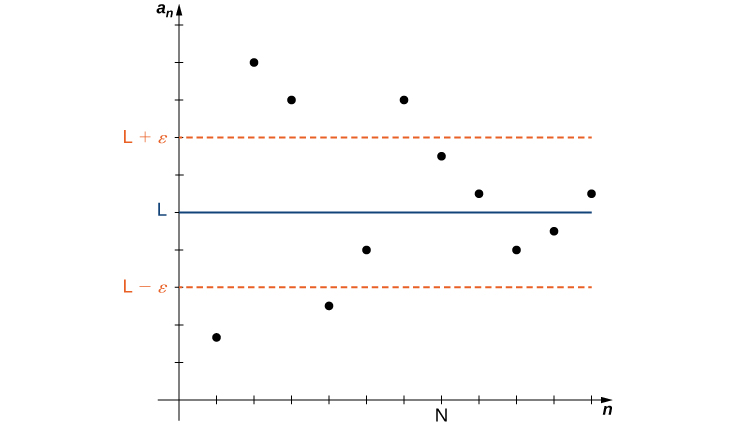
Dans la définition informelle de la limite d'une séquence, nous avons utilisé les termes « arbitrairement proche » et « suffisamment grande ». Bien que ces phrases aident à illustrer la signification d'une séquence convergente, elles sont quelque peu vagues. Pour être plus précis, nous présentons maintenant la définition plus formelle de la limite pour une séquence et montrons ces idées graphiquement dans la figure.
Une séquence\(\{a_n\}\) converge vers un nombre réel\(L\) si pour tous\(ε>0\), il existe un entier\(N\) tel que pour tous\(n ≥ N\)\(|a_n−L| < ε\). Le nombre\(L\) est la limite de la séquence et on écrit
\[\lim_{n→∞}a_n = L \text{ or } a_n→L. \nonumber \]
Dans ce cas, on dit que la séquence\(\{a_n\}\) est une séquence convergente. Si une séquence ne converge pas, c'est une séquence divergente, et nous disons que la limite n'existe pas.
Nous remarquons que la convergence ou la divergence d'une séquence\(\{a_n\}\) dépend uniquement de ce qu'il advient des termes en\(a_n\) tant que\(n→∞\). Par conséquent, si un nombre limité de termes\(b_1,b_2,…,b_N\) sont placés avant\(a_1\) pour créer une nouvelle séquence
\[b_1,\,b_2,\,…,\,b_N,\,a_1,\,a_2,\,…,\nonumber \]
cette nouvelle séquence convergera si elle\(\{a_n\}\) converge et divergera si elle\(\{a_n\}\) diverge. De plus, si la séquence\(\{a_n\}\) converge vers\(L\), cette nouvelle séquence convergera également vers\(L\).
Comme défini ci-dessus, si une séquence ne converge pas, on dit qu'il s'agit d'une séquence divergente. Par exemple, les séquences\(\{1+3n\}\) et celles\(\left\{(−1)^n\right\}\) présentées dans la figure divergent. Cependant, différentes séquences peuvent diverger de différentes manières. La séquence\(\left\{(−1)^n\right\}\) diverge parce que les termes alternent entre\(1\) et\(−1\), mais ne se rapprochent pas d'une valeur comme\(n→∞\). D'un autre côté, la séquence\(\{1+3n\}\) diverge car les termes\(1+3n→∞\) as\(n→∞\). On dit que la séquence\(\{1+3n\}\) diverge à l'infini et qu'elle écrit\(\displaystyle \lim_{n→∞}(1+3n)=∞\). Il est important de reconnaître que cette notation n'implique pas que la limite de la séquence\(\{1+3n\}\) existe. La séquence est en fait divergente. Écrire que la limite est infinie vise uniquement à fournir plus d'informations sur les raisons pour lesquelles la séquence est divergente. Une séquence peut également diverger vers l'infini négatif. Par exemple, la séquence\(\{−5n+2\}\) diverge vers l'infini négatif\(−5n+2→−∞\) car\(n→−∞\). Nous écrivons ceci comme\(\displaystyle \lim_{n→∞}(−5n+2)=→−∞.\)
Comme une séquence est une fonction dont le domaine est l'ensemble des entiers positifs, nous pouvons utiliser les propriétés des limites des fonctions pour déterminer si une séquence converge. Par exemple, considérez une séquence\(\{a_n\}\) et une fonction associée\(f\) définies sur tous les nombres réels positifs, de telle sorte que\(f(n)=a_n\) pour tous les entiers\(n≥1\). Puisque le domaine de la séquence est un sous-ensemble du domaine de\(f\), s'\(\displaystyle \lim_{x→∞}f(x)\)il existe, alors la séquence converge et a la même limite. Par exemple, considérez la séquence\(\left\{\dfrac{1}{n}\right\}\) et la fonction associée\(f(x)=\dfrac{1}{x}\). Puisque la fonction\(f\) définie sur tous les nombres réels\(x>0\) satisfait\(f(x)=\dfrac{1}{x}→0\) à\(x→∞\), la séquence\(\left\{\dfrac{1}{n}\right\}\) doit satisfaire\(\dfrac{1}{n}→0\) à\(n→∞.\)
Envisagez une séquence\(\{a_n\}\) qui s'\(a_n=f(n)\)applique à tous\(n≥1\). S'il existe un nombre réel\(L\) tel que
\[\lim_{x→∞}f(x)=L, \nonumber \]
puis\(\{a_n\}\) converge et
\[\lim_{n→∞}a_n=L. \nonumber \]
Nous pouvons utiliser ce théorème\(\displaystyle \lim_{n→∞}r^n\) pour évaluer\(0≤r≤1\). Par exemple, considérez la séquence\(\left\{(1/2)^n\right\}\) et la fonction exponentielle associée\(f(x)=(1/2)^x\). Depuis\(\displaystyle \lim_{x→∞}(1/2)^x=0\), nous concluons que la séquence\(\left\{(1/2)^n\right\}\) converge et que sa limite est\(0\). De même, pour tout nombre réel\(r\) tel que\(0≤r<1\)\(\displaystyle \lim_{x→∞}r^x=0\), et donc la séquence\(\left\{r^n\right\}\) converge. D'un autre côté, si\(r=1\), alors\(\displaystyle \lim_{x→∞}r^x=1\), et donc la limite de la séquence\(\left\{1^n\right\}\) est\(1\). Si\(r>1\), et donc\(\displaystyle \lim_{x→∞}r^x=∞\), nous ne pouvons pas appliquer ce théorème. Cependant, dans ce cas, tout comme la fonction\(r^x\) croît sans limite au fur et à mesure que\(n→∞\), les\(r^n\) termes de la séquence deviennent arbitrairement grands comme\(n→∞\), et nous concluons que la séquence\(\left\{r^n\right\}\) diverge à l'infini si\(r>1\).
Nous résumons ces résultats concernant la séquence géométrique\({r^n}\) :
\(r^n→0\)si\(0<r<1\)
\(r^n→1\)si\(r=1\)
\(r^n→∞\)si\(r>1\).
Plus loin dans cette section, nous examinerons le cas où\(r<0\).
Nous considérons maintenant des séquences un peu plus compliquées. Par exemple, considérez la séquence\(\left\{(2/3)^n+(1/4)^n\right\}.\) Les termes de cette séquence sont plus compliqués que les autres séquences dont nous avons parlé, mais heureusement, la limite de cette séquence est déterminée par les limites des deux séquences\(\left\{(2/3)^n\right\}\) et\(\left\{(1/4)^n\right\}\). Comme nous le décrivons dans les lois limites algébriques suivantes, puisque\(\left\{(2/3)^n\right\}\) et\(\left\{1/4)^n\right\}\) les deux convergent vers\(0\), la séquence\(\left\{(2/3)^n+(1/4)^n\right\}\) converge vers\(0+0=0\). Tout comme nous avons pu évaluer une limite impliquant une combinaison algébrique de fonctions\(f\) et\(g\) en examinant les limites de\(f\) et\(g\) (voir Introduction aux limites), nous sommes en mesure d'évaluer la limite d'une séquence dont les termes sont des combinaisons algébriques de\(a_n\) et \(b_n\)en évaluant les limites de\(\{a_n\}\) et\(\{b_n\}\).
Des séquences données\(\{a_n\}\)\(\{b_n\}\) et n'importe quel nombre réel\(c\), s'il existe des constantes\(A\) et\(B\) telles que\(\displaystyle \lim_{n→∞}a_n=A\) et\(\displaystyle \lim_{n→∞}b_n=B\),
- \(\displaystyle \lim_{n→∞}c=c\)
- \(\displaystyle \lim_{n→∞}ca_n=c\lim_{n→∞}a_n=cA\)
- \(\displaystyle \lim_{n→∞}(a_n±b_n)=\lim_{n→∞}a_n±\lim_{n→∞}b_n=A±B\)
- \(\displaystyle \lim_{n→∞}(a_n⋅b_n)=\big(\lim_{n→∞}a_n\big)⋅\big(\lim_{n→∞}b_n\big)=A⋅B\)
- \(\displaystyle \lim_{n→∞}\left(\dfrac{a_n}{b_n}\right)=\dfrac{\lim_{n→∞}a_n}{\lim_{n→∞}b_n}=\dfrac{A}{B}\), fournis\(B≠0\) et chacun\(b_n≠0.\)
Nous prouvons la partie III.
Laissez\(ϵ>0\). Depuis\(\displaystyle \lim_{n→∞}a_n=A\), il existe un entier positif constant\(N_1\) tel que pour tous\(n≥N_1\). Depuis\(\displaystyle \lim_{n→∞}b_n=B\), il existe une constante\(N_2\) telle que\(|b_n−B|<ε/2\) pour tous\(n≥N_2\). \(N\)Soyons le plus grand des\(N_1\) et\(N_2\). Donc, pour tous\(n≥N\),\(|(a_n+b_n)−(A+B)|≤|a_n−A|+|b_n−B|<\dfrac{ε}{2}+\dfrac{ε}{2}=ε\).
□
Les lois des limites algébriques nous permettent d'évaluer les limites de nombreuses séquences. Par exemple, considérez la séquence\(a_n={\dfrac{1}{n^2}}\). Comme indiqué précédemment,\(\displaystyle \lim_{n→∞}\dfrac{1}{n}=0\). De même, pour tout entier positif\(k\), nous pouvons conclure que
\[\lim_{n→∞}\dfrac{1}{n^k}=0. \nonumber \]
Dans l'exemple suivant, nous utilisons ce fait ainsi que les lois limites pour évaluer les limites d'autres séquences.
Pour chacune des séquences suivantes, déterminez si la séquence converge ou non. S'il converge, trouvez sa limite.
- \(\left\{5−\dfrac{3}{n^2}\right\}\)
- \(\left\{\dfrac{3n^4−7n^2+5}{6−4n^4}\right\}\)
- \(\left\{\dfrac{2^n}{n^2}\right\}\)
- \(\left\{\left(1+\dfrac{4}{n}\right)^n\right\}\)
Solution
a. Nous le savons\(\displaystyle \lim_{n→∞}\dfrac{1}{n}=0\). Sur la base de ce fait, nous concluons que
\(\displaystyle \lim_{n→∞}\dfrac{1}{n^2}=\lim_{n→∞}\dfrac{1}{n}.\lim_{n→∞}\dfrac{1}{n}=0.\)
Par conséquent,
\(\displaystyle \lim_{n→∞}\left(5−\dfrac{3}{n^2}\right)=\lim_{n→∞}5−3\lim_{n→∞}\dfrac{1}{n^2}=5−3.0=5.\)
La séquence converge et sa limite est de 5.
b. En tenant compte\(n^4\) du numérateur et du dénominateur et en utilisant les lois limites ci-dessus, nous avons
\ [\ begin {align*} \ lim_ {n→∞} \ dfrac {3n^4−7n^2+5} {6−4n^4} &= \ lim_ {n→∞} \ dfrac {3− \ dfrac {7} {n^2} + \ dfrac {5} {n^4}} {\ dfrac {6} {n^2} + \ dfrac {5} {n^4}} {\ dfrac {6} {n^4}} −4} \ \ [5 points]
&= \ dfrac {\ lim_ {n→∞} (3− \ dfrac {7} {n^2} + \ dfrac {5} {n^4})} {\ lim_ {n→∞} (\ dfrac {6} {n^4} −4)} \ \ [5 points]
&= \ dfrac {\ lim_ {n→∞} (3) − \ lim_ {n→∞} \ dfrac {7} {n^2} + \ lim_ {n→∞} \ dfrac {5} {n^4}} {\ lim_ {n→∞} \ dfrac {6} {n^4} − \ lim_ {n→∞} (4)} \ \ [5 points]
&= \ dfrac {\ lim_ {n→∞} (3) −7⋅ \ lim_ {n→∞} \ dfrac {1} {n^2} +5⋅ \ lim_ {n→∞} \ dfrac {1} {n^4}} {6⋅ \ lim_ {n→∞} \ dfrac {1} {n^4} − \ lim_ {n→∞} (4)} \ \ [5 points]
&= \ dfrac {3−7⋅0+5⋅0} {6⋅0−0−4}} =− \ frac {3} {4}. \ end {align*} \]
La séquence converge et sa limite est\(−3/4\).
c. Considérez la fonction associée\(f(x)=2^x/x^2\) définie sur tous les nombres réels\(x>0\). Depuis\(2^x→∞\) et au\(x^2→∞\) fur et à mesure\(x→∞\), appliquez la règle de L'Hôpital et écrivez
\ [\ begin {align*} \ lim_ {x→∞} \ dfrac {2^x} {x^2} &= \ lim_ {x→∞} \ dfrac {2^x \ ln2} {2x} & & \ text {Prenez les dérivées du numérateur et du dénominateur.} \ \ [5pt]
&= \ lim_ {x→∞} \ dfrac {2} ^x (\ ln2) ^2} {2} & & \ text {Reprenez les dérivées.} \ \ [5 points]
&=∞. \ end {align*} \]
Nous concluons que la séquence diverge.
d. Considérez la fonction\(f(x)=\left(1+\dfrac{4}{x}\right)^x\) définie sur tous les nombres réels\(x>0\). Cette fonction a la forme indéterminée\(1^∞\)\(x→∞.\) Let.
\(\displaystyle y=\lim_{x→∞}\left(1+\dfrac{4}{x}\right)^x\).
Maintenant, en prenant le logarithme naturel des deux côtés de l'équation, nous obtenons
\(\displaystyle \ln(y)=\ln\left[\lim_{x→∞}\left(1+\dfrac{4}{x}\right)^x\right]\).
Comme la fonction\(f(x)=\ln(x)\) est continue dans son domaine, nous pouvons échanger la limite et le logarithme naturel. Par conséquent,
\(\displaystyle \ln(y)=\lim_{x→∞}\left[\ln\left(1+\dfrac{4}{x}\right)^x\right]\).
En utilisant les propriétés des logarithmes, nous écrivons
\(\displaystyle \lim_{x→∞}\left[\ln\left(1+\dfrac{4}{x}\right)^x\right]=\lim_{x→∞}x\ln\left(1+\dfrac{4}{x}\right)\).
Comme la partie droite de cette équation a la forme indéterminée\(∞⋅0\), réécrivez-la sous forme de fraction pour appliquer la règle de L'Hôpital. Écrivez
\(\displaystyle \lim_{x→∞}x\ln\left(1+\dfrac{4}{x}\right)=\lim_{x→∞}\dfrac{\ln\left(1+4/x\right)}{1/x}\).
Comme le côté droit est désormais dans la forme indéterminée 0/0, nous sommes en mesure d'appliquer la règle de L'Hôpital. Nous concluons que
\(\displaystyle \lim_{x→∞}\dfrac{\ln(1+4/x)}{1/x}=\lim_{x→∞}\dfrac{4}{1+4/x}=4.\)
Donc,\(\ln(y)=4\) et\(y=e^4\). Par conséquent, puisque\(\displaystyle \lim_{x→∞}\left(1+\dfrac{4}{x}\right)^x=e^4\), nous pouvons conclure que la séquence\(\left\{\left(1+\dfrac{4}{n}\right)^n\right\}\) converge vers\(e^4\).
Examinez la séquence\(\left\{(5n^2+1)/e^n\right\}.\) Déterminez si la séquence converge ou non. S'il converge, trouvez sa limite.
- Allusion
-
Utilisez la règle de L'Hôpital.
- Réponse
-
La séquence converge et sa limite est\(0\)
Rappelez-vous que s'il s'\(f\)agit d'une fonction continue à une valeur\(L\), alors\(f(x)→f(L)\) en tant que\(x→L\). Cette idée s'applique également aux séquences. Supposons qu'\(a_n→L\)il s'agisse d'une séquence et qu'une fonction\(f\) soit continue à\(L\). Alors\(f(a_n)→f(L)\). Cette propriété nous permet souvent de trouver des limites pour des séquences complexes. Par exemple, considérez la séquence\(\sqrt{5−\dfrac{3}{n^2}}\). À partir de l'exemple a. nous connaissons la séquence\(5−\dfrac{3}{n^2}→5\). Comme\(\sqrt{x}\) il s'agit d'une fonction continue chez\(x=5\),
\[\lim_{n→∞}\sqrt{5−\dfrac{3}{n^2}}=\sqrt{\lim_{n→∞}(5−\dfrac{3}{n^2})}=\sqrt{5}.\nonumber \]
Considérez une séquence\(\{a_n\}\) et supposons qu'il existe un nombre réel\(L\) tel que la séquence\(\{a_n\}\) converge vers\(L\). Supposons qu'\(f\)il y ait une fonction continue à\(L\). Il existe alors un entier\(N\) défini pour toutes les valeurs et tous les pour\(n≥N\), et la séquence\(\{f(a_n)\}\) converge vers\(f(L)\) (Figure\(\PageIndex{4}\)).\(f\)
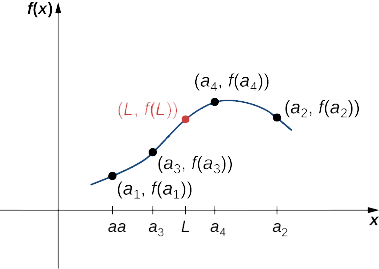
Let\(ϵ>0.\)\(f\) Since est continu à\(L\), il existe\(δ>0\) tel que\(|f(x)−f(L)|<ε\) si\(|x−L|<δ\). Puisque la séquence\(\{a_n\}\) converge vers\(L\), il existe\(N\) une telle chose\(|a_n−L|<δ\) pour tous\(n≥N\). Donc, pour tous\(n≥N\)\(|a_n−L|<δ\), ce qui implique\(|f(a_n)−f(L)|<ε\). Nous concluons que la séquence\(\{f(a_n)\}\) converge vers\(f(L)\).
□
Déterminez si la séquence\(\left\{\cos(3/n^2)\right\}\) converge. S'il converge, trouvez sa limite.
Solution :
Puisque la séquence\(\left\{3/n^2\right\}\) converge vers\(0\) et\(\cos x\) est continue à\(x=0\), nous pouvons en conclure que la séquence\(\left\{\cos(3/n^2)\right\}\) converge et
\(\displaystyle \lim_{n→∞}\cos\left(\dfrac{3}{n^2}\right)=\cos 0=1.\)
Déterminez si la séquence\(\left\{\sqrt{\dfrac{2n+1}{3n+5}}\right\}\) converge. S'il converge, trouvez sa limite.
- Allusion
-
Considérez la séquence\(\left\{\dfrac{2n+1}{3n+5}\right\}.\)
- Réponse
-
La séquence converge et sa limite est\(\sqrt{2/3}\).
Un autre théorème impliquant les limites des séquences est une extension du théorème de compression pour les limites discuté dans Introduction aux limites.
Considérez les séquences\(\{a_n\}, \, \{b_n\},\) et\(\{c_n\}\). Supposons qu'il existe un entier\(N\) tel que
\(a_n≤b_n≤c_n\)pour tous\(n≥N.\)
S'il existe un nombre réel\(L\) tel que
\[\lim_{n→∞}a_n=L=\lim_{n→∞}c_n, \nonumber \]
\(\{b_n\}\)converge alors et\(\displaystyle \lim_{n→∞}b_n=L\) (Figure\(\PageIndex{5}\)).
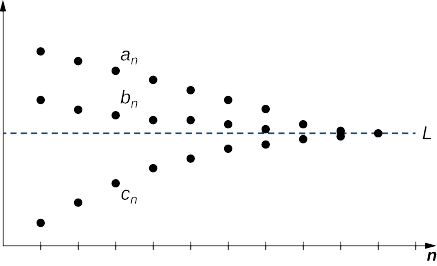
Soit\(ε>0.\) Puisque la séquence\(\{a_n\}\) converge vers\(L\), il existe un entier\(N_1\) tel que\(|a_n−L|<ε\) pour tous\(n≥N_1\). De même, puisque\(\{c_n\}\) converge vers\(L\), il existe un entier\(N_2\) tel que\(|c_n−L|<ε\) pour tous\(n≥N_2\). Par hypothèse, il existe un entier\(N\) tel que\(a_n≤b_n≤c_n\) pour tous\(n≥N\). \(M\)Soyons le plus grand des\(N_1,\, N_2\), et\(N\). Nous devons le montrer\(|b_n−L|<ε\) à tous\(n≥M\). Pour tous\(n≥M\),
\[−ε<−|a_n−L|≤a_n−L≤b_n−L≤c_n−L≤|c_n−L|<ε\nonumber \]
Par conséquent,\(−ε<b_n−L<ε,\) nous concluons cela\(|b_n−L|<ε\) pour tous\(n≥M\), et nous concluons que la séquence\({b_n}\) converge vers\(L\).
□
Utilisez le théorème de compression pour déterminer la limite de chacune des séquences suivantes.
- \(\left\{\dfrac{\cos\, n}{n^2}\right\}\)
- \(\left\{\left(−\dfrac{1}{2}\right)^n\right\}\)
Solution
a. Puisque\(−1≤\cos n≤1\) pour tous les entiers\(n\), nous avons
\(−\dfrac{1}{n^2} ≤ \dfrac{\cos n}{n^2}≤\dfrac{1}{n^2}.\)
Depuis\(−1/n^2→0\) et\(1/n^2→0\), nous concluons\(\cos n/n^2→0\) que c'est également le cas.
b. Depuis
\(−\dfrac{1}{2^n} ≤ \left(−\dfrac{1}{2}\right)^n ≤ \dfrac{1}{2^n}\)
pour tous les entiers positifs\(n, \, −1/2^n→0\) et\(1/2^n→0,\) nous pouvons en conclure que\((−1/2)^n→0.\)
Trouvez\(\displaystyle \lim_{n→∞}\dfrac{2n−\sin\, n}{n}.\)
- Allusion
-
Utilisez le fait que\(−1≤\sin n≤1.\)
- Réponse
-
\(2\)
En utilisant l'idée de Example,\(\PageIndex{5}\) b nous concluons que\(r^n→0\) pour tout nombre réel r tel que\(−1<r<0.\) If\(r<−1\), la séquence\({r^n}\) diverge parce que les termes oscillent et deviennent arbitrairement importants en amplitude. Si\(r=−1\), la séquence\({r^n}={(−1)^n}\) diverge, comme indiqué précédemment. Voici un résumé des propriétés des séquences géométriques.
\(r^n→0 \text{ if } |r|<1\)
\(r^n→1\text{ if } r=1\)
\(r^n→∞\text{ if } r>1\)
\(\left\{r^n\right\} \text{ diverges if } r≤−1\)
Séquences bornées
Nous allons maintenant porter notre attention sur l'un des plus importants théorèmes impliquant des séquences : le théorème de convergence monotone. Avant d'énoncer le théorème, nous devons introduire une terminologie et une motivation. Nous commençons par définir ce que signifie le fait qu'une séquence soit délimitée.
Une séquence\(\{a_n\}\) est bornée au-dessus s'il existe un nombre réel\(M\) tel que
\(a_n≤M\)
pour tous les entiers positifs\(n\).
Une séquence\(\{a_n\}\) est bornée en dessous s'il existe un nombre réel\(m\) tel que
\(m≤a_n\)
pour tous les entiers positifs\(n\).
Une séquence\(\{a_n\}\) est une séquence bornée si elle est bornée au-dessus et inférieure.
Si une séquence n'est pas bornée, il s'agit d'une séquence illimitée.
Par exemple, la séquence\(\{1/n\}\) est bornée au-dessus car\(1/n≤1\) pour tous les entiers positifs\(n\). Il est également limité en dessous car\(1/n≥0\) pour tous les entiers positifs\(n\). Par conséquent,\(\{1/n\}\) est une séquence bornée. D'un autre côté, considérez la séquence\(\left\{2^n\right\}\). Parce que\(2^n≥2\) pour tous\(n≥1\), la séquence est limitée en dessous. Cependant, la séquence n'est pas bornée au-dessus. Il s'\(\left\{2^n\right\}\)agit donc d'une séquence illimitée.
Nous discutons maintenant de la relation entre les limites et la convergence. Supposons qu'\(\{a_n\}\)une séquence soit illimitée. Il n'est alors pas limité au-dessus, ni en dessous, ni les deux. Dans les deux cas, il existe des termes dont l'ampleur est arbitrairement grande au fur et à mesure qu'ils\(n\) s'agrandissent. Par conséquent, la séquence\(\{a_n\}\) ne peut pas converger. Par conséquent, être limité est une condition nécessaire pour qu'une séquence converge.
Si une séquence\(\{a_n\}\) converge, elle est bornée.
Notez qu'une séquence délimitée n'est pas une condition suffisante pour qu'une séquence converge. Par exemple, la séquence\(\left\{(−1)^n\right\}\) est bornée, mais elle diverge parce que la séquence oscille entre\(1\)\(−1\) et ne s'approche jamais d'un nombre fini. Nous discutons maintenant d'une condition suffisante (mais non nécessaire) pour qu'une séquence bornée converge.
Prenons l'exemple d'une séquence bornée\(\{a_n\}\). Supposons que la séquence\(\{a_n\}\) augmente. C'est-à-dire que\(a_1≤a_2≤a_3….\) puisque la séquence augmente, les termes n'oscillent pas. Il existe donc deux possibilités. La séquence peut diverger à l'infini ou converger. Cependant, comme la séquence est bornée, elle est bornée au-dessus et la séquence ne peut pas diverger à l'infini. Nous en concluons que cela\(\{a_n\}\) converge. Par exemple, considérez la séquence
\[\left\{\dfrac{1}{2},\,\dfrac{2}{3},\,\dfrac{3}{4},\,\dfrac{4}{5},\,…\right\}. \nonumber \]
Comme cette séquence augmente et se limite au-dessus, elle converge. Ensuite, considérez la séquence
\[\left\{2,\,0,\,3,\,0,\,4,\,0,\,1,\,−\dfrac{1}{2},\,−\dfrac{1}{3},\,−\dfrac{1}{4},\,…\right\}. \nonumber \]
Même si la séquence n'augmente pas pour toutes les valeurs de\(n\), nous le constatons\(−1/2<−1/3<−1/4<⋯\). Par conséquent, à partir du huitième terme\(a_8=−1/2\), la séquence augmente. Dans ce cas, nous disons que la séquence finit par augmenter. Comme la séquence est bornée au-dessus, elle converge. Il est également vrai que si une séquence est décroissante (ou finalement décroissante) et bornée en dessous, elle converge également.
Une séquence\(\{a_n\}\) augmente pour tous\(n≥n_0\) si
\(a_n≤a_{n+1}\)pour tous\(n≥n_0\).
Une séquence\(\{a_n\}\) est décroissante pour tous\(n≥n_0\) si
\(a_n ≥ a_{n+1}\)pour tous\(n≥n_0\).
Une séquence\(\{a_n\}\) est une séquence monotone pour tous\(n≥n_0\) si elle augmente pour tous\(n≥n_0\) ou diminue pour tous\(n≥n_0\).
Nous avons maintenant les définitions nécessaires pour énoncer le théorème de convergence monotone, qui donne une condition suffisante pour la convergence d'une séquence.
S'il s'\(\{a_n\}\)agit d'une séquence bornée et qu'il existe un entier positif\(n_0\) tel qu'il\(\{a_n\}\) soit monotone pour tous\(n≥n_0\), alors\(\{a_n\}\) converge.
La preuve de ce théorème dépasse le cadre de ce texte. Au lieu de cela, nous fournissons un graphique pour montrer intuitivement pourquoi ce théorème a du sens (Figure\(\PageIndex{6}\)).
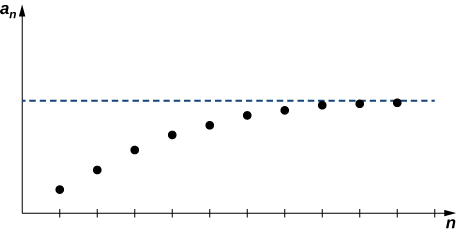
Dans l'exemple suivant, nous montrons comment le théorème de convergence monotone peut être utilisé pour prouver la convergence d'une séquence.
Pour chacune des séquences suivantes, utilisez le théorème de convergence monotone pour montrer que la séquence converge et déterminer sa limite.
- \(\left\{\dfrac{4^n}{n!}\right\}\)
- \(\{a_n\}\)défini de manière récursive de telle sorte que
\(a_1=2\) et\(a_{n+1}=\dfrac{a_n}{2}+\dfrac{1}{2a_n}\) pour tous\(n≥2.\)
Solution
a. En rédigeant les premiers termes, on constate que
\(\left\{\dfrac{4^n}{n!}\right\}=\left\{4,\,8,\,\dfrac{32}{3},\,\dfrac{32}{3},\,\dfrac{128}{15},\,…\right\}.\)
Dans un premier temps, les termes augmentent. Toutefois, après le troisième mandat, les durées diminuent. En fait, les termes diminuent pour tous\(n≥3\). Nous pouvons le montrer comme suit.
\(a_{n+1}=\dfrac{4^{n+1}}{(n+1)!}=\dfrac{4}{n+1}⋅\dfrac{4^n}{n!}=\dfrac{4}{n+1}⋅a_n≤a_n\)si\(n≥3.\)
Par conséquent, la séquence est décroissante pour tous\(n≥3\). De plus, la séquence est limitée en dessous par\(0\) parce que\(4n/n!≥0\) pour tous les entiers positifs\(n\). Par conséquent, selon le théorème de convergence monotone, la séquence converge.
Pour trouver la limite, nous utilisons le fait que la séquence converge et laisse\(\displaystyle L=\lim_{n→∞}a_n\). Notez maintenant cette observation importante. Considérez\(\displaystyle \lim_{n→∞}a_{n+1}\). Depuis
\(\{a_{n+1}\}=\{a_2,\,a_3,\,a_4,\,…\},\)
la seule différence entre les séquences\(\{a_{n+1}\}\) et\(\{a_n\}\) est que le premier terme\(\{a_{n+1}\}\) n'est pas pris en compte. Comme un nombre fini de termes n'affecte pas la convergence d'une séquence,
\(\displaystyle \lim_{n→∞}a_{n+1}=\lim_{n→∞}a_n=L.\)
Combiner ce fait avec l'équation
\(a_{n+1}=\dfrac{4}{n+1}a_n\)
et en prenant la limite des deux côtés de l'équation
\(\displaystyle \lim_{n→∞}a_{n+1}=\lim_{n→∞}\dfrac{4}{n+1}a_n\),
nous pouvons en conclure que
\(L=0⋅L=0.\)
b. Rédaction des premiers termes,
\(\left\{2,\,\dfrac{5}{4},\,\dfrac{41}{40},\,\dfrac{3281}{3280},\,…\right\}.\)
on peut supposer que la séquence est décroissante et bornée en dessous de\(1\). Pour montrer que la séquence est limitée en dessous par\(1\), nous pouvons montrer que
\(\dfrac{a_n}{2}+\dfrac{1}{2a_n}≥1.\)
Pour le montrer, commencez par réécrire
\(\dfrac{a_n}{2}+\dfrac{1}{2a_n}=\dfrac{a^2_n+1}{2a_n}\).
Puisque\(a_1>0\) et\(a_2\) est défini comme une somme de termes positifs, de\(a_2>0.\) même, tous les termes\(a_n>0\). Par conséquent,
\(\dfrac{a^2n+1}{2a_n}≥1\)
si et seulement si
\(a^2_n+1≥2a_n\).
Réécrire l'inégalité\(a^2_n+1≥2a_n\)\(a^2_n−2a_n+1≥0\) en utilisant le fait que
\(a^2_n−2a_n+1=(a_n−1)^2≥0\)
parce que le carré de tout nombre réel n'est pas négatif, nous pouvons en conclure que
\(\dfrac{a^n}{2}+\dfrac{1}{2a_n}≥1.\)
Pour montrer que la séquence est décroissante, nous devons le montrer\(a_{n+1}≤a_n\) pour tous\(n≥1\). Depuis\(1≤a^2_n\), il s'ensuit que
\(a^2_n+1≤2a^2_n\).
En divisant les deux côtés par\(2a_n\), on obtient
\(\dfrac{a_n}{2}+\dfrac{1}{2a_n}≤a_n.\)
En utilisant la définition de\(a_{n+1}\), nous concluons que
\(a_{n+1}=\dfrac{a_n}{2}+\dfrac{1}{2a_n}≤a_n\).
Comme\(\{a_n\}\) il est limité en dessous et décroissant, par le théorème de convergence monotone, il converge.
Pour trouver la limite, laissez\(\displaystyle L=\lim_{n→∞}a_n\). Ensuite, en utilisant la relation de récurrence et le fait que\(\displaystyle \lim_{n→∞}a_n=\lim_{n→∞}a_{n+1}\), nous avons
\(\displaystyle \lim_{n→∞}a_{n+1}=\lim_{n→∞}(\dfrac{a_n}{2}+\dfrac{1}{2a_n})\),
et donc
\(L=\dfrac{L}{2}+\dfrac{1}{2L}\).
En multipliant les deux côtés de cette équation par\(2L\), nous arrivons à l'équation
\(2L^2=L^2+1\).
En résolvant cette équation,\(L,\) nous concluons que\(L^2=1\), ce qui implique\(L=±1\). Puisque tous les termes sont positifs, la limite\(L=1\).
Considérez la séquence\(\{a_n\}\) définie de manière récursive telle que\(a_1=1\),\(a_n=a_{n−1}/2\). Utilisez le théorème de convergence monotone pour montrer que cette séquence converge et trouve sa limite.
- Allusion
-
Afficher que la séquence est décroissante et bornée en dessous.
- Réponse
-
\(0\).
Les nombres de Fibonacci sont définis de manière récursive par la séquence\(\left\{F_n\right\}\) où\(F_0=0, \, F_1=1\) et pour\(n≥2,\)
\(F_n=F_{n−1}+F_{n−2}.\)
Nous examinons ici les propriétés des nombres de Fibonacci.
1. Écrivez les vingt premiers nombres de Fibonacci.
2. Trouvez une formule fermée pour la séquence de Fibonacci en suivant les étapes suivantes.
a. Considérez la séquence définie de manière récursive\({x_n}\) où\(x_0=c\) et\(x_{n+1}=ax_n\). Montrez que cette séquence peut être décrite par la formule fermée\(x_n=ca^n\) pour tous\(n≥0.\)
b. En utilisant le résultat de la partie a. comme motivation, recherchez une solution de l'équation
\(F_n=F_{n−1}+F_{n−2}\)
du formulaire\(F_n=cλ^n\). Déterminez pour quoi deux valeurs\(λ\) permettront\(F_n\) de satisfaire cette équation.
c. Examinez les deux solutions de la partie b. :\(λ_1\) et\(λ_2\). Laissez\(F_n=c_1λ_1^n+c_2λ_2^n\). Utilisez les conditions initiales\(F_0\) et\(F_1\) déterminez les valeurs des constantes\(c_1\)\(c_2\) et écrivez la formule fermée\(F_n\).
3. Utilisez la réponse en 2 c. pour montrer que
\[\lim_{n→∞}\dfrac{F_{n+1}}{F_n}=\dfrac{1+\sqrt{5}}{2}.\nonumber \]
Le nombre\(ϕ=(1+\sqrt{5})/2\) est connu sous le nom de nombre d'or (Figure et Figure).


Concepts clés
- Pour déterminer la convergence d'une séquence donnée par une formule explicite\(a_n=f(n)\), nous utilisons les propriétés des limites des fonctions.
- Si\(\{a_n\}\) et\(\{b_n\}\) sont des séquences convergentes qui convergent vers\(A\) et\(B,\) respectivement, et\(c\) est un nombre réel quelconque, alors\(c\cdot A,\) la séquence\(\{ca_n\} \)\(\{a_n±b_n\}\) converge vers\(A±B,\) les séquences\(\{a_n\cdot b_n\}\) convergent vers\(A⋅B,\) et la séquence\(\{a_n/b_n\}\) converge vers la séquence\(A/B,\) fournie\(B≠0.\)
- Si une séquence est bornée et monotone, elle converge, mais toutes les séquences convergentes ne sont pas monotones.
- Si une séquence est illimitée, elle diverge, mais toutes les séquences divergentes ne sont pas illimitées.
- La séquence géométrique\(\left\{r^n\right\}\) converge si et seulement si\(|r|<1\) ou\(r=1\).
Lexique
- séquence arithmétique
- une séquence dans laquelle la différence entre chaque paire de termes consécutifs est la même est appelée séquence arithmétique
- délimité au-dessus
- une séquence\(\{a_n\}\) est bornée au-dessus s'il existe une constante\(M\) telle que\(a_n≤M\) pour tous les entiers positifs\(n\)
- borné en dessous
- une séquence\(\{a_n\}\) est bornée en dessous s'il existe une constante\(M\) telle que\(M≤a_n\) pour tous les entiers positifs\(n\)
- séquence bornée
- une séquence\(\{a_n\}\) est bornée s'il existe une constante\(M\) telle que\(|a_n|≤M\) pour tous les entiers positifs\(n\)
- séquence convergente
- une séquence convergente est une séquence\(\{a_n\}\) pour laquelle il existe un nombre réel\(L\) tel qu'il\(a_n\) est arbitrairement proche\(L\) tant qu'\(n\)il est suffisamment grand
- séquence divergente
- une séquence qui n'est pas convergente est divergente
- formule explicite
- une séquence peut être définie par une formule explicite telle que\(a_n=f(n)\)
- séquence géométrique
- une séquence\(\{a_n\}\) dans laquelle le rapport\(a_{n+1}/a_n\) est le même pour tous les entiers positifs\(n\) est appelée séquence géométrique
- variable d'indice
- l'indice utilisé pour définir les termes d'une séquence est appelé index
- limite d'une séquence
- le nombre réel\(L\) vers lequel une séquence converge s'appelle la limite de la séquence
- séquence monotone
- une séquence croissante ou décroissante
- relation de récidive
- une relation de récurrence est une relation dans laquelle un terme\(a_n\) d'une séquence est défini en fonction de termes antérieurs de la séquence
- séquence
- une liste ordonnée de numéros de la forme\(a_1,\,a_2,\,a_3,\,…\) est une séquence
- terme
- le nombre\(a_n\) de la séquence\(\{a_n\}\) est appelé le\(n^{\text{th}}\) terme de la séquence
- séquence illimitée
- une séquence qui n'est pas bornée est appelée illimitée


