9.2E : Exercices pour la section 9.2

Last updated
Save as PDF

Page ID: 197725

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Dans les exercices 1 à 4, utilisez la notation sigma pour écrire chaque expression sous la forme d'une série infinie.

1)$1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+⋯$

Réponse: $\displaystyle \sum_{n=1}^∞\frac{1}{n}$

2)$ 1−1+1−1+⋯$

3)$ 1−\frac{1}{2}+\frac{1}{3}−\frac{1}{4}+...$

Réponse: $\displaystyle \sum_{n=1}^∞\frac{(−1)^{n−1}}{n}$

4)$ \sin 1+\sin \frac{1}{2}+\sin \frac{1}{3}+\sin \frac{1}{4}+⋯$

Dans les exercices 5 à 8, calculez les quatre premières sommes partielles$ S_1,…,S_4$ de la série dont le$ n^{\text{th}}$ terme$ a_n$ commence par$ n=1$ ce qui suit.

5)$ a_n=n$

Réponse: $ 1,3,6,10$

6)$ a_n=1/n$

7)$ a_n=\sin \frac{nπ}{2}$

Réponse: $ 1,1,0,0$

8)$ a_n=(−1)^n$

Dans les exercices 9 à 12, calculez le terme général$ a_n$ de la série avec la somme partielle donnée$ S_n$. Si la séquence de sommes partielles converge, trouvez sa limite$ S$.

9)$ S_n=1−\frac{1}{n}, \quad n≥2$

Réponse: $ a_n=S_n−S_{n−1}=\dfrac{1}{n−1}−\dfrac{1}{n}.$Puisque$\displaystyle S = \lim_{n\to\infty} S_n = \lim_{n\to\infty} \left(1−\frac{1}{n}\right) = 1,$ la série converge vers$ S=1.$

10)$ S_n=\dfrac{n(n+1)}{2}, \quad n≥1$

11)$ S_n=\sqrt{n},\quad n≥2$

Réponse: $ a_n=S_n−S_{n−1}=\sqrt{n}−\sqrt{n−1}=\dfrac{1}{\sqrt{n−1}+\sqrt{n}}.$
La série diverge parce que les sommes partielles ne sont pas bornées.
C'est-à-dire$\displaystyle \lim_{n\to\infty} S_n = \lim_{n\to\infty} \sqrt{n} = \infty.$

(12)$ S_n=2−\dfrac{n+2}{2^n},\quad n≥1$

Pour chaque série des exercices 13 à 16, utilisez la séquence de sommes partielles afin de déterminer si la série converge ou diverge.

13)$\displaystyle \sum_{n=1}^∞\frac{n}{n+2}$

Réponse: $ S_1=1/3,$
$ S_2=1/3+2/4>1/3+1/3=2/3,$
$S_3=1/3+2/4+3/5>3⋅(1/3)=1.$
En général$ S_k>k/3,$, la série diverge.
Notez que le$n^{\text{th}}$ Term Test for Divergence pourrait également être utilisé pour prouver que cette série diverge.

(14)$\displaystyle \sum_{n=1}^∞(1−(−1)^n))$

15)$\displaystyle \sum_{n=1}^∞\frac{1}{(n+1)(n+2)}$$\quad\Big($ Conseil : utilisez une décomposition par fraction partielle comme celle-ci pour$\displaystyle \sum_{n=1}^∞\frac{1}{n(n+1)}.\Big)$

Réponse

$ S_1=1/(2\cdot 3)=1/6=2/3−1/2,$

$ S_2=1/(2\cdot 3)+1/(3\cdot 4)=2/12+1/12=1/4=3/4−1/2,$

$ S_3=1/(2\cdot 3)+1/(3\cdot 4)+1/(4\cdot 5)=10/60+5/60+3/60=3/10=4/5−1/2,$

$ S_4=1/(2\cdot 3)+1/(3\cdot 4)+1/(4\cdot 5)+1/(5\cdot 6)=10/60+5/60+3/60+2/60=1/3=5/6−1/2.$

Le modèle est$ S_k=\dfrac{k+1}{k+2}−\dfrac{1}{2}.$
alors, de$\displaystyle \lim_{n\to\infty} S_n = \lim_{n\to\infty} \left( \dfrac{k+1}{k+2}−\dfrac{1}{2} \right) = \dfrac{1}{2},$ sorte que la série converge vers$ 1/2.$

16)$\displaystyle \sum_{n=1}^∞\frac{1}{2n+1}$$\quad\Big($ Conseil : Suivez le raisonnement de$\displaystyle \sum_{n=1}^∞\frac{1}{n}.\Big)$

Supposons que$\displaystyle \sum_{n=1}^∞a_n=1$, cela$\displaystyle \sum_{n=1}^∞b_n=−1$$ a_1=2$, cela et$ b_1=−3$. Utilisez ces informations pour trouver la somme des séries indiquées dans les exercices 17 à 20.

17)$\displaystyle \sum_{n=1}^∞(a_n+b_n)$

Réponse: $ \displaystyle \sum_{n=1}^∞(a_n+b_n) \quad = \quad \sum_{n=1}^∞ a_n + \sum_{n=1}^∞ b_n \quad = \quad 1 + (-1) \quad = \quad 0$

18)$\displaystyle \sum_{n=1}^∞(a_n−2b_n)$

19)$\displaystyle \sum_{n=2}^∞(a_n−b_n)$

Réponse: $\displaystyle \sum_{n=2}^∞(a_n−b_n) \quad = \quad \sum_{n=2}^∞ a_n - \sum_{n=2}^∞ b_n \quad = \quad \left(\sum_{n=1}^∞ a_n - a_1\right) - \left(\sum_{n=1}^∞ b_n -b_1\right) \quad = \quad (1 - 2) - (-1 - (-3)) = -1 - 2 \quad = \quad -3$

(20)$\displaystyle \sum_{n=1}^∞(3a_{n+1}−4b_{n+1})$

Dans les exercices 21 à 26, indiquez si la série donnée converge ou diverge et expliquez pourquoi.

21)$\displaystyle \sum_{n=1}^∞\frac{1}{n+1000}$ (Astuce : réécrivez en modifiant l'index.)

Réponse: La série diverge,$\displaystyle \sum_{n=1001}^∞\frac{1}{n}$

22)$\displaystyle \sum_{n=1}^∞\frac{1}{n+10^{80}}$ (Astuce : réécrivez en modifiant l'index.)

23)$ 1+\frac{1}{10}+\frac{1}{100}+\frac{1}{1000}+⋯$

Réponse: Il s'agit d'une série géométrique convergente, puisque$ r=\frac{1}{10}<1$

(24)$ 1+\frac{e}{π}+\frac{e^2}{π^2}+\frac{e^3}{π^3}+⋯$

25)$ 1+\frac{π}{e^2}+\frac{π^2}{e^4}+\frac{π^3}{e^6}+\frac{π^4}{e^8}+⋯$

Réponse: Il s'agit d'une série géométrique convergente, puisque$ r=π/e^2<1$

26)$ 1−\sqrt{\frac{π}{3}}+\sqrt{\frac{π^2}{9}}−\sqrt{\frac{π^3}{27}}+⋯$

Pour chacun des exercices 27$ a_n$ à 30, écrivez sa somme sous la forme d'une série géométrique de la forme$\displaystyle \sum_{n=1}^∞ar^n$. Indiquez si la série converge et, si c'est le cas, trouvez la valeur exacte de sa somme.

27)$ a_1=−1$ et$ \dfrac{a_n}{a_{n+1}}=−5$ pour$ n≥1.$

Réponse: $\displaystyle \sum_{n=1}^∞5⋅(−1/5)^n$, converge vers$ −5/6$

28)$ a_1=2$ et$ \dfrac{a_n}{a_{n+1}}=1/2$ pour$ n≥1.$

29)$ a_1=10$ et$ \dfrac{a_n}{a_{n+1}}=10$ pour$ n≥1$.

Réponse: $\displaystyle \sum_{n=1}^∞100⋅(1/10)^n,$converge vers$\frac{100}{9}$

30)$ a_1=\frac{1}{10}$ et$ a_n/a_{n+1}=−10$ pour$ n≥1$.

Dans les exercices 31 à 34, utilisez l'identité$\displaystyle \frac{1}{1−y}=\sum_{n=0}^∞y^n$ (qui est vraie pour$|y| < 1$) pour exprimer chaque fonction sous la forme d'une série géométrique dans le terme indiqué.

31)$ \dfrac{x}{1+x}$ dans$ x$

Réponse: $\displaystyle x\sum_{n=0}^∞(−x)^n=\sum_{n=1}^∞(−1)^{n−1}x^n$

32)$ \dfrac{\sqrt{x}}{1−x^{3/2}}$ dans$ \sqrt{x}$

33)$ \dfrac{1}{1+\sin^2x}$ dans$\sin x$

Réponse: $\displaystyle \sum_{n=0}^∞(−1)^n\sin^{2n}(x)$

34)$ \sec^2 x$ dans$\sin x$

Dans les exercices 35 à 38, évaluez la série télescopique ou déterminez si la série diverge.

35)$\displaystyle \sum_{n=1}^∞2^{1/n}−2^{1/(n+1)}$

Réponse: $ S_k=2−2^{1/(k+1)}→1$comme$ k→∞.$

36)$\displaystyle \sum_{n=1}^∞\frac{1}{n^{13}}−\frac{1}{(n+1)^{13}}$

(37)$\displaystyle \sum_{n=1}^∞(\sqrt{n}−\sqrt{n+1})$

Réponse: $ S_k=1−\sqrt{k+1}$diverge

38)$\displaystyle \sum_{n=1}^∞(\sin n−\sin(n+1))$

Exprimez chaque série des exercices 39 à 42 sous la forme d'une somme télescopique et évaluez sa somme$n^{\text{th}}$ partielle.

39)$\displaystyle \sum_{n=1}^∞\ln\left(\frac{n}{n+1}\right)$

Réponse: $\displaystyle \sum_{n=1}^∞[\ln n−\ln(n+1)],$
$S_k=−\ln(k+1)$

40)$\displaystyle \sum_{n=1}^∞\frac{2n+1}{(n^2+n)^2}$ (Conseil : dénominateur factoriel et utilisation de fractions partielles.)

41)$\displaystyle \sum_{n=2}^∞\frac{\ln\left(1+\frac{1}{n}\right)}{(\ln n)\ln(n+1)}$

Réponse: $ a_n=\frac{1}{\ln n}−\frac{1}{\ln(n+1)}$et$ S_k=\frac{1}{\ln(2)}−\frac{1}{\ln(k+1)}→\frac{1}{\ln(2)}$

42)$\displaystyle \sum_{n=1}^∞\frac{(n+2)}{n(n+1)2^{n+1}}$ (Indice : Regardez$ 1/(n2^n)$.

Une série télescopique générale est une série dans laquelle tous les termes, sauf les premiers, s'annulent après avoir additionné un certain nombre de termes successifs.

43) Laissez$ a_n=f(n)−2f(n+1)+f(n+2),$ entrer ce$ f(n)→0$ que$ n→∞.$ Find$\displaystyle \sum_{n=1}^∞a_n$.

Réponse: $\displaystyle \sum_{n=1}^∞a_n=f(1)−f(2)$

44)$ a_n=f(n)−f(n+1)−f(n+2)+f(n+3),$ dans lequel$ f(n)→0$ comme$ n→∞$. Trouve$\displaystyle \sum_{n=1}^∞a_n$.

45) Supposons que l'$ a_n=c_0f(n)+c_1f(n+1)+c_2f(n+2)+c_3f(n+3)+c_4f(n+4),$endroit où$ f(n)→0$ se trouve$ n→∞$. Trouvez une condition sur les coefficients$ c_0,…,c_4$ qui en fait une série télescopique générale.

Réponse: $ c_0+c_1+c_2+c_3+c_4=0$

46) Évaluer$\displaystyle \sum_{n=1}^∞\frac{1}{n(n+1)(n+2)}$ (Astuce :$\displaystyle \frac{1}{n(n+1)(n+2)}=\frac{1}{2n}−\frac{1}{n+1}+\frac{1}{2(n+2)}$)

47) Évaluer$\displaystyle \sum_{n=2}^∞\frac{2}{n^3−n}.$

Réponse: $\displaystyle \frac{2}{n^3−1}=\frac{1}{n−1}−\frac{2}{n}+\frac{1}{n+1},$
$S_n=(1−1+1/3)+(1/2−2/3+1/4) +(1/3−2/4+1/5)+(1/4−2/5+1/6)+⋯=1/2$

48) Trouvez une formule pour$\displaystyle \sum_{n=1}^∞\frac{1}{n(n+N)}$ où$ N$ est un entier positif.

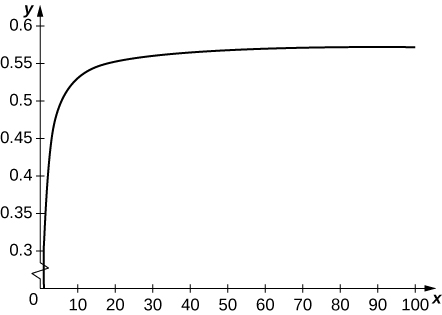
49) [T] Définissez une séquence$\displaystyle t_k=\sum_{n=1}^{k−1}(1/k)−\ln k$. Utilisez le graphique de$ 1/x$ pour vérifier qu'il s'$ t_k$agit d'une augmentation. $ t_k$Tracez$ k=1…100$ et indiquez s'il apparaît que la séquence converge.

Réponse

$ t_k$converge vers$ 0.57721…t_k$ est la somme des rectangles de hauteur$ 1/k$ sur l'intervalle$ [k,k+1]$ situé au-dessus du graphique de$ 1/x$.

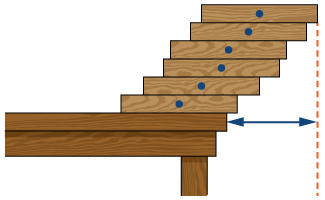
50) [T] Supposons que des blocs rectangulaires uniformes et$ N$ égaux soient empilés les uns sur les autres, ce qui permet un certain surplomb. La loi du levier d'Archimède implique que l'empilement de$ N$ blocs est stable tant que le centre de gravité des$ (N−1)$ blocs supérieurs se trouve au bord du bloc inférieur. $ x$Dénotons la position du bord du bloc inférieur et considérez sa position par rapport au centre du bloc le plus proche du bas. Cela implique que$ (N−1)x=\left(\frac{1}{2}−x\right)$ ou$ x=1/(2N)$. Utilisez cette expression pour calculer le surplomb maximal (la position du bord du bloc supérieur par rapport au bord du bloc inférieur). Reportez-vous à la figure suivante.

Chacune des séries infinies suivantes converge vers le multiple donné de$ π$ ou$ 1/π$.

Dans chaque cas, déterminez la valeur minimale de$ N$ telle sorte que la somme$ Nth$ partielle de la série se rapproche exactement du côté gauche du nombre de décimales donné, et donnez la valeur approximative souhaitée. Jusqu'à la$ 15$ décimale,$ π=3.141592653589793....$

51) [T]$\displaystyle π=−3+\sum_{n=1}^∞\frac{n2^nn!^2}{(2n)!},$ erreur$ <0.0001$

Réponse: $N=22,$
$S_N=6.1415$

52) [T]$\displaystyle \frac{π}{2}=\sum_{k=0}^∞\frac{k!}{(2k+1)!!}=\sum_{k=0}^∞\frac{2^kk!^2}{(2k+1)!},$ erreur$ <10^{−4}$

53) [T]$\displaystyle \frac{9801}{2π}=\frac{4}{9801}\sum_{k=0}^∞\frac{(4k)!(1103+26390k)}{(k!)^4396^{4k}},$ erreur$ <10^{−12}$

Réponse: $ N=3,$
$S_N=1.559877597243667...$

54) [T]$\displaystyle \frac{1}{12π}=\sum_{k=0}^∞\frac{(−1)^k(6k)!(13591409+545140134k)}{(3k)!(k!)^3640320^{3k+3/2}}$, erreur$ <10^{−15}$

55) [T] Une pièce équitable est une pièce qui a une probabilité$ 1/2$ de faire monter des têtes lorsqu'elle est retournée.

a. Quelle est la probabilité qu'une pièce juste apparaisse deux$ n$ fois de suite ?

b. Déterminez la probabilité qu'une pièce se retrouve face à face pour la première fois après un nombre pair de lancements de pièces.

Réponse: a. La probabilité d'une séquence ordonnée donnée de résultats pour les lancements de$ n$ pièces est de$ 1/2^n$.
b. La probabilité de faire face pour la première fois au dernier retournement est la probabilité de la séquence$ TT…TH$ qui est$ 1/2^n$.$ n$ La probabilité de se retrouver tête pour la première fois sur un flip pair est de$\displaystyle \sum_{n=1}^∞1/2^{2n}$ ou$ 1/3$.

56) [T] Détermine la probabilité qu'une pièce soit retournée un multiple de trois fois avant de se heurter à des têtes.

57) [T] Déterminez la probabilité qu'une pièce juste se retrouve face à face pour la deuxième fois après un nombre pair de retournements.

Réponse: $5/9$

58) [T] Trouvez une série qui exprime la probabilité qu'une pièce juste se retrouve face à face pour la deuxième fois sur un multiple de trois retournements.

59) [T] Le nombre attendu de fois qu'une pièce équitable se heurte à des têtes est défini comme la somme$ n=1,2,…$ des$ n$ fois de la probabilité que la pièce apparaisse exactement$ n$ fois de suite, ou$ \dfrac{n}{2^{n+1}}$. Calculez le nombre attendu de fois consécutives qu'une pièce de monnaie équitable apparaîtra.

Réponse: $\displaystyle E=\sum_{n=1}^∞\frac{n}{2^{n+1}}=1,$comme on peut le montrer en utilisant la sommation par parties

60) [T] Une personne fait des dépôts$ $10$ au début de chaque trimestre sur un compte bancaire qui rapporte des intérêts$ 4%$ annuels composés trimestriellement (quatre fois par an).

a. Démontrer que les intérêts accumulés après les$ n$ trimestres sont$ $10(\frac{1.01^{n+1}−1}{0.01}−n).$

b. Trouvez les huit premiers termes de la séquence.

c. Quel est le montant des intérêts accumulés après des$ 2$ années ?

61) [T] Supposons que la quantité d'un médicament dans le système d'un patient diminue d'un facteur multiplicatif$ r<1$ chaque heure. Supposons qu'une nouvelle dose soit administrée toutes les$ N$ heures. Trouvez une expression qui donne la quantité$ A(n)$ dans le système du patient après$ n$ quelques heures pour chacun$ n$ en termes de dosage$ d$ et de ratio$ r$. (Conseil : écrivez$ n=mN+k$ où$ 0≤k<N$ et additionnez les valeurs des différentes doses administrées.)

Réponse: La partie de la première dose après les$ n$ heures de travail est$ dr^n$, la partie de la deuxième dose est$ dr^{n−N}$, et, en général, la partie restante de la$ m^{\text{th}}$ dose est$ dr^{n−mN}$$\displaystyle A(n)=\sum_{l=0}^mdr^{n−lN}=\sum_{l=0}^mdr^{k+(m−l)N}=\sum_{q=0}^mdr^{k+qN}=dr^k\sum_{q=0}^mr^{Nq}=dr^k\frac{1−r^{(m+1)N}}{1−r^N},\;\text{where}\,n=k+mN.$

62) [T] Un certain médicament n'est efficace pour un patient moyen que s'il y a au moins$ 1$ mg par kg dans le système du patient, alors qu'il n'est sûr que s'il y en a au plus en$ 2$ mg par kg dans le système d'un patient moyen. Supposons que la quantité dans le système d'un patient diminue d'un facteur multiplicatif$ 0.9$ chaque heure après l'administration d'une dose. Déterminez l'intervalle maximal$ N$ d'heures entre les doses et la fourchette de doses correspondante$ d$ (en mg/kg) pour$ N$ cela, qui permettra d'utiliser le médicament à la fois sans danger et efficace à long terme.

63) Supposons qu'il$ a_n≥0$ s'agisse d'une séquence de chiffres. Expliquez pourquoi la séquence des sommes partielles de$ a_n$ augmente.

Réponse: $ S_{N+1}=a_{N+1}+S_N≥S_N$

64) [T] Supposons qu'il$ a_n$ s'agisse d'une séquence de nombres positifs et que la séquence$ S_n$ de sommes partielles de$ a_n$ soit bornée au-dessus. Expliquez pourquoi les$\displaystyle \sum_{n=1}^∞a_n$ convergent. La conclusion restera-t-elle vraie si nous supprimons l'hypothèse$ a_n≥0$ ?

65) [T] Supposons que$ a_1=S_1=1$ et que, pour des nombres$ S>1$ et des nombres donnés$ 0<k<1$, on définit$ a_{n+1}=k(S−S_n)$ et$ S_{n+1}=a_{n+1}+S_n$. Est-ce que cela$ S_n$ converge ? Si c'est le cas, vers quoi ? (Astuce : faites d'abord valoir que cela vaut$ S_n<S$ pour tous$ n$ et qu'$ S_n$il augmente.)

Réponse: Depuis$ S>1, a_2>0,$ et depuis$ k<1, S_2=1+a_2<1+(S−1)=S$. Si$ S_n>S$ pour certains$ n$, il y en a un plus petit$ n$. Pour cela$ n, S>S_{n−1}$, il y$ S_n=S_{n−1}+k(S−S_{n−1})=kS+(1−k)S_{n−1}<S$ a donc une contradiction. Ainsi$ S_n<S$ et$ a_{n+1}>0$ pour tous$ n$, il en$ S_n$ va de même pour l'augmentation et les limites$ S$. Laissez$\displaystyle S_∗=\lim S_n$. Si$ S_∗<S$, alors$ δ=k(S−S_∗)>0$, mais nous pouvons trouver n tel que$ S_∗−S_n<δ/2$, ce qui implique que$ S_{n+1}=S_n+k(S−S_n) >S_∗+δ/2$, contredisant que Sn augmente à$ S_∗$. Ainsi$ S_n→S.$

66) [T] Une version de la croissance de von Bertalanffy peut être utilisée pour estimer l'âge d'un individu d'une espèce homogène à partir de sa longueur si l'augmentation annuelle est$ n+1$ satisfaisante$ a_{n+1}=k(S−S_n)$, avec$ S_n$$ n, S$ comme longueur annuelle comme longueur limite, et$ k$ comme constante de croissance relative. Si$ S_1=3, S=9,$ et estimez$ k=1/2,$ numériquement la plus petite valeur de n telle que$ S_n≥8$. Notez que$ S_{n+1}=S_n+a_{n+1}.$ Trouvez le$ n$ moment correspondant$ k=1/4.$

67) [T] Supposons qu'il$\displaystyle \sum_{n=1}^∞a_n$ s'agisse d'une série convergente de termes positifs. Expliquez pourquoi$\displaystyle \lim_{N→∞}\sum_{n=N+1}^∞a_n=0.$

Réponse: Laissez$\displaystyle S_k=\sum_{n=1}^ka_n$ et$ S_k→L$. Puis$ S_k$ finit par devenir arbitrairement proche de$ L$, ce qui signifie que cela$\displaystyle L−S_N=\sum_{n=N+1}^∞a_n$ devient arbitrairement petit comme$ N→∞.$

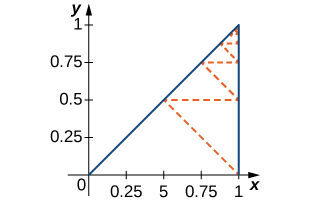
68) [T] Détermine la longueur de la trajectoire en zig-zag en pointillés dans la figure suivante.

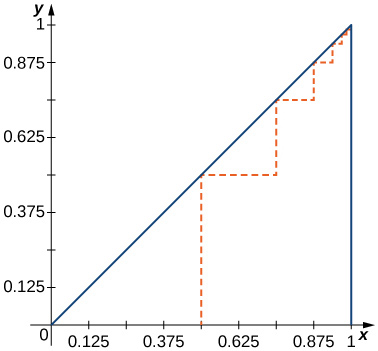
69) [T] Déterminez la longueur totale du tracé en pointillés dans la figure suivante.

Réponse: $\displaystyle L=\left(1+\frac{1}{2}\right)\sum_{n=1}^∞\frac{1}{2^n}=\frac{3}{2}$.

70) [T] Le triangle de Sierpinski est obtenu à partir d'un triangle en supprimant le quart central comme indiqué à la première étape, en supprimant les quarts médians des trois triangles congruents restants à la deuxième étape et, en général, en supprimant les quarts médians des triangles restants dans chaque étape successive. En supposant que le triangle d'origine est représenté sur la figure, trouvez les aires des parties restantes du triangle d'origine après les$ N$ étapes et déterminez la longueur totale de tous les triangles limites après les$ N$ étapes.

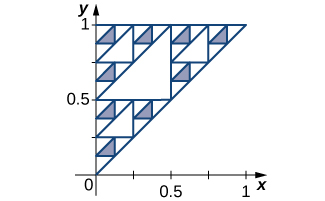
71) [T] Le joint de Sierpinski est obtenu en divisant le carré unitaire en neuf sous-carrés égaux, en supprimant le carré du milieu, puis en faisant de même à chaque étape pour les sous-carrés restants. La figure montre l'ensemble restant après quatre itérations. Calculez la surface totale supprimée après$ N$ les étapes et calculez la longueur du périmètre total de l'ensemble restant après$ N$ les étapes.

Réponse: Au premier stade, un carré de surface$ 1/9$ est supprimé, au$ 2$ premier stade, des$ 8$ carrés de surface$ 1/9^2$, au troisième, on supprime des$ 8^2$ carrés de surface$ 1/9^3$, et ainsi de suite. La surface totale enlevée après$ N$ les étapes est$N→∞.$ la$\displaystyle \sum_{n=0}^{N−1}\frac{8^N}{9^{N+1}}=\frac{1}{8}\cdot\frac{1−(8/9)^N}{1−8/9}→1$ suivante : Le périmètre total est$\displaystyle 4+4\sum_{n=0}^∞\frac{8^N}{3^{N+1}}→∞.$