3.2 : La dérivée en tant que fonction
- Page ID
- 197874
- Définissez la fonction dérivée d'une fonction donnée.
- Tracez une fonction dérivée à partir du graphe d'une fonction donnée.
- Indiquez le lien entre les dérivées et la continuité.
- Décrivez trois conditions lorsqu'une fonction ne possède pas de dérivée.
- Expliquez la signification d'une dérivée d'ordre supérieur.
Comme nous l'avons vu, la dérivée d'une fonction à un point donné nous donne le taux de variation ou la pente de la tangente à la fonction à ce point. Si nous différencions une fonction de position à un moment donné, nous obtenons la vitesse à cet instant. Il semble raisonnable de conclure que connaître la dérivée de la fonction à chaque point produirait des informations précieuses sur le comportement de la fonction. Cependant, le processus consistant à trouver la dérivée ne serait-ce que pour une poignée de valeurs en utilisant les techniques de la section précédente deviendrait rapidement assez fastidieux. Dans cette section, nous définissons la fonction dérivée et apprenons comment la trouver.
Fonctions dérivées
La fonction dérivée donne la dérivée d'une fonction à chaque point du domaine de la fonction d'origine pour laquelle la dérivée est définie. Nous pouvons définir formellement une fonction dérivée comme suit.
\(f\)Soyons une fonction. La fonction dérivée, désignée par\(f'\), est la fonction dont le domaine est constitué des valeurs\(x\) telles que la limite suivante existe :
\[f'(x)=\lim_{h→0}\frac{f(x+h)−f(x)}{h}. \label{derdef} \]
Une fonction\(f(x)\) est dite dérivable\(f'(a)\) lorsqu'\(a\)elle existe. Plus généralement, une fonction est dite dérivable\(S\) si elle est dérivable à chaque point d'un ensemble ouvert\(S\), et une fonction dérivable est une fonction qui\(f'(x)\) existe sur son domaine.
Dans les exemples suivants, nous utilisons l'équation \ ref {derdef} pour trouver la dérivée d'une fonction.
Trouvez la dérivée de\(f(x)=\sqrt{x}\).
Solution
Commencez directement par la définition de la fonction dérivée.
Substituer\(f(x+h)=\sqrt{x+h}\) et\(f(x)=\sqrt{x}\) insérer\(f'(x)= \displaystyle \lim_{h→0}\frac{f(x+h)−f(x)}{h}\).
| \(f'(x)=\displaystyle \lim_{h→0}\frac{\sqrt{x+h}−\sqrt{x}}{h}\) | |
| \(=\displaystyle\lim_{h→0}\frac{\sqrt{x+h}−\sqrt{x}}{h}⋅\frac{\sqrt{x+h}+\sqrt{x}}{\sqrt{x+h}+\sqrt{x}}\) | Multipliez le numérateur et le dénominateur par\(\sqrt{x+h}+\sqrt{x}\) sans les répartir dans le dénominateur. |
| \(=\displaystyle\lim_{h→0}\frac{h}{h\left(\sqrt{x+h}+\sqrt{x}\right)}\) | Multipliez les numérateurs et simplifiez. |
| \(=\displaystyle\lim_{h→0}\frac{1}{\left(\sqrt{x+h}+\sqrt{x}\right)}\) | Annulez le\(h\). |
| \(=\dfrac{1}{2\sqrt{x}}\) | Évaluez la limite |
Trouvez la dérivée de la fonction\(f(x)=x^2−2x\).
Solution
Suivez la même procédure ici, mais sans avoir à multiplier par le conjugué.
Substituer\(f(x+h)=(x+h)^2−2(x+h)\) et\(f(x)=x^2−2x\) introduire\(f'(x)= \displaystyle \lim_{h→0}\frac{f(x+h)−f(x)}{h}.\)
| \(f'(x)=\displaystyle\lim_{h→0}\frac{((x+h)^2−2(x+h))−(x^2−2x)}{h}\) | |
| \(=\displaystyle\lim_{h→0}\frac{x^2+2xh+h^2−2x−2h−x^2+2x}{h}\) | Élargir\((x+h)^2−2(x+h)\). |
| \(=\displaystyle\lim_{h→0}\frac{2xh−2h+h^2}{h}\) | SIMPLIFIER |
| \(=\displaystyle\lim_{h→0}\frac{h(2x−2+h)}{h}\) | Extraire\(h\) du numérateur |
| \(=\displaystyle\lim_{h→0}(2x−2+h)\) | Annulez le facteur commun de\(h\) |
| \(=2x−2\) | Évaluez la limite |
Trouvez le dérivé de\(f(x)=x^2\).
- Allusion
-
Utilisez l'équation \ ref {derdef} et suivez l'exemple.
- Réponse
-
\(f'(x)=2x\)
Nous utilisons différentes notations pour exprimer la dérivée d'une fonction. Dans l'exemple,\(\PageIndex{2}\) nous avons montré que si\(f(x)=x^2−2x\), alors\(f'(x)=2x−2\). Si nous avions exprimé cette fonction sous la forme\(y=x^2−2x\), nous aurions pu exprimer la dérivée sous la forme\(y′=2x−2\) ou\(\dfrac{dy}{dx}=2x−2\). Nous aurions pu transmettre les mêmes informations par écrit\(\dfrac{d}{dx}\left(x^2−2x\right)=2x−2\). Ainsi, pour la fonction\(y=f(x)\), chacune des notations suivantes représente la dérivée de\(f(x)\) :
\(f'(x), \quad \dfrac{dy}{dx}, \quad y′,\quad \dfrac{d}{dx}\big(f(x)\big)\).
À la place de,\(f'(a)\) nous pouvons également utiliser\(\dfrac{dy}{dx}\Big|_{x=a}\). L'utilisation de la\(\dfrac{dy}{dx}\) notation (appelée notation Leibniz) est assez courante en ingénierie et en physique. Pour mieux comprendre cette notation, rappelons que la dérivée d'une fonction en un point est la limite des pentes des droites sécantes lorsque les droites sécantes s'approchent de la tangente. Les pentes de ces raies sécantes sont souvent exprimées sous la forme\(\dfrac{Δy}{Δx}\) où\(Δy\) est la différence entre les\(y\) valeurs correspondant à la différence entre les\(x\) valeurs, qui sont exprimées sous la forme\(Δx\) (Figure\(\PageIndex{1}\)). Ainsi, la dérivée, qui peut être considérée comme le taux de variation instantané de\(y\) par rapport à\(x\), est exprimée comme
\(\displaystyle \frac{dy}{dx}= \lim_{Δx→0}\frac{Δy}{Δx}\).
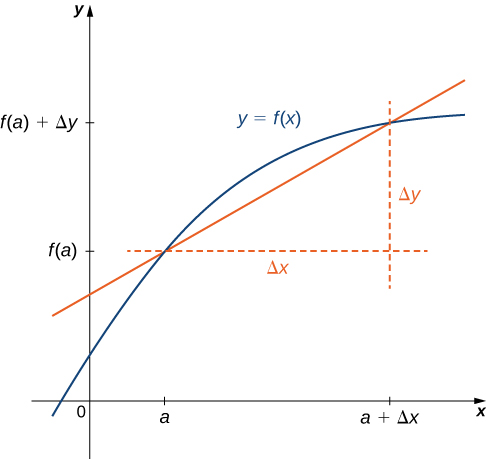
Représentation graphique d'une dérivée
Nous avons déjà discuté de la façon de représenter graphiquement une fonction. Ainsi, à partir de l'équation d'une fonction ou de l'équation d'une fonction dérivée, nous pourrions la représenter graphiquement. Compte tenu des deux, nous pouvons nous attendre à voir une correspondance entre les graphes de ces deux fonctions, car\(f'(x)\) cela donne le taux de variation d'une fonction\(f(x)\) (ou la pente de la tangente à\(f(x)\)).
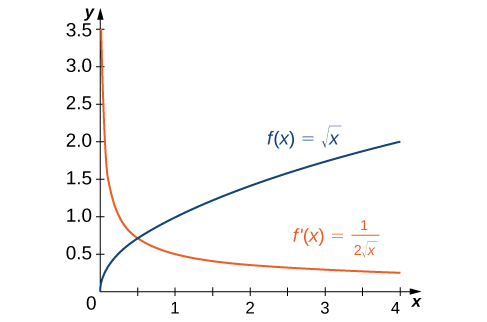
Dans l'exemple,\(\PageIndex{1}\), nous avons constaté que pour\(f(x)=\sqrt{x}\),\(f'(x)=\frac{1}{2\sqrt{x}}\). Si nous représentons ces fonctions sur les mêmes axes, comme dans la Figure\(\PageIndex{2}\), nous pouvons utiliser les graphes pour comprendre la relation entre ces deux fonctions. Tout d'abord, nous remarquons qu'elle\(f(x)\) augmente sur l'ensemble de son domaine, ce qui signifie que les pentes de ses tangentes en tous points sont positives. Par conséquent, nous attendons\(f'(x)>0\) pour toutes les valeurs de x dans son domaine. De plus, à mesure qu'elles\(x\) augmentent, les pentes des lignes\(f(x)\) tangentes à diminuent et nous nous attendons à une diminution correspondante\(f'(x)\). Nous observons également que ce n'\(f(0)\)est pas défini et que cela\(\displaystyle \lim_{x→0^+}f'(x)=+∞\) correspond à une tangente verticale à\(f(x)\) at\(0\).
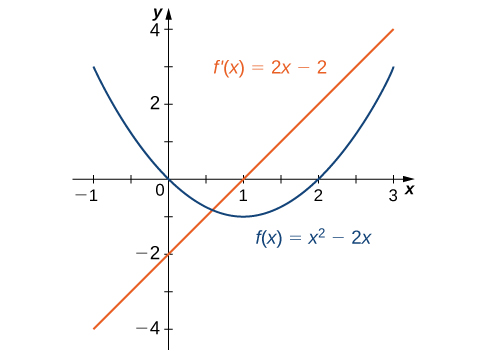
Dans l'exemple\(\PageIndex{2}\), nous avons constaté que pour\(f(x)=x^2−2x,\; f'(x)=2x−2\). Les graphiques de ces fonctions sont présentés dans la figure\(\PageIndex{3}\). Observez que cela\(f(x)\) diminue pour\(x<1\). Pour ces mêmes valeurs de\(x\),\(f'(x)<0\). Pour les valeurs de\(x>1\),\(f(x)\) augmente et\(f'(x)>0\). \(f(x)\)Possède également une tangente horizontale à\(x=1\) et\(f'(1)=0\).
Utilisez le graphique suivant de\(f(x)\) pour esquisser un graphique de\(f'(x)\).
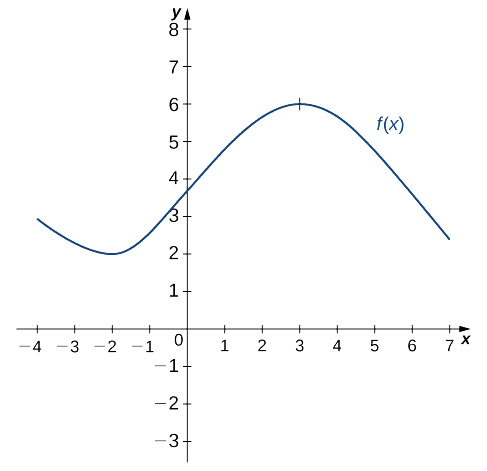
Solution
La solution est illustrée dans le graphique suivant. Observez que cela\(f(x)\) augmente et ainsi de\(f'(x)>0\) suite\((–2,3)\). De plus,\(f(x)\) diminue et\(f'(x)<0\) encore\((−∞,−2)\) et encore\((3,+∞)\). Notez également qu'il\(f(x)\) possède des tangentes horizontales à\(–2\) et\(3\),\(f'(−2)=0\) et\(f'(3)=0\).
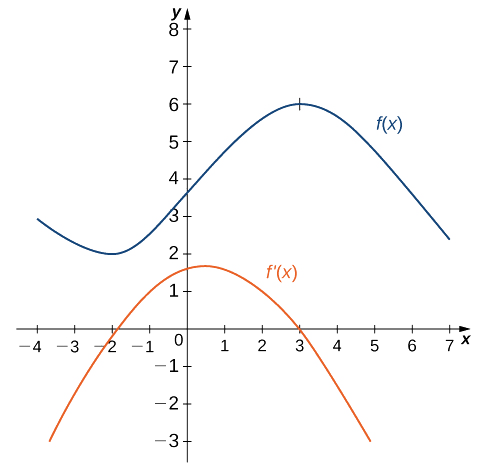
Esquissez le graphique de\(f(x)=x^2−4\). Sur quel intervalle se trouve le graphique\(f'(x)\) au-dessus de l'\(x\)axe Y ?
- Allusion
-
Le graphique de\(f'(x)\) est positif là où\(f(x)\) il augmente.
- Réponse
-
\((0,+∞)\)
Produits dérivés et continuité
Maintenant que nous pouvons représenter graphiquement une dérivée, examinons le comportement des graphes. Tout d'abord, nous examinons la relation entre la différentiabilité et la continuité. Nous verrons que si une fonction est dérivable en un point, elle doit y être continue ; cependant, une fonction continue en un point n'a pas besoin d'être dérivable à ce point. En fait, une fonction peut être continue à un point et ne pas être dérivable à ce point pour plusieurs raisons.
\(f(x)\)Soyons une fonction et\(a\) soyons dans son domaine. Si\(f(x)\) est différenciable à\(a\), alors\(f\) est continu à\(a\).
\(f(x)\)Il est différenciable à\(a\), puis\(f'(a)\) existe et, si nous le laissons faire\(h = x - a\), nous l'avons fait\( x = a + h \)\(h=x-a\to 0\), et comme nous pouvons le voir\(x\to a\).
Alors
\[ f'(a) = \lim_{h\to 0}\frac{f(a+h)-f(a)}{h}\nonumber \]
peut être réécrit comme
\(f'(a)=\displaystyle \lim_{x→a}\frac{f(x)−f(a)}{x−a}\).
Nous voulons montrer que cela\(f(x)\) est continu\(a\) en montrant que\(\displaystyle \lim_{x→a}f(x)=f(a).\) Ainsi,
\ (\ begin {align*} \ displaystyle \ lim_ {x→a} f (x) &= \ lim_ {x→a} \ ; \ big (f (x) −f (a) +f (a) \ grand) \ \ [4 points]
&= \ lim_ {x→a} \ left (\ frac {f (x) −f (a)} {x−a} (⋅ x−a) +f (a) \ right) & \ text {Multipliez et divisez} (f (x) −f (a)) \ text {par} x−a. \ \ [4pt]
&= \ left (\ lim_ {x→a} \ frac {f (x) −f (a)} {x−a} \ right) ⋅ \ gauche (\ lim_ {x→a} \ ; (x−a) \ droite) + \ lim_ {x→a} f (a) \ \ [4 points]
&=f' (a) ⋅0+f (a) \ \ [4 points]
&=f (a). \ end {align*} \)
Par conséquent, puisque\(f(a)\) est défini et\(\displaystyle \lim_{x→a}f(x)=f(a)\), nous concluons que\(f\) c'est continu à\(a\).
□
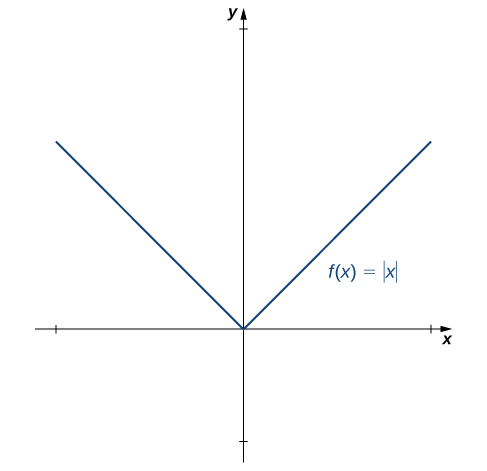
Nous venons de prouver que la différentiabilité implique la continuité, mais nous examinons maintenant si la continuité implique la différentiabilité. Pour trouver une réponse à cette question, nous examinons la fonction\(f(x)=|x|\). Cette fonction est continue partout, mais elle n'\(f'(0)\)est pas définie. Cette observation nous amène à penser que la continuité n'implique pas la différentiabilité. Explorons davantage. Pour\(f(x)=|x|\),
\(f'(0)=\displaystyle \lim_{x→0}\frac{f(x)−f(0)}{x−0}= \lim_{x→0}\frac{|x|−|0|}{x−0}= \lim_{x→0}\frac{|x|}{x}\).
Cette limite n'existe pas parce que
\(\displaystyle \lim_{x→0^−}\frac{|x|}{x}=−1\)et\(\displaystyle \lim_{x→0^+}\frac{|x|}{x}=1\).
Voir la figure\(\PageIndex{4}\).
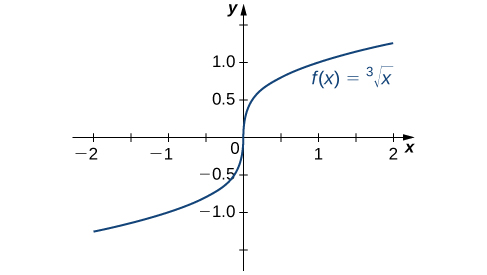
Examinons d'autres situations dans lesquelles une fonction continue ne peut pas être différenciée. Considérez la fonction\(f(x)=\sqrt[3]{x}\) :
\(f'(0)=\displaystyle \lim_{x→0}\frac{\sqrt[3]{x}−0}{x−0}=\displaystyle \lim_{x→0}\frac{1}{\sqrt[3]{x^2}}=+∞\).
Cela\(f'(0)\) n'existe pas. Un rapide coup d'œil au graphique de\(f(x)=\sqrt[3]{x}\) clarifie la situation. La fonction possède une tangente verticale à\(0\) (Figure\(\PageIndex{5}\)).
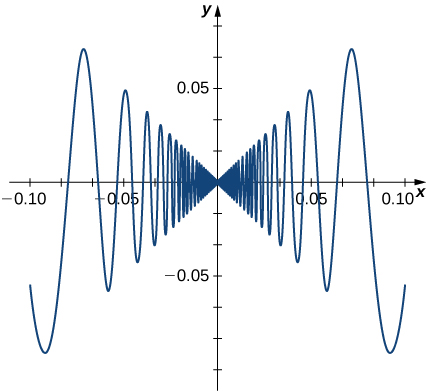
La fonction possède\(f(x)=\begin{cases} x\sin\left(\frac{1}{x}\right), & & \text{ if } x≠0\\0, & & \text{ if } x=0\end{cases}\) également une dérivée qui présente un comportement intéressant à\(0\).
Nous voyons que
\(f'(0)=\displaystyle \lim_{x→0}\frac{x\sin\left(1/x\right)−0}{x−0}= \lim_{x→0}\sin\left(\frac{1}{x}\right)\).
Cette limite n'existe pas, essentiellement parce que les pentes des lignes sécantes changent continuellement de direction lorsqu'elles s'approchent de zéro (Figure\(\PageIndex{6}\)).
En résumé :
- Nous observons que si une fonction n'est pas continue, elle ne peut pas être dérivée, puisque chaque fonction dérivable doit être continue. Toutefois, si une fonction est continue, elle risque de ne pas être dérivable.
- Nous avons constaté que cela\(f(x)=|x|\) n'était pas différenciable à\(0\) parce que les limites des pentes des lignes tangentes à gauche et à droite n'étaient pas les mêmes. Visuellement, cela a donné lieu à un angle net sur le graphique\(0.\) de la fonction à. Nous en concluons que pour être dérivable en un point, une fonction doit être « lisse » à ce point.
- Comme nous l'avons vu dans l'exemple de\(f(x)=\sqrt[3]{x}\), une fonction ne peut pas être dérivée à un point où se trouve une tangente verticale.
- Comme nous l'avons vu,\(f(x)=\begin{cases}x\sin\left(\frac{1}{x}\right), & & \text{ if } x≠0\\0, & &\text{ if } x=0\end{cases}\) une fonction peut également ne pas être différenciable à un moment donné de manière plus compliquée.
Une entreprise de jouets souhaite concevoir une piste pour une petite voiture qui commence le long d'une courbe parabolique puis se transforme en ligne droite (Figure\(\PageIndex{7}\)). La fonction qui décrit la piste est d'avoir la forme\(f(x)=\begin{cases}\frac{1}{10}x^2+bx+c, & & \text{ if }x<−10\\−\frac{1}{4}x+\frac{5}{2}, & & \text{ if } x≥−10\end{cases}\) où\(x\) et\(f(x)\) sont en pouces. Pour que la voiture se déplace en douceur sur la piste, la fonction\(f(x)\) doit être à la fois continue et différenciable à\(−10\). Trouvez des valeurs de\(b\) et\(c\) qui rendent\(f(x)\) à la fois continu et différenciable.
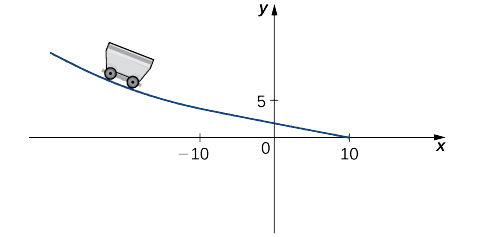
Solution
Pour que la fonction soit continue à\(x=−10\),\(\displaystyle \lim_{x→10^−}f(x)=f(−10)\). Ainsi, puisque
\(\displaystyle \lim_{x→−10^−}f(x)=\frac{1}{10}(−10)^2−10b+c=10−10b+c\)
et\(f(−10)=5\) nous l'avons dû\(10−10b+c=5\). De manière équivalente, nous l'avons fait\(c=10b−5\).
Pour que la fonction soit dérivable à\(−10\),
\(f'(10)=\displaystyle \lim_{x→−10}\frac{f(x)−f(−10)}{x+10}\)
doit exister. Comme elle\(f(x)\) est définie à l'aide de règles différentes à droite et à gauche, nous devons évaluer cette limite à droite et à gauche, puis les mettre égales les unes aux autres :
\ (\ displaystyle \ begin {align*} \ lim_ {x→−10^−} \ frac {f (x) −f (−10)} {x+10} &= \ lim_ {x→−10^−} \ frac {1} {10} x^2+bx+c−5} {x+10} \ \ [4 points]
&= \ lim_ {x→−10^−} \ frac {1} {10} x^2+bx+ (10b−5) −5} {x+10} & & \ text {Substitut} c=10b−5. \ \ [4 points]
&= \ lim_ {x→−10^−} \ frac {x^2−100+10bx+ 100b} {10 (x+10)} \ \ [4pt]
&= \ lim_ {x→−10^−} \ frac {(x+10) (x−10+10b)} {10 (x+10)} & & \ text {Facteur par regroupement} \ \ [4 points]
&=b−2 \ end {align*} \).
Nous avons également
\ (\ displaystyle \ begin {align*} \ lim_ {x→−10^+} \ frac {f (x) −f (−10)} {x+10} &= \ lim_ {x→−10^+} \ frac {− \ frac {1} {4} x+ \ frac {5} {2} −5} {x+10} \ \ [4pt]
&= \ lim_ {x→−10^+} \ frac {− (x+10)} {4 (x+10)} \ \ [4 points]
&=− \ frac {1} {4} \ end {align*} \).
Cela nous donne\(b−2=−\frac{1}{4}\). Ainsi\(b=\frac{7}{4}\) et\(c=10(\frac{7}{4})−5=\frac{25}{2}\).
Trouvez les valeurs de a et de b qui rendent\(f(x)=\begin{cases}ax+b, & & \text{ if } x<3\\x^2, & & \text{ if } x≥3\end{cases}\) à la fois continu et dérivable à\(3\).
- Allusion
-
Utilisez Example\(\PageIndex{4}\) comme guide.
- Réponse
-
\(a=6\)et\(b=−9\)
Produits dérivés d'ordre supérieur
La dérivée d'une fonction est elle-même une fonction, nous pouvons donc trouver la dérivée d'une dérivée. Par exemple, la dérivée d'une fonction de position est le taux de changement de position, ou de vitesse. La dérivée de la vitesse est le taux de variation de la vitesse, qui est l'accélération. La nouvelle fonction obtenue en différenciant la dérivée est appelée dérivée seconde. De plus, nous pouvons continuer à prendre des dérivés pour obtenir la troisième dérivée, la quatrième dérivée, etc. Collectivement, ces produits sont appelés dérivés d'ordre supérieur. La notation pour les dérivées d'ordre supérieur de\(y=f(x)\) peut être exprimée sous l'une des formes suivantes :
\(f''(x),\; f'''(x),\; f^{(4)}(x),\; …\; ,\; f^{(n)}(x)\)
\(y''(x),\; y'''(x),\; y^{(4)}(x),\; …\; ,\; y^{(n)}(x)\)
\(\dfrac{d^2y}{dx^2},\;\dfrac{d^3y}{dy^3},\;\dfrac{d^4y}{dy^4},\;…\;,\;\dfrac{d^ny}{dy^n}.\)
Il est intéressant de noter que la notation pour\(\dfrac{d^2y}{dx^2}\) peut être considérée comme une tentative\(\dfrac{d}{dx}\left(\dfrac{dy}{dx}\right)\) d'expression plus compacte.
De manière analogue,\(\dfrac{d}{dx}\left(\dfrac{d}{dx}\left(\dfrac{dy}{dx}\right)\right)=\dfrac{d}{dx}\left(\dfrac{d^2y}{dx^2}\right)=\dfrac{d^3y}{dx^3}\).
Pour\(f(x)=2x^2−3x+1\), trouvez\(f''(x)\).
Solution
Première découverte\(f'(x)\).
Substituer\(f(x)=2x^2−3x+1\) et\(f(x+h)=2(x+h)^2−3(x+h)+1\) introduire\(f'(x)=\displaystyle \lim_{h→0}\dfrac{f(x+h)−f(x)}{h}.\)
| \(f'(x)=\displaystyle \lim_{h→0}\frac{(2(x+h)^2−3(x+h)+1)−(2x^2−3x+1)}{h}\) | |
| \(=\displaystyle \lim_{h→0}\frac{4xh+2h^2−3h}{h}\) | Simplifiez le numérateur. |
| \(=\displaystyle \lim_{h→0}(4x+2h−3)\) | Facturez le\(h\) dans le numérateur et annulez avec le\(h\) dans le dénominateur. |
| \(=4x−3\) | Prenez la limite. |
Ensuite, trouvez\(f''(x)\) en prenant la dérivée de\(f'(x)=4x−3.\)
| \(f''(x)=\displaystyle \lim_{h→0}\frac{f'(x+h)−f'(x)}{h}\) | Utiliser\(f'(x)=\displaystyle \lim_{h→0}\frac{f(x+h)−f(x)}{h}\) avec\(f ′(x)\) à la place de\(f(x).\) |
| \(=\displaystyle \lim_{h→0}\frac{(4(x+h)−3)−(4x−3)}{h}\) | Substitut\(f'(x+h)=4(x+h)−3\) et\(f'(x)=4x−3.\) |
| \(=\displaystyle \lim_{h→0}4\) | Simplifiez. |
| \(=4\) | Prenez la limite. |
Trouvez\(f''(x)\) pour\(f(x)=x^2\).
- Allusion
-
Nous l'avons trouvé\(f'(x)=2x\) dans un précédent poste de contrôle. Utilisez l'équation \ ref {derdef} pour trouver la dérivée de\(f'(x)\)
- Réponse
-
\(f''(x)=2\)
La position d'une particule le long d'un axe de coordonnées à un moment donné\(t\) (en secondes) est donnée par\(s(t)=3t^2−4t+1\) (en mètres). Trouvez la fonction qui décrit son accélération à la fois\(t\).
Solution
Depuis\(v(t)=s′(t)\) et\(a(t)=v′(t)=s''(t)\), nous commençons par trouver la dérivée de\(s(t)\) :
\ (\ displaystyle \ begin {align*} s′ (t) &= \ lim_ {h→0} \ frac {s (t+h) −s (t)} {h} \ \ [4pt]
&= \ lim_ {h→0} \ frac {3 (t+h) ^2−4 (t+h) +1− (3t^2−4t+1) {} h} \ \ [4 points]
&=6t−4. \ end {align*} \)
Ensuite,
\ (\ displaystyle \ begin {align*} s « (t) &= \ lim_ {h→0} \ frac {s′ (t+h) −s′ (t)} {h} \ \ [4 points]
&= \ lim_ {h→0} \ frac {6 (t+h) −4− (6t−4)} {h} \ \ [4 points]
&=6. \ end {align*} \)
Ainsi,\(a=6 \;\text{m/s}^2\).
Pour\(s(t)=t^3\), trouvez\(a(t).\)
- Allusion
-
Utilisez Example\(\PageIndex{6}\) comme guide.
- Réponse
-
\(a(t)=6t\)
Concepts clés
- La dérivée d'une fonction\(f(x)\) est la fonction dont la valeur at\(x\) est\(f'(x)\).
- Le graphe d'une dérivée d'une fonction\(f(x)\) est lié au graphe de\(f(x)\). Où\(f(x)\) a une tangente à pente positive,\(f'(x)>0\). Où\(f(x)\) a une tangente à pente négative,\(f'(x)<0\). Où\(f(x)\) a une tangente horizontale,\(f'(x)=0.\)
- Si une fonction est dérivable en un point, elle est continue à ce point. Une fonction n'est pas dérivable en un point si elle n'est pas continue au point, si elle possède une tangente verticale au point ou si le graphique présente un angle ou une pointe.
- Les dérivés d'ordre supérieur sont des dérivés de dérivés, de la dérivée seconde à la\(n^{\text{th}}\) dérivée.
Équations clés
- La fonction dérivée
\(f'(x)=\displaystyle \lim_{h→0}\frac{f(x+h)−f(x)}{h}\)
Lexique
- fonction dérivée
- donne la dérivée d'une fonction à chaque point du domaine de la fonction d'origine pour laquelle la dérivée est définie
- différenciable à\(a\)
- une fonction pour laquelle\(f'(a)\) il existe est dérivable à\(a\)
- différenciable sur\(S\)
- une fonction qui\(f'(x)\) existe pour chacun\(x\) dans l'ensemble ouvert\(S\) est dérivable sur\(S\)
- fonction dérivable
- une fonction pour laquelle\(f'(x)\) il existe est une fonction dérivable
- dérivé d'ordre supérieur
- une dérivée d'une dérivée, de la dérivée seconde à la\(n^{\text{th}}\) dérivée, est appelée dérivée d'ordre supérieur
Contributeurs et attributions
- Template:ContribOpenStaxCalc
- Paul Seeburger (Monroe Community College) added explanation of the alternative definition of the derivative used in the proof of that differentiability implies continuity.


