3.1E : Exercices pour la section 3.1
- Page ID
- 197854
Pour les exercices 1 à 10, utilisez l'équation\( m_{\text{sec}}=\dfrac{f(x)−f(a)}{x−a} \) pour déterminer la pente de la droite sécante entre les valeurs\(x_1\) et\(x_2\) pour chaque fonction\(y=f(x)\).
1)\(f(x)=4x+7; \quad x_1=2, \quad x_2=5\)
- Réponse
- \(m_{\text{sec}}=4\)
2)\(f(x)=8x−3;\quad x_1=−1,\quad x_2=3\)
3)\(f(x)=x^2+2x+1;\quad x_1=3,\quad x_2=3.5\)
- Réponse
- \(m_{\text{sec}}=8.5\)
4)\(f(x)=−x^2+x+2;\quad x_1=0.5,\quad x_2=1.5\)
5)\(f(x)=\dfrac{4}{3x−1};\quad x_1=1,\quad x_2=3\)
- Réponse
- \(m_{\text{sec}}=−\frac{3}{4}\)
6)\(f(x)=\dfrac{x−7}{2x+1};\quad x_1=−2,\quad x_2=0\)
7)\(f(x)=\sqrt{x};\quad x_1=1,\quad x_2=16\)
- Réponse
- \(m_{\text{sec}}=0.2\)
8)\(f(x)=\sqrt{x−9};\quad x_1=10,\quad x_2=13\)
9)\(f(x)=x^{1/3}+1;\quad x_1=0,\quad x_2=8\)
- Réponse
- \(m_{\text{sec}}=0.25\)
10)\(f(x)=6x^{2/3}+2x^{1/3};\quad x_1=1,\quad x_2=27\)
Pour les fonctions des exercices 11 à 20,
a. utilisez l'équation\( \displaystyle m_{\text{tan}}=\lim_{h→0}\frac{f(a+h)−f(a)}{h} \) pour déterminer la pente de la tangente\(m_{\text{tan}}=f′(a)\), et
b. trouve l'équation de la tangente à\(f\) at\(x=a\).
11)\(f(x)=3−4x, \quad a=2\)
- Réponse
- a.\(m_{\text{tan}}=−4\)
b.\(y=−4x+3\)
(12)\(f(x)=\dfrac{x}{5}+6, \quad a=−1\)
13)\(f(x)=x^2+x, \quad a=1\)
- Réponse
- a.\(m_{\text{tan}}=3\)
b.\(y=3x−1\)
(14)\(f(x)=1−x−x^2, \quad a=0\)
(15)\(f(x)=\dfrac{7}{x}, \quad a=3\)
- Réponse
- a.\(m_{\text{tan}}=\frac{−7}{9}\)
b.\(y=\frac{−7}{9}x+\frac{14}{3}\)
16)\(f(x)=\sqrt{x+8}, \quad a=1\)
17)\(f(x)=2−3x^2, \quad a=−2\)
- Réponse
- a.\(m_{\text{tan}}=12\)
b.\(y=12x+14\)
18)\(f(x)=\dfrac{−3}{x−1}, \quad a=4\)
19)\(f(x)=\dfrac{2}{x+3}, \quad a=−4\)
- Réponse
- a.\(m_{\text{tan}}=−2\)
b.\(y=−2x−10\)
(20)\(f(x)=\dfrac{3}{x^2}, \quad a=3\)
Pour les fonctions des exercices 21\(y=f(x)\) à 30, déterminez à\(f′(a)\) l'aide de l'équation\( \displaystyle f′(a)=\lim_{x→a}\frac{f(x)−f(a)}{x−a} \).
(21)\(f(x)=5x+4, \quad a=−1\)
- Réponse
- \(f'(-1) = 5\)
(22)\(f(x)=−7x+1, \quad a=3\)
23)\(f(x)=x^2+9x, \quad a=2\)
- Réponse
- \(f'(2) = 13\)
(24)\(f(x)=3x^2−x+2, \quad a=1\)
25)\(f(x)=\sqrt{x}, \quad a=4\)
- Réponse
- \(f'(4) = \frac{1}{4}\)
(26)\(f(x)=\sqrt{x−2}, \quad a=6\)
(27)\(f(x)=\dfrac{1}{x}, \quad a=2\)
- Réponse
- \(f'(2) = −\frac{1}{4}\)
(28)\(f(x)=\dfrac{1}{x−3}, \quad a=−1\)
(29)\(f(x)=\dfrac{1}{x^3}, \quad a=1\)
- Réponse
- \(f'(1) = -3\)
(30)\(f(x)=\dfrac{1}{\sqrt{x}}, \quad a=4\)
Pour les exercices suivants, compte tenu de la fonction\(y=f(x)\),
a. Trouvez la pente de la droite sécante\(PQ\) pour chaque point\(Q(x,f(x))\) avec\(x\) la valeur indiquée dans le tableau.
b. Utilisez les réponses de a. pour estimer la valeur de la pente de la tangente à\(P\).
c. Utilisez la réponse de b. pour trouver l'équation de la tangente\(f\) au point\(P\).
31) [T]\(f(x)=x^2+3x+4, \quad P(1,8)\) (Arrondir à la\(6\) décimale.)
| \(x\) | \(Slope m_{PQ}\) | \(x\) | \(Slope m_{PQ}\) |
| 1.1 | (i) | 0,9 | (vii) |
| 1,01 | (ii) | 0,99 | (viii) |
| 1,001 | (iii) | 0,999 | (ix) |
| 1 001 | (iv) | 0,9999 | (x) |
| 1 00001 | (v) | 0,99999 | (xi) |
| 1 000 001 | (vi) | 0,999999 | (xii) |
- Réponse
- \(a. (i)5.100000, (ii)5.010000, (iii)5.001000, (iv)5.000100, (v)5.000010, (vi)5.000001, (vii)4.900000, (viii)4.990000, (ix)4.999000, (x)4.999900, (xi)4.999990, (x)4.999999\)
b.\(m_{\text{tan}}=5\)
c.\(y=5x+3\)
32) [T]\(f(x)=\dfrac{x+1}{x^2−1}, \quad P(0,−1)\)
| \(x\) | \(Slope m_{PQ}\) | \(x\) | \(Slope m_{PQ}\) |
| 0,1 | (i) | −0,1 | (vii) |
| 0,01 | (ii) | −0,01 | (viii) |
| 0,001 | (iii) | −0,001 | (ix) |
| 0,0001 | (iv) | −0,0001 | (x) |
| 0,00001 | (v) | −0,00001 | (xi) |
| 0,000001 | (vi) | −0,000001 | (xii) |
33) [T]\(f(x)=10e^{0.5x}, \quad P(0,10)\) (Arrondir à la\(4\) décimale.)
| \(x\) | \(Slope m_{PQ}\) |
| −0,1 | (i) |
| −0,01 | (ii) |
| −0,001 | (iii) |
| −0,0001 | (iv) |
| −0,00001 | (v) |
| −0,000001 | (vi) |
- Réponse
- a.\((i)4.8771, \;(ii)4.9875, \;(iii)4.9988, \;(iv)4.9999, \;(v)4.9999, \;(vi)4.9999 \)
b.\(m_{\text{tan}}=5\)
c.\(y=5x+10\)
34) [T]\(f(x)=\tan(x), \quad P(π,0)\)
| \(x\) | \(Slope m_{PQ}\) |
| 3.1 | (i) |
| 3.14 | (ii) |
| 3.141 | (iii) |
| 3.1415 | (iv) |
| 3.14159 | (v) |
| 3.141592 | (vi) |
[T] Pour les fonctions de position suivantes\(y=s(t)\), un objet se déplace le long d'une ligne droite, en secondes et\(s\) en mètres.\(t\) Trouvez
a. l'expression simplifiée de la vitesse moyenne de\(t=2\) à\(t=2+h\) ;
b. la vitesse moyenne entre\(t=2\) et\(t=2+h\)\((i)\;h=0.1, \;(ii)\;h=0.01, \;(iii)\;h=0.001\), où et\((iv)\;h=0.0001\) ; et
c. utilisez la réponse de a. pour estimer la vitesse instantanée à la\(t=2\) seconde.
35)\(s(t)=\frac{1}{3}t+5\)
- Réponse
- a.\(\frac{1}{3}\) ;
b.\((i)\;\frac{1}{3}\) m/s,\((ii)\;\frac{1}{3}\) m/s,\((iii)\;\frac{1}{3}\) m/s,\((iv)\;\frac{1}{3}\) m/s ;
c.\(\frac{1}{3}\) m/s
36)\(s(t)=t^2−2t\)
(37)\(s(t)=2t^3+3\)
- Réponse
- a.\(2(h^2+6h+12)\) ;
b.\((i)\;25.22\) m/s,\((ii)\; 24.12\) m/s,\((iii)\; 24.01\) m/s,\((iv)\; 24\) m/s ;
c.\(24\) m/s
38)\(s(t)=\dfrac{16}{t^2}−\dfrac{4}{t}\)
39) Utilisez le graphique suivant pour évaluer a.\(f′(1)\) et b.\(f′(6).\)
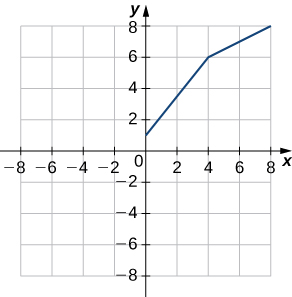
- Réponse
- a.\(1.25\) ; b.\(0.5\)
40) Utilisez le graphique suivant pour évaluer a.\(f′(−3)\) et\(f′(1.5)\) b.
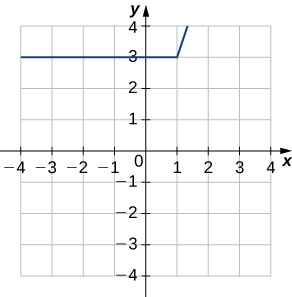
Pour les exercices suivants, utilisez la définition limite de la dérivée pour montrer que la dérivée n'existe pas\(x=a\) pour chacune des fonctions données.
41)\(f(x)=x^{1/3}, \quad x=0\)
- Réponse
- \(\displaystyle \lim_{x→0^−}\frac{x^{1/3}−0}{x−0}=\lim_{x→0^−}\frac{1}{x^{2/3}}=∞\)
(42)\(f(x)=x^{2/3}, \quad x=0\)
43)\(f(x)=\begin{cases}1, & \text{if } x<1\\x, & \text{if } x≥1\end{cases}, \quad x=1\)
- Réponse
- \(\displaystyle \lim_{x→1^−}\frac{1−1}{x−1}=0≠1=\lim_{x→1^+}\frac{x−1}{x−1}\)
44)\(f(x)=\dfrac{|x|}{x}, \quad x=0\)
45) [T] La position en pieds d'une voiture de course sur une piste droite après\(t\) quelques secondes est modélisée par la fonction\(s(t)=8t^2−\frac{1}{16}t^3.\)
a. Déterminez la vitesse moyenne du véhicule sur les intervalles de temps suivants, à quatre décimales près :
i. [\(4, 4.1\)]
ii. [\(4, 4.01\)]
iii. [\(4, 4.001\)]
iv. [\(4, 4.0001\)]
b. Utilisez a. pour tirer une conclusion sur la vitesse instantanée du véhicule en\(t=4\) secondes.
- Réponse
- a.\((i)61.7244 ft/s, \;(ii)61.0725 ft/s, \;(iii)61.0072 ft/s, \;(iv)61.0007 ft/s\)
b. En\(4\) quelques secondes, la voiture de course roule à une cadence/vitesse de\(61\) pieds/s.
46) [T] La distance en pieds sur laquelle une balle roule le long d'une pente est modélisée par la fonction\(s(t)=14t^2\),
où t survient quelques secondes après que la balle commence à rouler.
a. Déterminez la vitesse moyenne de la balle sur les intervalles de temps suivants :
i. [5, 5.1]
ii. [5, 5.01]
iii. [5, 5.001]
iv. [5, 50001]
b. Utilisez les réponses de a. pour tirer une conclusion sur la vitesse instantanée de la balle en\(t=5\) secondes.
47) Deux véhicules partent côte à côte sur une route droite. Leurs fonctions de position, illustrées dans le graphique suivant, sont données par\(s=f(t)\) et\(s=g(t)\), où s est mesuré en pieds et t est mesuré en secondes.
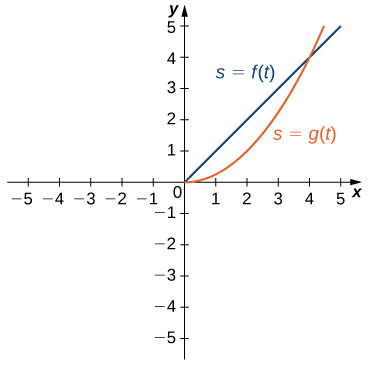
a. Quel véhicule s'est déplacé le plus loin en\(t=2\) quelques secondes ?
b. Quelle est la vitesse approximative de chaque véhicule en\(t=3\) secondes ?
c. Quel véhicule se déplace plus vite en\(t=4\) quelques secondes ?
d. Qu'est-ce qui est vrai en ce qui concerne la position des véhicules en\(t=4\) quelques secondes ?
- Réponse
- a. Le véhicule représenté par\(f(t)\), parce qu'il a parcouru des\(2\) pieds, alors qu'il\(g(t)\) a parcouru\(1\) du pied.
b. La vitesse de\(f(t)\) est constante à\(1\) pieds/s, tandis que la vitesse de\(g(t)\) est d'environ\(2\) pieds/s.
c. Le véhicule représenté par\(g(t)\), avec une vitesse d'environ\(4\) pieds/s.
d. Les deux ont parcouru \(4\)pieds en\(4\) quelques secondes.
48) [T] Le coût total\(C(x)\), en centaines de dollars, de la production de\(x\) pots de mayonnaise est donné par\(C(x)=0.000003x^3+4x+300\).
a. Calculez le coût moyen par pot sur les intervalles suivants :
i. [100, 100,1]
ii. [100, 100,01]
iii. [100, 100 001]
iv. [100, 100 0001]
b. Utilisez les réponses du point a. pour estimer le coût moyen de production de\(100\) pots de mayonnaise.
49) [T] Pour la fonction\(f(x)=x^3−2x^2−11x+12\), procédez comme suit.
a. Utilisez une calculatrice graphique\(f\) pour représenter graphiquement une fenêtre de visualisation appropriée.
b. Utilisez la fonction ZOOM de la calculatrice pour obtenir une approximation des deux valeurs\(x=a\) pour lesquelles\(m_{tan}=f′(a)=0\).
- Réponse
-
un.
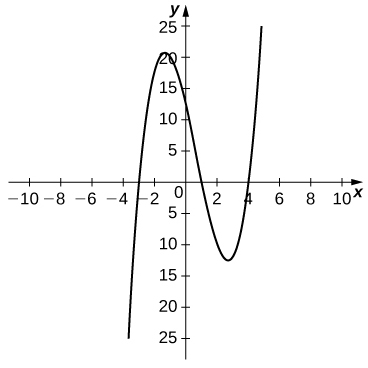
b.\(a≈−1.361,\;2.694\)
50) [T] Pour la fonction\(f(x)=\dfrac{x}{1+x^2}\), procédez comme suit.
a. Utilisez une calculatrice graphique\(f\) pour représenter graphiquement une fenêtre de visualisation appropriée.
b. Utilisez la fonction ZOOM de la calculatrice pour obtenir une approximation des valeurs\(x=a\) pour lesquelles\(m_{\text{tan}}=f′(a)=0\).
51) Supposons que cela\(N(x)\) calcule le nombre de gallons d'essence utilisés par un véhicule parcourant des\(x\) kilomètres. Supposons que le véhicule atteigne le\(30\) mpg.
a. Trouvez une expression mathématique pour\(N(x)\).
b. Qu'est-ce que c'est\(N(100)\) ? Expliquez la signification physique.
c. Qu'est-ce que c'est\(N′(100)\) ? Expliquez la signification physique.
- Réponse
- a.\(N(x)=\dfrac{x}{30}\)
b. ∼\(3.3\) gallons. Lorsque le véhicule parcourt des\(100\) kilomètres, il a consommé des\(3.3\) gallons d'essence.
\(\frac{1}{30}\)c. Taux de consommation d'essence en gallons par mile que le véhicule atteint après avoir parcouru des\(100\) kilomètres.
52) [T] Pour la fonction\(f(x)=x^4−5x^2+4\), procédez comme suit.
a. Utilisez une calculatrice graphique\(f\) pour représenter graphiquement une fenêtre de visualisation appropriée.
b. Utilisez la\(nDeriv\) fonction, qui trouve numériquement la dérivée, sur une calculatrice graphique pour estimer\(f′(−2),\;f′(−0.5),\;f′(1.7)\), et\(f′(2.718)\).
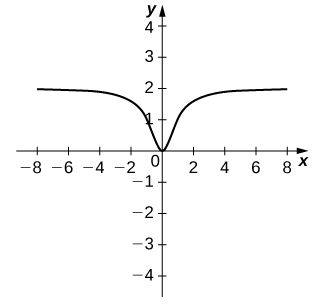
53) [T] Pour la fonction\(f(x)=\dfrac{x^2}{x^2+1}\), procédez comme suit.
a. Utilisez une calculatrice graphique\(f\) pour représenter graphiquement une fenêtre de visualisation appropriée.
b. Utilisez la\(nDeriv\) fonction d'une calculatrice graphique pour trouver\(f′(−4),\;f′(−2),\;f′(2)\), et\(f′(4)\).
- Réponse
-
un.
b.\(−0.028,−0.16,0.16,0.028\)

