Skip to main content
Global

9.7 : Racines supérieures

  1. Last updated
  2. Save as PDF
  • Page ID
    194536

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Objectifs d'apprentissage

    À la fin de cette section, vous serez en mesure de :

    • Simplifiez les expressions avec des racines
    • Utilisez la propriété Product pour simplifier les expressions ayant des racines supérieures
    • Utilisez la propriété Quotient pour simplifier les expressions ayant des racines plus élevées
    • Ajouter et soustraire des racines supérieures
    Remarque
    1. Simplifiez :\(y^{5}y^{4}\).
      Si vous avez oublié ce problème, consultez l'exemple 6.2.7.
    2. Simplifiez :\((n^2)^6\).
      Si vous avez oublié ce problème, consultez l'exemple 6.2.19.
    3. Simplifiez :\(\frac{x^8}{x^3}\).
      Si vous avez oublié ce problème, consultez l'exemple 6.5.1.

    Simplifiez les expressions avec des racines

    Jusqu'à présent, dans ce chapitre, nous avons travaillé avec des carrés et des racines carrées. Nous allons maintenant étendre notre travail pour inclure des puissances supérieures et des racines plus élevées.

    Passons d'abord en revue un peu de vocabulaire.

    \[\begin{array}{cc} {}&{}\\ {\textbf{We write:}}&{\textbf{We say:}}\\ {n^2}&{\text{n squared}}\\ {n^3}&{\text{n cubed}}\\ {n^4}&{\text{n to the fourth}}\\ {n^5}&{\text{n to the fifth}}\\ \nonumber \end{array}\]

    Les termes « carré » et « cube » proviennent des formules de l'aire d'un carré et du volume d'un cube.

    Il sera utile de disposer d'un tableau des puissances des nombres entiers compris entre −5 et 5. Voir la figure\(\PageIdnex{1}\).

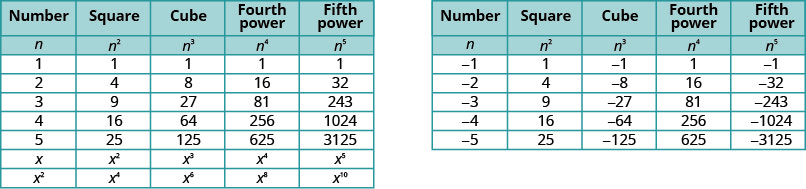
    Cette figure se compose de deux tableaux. Le premier tableau montre les résultats de l'augmentation des nombres 1, 2, 3, 4, 5, x et x au carré aux deuxième, troisième, quatrième et cinquième puissances. Le deuxième tableau montre les résultats de l'augmentation des nombres de moins un à moins cinq vers les deuxième, troisième, quatrième et cinquième puissances. Le tableau comporte d'abord cinq colonnes et neuf lignes. La seconde comporte cinq colonnes et sept rangées. Les colonnes des deux tableaux sont intitulées « Numéro », « Carré », « Cube », « Quatrième puissance », « Cinquième puissance », rien, « Numéro », « Carré », « Cube », « Quatrième puissance » et « Cinquième puissance ». Dans les deux tableaux, la rangée suivante se lit comme suit : n, n au carré, n au cube, n à la quatrième puissance, n à la cinquième puissance, rien, n, n au carré, n au cube, n à la quatrième puissance et n à la cinquième puissance. Dans le premier tableau, 1 puissance au carré, 1 puissance au cube, 1 à la quatrième puissance et 1 à la cinquième puissance sont toutes indiquées comme étant égales à 1. Dans la rangée suivante, 2 au carré correspond à 4, 2 au cube correspond à 8, 2 à la quatrième puissance vaut 16 et 2 à la cinquième puissance est 32. Dans la rangée suivante, 3 au carré correspond à 9, 3 au cube correspond à 27, 3 à la quatrième puissance est 81 et 3 à la cinquième puissance est 243. Dans la rangée suivante, 4 au carré correspond à 16, 4 au cube correspond à 64, 4 à la quatrième puissance est 246 et 4 à la cinquième puissance est 1024. Dans la rangée suivante, 5 au carré correspond à 25, 5 au cube correspond à 125, 5 à la quatrième puissance est 625 et 5 à la cinquième puissance est 3125. Dans la rangée suivante, x au carré, x au cube, x à la quatrième puissance et x à la cinquième puissance sont listés. Dans la rangée suivante, x au carré représente x à la quatrième puissance, x au cube au carré est x à la cinquième puissance, x au carré à la quatrième puissance est x à la huitième puissance, et x au carré à la cinquième puissance est x à la dixième puissance. Dans le deuxième tableau, moins 1 au carré vaut 1, moins 1 au cube est négatif 1, moins 1 à la quatrième puissance vaut 1, et moins 1 à la cinquième puissance est négatif 1. Dans la rangée suivante, moins 2 au carré vaut 4, moins 2 au cube est moins 8, moins 2 à la quatrième puissance est 16 et moins 2 à la cinquième puissance est négative 32. Dans la rangée suivante, moins 4 au carré vaut 16, moins 4 au cube correspond à moins 64, moins 4 à la quatrième puissance est 256 et moins 4 à la cinquième puissance est négative 1024. Dans la rangée suivante, moins 5 au carré vaut 25, moins 5 au cube est moins 125, moins 5 à la quatrième puissance est 625 et moins 5 à la cinquième puissance est négative 3125.
    Figure\(\PageIndex{1}\) : De la première à la cinquième puissance des nombres entiers compris entre −5 et 5.

    Remarquez les signes sur la figure\(\PageIndex{1}\). Toutes les puissances des nombres positifs sont positives, bien entendu. Mais lorsque nous avons un nombre négatif, les puissances paires sont positives et les puissances impaires sont négatives. Nous allons copier la ligne avec les puissances de −2 ci-dessous pour vous aider à le voir.

    Cette figure comporte cinq colonnes et deux rangées. La première ligne indique chaque colonne : n, n au carré, n au cube, n à la quatrième puissance et n à la cinquième puissance. La deuxième ligne se lit comme suit : moins 2, 4, moins 8, 16 et moins 32.

    Plus tôt dans ce chapitre, nous avons défini la racine carrée d'un nombre.

    Si\(n^2=m\), alors n est la racine carrée de m.

    Et nous avons utilisé la notation\(\sqrt{m}\) pour désigner la racine carrée principale. Donc,\(\sqrt{m} \ge 0\) toujours.

    Nous allons maintenant étendre la définition aux racines supérieures.

    Définition : À LA RACINE D'UN NOMBRE

    Si\(b^n=a\), alors b est un à la racine d'un nombre a.

    Le principal à la racine de a est écrit\(\sqrt[n]{a}=b\)

    n est appelé indice du radical.

    Nous n'écrivons pas l'index pour une racine carrée. Tout comme nous utilisons le mot « cube » pour\(b^3\), nous utilisons le terme « racine cubique » pour\(\sqrt[3]{a}\).

    Nous nous référons à la Figure\(\PageIndex{1}\) pour nous aider à trouver des racines plus élevées.

    \[\begin{array}{cc} {4^3=64}&{\sqrt[3]{64}=4}\\ {3^4=81}&{\sqrt[4]{81}=3}\\ {(−2)^5=−32}&{\sqrt[5]{−32}=−2}\\ \nonumber \end{array}\]

    Pourrions-nous avoir une racine paire d'un nombre négatif ? Non. Nous savons que la racine carrée d'un nombre négatif n'est pas un nombre réel. Il en va de même pour toute racine paire. Même les racines de nombres négatifs ne sont pas des nombres réels. Les racines impaires des nombres négatifs sont des nombres réels.

    Définition : PROPRIÉTÉS DE\(\sqrt[n]{a}\)

    Lorsque n est un nombre pair et

    • \(a\ge 0\), alors\(\sqrt[n]{a}\) est un nombre réel
    • \(a < 0\), alors n'\(\sqrt[n]{a}\)est pas un nombre réel

    Lorsque n est un nombre impair,\(\sqrt[n]{a}\) est un nombre réel pour toutes les valeurs de a.

    Exemple\(\PageIndex{1}\)

    Simplifiez :

    1. \(\sqrt[3]{8}\)
    2. \(\sqrt[4]{81}\)
    3. \(\sqrt[5]{32}\).
    Réponse
    1. \(\sqrt[3]{8}\)
    Depuis\((2)^3=8\). 2
    2. \(\sqrt[4]{81}\)
    Depuis\((3)^4=81\). 3
    3. \(\sqrt[5]{32}\)
    Depuis\((2)^5=32\). 2
    Exemple\(\PageIndex{2}\)

    Simplifiez :

    1. \(\sqrt[3]{27}\)
    2. \(\sqrt[4]{256}\)
    3. \(\sqrt[5]{243}\).
    Réponse
    1. 3
    2. 4
    3. 3
    Exemple\(\PageIndex{3}\)

    Simplifiez :

    1. \(\sqrt[3]{1000}\)
    2. \(\sqrt[4]{16}\)
    3. \(\sqrt[5]{32}\).
    Réponse
    1. 10
    2. 2
    3. 2
    Exemple\(\PageIndex{4}\)

    Simplifiez :

    1. \(\sqrt[3]{−64}\)
    2. \(\sqrt[4]{−16}\)
    3. \(\sqrt[5]{−243}\).
    Réponse
    1. \(\sqrt[3]{−64}\)
    Depuis\((−4)^3=−64\). −4
    2. \(\sqrt[4]{−16}\)
    \((?)^4=−16\)Réfléchis, aucun chiffre réel porté à la quatrième puissance n'est positif. Ce n'est pas un vrai chiffre.
    3. \(\sqrt[5]{−243}\)
    Depuis\((−3)^5=−243\). −3
    Exemple\(\PageIndex{5}\)

    Simplifiez :

    1. \(\sqrt[3]{−125}\)
    2. \(\sqrt[4]{−16}\)
    3. \(\sqrt[5]{−32}\).
    Réponse
    1. −5
    2. pas réel
    3. −2
    Exemple\(\PageIndex{6}\)

    Simplifiez :

    1. \(\sqrt[3]{−216}\)
    2. \(\sqrt[4]{−81}\)
    3. \(\sqrt[5]{−1024}\).
    Réponse
    1. −6
    2. pas réel
    3. −4
    Lorsque nous avons travaillé avec des racines carrées contenant des variables dans le radicand, nous avons limité les variables à des valeurs non négatives. Nous allons maintenant supprimer cette restriction.

    La racine impaire d'un nombre peut être positive ou négative. Nous l'avons vu\(\sqrt[3]{−64}=−4\).

    Mais la racine paire d'un nombre non négatif est toujours non négative, car nous prenons le principal à la racine.

    Supposons que nous commencions par a=−5.

    \[\begin{array}{cc} {(−5)^4=625}&{\sqrt[4]{625}=5}\\ \nonumber \end{array}\]

    Comment pouvons-nous nous assurer que la racine 4 de −5 portée à la quatrième puissance\((−5)^4\) est 5 ? Nous verrons dans la propriété suivante.

    Définition : SIMPLIFIER LES RACINES PAIRES ET IMPAIRES

    Pour n'importe quel entier\(n \ge 2\),

    \[\begin{array}{cc} {\text{when n is odd}}&{\sqrt[n]{a^n}=a}\\ {\text{when n is even}}&{\sqrt[n]{a^n}=|a|}\\ \nonumber \end{array}\]

    Nous devons utiliser les signes de valeur absolue lorsque nous prenons la racine paire d'une expression avec une variable dans le radical.

    Exemple\(\PageIndex{7}\)

    Simplifiez :

    1. \(\sqrt{x^2}\)
    2. \(\sqrt[3]{n^3}\)
    3. \(\sqrt[4]{p^4}\)
    4. \(\sqrt[5]{y^5}\).
    Réponse

    Nous utilisons la valeur absolue pour être sûrs d'obtenir la racine positive.

    1. \(\sqrt{x^2}\)
    Depuis\((x)^2=x^2\), et nous voulons une racine positive. |x|
    2. \(\sqrt[3]{n^3}\)
    Depuis\((n)^3=n^3\). C'est une racine étrange, donc aucun signe de valeur absolue n'est nécessaire. n
    3. \(\sqrt[4]{p^4}\)
    Depuis\((p)^4=p^4\), et nous voulons une racine positive. |p|
    4. \(\sqrt[5]{y^5}\)
    Depuis\((y)^5=y^5\). C'est une racine étrange, donc aucun signe de valeur absolue n'est nécessaire. y
    Exemple\(\PageIndex{8}\)

    Simplifiez :

    1. \(\sqrt{b^2}\)
    2. \(\sqrt[3]{w^3}\)
    3. \(\sqrt[4]{m^4}\)
    4. \(\sqrt[5]{q^5}\).
    Réponse
    1. |b|
    2. w
    3. |m|
    4. q
    Exemple\(\PageIndex{9}\)

    Simplifiez :

    1. \(\sqrt{y^2}\)
    2. \(\sqrt[3]{p^3}\)
    3. \(\sqrt[4]{z^4}\)
    4. \(\sqrt[5]{q^5}\)
    Réponse
    1. |a|
    2. p
    3. |z|
    4. q
    Exemple\(\PageIndex{10}\)

    Simplifiez :

    1. \(\sqrt[3]{y^{18}}\)
    2. \(\sqrt[4]{z^8}\).
    Réponse
    1. \(\sqrt[3]{y^{18}}\)
    Depuis\((y^6)^3=y^18\). \(\sqrt[3]{(y^6)^3}\)
      \(y^6\)
    2. \(\sqrt[4]{z^8}\)
    Depuis\((z^2)^4=z^8\). \(\sqrt[4]{(z^2)^4}\)
    Comme\(z^2\) c'est positif, nous n'avons pas besoin d'un signe de valeur absolue. \(z^2\)
    Exemple\(\PageIndex{11}\)

    Simplifiez :

    1. \(\sqrt[4]{u^{12}}\)
    2. \(\sqrt[3]{v^{15}}\).
    Réponse
    1. \(u^3\)
    2. \(v^5\)
    Exemple\(\PageIndex{12}\)

    Simplifiez :

    1. \(\sqrt[5]{c^{20}}\)
    2. \(\sqrt[6]{d^{24}}\).
    Réponse
    1. \(c^4\)
    2. \(d^4\)
    Exemple\(\PageIndex{13}\)

    Simplifiez :

    1. \(\sqrt[3]{64p^6}\)
    2. \(\sqrt[4]{16q^{12}}\).
    Réponse
    1. \(\sqrt[3]{64p^6}\)
    Réécrivez\(64p^6\) en tant que\((4p^2)^3\). \(\sqrt[3]{(4p^2)^3}\)
    Prenez la racine cubique. \(4p^2\)
    2. \(\sqrt[4]{16q^{12}}\)
    Réécrivez le radicand en tant que quatrième puissance. \(\sqrt[4]{(2q^3)^4}\)
    Prenez la quatrième racine. \(2|q^3|\)
    Exemple\(\PageIndex{14}\)

    Simplifiez :

    1. \(\sqrt[3]{27x^{27}}\)
    2. \(\sqrt[4]{81q^{28}}\).
    Réponse
    1. \(3x^9\)
    2. \(3∣q^7∣\)
    Exemple\(\PageIndex{15}\)

    Simplifiez :

    1. \(\sqrt[3]{125p^9}\)
    2. \(\sqrt[5]{243q^{25}}\)
    Réponse
    1. \(5p^3\)
    2. \(3q^5\)

    Utilisez la propriété Product pour simplifier les expressions ayant des racines plus élevées

    Nous simplifierons les expressions avec des racines supérieures de la même manière que nous avons simplifié les expressions avec des racines carrées. Et la racine est considérée comme simplifiée si elle ne comporte aucun facteur de\(m^n\).

    Définition : SIMPLIFIÉ À LA RACINE

    \(\sqrt[n]{a}\)est considéré comme simplifié si a ne comporte aucun facteur de\(m^n\).

    Nous allons généraliser la propriété de produit des racines carrées pour inclure n'importe quelle racine entière\(n \ge 2\).

    Définition : PROPRIÉTÉ DU PRODUIT DE N TH ROOTS

    \(\sqrt[n]{ab}=\sqrt[n]{a}·\sqrt[n]{b}\)et\(\sqrt[n]{a}·\sqrt[n]{b}=\sqrt[n]{ab}\)

    quand\(\sqrt[n]{a}\) et\(\sqrt[n]{b}\) sont des nombres réels et pour n'importe quel entier\(n \ge 2\)

    Exemple\(\PageIndex{16}\)

    Simplifiez :

    1. \(\sqrt[3]{x^4}\)
    2. \(\sqrt[4]{x^7}\).
    Réponse

    1.

    		 \(\sqrt[3]{x^4}\)
    Réécrivez le radicand en tant que produit en utilisant le plus grand facteur cube parfait. \(\sqrt[3]{x^3·x}\)
    Réécrivez le radical comme étant le produit de deux radicaux. \(\sqrt[3]{x^3}·\sqrt[3]{x}\)
    Simplifiez. \(x\sqrt[3]{x}\)
    2. \(\sqrt[4]{x^7}\)
    Réécrivez le radicand en tant que produit en utilisant le quatrième facteur de puissance parfait le plus élevé. \(\sqrt[4]{x^4·x^3}\)
    Réécrivez le radical comme étant le produit de deux radicaux. \(\sqrt[4]{x^4}·\sqrt[4]{x^3}\)
    Simplifiez. \(|x|\sqrt[4]{x^3}\)
    Exemple\(\PageIndex{17}\)

    Simplifiez :

    1. \(\sqrt[4]{y^6}\)
    2. \(\sqrt[3]{z^5}\).
    Réponse
    1. \(|y∣\sqrt[4]{y^2}\)
    2. \(z\sqrt[3]{z^2}\)
    Exemple\(\PageIndex{18}\)

    Simplifiez :

    1. \(\sqrt[5]{p^8}\)
    2. \(\sqrt[6]{q^{13}}\).
    Réponse
    1. \(p\sqrt[5]{p^3}\)
    2. \( q^2\sqrt[6]{q}\)
    Exemple\(\PageIndex{19}\)

    Simplifiez :

    1. \(\sqrt[3]{16}\)
    2. \(\sqrt[4]{243}\).
    Réponse
    1. \(\sqrt[3]{16}\)
      \(\sqrt[3]{2^4}\)
    Réécrivez le radicand en tant que produit en utilisant le plus grand facteur cube parfait. \(\sqrt[3]{2^3·2}\)
    Réécrivez le radical comme étant le produit de deux radicaux. \(\sqrt[3]{2^3}·\sqrt[3]{2}\)
    Simplifiez. \(2\sqrt[3]{2}\)
    2. \(\sqrt[4]{243}\)
      \(\sqrt[4]{3^5}\)
    Réécrivez le radicand en tant que produit en utilisant le quatrième facteur de puissance parfait le plus élevé. \(\sqrt[4]{3^4·3}\)
    Réécrivez le radical comme étant le produit de deux radicaux. \(\sqrt[4]{3^4}·\sqrt[4]{3}\)
    Simplifiez. \(3\sqrt[4]{3}\)
    Exemple\(\PageIndex{20}\)

    Simplifiez :

    1. \(\sqrt[3]{81}\)
    2. \(\sqrt[4]{64}\).
    Réponse
    1. \(3\sqrt[3]{3}\)
    2. \(2\sqrt[4]{4}\)
    Exemple\(\PageIndex{21}\)

    Simplifiez :

    1. \(\sqrt[3]{625}\)
    2. \(\sqrt[4]{729}\).
    Réponse
    1. \(5\sqrt[3]{5}\)
    2. \(3\sqrt[4]{9}\)

    N'oubliez pas d'utiliser les signes de valeur absolue lorsque vous prenez la racine paire d'une expression avec une variable dans le radical.

    Exemple\(\PageIndex{22}\)

    Simplifiez :

    1. \(\sqrt[3]{24x^7}\)
    2. \(\sqrt[4]{80y^{14}}\).
    Réponse
    1. \(\sqrt[3]{24x^7}\)
    Réécrivez le radicand en tant que produit en utilisant des facteurs cubiques parfaits. \(\sqrt[3]{2^{3}x^{6}·3x}\)
    Réécrivez le radical comme étant le produit de deux radicaux. \(\sqrt[3]{2^{3}x^{6}}·\sqrt[3]{3x}\)
    Réécrivez le premier radicand comme\((2x^2)^3\) \(\sqrt[3]{(2x^{2})^3}·\sqrt[3]{3x}\)
    Simplifiez. \(2x^2\sqrt[3]{3x}\)
    2. \(\sqrt[4]{80y^{14}}\)
    Réécrivez le radicand en tant que produit en utilisant un quatrième facteur de puissance parfait. \(\sqrt[4]{2^{4}y^{12}·5y^2}\)
    Réécrivez le radical comme étant le produit de deux radicaux. \(\sqrt[4]{2^{4}y^{12}}·\sqrt[4]{5y^2}\)
    Réécrivez le premier radicand comme\((2y^3)^4\) \(\sqrt[4]{(2y^3)^4}·\sqrt[4]{5y^2}\)
    Simplifiez. \(2|y^3|\sqrt[4]{5y^2}\)
    Exemple\(\PageIndex{23}\)

    Simplifiez :

    1. \(\sqrt[3]{54p^[10}]\)
    2. \(\sqrt[4]{64q^{10}}\).
    Réponse
    1. \(3p^3\sqrt[3]{2p}\)
    2. \(2q^2\sqrt[4]{4q^2}\)
    Exemple\(\PageIndex{24}\)

    Simplifiez :

    1. \(\sqrt[3]{128m^{11}}\)
    2. \(\sqrt[4]{162n^7}\).
    Réponse
    1. \(4m^3\sqrt[3]{2m^2}\)
    2. \(3|n|\sqrt[4]{2n^3}\)
    Exemple\(\PageIndex{25}\)

    Simplifiez :

    1. \(\sqrt[3]{−27}\)
    2. \(\sqrt[4]{−16}\).
    Réponse
    1. \(\sqrt[3]{−27}\)
    Réécrivez le radicand en tant que produit en utilisant des facteurs cubiques parfaits. \(\sqrt[3]{(−3)^3}\)
    Prenez la racine cubique. −3
    2. \(\sqrt[4]{−16}\)
    Il n'y a pas de chiffre réel où\(n^4=−16\). Ce n'est pas un vrai chiffre.
    Exemple\(\PageIndex{26}\)

    Simplifiez :

    1. \(\sqrt[3]{−108}\)
    2. \(\sqrt[4]{−48}\).
    Réponse
    1. \(−3\sqrt[3]{4}\)
    2. pas réel
    Exemple\(\PageIndex{27}\)

    Simplifiez :

    1. \(\sqrt[3]{−625}\)
    2. \(\sqrt[4]{−324}\).
    Réponse
    1. \(−5\sqrt[3]{5}\)
    2. pas réel

    Utilisez la propriété Quotient pour simplifier les expressions ayant des racines plus élevées

    Nous pouvons simplifier les racines supérieures avec des quotients de la même manière que nous avons simplifié les racines carrées. On simplifie d'abord toutes les fractions à l'intérieur du radical.

    Exemple\(\PageIndex{28}\)

    Simplifiez :

    1. \(\sqrt[3]{\frac{a^8}{a^5}}\)
    2. \(\sqrt[4]{\frac{a^{10}}{a^2}}\).
    Réponse

    1.

    		 \(\sqrt[3]{\frac{a^8}{a^5}}\)
    Simplifiez d'abord la fraction sous le radical. \(\sqrt[3]{a^3}\)
    Simplifiez. un
    2. \(\sqrt[4]{\frac{a^{10}}{a^2}}\)
    Simplifiez d'abord la fraction sous le radical. \(\sqrt[4]{a^8}\)
    Réécrivez le radicand en utilisant un quatrième facteur de puissance parfait. \(\sqrt[4]{(a^2)^4}\)
    Simplifiez. \(a^2\)
    Exemple\(\PageIndex{29}\)

    Simplifiez :

    1. \(\sqrt[4]{\frac{x^7}{x^3}}\)
    2. \(\sqrt[4]{\frac{y^{17}}{y^5}}\).
    Réponse
    1. |x|
    2. \(y^3\)
    Exemple\(\PageIndex{30}\)

    Simplifiez :

    1. \(\sqrt[3]{\frac{m^{13}}{m^7}}\)
    2. \(\sqrt[5]{\frac{n^{12}}{n^2}}\).
    Réponse
    1. \(m^2\)
    2. \(n^2\)

    Auparavant, nous utilisions la propriété du quotient « à l'envers » pour simplifier les racines carrées. Nous allons maintenant généraliser la formule pour inclure les racines supérieures.

    Définition : PROPRIÉTÉ DU QUOTIENT DES RACINES

    \(\sqrt[n]{\frac{a}{b}}=\frac{\sqrt[n]{a}}{\sqrt[n]{b}}\)et\(\frac{\sqrt[n]{a}}{\sqrt[n]{b}}=\sqrt[n]{\frac{a}{b}}\)

    quand\(\sqrt[n]{a}\) and \(\sqrt[n]{b}\) are real numbers, \(b \ne 0\), and for any integer \(n \ge 2\)

    Exercice\(\PageIndex{31}\)

    Simplifiez :

    1. \(\frac{\sqrt[3]{−108}}{\sqrt[3]{2}}\)
    2. \(\frac{\sqrt[4]{96x^7}}{\sqrt[4]{3x^2}}\)
    Réponse
    1. \(\frac{\sqrt[3]{−108}}{\sqrt[3]{2}}\)
    Aucun des radicaux n'est un cube parfait. Utilisez donc la propriété Quotient pour écrire comme un radical. \(\sqrt[3]{\frac{−108}{2}}\)
    Simplifiez la fraction sous le radical. \(\sqrt[3]{−54}\)
    Réécrivez le radicand en tant que produit en utilisant des facteurs cubiques parfaits. \(\sqrt[3]{(−3)^3·2}\)
    Réécrivez le radical comme étant le produit de deux radicaux. \(\sqrt[3]{(−3)^3}·\sqrt[3]{2}\)
    Simplifiez. \(−3\sqrt[3]{2}\)
    2. \(\frac{\sqrt[4]{96x^7}}{\sqrt[4]{3x^2}}\)
    Aucun des radicaux n'est un quatrième pouvoir parfait, donc utilisez la propriété Quotient pour écrire comme un radical \(\sqrt[4]{\frac{96x^7}{3x^2}}\)
    Simplifiez la fraction sous le radical. \(\sqrt[4]{32x^5}\)
    Réécrivez le radicand en tant que produit en utilisant un quatrième facteur de puissance parfait. \(\sqrt[4]{2^{4}x^4·2x}\)
    Réécrivez le radical comme étant le produit de deux radicaux. \(\sqrt[4]{(2x)^4}·\sqrt[4]{2x}\)
    Simplifiez. \(2|x|\sqrt[4]{2x}\)
    Exemple\(\PageIndex{32}\)

    Simplifiez :

    1. \(\frac{\sqrt[3]{−532}}{\sqrt[3]{2}}\)
    2. \(\frac{\sqrt[4]{486m^{11}}}{\sqrt[4]{3m^5}}\)
    Réponse
    1. pas réel
    2. \(3|m|\sqrt[4]{2m^2}\)
    Exemple\(\PageIndex{33}\)

    Simplifiez :

    1. \(\frac{\sqrt[3]{−192}}{\sqrt[3]{3}}\)
    2. \(\frac{\sqrt[4]{324n^7}}{\sqrt[4]{2n^3}}\).
    Réponse
    1. −4
    2. \(3|n|\sqrt[4]{2}\)

    Si la fraction à l'intérieur du radical ne peut pas être simplifiée, nous utilisons la première forme de la propriété du quotient pour réécrire l'expression sous la forme du quotient de deux radicaux.

    Exemple\(\PageIndex{34}\)

    Simplifiez :

    1. \(\sqrt[3]{\frac{24x^7}{y^3}}\)
    2. \(\sqrt[4]{\frac{48x^{10}}{y^8}}\).
    Réponse
    1. \(\sqrt[3]{\frac{24x^7}{y^3}}\)
    La fraction du radicand ne peut pas être simplifiée. Utilisez la propriété Quotient pour écrire sous la forme de deux radicaux. \(\frac{\sqrt[3]{24x^7}}{\sqrt[3]{y^3}}\)
    Réécrivez chaque radical en tant que produit en utilisant des facteurs cubiques parfaits. \(\frac{\sqrt[3]{8x^6·3x}}{\sqrt[3]{y^3}}\)
    Réécrivez le numérateur comme étant le produit de deux radicaux. \(\frac{\sqrt[3]{(2x^2)^3}·\sqrt[3]{3x}}{\sqrt[3]{y^3}}\)
    Simplifiez. \(\frac{2x^2\sqrt[3]{3x}}{y}\)
    2. \(\sqrt[4]{\frac{48x^{10}}{y^8}}\)
    La fraction du radicand ne peut pas être simplifiée. Utilisez la propriété Quotient pour écrire sous la forme de deux radicaux. \(\frac{\sqrt[4]{48x^{10}}}{\sqrt[4]{y^8}}\)
    Réécrivez chaque radical en tant que produit en utilisant des facteurs cubiques parfaits. \(\frac{\sqrt[4]{16x^8·3x^2}}{\sqrt[4]{y^8}}\)
    Réécrivez le numérateur comme étant le produit de deux radicaux. \(\frac{\sqrt[4]{(2x^2)^4}·\sqrt[4]{3x^2}}{\sqrt[4]{(y^2)^4}}\)
    Simplifiez. \(\frac{2x^2\sqrt[4]{3x^2}}{y^2}\)
    Exemple\(\PageIndex{35}\)

    Simplifiez :

    1. \(\sqrt[3]{\frac{108c^{10}}{d^6}}\)
    2. \(\sqrt[4]{\frac{80x^{10}}{y^5}}\).
    Réponse
    1. \(\frac{3c^3\sqrt[3]{4c}}{d^2}\)
    2. \(\frac{x^2}{∣y∣}\sqrt[4]{\frac{80x^2}{y}}\)
    Exemple\(\PageIndex{36}\)

    Simplifiez :

    1. \(\sqrt[3]{\frac{40r^3}{s}}\)
    2. \(\sqrt[4]{\frac{162m^{14}}{n^{12}}}\)
    Réponse
    1. \(r\sqrt[3]{\frac{40}{s}}\)
    2. \(\frac{3m^3\sqrt[4]{2m^2}}{∣n^3∣}\)

    Ajouter et soustraire des racines supérieures

    Nous pouvons ajouter et soustraire des racines supérieures comme nous avons ajouté et soustrait des racines carrées. Nous donnons d'abord une définition formelle des radicaux similaires.

    Définition : COMME DES RADICAUX

    Les radicaux ayant le même indice et le même radical sont appelés radicaux similaires.

    Les radicaux similaires ont le même indice et le même radical.

    • \(9\sqrt[4]{42x}\)et\(−2\sqrt[4]{42x}\) sont comme des radicaux.
    • \(5\sqrt[3]{125x}\)et ne\(6\sqrt[3]{125y}\) sont pas comme les radicaux. Les radicands sont différents.
    • \(2\sqrt[5]{1000q}\)et ne\(−4\sqrt[4]{1000q}\) sont pas comme les radicaux. Les indices sont différents.

    Nous ajoutons et soustrayons comme des radicaux de la même manière que nous ajoutons et soustrayons des termes similaires. Nous pouvons ajouter\(9\sqrt[4]{42x}+(−2\sqrt[4]{42x})\) et le résultat est\(7\sqrt[4]{42x}\).

    Exemple\(\PageIndex{37}\)

    Simplifiez :

    1. \(\sqrt[3]{4x}+\sqrt[3]{4x}\)
    2. \(4\sqrt[4]{8}−2\sqrt[4]{8}\)
    Réponse
    1. \(\sqrt[3]{4x}+\sqrt[3]{4x}\)
    Les radicaux sont comme, donc on ajoute les coefficients \(2\sqrt[3]{4x}\)
    2. \(4\sqrt[4]{8}−2\sqrt[4]{8}\)
    Les radicaux sont similaires, donc on soustrait les coefficients. \(2\sqrt[4]{8}\)
    Exemple\(\PageIndex{38}\)

    Simplifiez :

    1. \(\sqrt[5]{3x}+\sqrt[5]{3x}\)
    2. \(3\sqrt[3]{9}−\sqrt[3]{9}\)
    Réponse
    1. \(2\sqrt[5]{3x}\)
    2. \(2\sqrt[3]{9}\)
    Exemple\(\PageIndex{39}\)

    Simplifiez :

    1. \(\sqrt[4]{10y}+\sqrt[4]{10y}\)
    2. \(5\sqrt[6]{32}−3\sqrt[6]{32}\).
    Réponse
    1. \(2\sqrt[4]{10y}\)
    2. \(2\sqrt[6]{32}\)

    Lorsqu'une expression ne semble pas avoir des radicaux similaires, nous allons d'abord simplifier chaque radical. Parfois, cela conduit à une expression avec des radicaux similaires.

    Exemple\(\PageIndex{40}\)

    Simplifiez :

    1. \(\sqrt[3]{54}−\sqrt[3]{16}\)
    2. \(\sqrt[4]{48}+\sqrt[4]{243}\).
    Réponse
    1. \(\sqrt[3]{54}−\sqrt[3]{16}\)
    Réécrivez chaque radical en utilisant des facteurs cubiques parfaits. \(\sqrt[3]{27}·\sqrt[3]{2}−\sqrt[3]{8}·\sqrt[3]{2}\)
    Réécrivez les cubes parfaits. \(\sqrt[3]{(3)^3}·\sqrt[3]{2}−\sqrt[3]{(2)^3}·\sqrt[3]{2}\)
    Simplifiez les radicaux lorsque cela est possible. \(3\sqrt[3]{2}−2\sqrt[3]{2}\)
    Combinez comme des radicaux. \(\sqrt[3]{2}\)
    2. \(\sqrt[4]{48}+\sqrt[4]{243}\)
    Réécrivez en utilisant un quatrième facteur de puissance parfait. \(\sqrt[4]{16}·\sqrt[4]{3}+\sqrt[4]{81}·\sqrt[4]{3}\)
    Réécrivez chaque radical en tant que produit en utilisant des facteurs cubiques parfaits. \(\sqrt[4]{(2)^4}·\sqrt[4]{3}+\sqrt[4]{(3)^4}·\sqrt[4]{3}\)
    Réécrivez le numérateur comme étant le produit de deux radicaux. \(2\sqrt[4]{3}+3\sqrt[4]{3}\)
    Simplifiez. \(5\sqrt[4]{3}\)
    Exemple\(\PageIndex{41}\)

    Simplifiez :

    1. \(\sqrt[3]{192}−\sqrt[3]{81}\)
    2. \(\sqrt[4]{32}+\sqrt[4]{512}\).
    Réponse
    1. \(\sqrt[3]{3}\)
    2. \(6\sqrt[4]{2}\)
    Exemple\(\PageIndex{42}\)

    Simplifiez :

    1. \(\sqrt[3]{108}−\sqrt[3]{250}\)
    2. \(\sqrt[5]{64}+\sqrt[5]{486}\).
    Réponse
    1. \(−\sqrt[3]{2}\)
    2. \(5\sqrt[5]{2}\)
    Exemple\(\PageIndex{43}\)

    Simplifiez :

    1. \(\sqrt[3]{24x^4}−\sqrt[3]{−81x^7}\)
    2. \(\sqrt[4]{162y^9}+\sqrt[4]{512y^5}\).
    Réponse
    1. \(\sqrt[3]{24x^4}−\sqrt[3]{−81x^7}\)
    Réécrivez chaque radical en utilisant des facteurs cubiques parfaits. \(\sqrt[3]{8x^3}·\sqrt[3]{3x}−\sqrt[3]{−27x^6}·\sqrt[3]{3x}\)
    Réécrivez les cubes parfaits. \(\sqrt[3]{(2x)^3}·\sqrt[3]{3x}−\sqrt[3]{(−3x^2)^3}·\sqrt[3]{3x}\)
    Simplifiez les radicaux lorsque cela est possible. \(2x\sqrt[3]{3x}−(−3x^2\sqrt[3]{3x})\)
    2. \(\sqrt[4]{162y^9}+\sqrt[4]{516y^5}\)
    Réécrivez en utilisant un quatrième facteur de puissance parfait. \(\sqrt[4]{81y^8}·\sqrt[4]{2y}+\sqrt[4]{256y^4}·\sqrt[4]{2y}\)
    Réécrivez chaque radical en tant que produit en utilisant des facteurs cubiques parfaits. \(\sqrt[4]{(3y^2)^4}·\sqrt[4]{2y}+\sqrt[4]{(4y)^4}·\sqrt[4]{2y}\)
    Réécrivez le numérateur comme étant le produit de deux radicaux. \(3y^2\sqrt[4]{2y}+4|y|\sqrt[4]{2y}\)
    Exemple\(\PageIndex{44}\)

    Simplifiez :

    1. \(\sqrt[3]{32y^5}−\sqrt[3]{−108y^8}\)
    2. \(\sqrt[4]{243r^{11}}+\sqrt[4]{768r^{10}}\).
    Réponse
    1. \(2y\sqrt[3]{4y^2}+3y^2\sqrt[3]{4y^2}\)
    2. \(3r^2\sqrt[4]{3r^3}+4r^2\sqrt[4]{3r^2}\)
    Exemple\(\PageIndex{45}\)

    Simplifiez :

    1. \(\sqrt[3]{40z^7}−\sqrt[3]{−135z^4}\)
    2. \(\sqrt[4]{80s^{13}}+\sqrt[4]{1280s^6}\).
    Réponse
    1. \(2z^2\sqrt[3]{5z}+3z^5\sqrt[3]{5z}\)
    2. \(2∣s^3∣\sqrt[4]{5s}+4|s|\sqrt[4]{5s}\)
    Accédez à ces ressources en ligne pour obtenir des instructions et des exercices supplémentaires en simplifiant les racines supérieures.
    • Simplifier les racines
    • Ajouter/soustraire des racines avec des indices plus élevés

    Concepts clés

    • Propriétés de
    • \(\sqrt[n]{a}\)lorsque n est un nombre pair et
      • \(a \ge 0\), alors\(\sqrt[n]{a}\) est un nombre réel
      • \(a < 0\), alors n'\(\sqrt[n]{a}\)est pas un nombre réel
      • Lorsque n est un nombre impair,\(\sqrt[n]{a}\) est un nombre réel pour toutes les valeurs de a.
      • Pour tout entier\(n \ge 2\), lorsque n est impair\(\sqrt[n]{a^n}=a\)
      • Pour tout entier\(n \ge 2\), lorsque n est pair\(\sqrt[n]{a^n}=|a|\)
    • \(\sqrt[n]{a}\)est considéré comme simplifié si a ne comporte aucun facteur de\(m^n\).
    • \(\sqrt[n]{ab}=\sqrt[n]{a}·\sqrt[n]{b}\)et\(\sqrt[n]{a}·\sqrt[n]{b}=\sqrt[n]{ab}\)
    • \(\sqrt[n]{\frac{a}{b}}=\frac{\sqrt[n]{a}}{\sqrt[n]{b}}\)et\(\frac{\sqrt[n]{a}}{\sqrt[n]{b}}=\sqrt[n]{\frac{a}{b}}\)
    • Pour combiner des radicaux similaires, il suffit d'ajouter ou de soustraire les coefficients tout en conservant le même radical.

    Lexique

    À la racine d'un nombre
    Si\(b^n=a\), alors b est un à la racine de a.
    principal à la racine
    Le principal à la racine de a est écrit\(\sqrt[n]{a}\).
    indice
    \(\sqrt[n]{a}\)n est appelé indice du radical.
    comme des radicaux
    Les radicaux ayant le même indice et le même radical sont appelés radicaux similaires.