Skip to main content
Global

9.7E : Exercices

  1. Last updated
  2. Save as PDF
  • Page ID
    194548

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    La pratique permet de perfectionner

    Simplifiez les expressions avec des racines

    Dans les exercices suivants, simplifiez.

    Exemple\(\PageIndex{46}\)
    1. \(\sqrt[3]{216}\)
    2. \(\sqrt[4]{256}\)
    3. \(\sqrt[5]{32}\)
    Exemple\(\PageIndex{47}\)
    1. \(\sqrt[3]{27}\)
    2. \(\sqrt[4]{16}\)
    3. \(\sqrt[5]{243}\)
    Réponse
    1. 3
    2. 2
    3. 3
    Exemple\(\PageIndex{48}\)
    1. \(\sqrt[3]{512}\)
    2. \(\sqrt[4]{81}\)
    3. \(\sqrt[5]{1}\)
    Exemple\(\PageIndex{49}\)
    1. \(\sqrt[5]{125}\)
    2. \(\sqrt[4]{1296}\)
    3. \(\sqrt[5]{1024}\)
    Réponse
    1. 5
    2. 6
    3. 4
    Exemple\(\PageIndex{50}\)
    1. \(\sqrt[3]{−8}\)
    2. \(\sqrt[4]{−81}\)
    3. \(\sqrt[5]{−32}\)
    Exemple\(\PageIndex{51}\)
    1. \(\sqrt[3]{−64}\)
    2. \(\sqrt[4]{−16}\)
    3. \(\sqrt[5]{−243}\)
    Réponse
    1. −4
    2. pas réel
    3. −3
    Exemple\(\PageIndex{52}\)
    1. \(\sqrt[3]{−125}\)
    2. \(\sqrt[4]{−1296}\)
    3. \(\sqrt[5]{−1024}\)
    Exemple\(\PageIndex{53}\)
    1. \(\sqrt[3]{−512}\)
    2. \(\sqrt[4]{−81}\)
    3. \(\sqrt[5]{−1}\)
    Réponse
    1. −8
    2. ce n'est pas un vrai chiffre
    3. −1
    Exemple\(\PageIndex{54}\)
    1. \(\sqrt[5]{u^5}\)
    2. \(\sqrt[8]{v^8}\)
    Exemple\(\PageIndex{55}\)
    1. \(\sqrt[3]{a^3}\)

    .

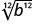
    Réponse
    1. un
    2. |b|
    Exemple\(\PageIndex{56}\)
    1. \(\sqrt[4]{y^4}\)
    2. \(\sqrt[7]{m^7}\)
    Exemple\(\PageIndex{57}\)
    1. \(\sqrt[8]{k^8}\)
    2. \(\sqrt[6]{p^6}\)
    Réponse
    1. |k|
    2. p
    Exemple\(\PageIndex{58}\)
    1. \(\sqrt[3]{x^9}\)
    2. \(\sqrt[4]{y^{12}}\)
    Exemple\(\PageIndex{59}\)
    1. \(\sqrt[5]{a^{10}}\)
    2. \(\sqrt[3]{b^{27}}\)
    Réponse
    1. \(a^2\)
    2. \(b^9\)
    Exemple\(\PageIndex{60}\)
    1. \(\sqrt[4]{m^8}\)
    2. \(\sqrt[5]{n^{20}}\)
    Exemple\(\PageIndex{61}\)
    1. \(\sqrt[6]{r^{12}}\)
    2. \(\sqrt[3]{s^{30}}\)
    Réponse
    1. \(r^2\)
    2. \(s^{10}\)
    Exemple\(\PageIndex{62}\)
    1. \(\sqrt[4]{16x^8}\)
    2. \(\sqrt[6]{64y^{12}}\)
    Exemple\(\PageIndex{63}\)
    1. \(\sqrt[3]{−8c^9}\)
    2. \(\sqrt[3]{125d^{15}}\)
    Réponse
    1. \(−2c^3\)
    2. \(5d^5\)
    Exemple\(\PageIndex{64}\)
    1. \(\sqrt[3]{216a^6}\)
    2. \(\sqrt[5]{32b^{20}}\)
    Exemple\(\PageIndex{65}\)
    1. \(\sqrt[7]{128r^{14}}\)
    2. \(\sqrt[4]{81s^{24}}\)
    Réponse
    1. \(2r^2\)
    2. \(3s^6\)

    Utilisez la propriété Product pour simplifier les expressions ayant des racines plus élevées

    Dans les exercices suivants, simplifiez.

    Exercice\(\PageIndex{66}\)
    1. \(\sqrt[3]{r^5}\)
    2. \(\sqrt[4]{s^{10}}\)
    Exemple\(\PageIndex{67}\)
    1. \(\sqrt[5]{u^7}\)
    2. \(\sqrt[6]{v^{11}}\)
    Réponse
    1. \(u\sqrt[5]{u^2}\)
    2. \(v\sqrt[6]{v^5}\)
    Exemple\(\PageIndex{68}\)
    1. \(\sqrt[4]{m^5}\)
    2. \(\sqrt[8]{n^{10}}\)
    Exemple\(\PageIndex{69}\)
    1. \(\sqrt[5]{p^8}\)
    2. \(\sqrt[3]{q^8}\)
    Réponse
    1. \(p\sqrt[5]{p^3}\)
    2. \(q^2\sqrt[3]{q^2}\)
    Exemple\(\PageIndex{70}\)
    1. \(\sqrt[4]{32}\)
    2. \(\sqrt[5]{64}\)
    Exemple\(\PageIndex{71}\)
    1. \(\sqrt[3]{625}\)
    2. \(\sqrt[6]{128}\)
    Réponse
    1. \(5\sqrt[3]{5}\)
    2. \(2\sqrt[6]{2}\)
    Exemple\(\PageIndex{72}\)
    1. \(\sqrt[6]{64}\)
    2. \(\sqrt[3]{256}\)
    Exemple\(\PageIndex{73}\)
    1. \(\sqrt[4]{3125}\)
    2. \(\sqrt[3]{81}\)
    Réponse
    1. \(5\sqrt[4]{5}\)
    2. \(3\sqrt[3]{3}\)
    Exemple\(\PageIndex{74}\)
    1. \(\sqrt[3]{108x^5}\)
    2. \(\sqrt[4]{48y^6}\)
    Exemple\(\PageIndex{75}\)
    1. \(\sqrt[5]{96a^7}\)
    2. \(\sqrt[3]{375b^4}\)
    Réponse
    1. \(2a\sqrt[5]{3a^2}\)
    2. \(5b\sqrt[3]{3b}\)
    Exemple\(\PageIndex{76}\)
    1. \(\sqrt[4]{405m^{10}}\)
    2. \(\sqrt[5]{160n^8}\)
    Exemple\(\PageIndex{77}\)
    1. \(\sqrt[3]{512p^5}\)
    2. \(\sqrt[4]{324q^7}\)
    Réponse
    1. \(8p\sqrt[3]{p^2}\)
    2. \(3q\sqrt[4]{4q^3}\)
    Exemple\(\PageIndex{78}\)
    1. \(\sqrt[3]{−864}\)
    2. \(\sqrt[4]{−256}\)
    Exemple\(\PageIndex{79}\)
    1. \(\sqrt[5]{−486}\)
    2. \(\sqrt[6]{−64}\)
    Réponse
    1. \(−3\sqrt[5]{2}\)
    2. pas réel
    Exemple\(\PageIndex{80}\)
    1. \(\sqrt[5]{−32}\)
    2. \(\sqrt[8]{−1}\)
    Exemple\(\PageIndex{81}\)
    1. \(\sqrt[3]{−8}\)
    2. \(\sqrt[4]{−16}\)
    Réponse
    1. −2
    2. pas réel
    Utilisez la propriété Quotient pour simplifier les expressions ayant des racines plus élevées

    Dans les exercices suivants, simplifiez.

    Exemple\(\PageIndex{82}\)
    1. \(\sqrt[3]{\frac{p^{11}}{p^2}}\)
    2. \(\sqrt[4]{\frac{q^{17}}{q^{13}}}\)
    Exemple\(\PageIndex{83}\)
    1. \(\sqrt[5]{\frac{d^{12}}{d^7}}\)
    2. \(\sqrt[8]{\frac{m^{12}}{m^4}}\)
    Réponse
    1. d
    2. |m|
    Exemple\(\PageIndex{84}\)
    1. \(\sqrt[5]{\frac{u^{21}}{u^{11}}}\)
    2. \(\sqrt[6]{\frac{v^{30}}{v^{12}}}\)
    Exemple\(\PageIndex{85}\)
    1. \(\sqrt[3]{\frac{r^{14}}{r^5}}\)
    2. \(\sqrt[4]{\frac{c^{21}}{c^9}}\)
    Réponse
    1. \(r^2\)
    2. \(∣c^3∣\)
    Exemple\(\PageIndex{86}\)
    1. \(\frac{\sqrt[4]{64}}{\sqrt[4]{2}}\)
    2. \(\frac{\sqrt[5]{128x^8}}{\sqrt[5]{2x^2}}\)
    Exemple\(\PageIndex{87}\)
    1. \(\frac{\sqrt[3]{−625}}{\sqrt[3]{5}}\)
    2. \(\frac{\sqrt[4]{80m^7}}{\sqrt[4]{5m}}\)
    Réponse
    1. −5
    2. \(4m\sqrt[4]{m^2}\)
    Exemple\(\PageIndex{88}\)
    1. \(\sqrt[3]{\frac{1050}{2}}\)
    2. \(\sqrt[4]{\frac{486y^9}{2y^3}}\)
    Exemple\(\PageIndex{89}\)
    1. \(\sqrt[3]{\frac{162}{6}}\)
    2. \(\sqrt[4]{\frac{160r^{10}}{5r^3}}\)
    Réponse
    1. \(3\sqrt[3]{6}\)
    2. \(2|r|\sqrt[4]{2r^3}\)
    Exemple\(\PageIndex{90}\)
    1. \(\sqrt[3]{\frac{54a^8}{b^3}}\)
    2. \(\sqrt[4]{\frac{64c^5}{d^2}}\)
    Exemple\(\PageIndex{91}\)
    1. \(\sqrt[5]{\frac{96r^{11}}{s^{3}}}\)
    2. \(\sqrt[6]{\frac{128u^7}{v^3}}\)
    Réponse
    1. \(\frac{2r^2\sqrt[5]{3r}}{s^3}\)
    2. \(\frac{2u\sqrt[6]{2uv^3}}{v}\)
    Exemple\(\PageIndex{92}\)
    1. \(\sqrt[3]{\frac{81s^8}{t^3}}\)
    2. \(\sqrt[4]{\frac{64p^{15}}{q^{12}}}\)
    Exemple\(\PageIndex{93}\)
    1. \(\sqrt[3]{\frac{625u^{10}}{v^3}}\)
    2. \(\sqrt[4]{\frac{729c^{21}}{d^8}}\)
    Réponse
    1. \(\frac{5u^3\sqrt[3]{5u}}{v}\)
    2. \(\frac{3c^5\sqrt[4]{9c}}{d^2}\)
    Ajouter et soustraire des racines supérieures

    Dans les exercices suivants, simplifiez.

    Exemple\(\PageIndex{94}\)
    1. \(\sqrt[7]{8p}+\sqrt[7]{8p}\)
    2. \(3\sqrt[3]{25}−\sqrt[3]{25}\)
    Exemple\(\PageIndex{95}\)
    1. \(\sqrt[3]{15q}+\sqrt[3]{15q}\)
    2. \(2\sqrt[4]{27}−6\sqrt[4]{27}\)
    Réponse
    1. \(2\sqrt[3]{15q}\)
    2. \(−4\sqrt[4]{27}\)
    Exemple\(\PageIndex{96}\)
    1. \(3\sqrt[5]{9x}+7\sqrt[5]{9x}\)
    2. \(8\sqrt[7]{3q}−2\sqrt[7]{3q}\)
    Exemple\(\PageIndex{97}\)

    1.

    .

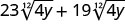
    2.

    .

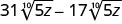
    Réponse

    1.

    .

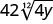
    2.

    .

    Exemple\(\PageIndex{98}\)
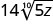
    1. \(\sqrt[3]{81}−\sqrt[3]{192}\)
    2. \(\sqrt[4]{512}−\sqrt[4]{32}\)
    Exemple\(\PageIndex{99}\)
    1. \(\sqrt[3]{250}−\sqrt[3]{54}\)
    2. \(\sqrt[4]{243}−\sqrt[4]{1875}\)
    Réponse
    1. \(5\sqrt[3]{5}−3\sqrt[3]{2}\)
    2. \(−2\sqrt[4]{3}\)
    Exemple\(\PageIndex{100}\)
    1. \(\sqrt[3]{128}+\sqrt[3]{250}\)
    2. \(\sqrt[5]{729}+\sqrt[5]{96}\)
    Exemple\(\PageIndex{101}\)
    1. \(\sqrt[4]{243}+\sqrt[4]{1250}\)
    2. \(\sqrt[3]{2000}+\sqrt[3]{54}\)
    Réponse
    1. \(3\sqrt[4]{3}+5\sqrt[4]{2}\)
    2. \(13\sqrt[3]{2}\)
    Exemple\(\PageIndex{102}\)
    1. \(\sqrt[3]{64a^{10}}−\sqrt[3]{−216a^{12}}\)
    2. \(\sqrt[4]{486u^7}+\sqrt[4]{768u^3}\)
    Exemple\(\PageIndex{103}\)
    1. \(\sqrt[3]{80b^5}−\sqrt[3]{−270b^3}\)
    2. \(\sqrt[4]{160v^{10}}−\sqrt[4]{1280v^3}\)
    Réponse
    1. \(2b\sqrt[3]{10b^2}+3b\sqrt[3]{10}\)
    2. \(2v^2\sqrt[4]{10v^2}−4\sqrt[4]{5v^3}\)
    Pratique mixte

    Dans les exercices suivants, simplifiez.

    Exemple\(\PageIndex{104}\)

    \(\sqrt[4]{16}\)

    Exemple\(\PageIndex{105}\)

    \(\sqrt[6]{64}\)

    Réponse

    2

    Exemple\(\PageIndex{106}\)

    \(\sqrt[3]{a^3}\)

    Exemple\(\PageIndex{107}\)

    .

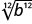
    Réponse

    |b|

    Exemple\(\PageIndex{108}\)

    \(\sqrt[3]{−8c^9}\)

    Exemple\(\PageIndex{109}\)

    \(\sqrt[3]{125d^{15}}\)

    Réponse

    \(5d^5\)

    Exemple\(\PageIndex{110}\)

    \(\sqrt[3]{r^5}\)

    Exemple\(\PageIndex{111}\)

    \(\sqrt[4]{s^{10}}\)

    Réponse

    \(s^2\sqrt[4]{s^2}\)

    Exemple\(\PageIndex{112}\)

    \(\sqrt[3]{108x^5}\)

    Exemple\(\PageIndex{113}\)

    \(\sqrt[4]{48y^6}\)

    Réponse

    \(2y\sqrt[4]{3y^2}\)

    Exemple\(\PageIndex{114}\)

    \(\sqrt[5]{−486}\)

    Exemple\(\PageIndex{115}\)

    \(\sqrt[6]{−64}\)

    Réponse

    pas réel

    Exemple\(\PageIndex{116}\)

    \(\frac{\sqrt[4]{64}}{\sqrt[4]{2}}\)

    Exemple\(\PageIndex{117}\)

    \(\frac{\sqrt[5]{128x^8}}{\sqrt[5]{2x^2}}\)

    Réponse

    \(2x\sqrt[5]{2x}\)

    Exemple\(\PageIndex{118}\)

    \(\sqrt[5]{\frac{96r^{11}}{s^3}}\)

    Exemple\(\PageIndex{119}\)

    \(\sqrt[6]{\frac{128u^7}{v^3}}\)

    Réponse

    \(\frac{2u^3\sqrt[6]{2uv^3}}{v}\)

    Exemple\(\PageIndex{120}\)

    \(\sqrt[3]{81}−\sqrt[3]{192}\)

    Exemple\(\PageIndex{121}\)

    \(\sqrt[4]{512}−\sqrt[4]{32}\)

    Réponse

    \(4\sqrt[4]{2}\)

    Exemple\(\PageIndex{122}\)

    \(\sqrt[3]{64a^{10}}−\sqrt[3]{−216a^{12}}\)

    Exemple\(\PageIndex{123}\)

    \(\sqrt[4]{486u^7}+\sqrt[4]{768u^3}\)

    Réponse

    \(3u\sqrt[4]{6u^3}+4\sqrt[4]{3u^3}\)

    Mathématiques quotidiennes

    Exemple\(\PageIndex{124}\)

    Croissance de la population L'expression\(10·x^n\) modélise la croissance d'une population de moisissures après n générations. Il y avait 10 spores au départ et chacune avait une progéniture. Il en\(10·x^n\) va de même pour le nombre de descendants à la cinquième génération. À la cinquième génération, il y avait 10 240 enfants. Simplifiez l'expression\(\sqrt[5]{\frac{10,240}{10}}\) pour déterminer le nombre de descendants de chaque spore.

    Exemple\(\PageIndex{125}\)

    Propagation d'un virus L'expression\(3·x^n\) modélise la propagation d'un virus après n cycles. Trois personnes étaient initialement infectées par le virus, et chacune d'elles a infecté x personnes. Il en\(3·x^4\) va de même pour le nombre de personnes infectées au quatrième cycle. Au quatrième cycle, 1875 personnes ont été infectées. Simplifiez l'expression\(\sqrt[4]{\frac{1875}{3}}\) pour déterminer le nombre de personnes infectées par chaque personne.

    Réponse

    5

    Exercices d'écriture

    Exemple\(\PageIndex{126}\)

    Expliquez comment vous le savez\(\sqrt[5]{x^{10}}=x^2\).

    Exemple\(\PageIndex{127}\)

    Expliquez pourquoi\(\sqrt[4]{−64}\) ce n'est pas un vrai nombre mais l'\(\sqrt[3]{−64}\)est.

    Réponse

    Les réponses peuvent varier.

    Auto-vérification

    ⓐ Une fois les exercices terminés, utilisez cette liste de contrôle pour évaluer votre maîtrise des objectifs de cette section.

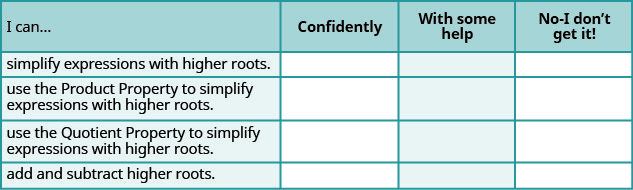
    Ce tableau comporte quatre colonnes et cinq lignes. La première rangée indique chaque colonne : « Je peux... », « En toute confiance », « Avec de l'aide » et « Non, je ne comprends pas ! » Les lignes sous la colonne « Je peux... » se lisent comme suit : « Simplifiez les expressions ayant des racines présentes », « Utilisez la propriété du produit pour simplifier les expressions ayant des racines supérieures », « Utilisez la propriété quotient pour simplifier les expressions ayant des racines plus hautes » et « Ajoutez et soustrayez des racines supérieures ». Les autres lignes situées sous les colonnes sont vides.

    ⓑ Que vous apprend cette liste de contrôle sur votre maîtrise de cette section ? Quelles mesures allez-vous prendre pour vous améliorer ?