Skip to main content
Global

6.6 : Diviser les polynômes

  1. Last updated
  2. Save as PDF
  • Page ID
    195004

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Objectifs d'apprentissage

    À la fin de cette section, vous serez en mesure de :

    • Diviser un polynôme par un monomial
    • Diviser un polynôme par un binôme
    Remarque

    Avant de commencer, répondez à ce questionnaire de préparation.

    1. Ajouter :\(\dfrac{3}{d}+\dfrac{x}{d}\)
      Si vous avez oublié ce problème, passez en revue l'exercice 1.7.1.
    2. Simplifier :\(\dfrac{30 x y^{3}}{5 x y}\)
      si vous avez oublié ce problème, passez en revue l'exercice 6.5.37.
    3. Combinez des termes similaires :\(8 a^{2}+12 a+1+3 a^{2}-5 a+4\)
      si vous avez oublié ce problème, passez en revue l'exercice 1.3.37.

    Diviser un polynôme par un monomial

    Dans la dernière section, vous avez appris à diviser un monôme par un monomial. Au fur et à mesure que vous approfondissez vos connaissances sur les polynômes, la procédure suivante consiste à diviser un polynôme de deux termes ou plus par un monôme.

    La méthode que nous utiliserons pour diviser un polynôme par un monomial est basée sur les propriétés de l'addition de fractions. Nous allons donc commencer par un exemple pour examiner l'ajout de fractions.

    \(\begin{array}{ll}{\text { The sum, }} & {\dfrac{y}{5}+\dfrac{2}{5}} \\ {\text { simplifies to }} & {\dfrac{y+2}{5}}\end{array}\)

    Nous allons maintenant procéder à l'inverse pour diviser une seule fraction en fractions distinctes.

    Nous allons énoncer la propriété d'addition de fractions ici telle que vous l'avez apprise et inversement.

    AJOUT DE FRACTIONS

    Si a, b et c sont des nombres où\(c\neq 0\), alors

    \[\dfrac{a}{c}+\dfrac{b}{c}=\dfrac{a+b}{c} \quad \text { and } \quad \dfrac{a+b}{c}=\dfrac{a}{c}+\dfrac{b}{c}\]

    Nous utilisons la forme de gauche pour ajouter des fractions et la forme de droite pour diviser un polynôme par un monomial.

    \(\begin{array}{ll}{\text { For example, }} & {\dfrac{y+2}{5}} \\ {\text { can be written }} & {\dfrac{y}{5}+\dfrac{2}{5}}\end{array}\)

    Nous utilisons cette forme d'addition de fractions pour diviser les polynômes par les monômes.

    DIVISION D'UN POLYNÔME PAR UN MONOMIAL

    Pour diviser un polynôme par un monomial, divisez chaque terme du polynôme par le monomial.

    Exercice\(\PageIndex{1}\)

    Trouvez le quotient :\(\dfrac{7 y^{2}+21}{7}\)

    Réponse

    \(\begin{array}{ll} & \dfrac{7 y^{2}+21}{7}\\\text{Divide each term of the numerator by the denominator.} & \dfrac{7 y^{2}}{7}+\dfrac{21}{7} \\ \text {Simplify each fraction. } & y^{2}+3 \end{array}\)

    Exercice\(\PageIndex{2}\)

    Trouvez le quotient :\(\dfrac{8 z^{2}+24}{4}\)

    Réponse

    \(2 z^{2}+6\)

    Exercice\(\PageIndex{3}\)

    Trouvez le quotient :\(\dfrac{18 z^{2}-27}{9}\)

    Réponse

    \(2 z^{2}-3\)

    N'oubliez pas que la division peut être représentée par une fraction. Lorsqu'on vous demande de diviser un polynôme par un monomial et qu'il n'est pas déjà sous forme de fraction, écrivez une fraction avec le polynôme dans le numérateur et le monomial dans le dénominateur.

    Exercice\(\PageIndex{4}\)

    Trouvez le quotient :\(\left(18 x^{3}-36 x^{2}\right) \div 6 x\)

    Réponse

    \(\begin{array}{ll} & \left(18 x^{3}-36 x^{2}\right) \div 6 x\\\text { Rewrite as a fraction. } & \dfrac{18 x^{3}-36 x^{2}}{6 x} \\ \text { Divide each term of the numerator by the denominator. }& \dfrac{18 x^{3}}{6 x}-\dfrac{36 x^{2}}{6 x}\\ \text { Simplify. } &3 x^{2}-6 x\end{array}\)

    Exercice\(\PageIndex{5}\)

    Trouvez le quotient :\(\left(27 b^{3}-33 b^{2}\right) \div 3 b\)

    Réponse

    \(9 b^{2}-11 b\)

    Exercice\(\PageIndex{6}\)

    Trouvez le quotient :\(\left(25 y^{3}-55 y^{2}\right) \div 5 y\)

    Réponse

    \(5 y^{2}-11 y\)

    Lorsque nous divisons par un négatif, nous devons faire très attention aux signes.

    Exercice\(\PageIndex{7}\)

    Trouvez le quotient :\(\dfrac{12 d^{2}-16 d}{-4}\)

    Réponse

    \(\begin{array}{ll} &\dfrac{12 d^{2}-16 d}{-4}\\ \text { Divide each term of the numerator by the denominator. }& \dfrac{18 x^{3}-36 x^{2}}{6 x} \\ \text { Simplify. Remember, subtracting a negative is like adding a positive! }& -3 d^{2}+4 d\end{array}\)

    Exercice\(\PageIndex{8}\)

    Trouvez le quotient :\(\dfrac{25 y^{2}-15 y}{-5}\)

    Réponse

    \(-5 y^{2}+3 y\)

    Exercice\(\PageIndex{9}\)

    Trouvez le quotient :\(\dfrac{42 b^{2}-18 b}{-6}\)

    Réponse

    \(-7 b^{2}+3 b\)

    Exercice\(\PageIndex{10}\)

    Trouvez le quotient :\(\dfrac{105 y^{5}+75 y^{3}}{5 y^{2}}\)

    Réponse

    \(\begin{array}{ll} &\dfrac{105 y^{5}+75 y^{3}}{5 y^{2}}\\ \text { Separate the terms. }& \dfrac{105 y^{5}}{5 y^{2}}+\dfrac{75 y^{3}}{5 y^{2}}\\ \text { Simplify. }& 21 y^{3}+15 y\end{array}\)

    Exercice\(\PageIndex{11}\)

    Trouvez le quotient :\(\dfrac{60 d^{7}+24 d^{5}}{4 d^{3}}\)

    Réponse

    \(15 d^{4}+6 d^{2}\)

    Exercice\(\PageIndex{12}\)

    Trouvez le quotient :\(\dfrac{216 p^{7}-48 p^{5}}{6 p^{3}}\)

    Réponse

    \(36 p^{4}-8 p^{2}\)

    Exercice\(\PageIndex{13}\)

    Trouvez le quotient :\(\left(15 x^{3} y-35 x y^{2}\right) \div(-5 x y)\)

    Réponse

    \(\begin{array}{ll} &\left(15 x^{3} y-35 x y^{2}\right) \div(-5 x y)\\ \text { Rewrite as a fraction. }& \dfrac{15 x^{3} y-35 x y^{2}}{-5 x y}\\\text { Separate the terms. Be careful with the signs! }& \dfrac{15 x^{3} y}{-5 x y}-\dfrac{35 x y^{2}}{-5 x y}\\ \text { Simplify. } & -3 x^{2}+7 y\end{array}\)

    Exercice\(\PageIndex{14}\)

    Trouvez le quotient :\(\left(32 a^{2} b-16 a b^{2}\right) \div(-8 a b)\)

    Réponse

    \(-4 a+2 b\)

    Exercice\(\PageIndex{15}\)

    Trouvez le quotient :\(\left(-48 a^{8} b^{4}-36 a^{6} b^{5}\right) \div\left(-6 a^{3} b^{3}\right)\)

    Réponse

    \(8 a^{5} b+6 a^{3} b^{2}\)

    Exercice\(\PageIndex{13}\)

    Trouvez le quotient :\(\dfrac{36 x^{3} y^{2}+27 x^{2} y^{2}-9 x^{2} y^{3}}{9 x^{2} y}\)

    Réponse

    \(\begin{array}{ll} &\dfrac{36 x^{3} y^{2}+27 x^{2} y^{2}-9 x^{2} y^{3}}{9 x^{2} y}\\\text { Separate the terms. }& \dfrac{36 x^{3} y^{2}}{9 x^{2} y}+\dfrac{27 x^{2} y^{2}}{9 x^{2} y}-\dfrac{9 x^{2} y^{3}}{9 x^{2} y}\\ \text { Simplify. } & 4 x y+3 y-y^{2}\end{array}\)

    Exercice\(\PageIndex{14}\)

    Trouvez le quotient :\(\dfrac{40 x^{3} y^{2}+24 x^{2} y^{2}-16 x^{2} y^{3}}{8 x^{2} y}\)

    Réponse

    \(5 x y+3 y-2 y^{2}\)

    Exercice\(\PageIndex{15}\)

    Trouvez le quotient :\(\dfrac{35 a^{4} b^{2}+14 a^{4} b^{3}-42 a^{2} b^{4}}{7 a^{2} b^{2}}\)

    Réponse

    \(5 a^{2}+2 a^{2} b-6 b^{2}\)

    Exercice\(\PageIndex{16}\)

    Trouvez le quotient :\(\dfrac{10 x^{2}+5 x-20}{5 x}\)

    Réponse

    \(\begin{array}{ll}&\dfrac{10 x^{2}+5 x-20}{5x}\\\text { Separate the terms. }& \dfrac{10 x^{2}}{5 x}+\dfrac{5 x}{5 x}-\dfrac{20}{5 x}\\ \text { Simplify. } &2 x+1-\dfrac{4}{x}\end{array}\)

    Exercice\(\PageIndex{17}\)

    Trouvez le quotient :\(\dfrac{18 c^{2}+6 c-9}{6 c}\)

    Réponse

    \(3 c+1-\dfrac{3}{2 c}\)

    Exercice\(\PageIndex{18}\)

    Trouvez le quotient :\(\dfrac{10 d^{2}-5 d-2}{5 d}\)

    Réponse

    \(2 d-1-\dfrac{2}{5 d}\)

    Diviser un polynôme par un binôme

    Pour diviser un polynôme par un binôme, nous suivons une procédure très similaire à la division longue des nombres. Examinons donc attentivement les étapes à suivre lorsque nous divisons un nombre à 3 chiffres, 875, par un nombre à 2 chiffres, 25.

    Nous écrivons la division longue 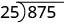La division longue de 875 par 25.
    Nous divisons les deux premiers chiffres, 87, par 25. 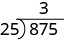25 correspond à 87 trois fois. 3 est écrit au-dessus du deuxième chiffre de 875 dans la parenthèse longue.
    Nous multiplions 3 fois 25 et écrivons le produit sous le 87. 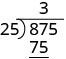Le produit de 3 et 25 est 75, ce qui est écrit en dessous des deux premiers chiffres de 875 dans la parenthèse longue.
    Maintenant, nous soustrayons 75 de 87. 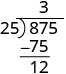87 moins 75 est 12, ce qui est écrit sous 75.
    Ensuite, nous abaissons le troisième chiffre du dividende, 5. 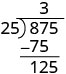Le 5 en 875 est abaissé à côté du 12, soit 125.
    Répétez l'opération en divisant 25 en 125. 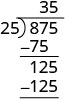25 correspond à 125 cinq fois. 5 est écrit à droite du 3 en haut du crochet de division longue. 5 fois 25 vaut 125. 125 moins 125 est zéro. Il n'y a aucun reste, donc 25 correspond exactement à 125 cinq fois. 875 divisé par 25 équivaut à 35.

    On vérifie la division en multipliant le quotient par le diviseur.

    Si nous avons fait la division correctement, le produit devrait être égal au dividende.

    \[\begin{array}{l}{35 \cdot 25} \\ {875}\checkmark\end{array}\]

    Nous allons maintenant diviser un trinôme par un binôme. En lisant l'exemple, vous remarquerez à quel point les étapes sont similaires à celles de l'exemple numérique ci-dessus.

    Exercice\(\PageIndex{19}\)

    Trouvez le quotient :\(\left(x^{2}+9 x+20\right) \div(x+5)\)

    Réponse
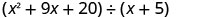
      Un trinôme, x au carré plus 9 x plus 20, divisé par un binôme, x plus 5.
    Écrivez-le comme un problème de division longue.  
    Assurez-vous que le dividende est sous forme standard. 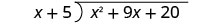La division longue de x au carré plus 9 x plus 20 par x plus 5
    Divisez x 2 par x. Il peut être utile de se demander : « De quoi ai-je besoin pour multiplier x pour obtenir x 2 ? »  
    Mettez la réponse, x, dans le quotient sur le terme x. 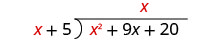x correspond à x au carré x fois. x est écrit au-dessus du deuxième terme de x au carré plus 9 x plus 20 dans la parenthèse longue.
    Multipliez x fois x + 5. Alignez les conditions similaires sous le dividende. 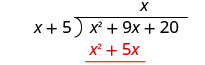Le produit de x et x plus 5 est x au carré plus 5 x, ce qui est écrit sous les deux premiers termes de x au carré plus 9x plus 20 dans la parenthèse de division longue.
    Soustrayez x 2 + 5 x de x 2 + 9 x.  
    Il vous sera peut-être plus facile de modifier les signes, puis de les ajouter.
    Ensuite, réduisez le dernier mandat, 20.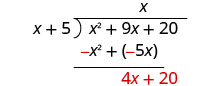    		 La somme de x au carré plus 9 x et de moins x au carré plus moins 5 x est 4 x, ce qui est écrit sous le négatif 5 x. Le troisième terme en x carré plus 9 x plus 20 est ramené à côté de 4 x, soit 4 x plus 20.
    Divisez 4 x par x. Il peut être utile de se demander : « De quoi ai-je besoin pour
    multiplier x pour obtenir 4 x ? »    		  
    Mettez la réponse, 4, dans le quotient sur le terme constant. 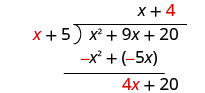4 x divisé par x est 4. Plus 4 est écrit en haut de la parenthèse longue, à côté de x et au-dessus des 20 pouces x au carré plus 9 x plus 20.
    Multipliez 4 fois x + 5. 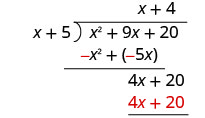x plus 5 fois 4 correspond à 4 x plus 20, qui est écrit sous le premier 4 x plus 20.
    Soustrayez 4 x + 20 de 4 x + 20. 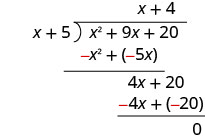4 x plus 20 moins 4 x plus 20 vaut 0. Le reste est égal à 0. x au carré plus 9 x plus 20 divisé par x plus 5 équivaut à x plus 4.
    Vérifiez :  
    Multipliez le quotient par le diviseur.  
    (x + 4) (x + 5)  
    Tu devrais toucher le dividende.  
    x 2 + 9 x + 20 ✓
    Exercice\(\PageIndex{20}\)

    Trouvez le quotient :\(\left(y^{2}+10 y+21\right) \div(y+3)\)

    Réponse

    y+7

    Exercice\(\PageIndex{21}\)

    Trouvez le quotient :\(\left(m^{2}+9 m+20\right) \div(m+4)\)

    Réponse

    m+5

    Lorsque le diviseur a un signe de soustraction, nous devons être très prudents lorsque nous multiplions le quotient partiel puis que nous le soustrayons. Il serait peut-être plus prudent de montrer que nous changeons les panneaux et que nous les ajoutons ensuite.

    Exercice\(\PageIndex{22}\)

    Trouvez le quotient :\(\left(2 x^{2}-5 x-3\right) \div(x-3)\)

    Réponse
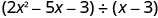
      Un trinôme, 2 x au carré moins 5 x moins 3, divisé par un binôme, x moins 3.
    Écrivez-le comme un problème de division longue.  
    Assurez-vous que le dividende est sous forme standard. 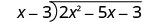La division longue de 2 x au carré moins 5 x moins 3 par x moins 3.
    Divisez 2 x 2 par x.
    Mettez la réponse, 2 x, dans le quotient sur le terme x.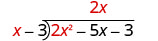    		 x correspond à 2 x au carré 2 x fois. 2 x est écrit au-dessus du deuxième terme, 2 x au carré moins 5 x moins 3 dans le crochet de division longue.
    Multipliez 2 x fois x − 3. Alignez les conditions similaires sous le dividende. 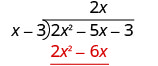Le produit de 2 x et x moins 3 est 2 x au carré moins 6 x, ce qui est écrit en dessous des deux premiers termes de 2 x au carré moins 5 x moins 3 dans la parenthèse longue.
    Soustrayez 2 x 2 − 6 x de 2 x 2 − 5 x.
    Changez les signes, puis ajoutez-les.
    Ensuite, annulez le dernier mandat.    		 La somme de 2 x au carré moins 5 x et de moins 2 x au carré plus 6 x est x, qui est écrit sous le 6 x. Le troisième terme de 2 x au carré moins 5 x moins 3 est abaissé à côté de x, ce qui fait x moins 3.
    Divisez x par x.
    Mettez la réponse, 1, dans le quotient sur le terme constant.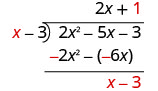    		 Plus 1 est écrit au-dessus de la parenthèse longue, à côté de 2 x et au-dessus du moins 3 sur 2 x au carré moins 5 x moins 3.
    Multipliez 1 fois x − 3. 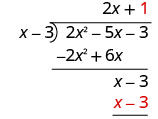x moins 3 fois 1 est x moins 3, qui est écrit sous le premier x moins 3.
    Soustrayez x − 3 de x − 3 en modifiant les signes et en ajoutant. 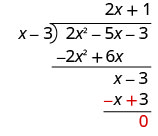Le binôme x moins 3 moins le binôme négatif x plus 3 vaut 0. Le reste est égal à 0. 2 x au carré moins 5 x moins 3 divisé par x moins 3 équivaut à 2 x plus 1.
    Pour vérifier, multipliez (x − 3) (2 x + 1).  
    Le résultat doit être 2 x 2 − 5 x − 3.
    Exercice\(\PageIndex{23}\)

    Trouvez le quotient :\(\left(2 x^{2}-3 x-20\right) \div(x-4)\)

    Réponse

    2x+5

    Exercice\(\PageIndex{24}\)

    Trouvez le quotient :\(\left(3 x^{2}-16 x-12\right) \div(x-6)\)

    Réponse

    3x+2

    Lorsque nous avons divisé 875 par 25, nous n'avions plus de reste. Mais parfois, la division des nombres laisse du reste. Il en va de même lorsque nous divisons des polynômes. Dans Exercice\(\PageIndex{25}\), nous aurons une division qui laissera le reste. Nous écrivons le reste sous forme de fraction avec le diviseur comme dénominateur.

    Exercice\(\PageIndex{25}\)

    Trouvez le quotient :\(\left(x^{3}-x^{2}+x+4\right) \div(x+1)\)

    Réponse
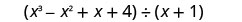
      Un polynôme, x cubique moins x carré plus x plus 4, divisé par un autre polynôme, x plus 1.
    Écrivez-le comme un problème de division longue.  
    Assurez-vous que le dividende est sous forme standard. 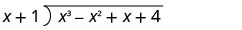La division longue de x au cube moins x au carré plus x plus 4 par x plus 1.
    Divisez x 3 par x.
    Inscrivez la réponse, x 2, dans le quotient sur le terme x 2.
    Multipliez x 2 fois x +1. Alignez les conditions similaires sous le dividende.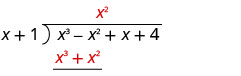    		 x correspond à x au carré x fois. x est écrit au-dessus du deuxième terme de x cube moins x carré plus x plus 4 dans la parenthèse de division longue.
    Soustrayez x 3 + x 2 de x 3 − x 2 en modifiant les signes et en ajoutant.
    Ensuite, réduisez le mandat suivant.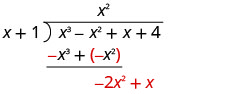    		 La somme de x cube moins x au carré et de moins x au cube et de moins x au carré est moins 2 x au carré, ce qui est écrit sous le x au carré négatif. Le terme suivant en x cube moins x au carré plus x plus 4 est abaissé à côté de moins 2 x au carré, ce qui donne moins 2 x au carré plus x.
    Divisez −2 x 2 par x.
    Mettez la réponse, −2 x, dans le quotient sur le terme x.
    Multipliez −2 x fois x +1. Alignez les conditions similaires sous le dividende.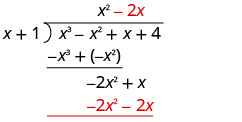    		 Moins 2 x est écrit au-dessus du crochet de division longue, à côté de x au carré et au-dessus du x en x cubique moins x au carré plus x plus 4. Négatif 2 x au carré moins 2 x s'écrit sous moins 2 x au carré plus x.
    Soustrayez −2 x 2 − 2 x de −2 x 2 + x en modifiant les signes et en ajoutant.
    Ensuite, annulez le dernier mandat.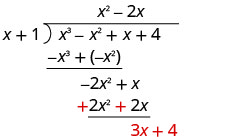    		 La somme de moins 2 x au carré plus x et de 2 x au carré plus 2 x est trouvée comme étant 3 x. Le dernier terme en x cubique moins x au carré plus x plus 4 est réduit, soit 3 x plus 4.
    Divisez 3 x par x.
    Mettez la réponse, 3, dans le quotient sur le terme constant.
    Multipliez 3 fois x +1. Alignez les conditions similaires sous le dividende.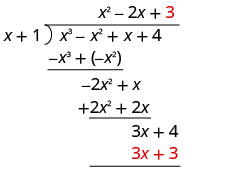    		 Plus 3 est écrit au-dessus du crochet de division long, au-dessus du carré de 4 pouces x moins x carré plus x plus 4. 3 x plus 3 est écrit sous 3 x plus 4.
    Soustrayez 3 x + 3 de 3 x + 4 en modifiant les signes et en ajoutant.
    Écrivez le reste sous forme de fraction avec le diviseur comme dénominateur.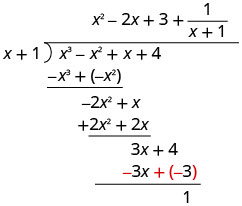    		 La somme de 3 x plus 4 et de moins 3 x plus moins 3 est égale à 1. Par conséquent, le polynôme x cubique moins x carré plus x plus 4, divisé par le binôme x plus 1, est égal à x carré moins 2 x plus la fraction 1 sur x plus 1.
    Pour vérifier, multipliez\((x+1)\left(x^{2}-2 x+3+\dfrac{1}{x+1}\right)\)
    Le résultat doit être\(x^{3}-x^{2}+x+4\)
    Exercice\(\PageIndex{26}\)

    Trouvez le quotient :\(\left(x^{3}+5 x^{2}+8 x+6\right) \div(x+2)\)

    Réponse

    \(x^{2}+3 x+2+\dfrac{2}{x+2}\)

    Exercice\(\PageIndex{27}\)

    Trouvez le quotient :\(\left(2 x^{3}+8 x^{2}+x-8\right) \div(x+1)\)

    Réponse

    \(2 x^{2}+6 x-5-\dfrac{3}{x+1}\)

    Examinez les dividendes dans Exemple, Exemple et Exemple. Les termes étaient écrits par ordre décroissant de degrés et aucun diplôme ne manquait. Le dividende dans Example sera de\(x^{4}-x^{2}+5 x-2\). Il manque un\(x^{3}\) terme. Nous l'ajouterons en\(0x^{3}\) tant qu'espace réservé.

    Exercice\(\PageIndex{28}\)

    Trouvez le quotient :\(\left(x^{4}-x^{2}+5 x-2\right) \div(x+2)\)

    Réponse

    Notez qu'il n'y a pas de\(x^{3}\) terme dans le dividende. Nous l'ajouterons\(0x^{3}\) comme espace réservé.

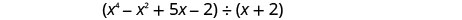
      Un polynôme, x à la quatrième puissance moins x au carré moins 5 x moins 2, divisé par un autre polynôme, x plus 2.
    Écrivez-le comme un problème de division longue. Assurez-vous que le dividende est sous une forme standard avec des espaces réservés pour les termes manquants. 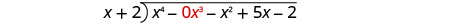La division longue de x à la quatrième puissance plus 0 x cubique moins x au carré moins 5 x moins 2 par x plus 2.
    Divisez x 4 par x.
    Inscrivez la réponse, x 3, dans le quotient sur le terme x 3.
    Multipliez x 3 fois x + 2. Alignez les termes similaires.
    Soustrayez puis réduisez le terme suivant.    		 x cubed est écrit au-dessus de la tranche de division longue au-dessus du terme x cubed du dividende. En dessous des deux premiers termes du dividende, x à la quatrième puissance plus 2 x cube est soustrait pour donner moins 2 x cube moins x au carré. Une note à côté de la division se lit comme suit : « Il peut être utile de modifier les panneaux et d'ajouter ».
    Divisez −2 x 3 par x.
    Mettez la réponse, −2 x 2, dans le quotient sur le terme x 2.
    Multipliez −2 x 2 fois x +1. Alignez les termes similaires.
    Soustrayez et réduisez le terme suivant.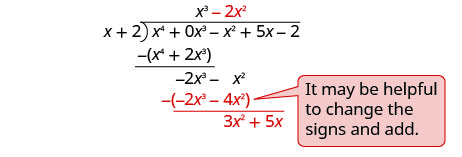    		 x cube moins 2 x carré est écrit en haut du crochet de division long. Au bas de la division longue, le négatif 2 x cube moins 4 x carré est soustrait pour donner 3 x au carré plus 5 x. Une note indique « Il peut être utile de changer les signes et d'ajouter ».
    Divisez 3 x 2 par x.
    Mettez la réponse, 3 x, dans le quotient sur le terme x.
    Multipliez 3 x fois x +1. Alignez les termes similaires.
    Soustrayez et réduisez le terme suivant.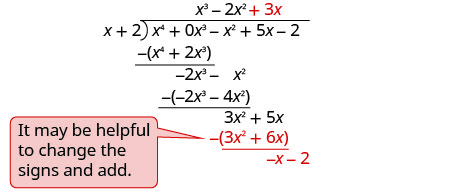    		 x cube moins 2 x carré plus 3 x est écrit au-dessus du crochet de division long. Au bas de la division longue, 3 x le carré plus 6 x sont soustraits pour donner un x moins 2 négatif. Une note indique : « Il peut être utile de modifier les panneaux et d'en ajouter ».
    Diviser − x par x.
    Mettez la réponse, −1, dans le quotient sur le terme constant.
    Multipliez −1 fois x +1. Alignez les termes similaires.
    Changez les signes, ajoutez.    		 x cube moins 2 x carré plus 3 x moins 1 est écrit au-dessus du crochet de division long. Au bas de la division longue, on soustrait x moins 2 pour obtenir 0. Une note indique : « Il peut être utile de modifier les panneaux et d'en ajouter ». Le polynôme x à la quatrième puissance moins x au carré plus 5 x moins 2, divisé par le binôme x plus 2 est égal au polynôme x au cube moins 2 x au carré plus 3 x moins 1.
    Pour vérifier, multipliez\((x+2)\left(x^{3}-2 x^{2}+3 x-1\right)\)  
    Le résultat doit être\(x^{4}-x^{2}+5 x-2\)
    Exercice\(\PageIndex{29}\)

    Trouvez le quotient :\(\left(x^{3}+3 x+14\right) \div(x+2)\)

    Réponse

    \(x^{2}-2 x+7\)

    Exercice\(\PageIndex{30}\)

    Trouvez le quotient :\(\left(x^{4}-3 x^{3}-1000\right) \div(x+5)\)

    Réponse

    \(x^{3}-8 x^{2}+40 x-200\)

    Dans Exercice\(\PageIndex{31}\), nous allons diviser par\(2a−3\). Lorsque nous divisons, nous devrons prendre en compte les constantes ainsi que les variables.

    Exercice\(\PageIndex{31}\)

    Trouvez le quotient :\(\left(8 a^{3}+27\right) \div(2 a+3)\)

    Réponse

    Cette fois, nous allons montrer la division en une seule étape. Nous devons ajouter deux espaces réservés pour diviser.

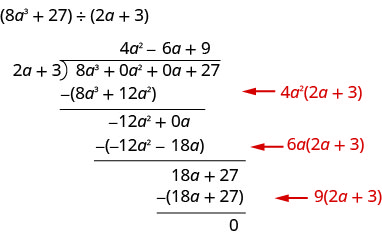
    La figure montre la division longue de 8 un cube plus 27 par 2 a plus 3. Dans la parenthèse longue, les espaces réservés 0 au carré et 0 a sont ajoutés au polynôme. Sur la première ligne, sous le dividende 8, un cube plus 12 au carré est soustrait. À droite, une flèche indique que cette valeur provient de la multiplication de 4 au carré par 2 a plus 3. La soustraction donne moins 12 au carré plus 0 a. De ce négatif 12, on soustrait un carré moins 18 a. À droite, une flèche indique que cette valeur provient de la multiplication de 6 a par 2 a plus 3. La soustraction donne 18 a plus 27. De ce 18, on soustrait un plus 27. À droite, une flèche indique que cette valeur provient de la multiplication de 9 par 2 a plus 3. Le résultat est 0.

    Pour vérifier, multipliez\((2 a+3)\left(4 a^{2}-6 a+9\right)\)

    Le résultat doit être\(8 a^{3}+27\)

    Exercice\(\PageIndex{32}\)

    Trouvez le quotient :\(\left(x^{3}-64\right) \div(x-4)\)

    Réponse

    \(x^{2}+4 x+16\)

    Exercice\(\PageIndex{33}\)

    Trouvez le quotient :\(\left(125 x^{3}-8\right) \div(5 x-2)\)

    Réponse

    \(25 x^{2}+10 x+4\)

    Remarque

    Accédez à ces ressources en ligne pour obtenir des instructions et des exercices supplémentaires sur la division de polynômes :

    • Diviser un polynôme par un monomial
    • Diviser un polynôme par un monomial 2
    • Diviser un polynôme par un binôme

    Concepts clés

    • Addition de fractions
      • Si a, b et c sont des nombres où\(c\neq 0\), alors
        \(\dfrac{a}{c}+\dfrac{b}{c}=\dfrac{a+b}{c}\) et\(\dfrac{a+b}{c}=\dfrac{a}{c}+\dfrac{b}{c}\)
    • Division d'un polynôme par un monomial
      • Pour diviser un polynôme par un monomial, divisez chaque terme du polynôme par le monomial.