6.5 : Diviser les monômes
- Page ID
- 195052
À la fin de cette section, vous serez en mesure de :
- Simplifier les expressions à l'aide de la propriété quotient pour les expos
- Simplifiez les expressions avec zéro exposant
- Simplifier les expressions à l'aide du quotient d'une propriété de puissance
- Simplifier les expressions en appliquant plusieurs propriétés
- Diviser les monômes
Avant de commencer, répondez à ce questionnaire de préparation.
- Simplifiez :\(\dfrac{8}{24}\).
Si vous avez oublié ce problème, passez en revue l'exercice 1.6.4. - Simplifiez :\((2m^3)^5\).
Si vous avez oublié ce problème, passez en revue l'exercice 6.2.22. - Simplifier :\(\dfrac{12x}{12y}\)
si vous avez oublié ce problème, passez en revue l'exercice 1.6.10.
Simplifier les expressions en utilisant la propriété de quotient pour les exposants
Plus tôt dans ce chapitre, nous avons développé les propriétés des exposants pour la multiplication. Nous résumons ces propriétés ci-dessous.
Si a et b sont des nombres réels, et m et n sont des nombres entiers, alors
\[\begin{array}{ll}{\textbf { Product Property }} & {a^{m} \cdot a^{n}=a^{m+n}} \\ {\textbf { Power Property }} & {\left(a^{m}\right)^{n}=a^{m n}} \\ {\textbf { Product to a Power }} & {(a b)^{m}=a^{m} b^{m}}\end{array}\]
Nous allons maintenant examiner les propriétés des exposants pour la division. Un rappel rapide de la mémoire peut être utile avant de commencer. Vous avez appris à simplifier les fractions en séparant les facteurs communs du numérateur et du dénominateur à l'aide de la propriété des fractions équivalentes. Cette propriété vous aidera également à travailler avec les fractions algébriques, qui sont également des quotients.
Si a, b et c sont des nombres entiers où\(b\neq 0,c\neq 0\).
\[\text{then} \quad \dfrac{a}{b}=\dfrac{a \cdot c}{b \cdot c} \quad \text{and} \quad \dfrac{a \cdot c}{b \cdot c}=\dfrac{a}{b}\]
Comme précédemment, nous allons essayer de découvrir une propriété à l'aide de quelques exemples.
\[\begin{array}{lclc}{\text { Consider }} & \dfrac{x^{5}}{x^{2}} & \text{and} & \dfrac{x^{2}}{x^{3}}\\ {\text { What do they mean? }}&\dfrac{x \cdot x \cdot x \cdot x \cdot x}{x \cdot x} && \dfrac{x \cdot x}{x \cdot x \cdot x}\\ {\text { Use the Equivalent Fractions Property. }} & {\dfrac{x \not\cdot x \not\cdot x \cdot x \cdot x}{x \not\cdot\not x}} && \dfrac{\not x \cdot\not x \cdot 1}{x \not \cdot\not x \cdot x}\\ {\text { Simplify. }} & {x^{3}} & & \dfrac{1}{x}\end{array}\]
Remarquez que dans chaque cas, les bases étaient les mêmes et nous avons soustrait des exposants.
Lorsque le plus grand exposant se trouvait dans le numérateur, il nous restait des facteurs dans le numérateur.
Lorsque le plus grand exposant se trouvait dans le dénominateur, il ne nous restait que des facteurs dans le dénominateur : notez le numérateur de 1.
Nous écrivons :
\[\begin{array}{cc}{\dfrac{x^{5}}{x^{2}}} & {\dfrac{x^{2}}{x^{3}}} \\ {x^{5-2}} & {\dfrac{1}{x^{3-2}}} \\ {x^{3}} & {\dfrac{1}{x}}\end{array}\]
Cela conduit à la propriété du quotient pour les exposants.
Si a est un nombre réel et que m et n sont des nombres entiers, alors\(a\neq 0\)
\[\dfrac{a^{m}}{a^{n}}=a^{m-n}, m>n \text { and } \dfrac{a^{m}}{a^{n}}=\dfrac{1}{a^{n-m}}, n>m\]
Quelques exemples avec des chiffres peuvent aider à vérifier cette propriété.
\[\begin{array} {llllll} \dfrac{3^{4}}{3^{2}} &=&3^{4-2}& \dfrac{5^{2}}{5^{3}} &=&\dfrac{1}{5^{3-2}} \\ \dfrac{81}{9} &=&3^{2} & \dfrac{25}{125} &=&\dfrac{1}{5^{1}} \\ 9 &=&9\checkmark& \dfrac{1}{5} &=&\dfrac{1}{5} \checkmark \end{array}\]
Simplifiez :
- \(\dfrac{x^{9}}{x^{7}}\)
- \(\dfrac{3^{10}}{3^{2}}\)
- Réponse
-
Pour simplifier une expression avec un quotient, nous devons d'abord comparer les exposants du numérateur et du dénominateur.
1.
Comme 9 > 7, il y a plus de facteurs de x dans le numérateur. 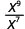
Utilisez la propriété du quotient,\(\dfrac{a^{m}}{a^{n}}=a^{m-n}\) 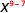
Simplifiez. \(x^2\) 2.
Notez que lorsque le plus grand exposant se trouve dans le numérateur, il nous reste des facteurs dans le numérateur.Comme 10 > 2, il y a plus de facteurs de x dans le numérateur. 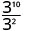
Utilisez la propriété du quotient,\(\dfrac{a^{m}}{a^{n}}=a^{m-n}\) 
Simplifiez. \(3^8\)
Simplifiez :
- \(\dfrac{x^{15}}{x^{10}}\)
- \(\dfrac{6^{14}}{6^{5}}\)
- Réponse
-
- \(x^{5}\)
- \(6^9\)
Simplifiez :
- \(\dfrac{y^{43}}{y^{37}}\)
- \(\dfrac{10^{15}}{10^{7}}\)
- Réponse
-
- \(y^{6}\)
- \(10^8\)
Simplifiez :
- \(\dfrac{b^{8}}{b^{12}}\)
- \(\dfrac{7^{3}}{7^{5}}\)
- Réponse
-
Pour simplifier une expression avec un quotient, nous devons d'abord comparer les exposants du numérateur et du dénominateur.
1.
Puisque 12 > 8, il y a plus de facteurs de b dans le dénominateur. 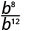
Utilisez la propriété du quotient,\(\dfrac{a^{m}}{a^{n}}=\dfrac{1}{a^{n-m}}\) 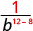
Simplifiez. 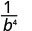
2.
Notez que lorsque le plus grand exposant se trouve dans le dénominateur, il nous reste des facteurs dans le dénominateur.Puisque 5 > 3, il y a plus de facteurs de 3 dans le dénominateur. 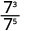
Utilisez la propriété du quotient,\(\dfrac{a^{m}}{a^{n}}=\dfrac{1}{a^{n-m}}\) 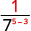
Simplifiez. 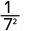
Simplifiez. 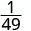
Simplifiez :
- \(\dfrac{x^{18}}{x^{22}}\)
- \(\dfrac{12^{15}}{12^{30}}\)
- Réponse
-
- \(\dfrac{1}{x^{4}}\)
- \(\dfrac{1}{12^{15}}\)
Simplifiez :
- \(\dfrac{m^{7}}{m^{15}}\)
- \(\dfrac{9^{8}}{9^{19}}\)
- Réponse
-
- \(\dfrac{1}{m^{8}}\)
- \(\dfrac{1}{9^{11}}\)
Remarquez la différence entre les deux exemples précédents :
- Si nous commençons avec plus de facteurs dans le numérateur, nous finirons par avoir des facteurs dans le numérateur.
- Si nous commençons avec plus de facteurs au dénominateur, nous finirons par avoir des facteurs au dénominateur.
La première étape de la simplification d'une expression à l'aide de la propriété Quotient pour les exposants consiste à déterminer si l'exposant est plus grand au numérateur ou au dénominateur.
Simplifiez :
- \(\dfrac{a^{5}}{a^{9}}\)
- \(\dfrac{x^{11}}{x^{7}}\)
- Réponse
-
1. L'exposant d'un plus grand est-il dans le numérateur ou le dénominateur ? Comme 9 > 5, il y a plus de a dans le dénominateur et nous allons donc obtenir des facteurs dans le dénominateur.
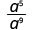
Utilisez la propriété du quotient,\(\dfrac{a^{m}}{a^{n}}=\dfrac{1}{a^{n-m}}\) 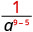
Simplifiez. 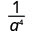
2. Notez qu'il y a plus de facteurs xx dans le numérateur, puisque 11 > 7. Nous allons donc nous retrouver avec des facteurs dans le numérateur.
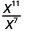
Utilisez la propriété du quotient,\(\dfrac{a^{m}}{a^{n}}=\dfrac{1}{a^{n-m}}\) 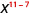
Simplifiez. 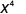
Simplifiez :
- \(\dfrac{b^{19}}{b^{11}}\)
- \(\dfrac{z^{5}}{z^{11}}\)
- Réponse
-
- \(b^{8}\)
- \(\dfrac{1}{z^{6}}\)
Simplifiez :
- \(\dfrac{p^{9}}{p^{17}}\)
- \(\dfrac{w^{13}}{w^{9}}\)
- Réponse
-
- \(\dfrac{1}{p^{8}}\)
- \(w^{4}\)
Simplifier les expressions avec un exposant égal à zéro
Un cas particulier de la propriété du quotient est celui où les exposants du numérateur et du dénominateur sont égaux, comme dans le cas d'une expression telle que\(\dfrac{a^{m}}{a^{m}}\). D'après vos travaux antérieurs sur les fractions, vous savez que :
\[\dfrac{2}{2}=1 \quad \dfrac{17}{17}=1 \quad \dfrac{-43}{-43}=1\]
En d'autres termes, un nombre divisé par lui-même vaut 1. Donc\(\dfrac{x}{x}=1\), pour tout\(x(x\neq 0)\), puisque tout nombre divisé par lui-même est 1.
La propriété du quotient pour les exposants nous montre comment simplifier le\(\dfrac{a^{m}}{a^{n}}\) moment\(m>n\) et le moment\(n<m\) en soustrayant des exposants. Et si\(m=n\) ?
Considérez\(\dfrac{8}{8}\), dont nous savons qu'il s'agit de 1.
\(\begin{array} {lrll} & \dfrac{8}{8} &=&1 \\ \text { Write } 8 \text { as } 2^{3} . & \dfrac{2^{3}}{2^{3}} &=&1 \\ \text { Subtract exponents. } & 2^{3-3} &=&1 \\ \text { Simplify. } & 2^{0} &=&1 \end{array}\)
Nous allons maintenant simplifier de deux\(\dfrac{a^{m}}{a^{m}}\) manières pour nous amener à la définition de l'exposant zéro. En général, pour\(a\neq 0\) :
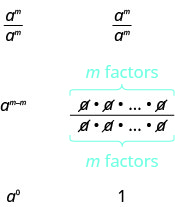
Nous voyons des\(\dfrac{a^{m}}{a^{m}}\) simplifications vers\(a^{0}\) et vers 1. Donc\(a^{0} = 1\).
Si a est un nombre différent de zéro, alors\(a^{0} = 1\).
Tout nombre différent de zéro élevé à la puissance zéro vaut 1.
Dans ce texte, nous supposons que toute variable que nous élevons à la puissance zéro n'est pas nulle.
Simplifiez :
- \(9^{0}\)
- \(n^{0}\)
- Réponse
-
La définition indique que tout nombre différent de zéro élevé à la puissance zéro est 1.
- \(\begin{array}{ll} & 9^0\\ \text{Use the definition of the zero exponent.} & 1 \end{array}\)
- \(\begin{array}{ll} & n^0\\ \text{Use the definition of the zero exponent.} & 1 \end{array}\)
Simplifiez :
- \(15^{0}\)
- \(m^{0}\)
- Réponse
-
- 1
- 1
Simplifiez :
- \(k^{0}\)
- \(29^{0}\)
- Réponse
-
- 1
- 1
Maintenant que nous avons défini l'exposant zéro, nous pouvons étendre toutes les propriétés des exposants pour inclure des exposants entiers.
Que diriez-vous d'élever une expression à la puissance zéro ? Regardons\((2x)^0\). Nous pouvons utiliser le produit à une règle de puissance pour réécrire cette expression.
\[\begin{array}{ll} & (2x)^0\\ {\text { Use the product to a power rule. }} & {2^{0} x^{0}} \\ {\text { Use the zero exponent property. }} & {1 \cdot 1} \\ {\text { Simplify. }} & 1\end{array}\]
Cela nous indique que toute expression non nulle élevée à la puissance zéro est une.
Simplifiez :
- \((5b)^0\)
- \((−4a^{2}b)^0\).
- Réponse
-
- \(\begin{array}{ll} & (5b)^0\\ {\text {Use the definition of the zero exponent.}} & 1\end{array}\)
- \(\begin{array}{ll} & (−4a^{2}b)^0\\ {\text {Use the definition of the zero exponent.}} & 1\end{array}\)
Simplifiez :
- \((11z)^0\)
- \((−11pq^{3})^0\).
- Réponse
-
- 1
- 1
Simplifiez :
- \((-6d)^0\)
- \((−8m^{2}n^{3})^0\).
- Réponse
-
- 1
- 1
Simplifier les expressions à l'aide du quotient d'une propriété de puissance
Nous allons maintenant examiner un exemple qui nous mènera au quotient d'une propriété énergétique.
\[\begin{array}{lc} & {\left(\dfrac{x}{y}\right)^{3}} \\ \text{This means:} & {\dfrac{x}{y} \cdot \dfrac{x}{y} \cdot \dfrac{x}{y}} \\ \text{Multiply the fractions.} &{\dfrac{x \cdot x \cdot x}{y \cdot y \cdot y}} \\ \text{Write with exponents.} & {\dfrac{x^{3}}{y^{3}}}\end{array}\]
Notez que l'exposant s'applique à la fois au numérateur et au dénominateur.
\[\begin{array}{lc}{\text { We see that }\left(\dfrac{x}{y}\right)^{3} \text { is } \dfrac{x^{3}}{y^{3}}} \\ {\text { We write: }} & \left(\dfrac{x}{y}\right)^{3} \\ & {\dfrac{x^{3}}{y^{3}}} \end{array}\]
Cela conduit au quotient d'une propriété de puissance pour les exposants.
Si a et b sont des nombres réels et que m est un nombre de comptage, alors\(b\neq 0\)
\[\left(\dfrac{a}{b}\right)^{m}=\dfrac{a^{m}}{b^{m}}\]
Pour élever une fraction à une puissance, augmentez le numérateur et le dénominateur à cette puissance.
Un exemple avec des chiffres peut vous aider à comprendre cette propriété :
\[\begin{aligned}\left(\dfrac{2}{3}\right)^{3} &=\dfrac{2^{3}}{3^{3}} \\ \dfrac{2}{3} \cdot \dfrac{2}{3} \cdot \dfrac{2}{3} &=\dfrac{8}{27} \\ \dfrac{8}{27} &=\dfrac{8}{27}\checkmark \end{aligned}\]
Simplifiez :
- \(\left(\dfrac{3}{7}\right)^{2}\)
- \(\left(\dfrac{b}{3}\right)^{4}\)
- \(\left(\dfrac{k}{j}\right)^{3}\)
- Réponse
-
1.
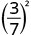
Utilisez la propriété du quotient,\(\left(\dfrac{a}{b}\right)^{m}=\dfrac{a^{m}}{b^{m}}\) 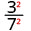
Simplifiez. 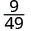
2.
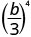
Utilisez la propriété du quotient,\(\left(\dfrac{a}{b}\right)^{m}=\dfrac{a^{m}}{b^{m}}\) 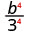
Simplifiez. 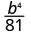
3.

Augmentez le numérateur et le dénominateur à la troisième puissance. 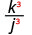
Simplifiez :
- \(\left(\dfrac{5}{8}\right)^{2}\)
- \(\left(\dfrac{p}{10}\right)^{4}\)
- \(\left(\dfrac{m}{n}\right)^{7}\)
- Réponse
-
- \(\dfrac{25}{64}\)
- \(\dfrac{p^{4}}{10,000}\)
- \(\dfrac{m^{7}}{n^{7}}\)
Simplifiez :
- \(\left(\dfrac{1}{3}\right)^{3}\)
- \(\left(\dfrac{-2}{q}\right)^{3}\)
- \(\left(\dfrac{w}{x}\right)^{4}\)
- Réponse
-
- \(\dfrac{1}{27}\)
- \(\dfrac{-8}{q^{3}}\)
- \(\dfrac{w^{4}}{x^{4}}\)
Simplifier les expressions en appliquant plusieurs propriétés
Nous allons maintenant résumer toutes les propriétés des exposants afin qu'elles soient toutes regroupées pour pouvoir être référencées lors de la simplification des expressions à l'aide de plusieurs propriétés. Notez qu'ils sont désormais définis pour les exposants en nombres entiers.
Si a et b sont des nombres réels, et m et n sont des nombres entiers, alors
\[\begin{array}{lrll} \textbf{Product Property} & a^{m} \cdot a^{n} &=&a^{m+n} \\\textbf{Power Property} & \left(a^{m}\right)^{n} &=&a^{m \cdot n} \\\textbf{Product to a Power} & (a b)^{m} &=&a^{m} b^{m} \\ \textbf{Quotient Property} & \dfrac{a^{m}}{a^{n}} &=&a^{m-n}, a \neq 0, m>n \\ & \dfrac{a^{n}}{a^{n}} &=&1, a \neq 0, n>m \\\textbf{Zero Exponent Definition} &a^0&=&1,a\neq 0 \\\textbf{Quotient to a Power Property} & \left(\dfrac{a}{b}\right)^{m} &=&\dfrac{a^{m}}{b^{m}}, b \neq 0 \end{array}\]
Simplifiez :\(\dfrac{\left(y^{4}\right)^{2}}{y^{6}}\)
- Réponse
-
\(\begin{array} {ll} & \dfrac{\left(y^{4}\right)^{2}}{y^{6}} \\ \text{Multiply the exponents in the numerator.} & \dfrac{y^{8}}{y^{6}}\\ \text{Subtract the exponents.} &y^{2} \end{array}\)
Simplifiez :\(\dfrac{\left(m^{5}\right)^{4}}{m^{7}}\)
- Réponse
-
\(m^{13}\)
Simplifiez :\(\dfrac{\left(k^{2}\right)^{6}}{k^{7}}\)
- Réponse
-
\(k^{5}\)
Simplifiez :\(\dfrac{b^{12}}{\left(b^{2}\right)^{6}}\)
- Réponse
-
\[\begin{array} {ll} &\dfrac{b^{12}}{\left(b^{2}\right)^{6}} \\ \text{Multiply the exponents in the numerator.} & \dfrac{b^{12}}{b^{12}}\\ \text{Subtract the exponents.} &b^{0} \\ \text{Simplify} & 1\end{array}\]
Notez qu'après avoir simplifié le dénominateur dans la première étape, le numérateur et le dénominateur étaient égaux. La valeur finale est donc égale à 1.
Simplifiez\(\dfrac{n^{12}}{\left(n^{3}\right)^{4}}\).
- Réponse
-
1
Simplifiez\(\dfrac{x^{15}}{\left(x^{3}\right)^{5}}\).
- Réponse
-
1
Simplifiez :\(\left(\dfrac{y^{9}}{y^{4}}\right)^{2}\)
- Réponse
-
\[\begin{array} {ll} &\left(\dfrac{y^{9}}{y^{4}}\right)^{2}\\ \text{Remember parentheses come before exponents.} &\\ \text{Notice the bases are the same, so we can simplify} &\left(y^{5}\right)^{2} \\ \text{inside the parentheses. Subtract the exponents.} & \\\text{Multiply the exponents.} &y^{10} \end{array}\]
Simplifiez :\(\left(\dfrac{r^{5}}{r^{3}}\right)^{4}\)
- Réponse
-
\(r^{8}\)
Simplifiez :\(\left(\dfrac{v^{6}}{v^{4}}\right)^{3}\)
- Réponse
-
\(v^{6}\)
Simplifiez :\(\left(\dfrac{j^{2}}{k^{3}}\right)^{4}\)
- Réponse
-
Ici, nous ne pouvons pas d'abord simplifier entre parenthèses, car les bases ne sont pas les mêmes.
\(\begin{array} {ll} &\left(\dfrac{j^{2}}{k^{3}}\right)^{4}\\ \text{Raise the numerator and denominator to the third power} & \\ \text{using the Quotient to a Power Property,}\left(\dfrac{a}{b}\right)^{m}=\dfrac{a^{m}}{b^{m}} &\dfrac{\left(j^{2}\right)^{4}}{\left(k^{3}\right)^{4}}\\ \text{Use the Power Property and simplify.} & \dfrac{j^{8}}{k^{12}} \end{array}\)
Simplifiez :\(\left(\dfrac{a^{3}}{b^{2}}\right)^{4}\)
- Réponse
-
\(\dfrac{a^{12}}{b^{8}}\)
Simplifiez :\(\left(\dfrac{q^{7}}{r^{5}}\right)^{3}\)
- Réponse
-
\(\dfrac{q^{21}}{r^{15}}\)
Simplifiez :\(\left(\dfrac{2 m^{2}}{5 n}\right)^{4}\)
- Réponse
-
\(\begin{array} {ll} &\left(\dfrac{2 m^{2}}{5 n}\right)^{4}\\ \text{Raise the numerator and denominator to the fourth} &\dfrac{\left(2 m^{2}\right)^{4}}{(5 n)^{4}} \\ \text{power, using the Quotient to a Power Property,}\left(\dfrac{a}{b}\right)^{m}=\dfrac{a^{m}}{b^{m}} &\dfrac{2^{4}\left(m^{2}\right)^{4}}{5^{4} n^{4}}\\ \text{Use the Power Property and simplify.} & \dfrac{16 m^{8}}{625 n^{4}} \end{array}\)
Simplifiez :\(\left(\dfrac{7 x^{3}}{9 y}\right)^{2}\)
- Réponse
-
\(\dfrac{49 x^{6}}{81 y^{2}}\)
Simplifiez :\(\left(\dfrac{3 x^{4}}{7 y}\right)^{2}\)
- Réponse
-
\(\dfrac{9 x^{8}}{49 v^{2}}\)
Simplifiez :\(\dfrac{\left(x^{3}\right)^{4}\left(x^{2}\right)^{5}}{\left(x^{6}\right)^{5}}\)
- Réponse
-
\(\begin{array}{ll}&\dfrac{\left(x^{3}\right)^{4}\left(x^{2}\right)^{5}}{\left(x^{6}\right)^{5}}\\ \text{Use the Power Property,}\left(a^{m}\right)^{n}=a^{m \cdot n} &\dfrac{\left(x^{12}\right)\left(x^{10}\right)}{\left(x^{30}\right)}\\ \text{Add the exponents in the numerator.} &\dfrac{x^{22}}{x^{30}}\\ \text{Use the Quotient Property,} \dfrac{a^{m}}{a^{n}}=\dfrac{1}{a^{n-m}}&\dfrac{1}{x^{8}}\end{array}\)
Simplifiez :\(\dfrac{\left(a^{2}\right)^{3}\left(a^{2}\right)^{4}}{\left(a^{4}\right)^{5}}\)
- Réponse
-
\(\dfrac{1}{a^{6}}\)
Simplifiez :\(\dfrac{\left(p^{3}\right)^{4}\left(p^{5}\right)^{3}}{\left(p^{7}\right)^{6}}\)
- Réponse
-
\(\dfrac{1}{p^{15}}\)
Simplifiez :\(\dfrac{\left(10 p^{3}\right)^{2}}{(5 p)^{3}\left(2 p^{5}\right)^{4}}\)
- Réponse
-
\(\begin{array} {ll} &\dfrac{\left(10 p^{3}\right)^{2}}{(5 p)^{3}\left(2 p^{5}\right)^{4}}\\ \text { Use the Product to a Power Property, }(a b)^{m}=a^{m} b^{m}&\dfrac{(10)^{2}\left(p^{3}\right)^{2}}{(5)^{3}(p)^{3}(2)^{4}\left(p^{5}\right)^{4}}\\ \text { Use the Power Property, }\left(a^{m}\right)^{n}=a^{m \cdot n}&\dfrac{100 p^{6}}{125 p^{3} \cdot 16 p^{20}}\\ \text { Add the exponents in the denominator. }&\dfrac{100 p^{6}}{125 \cdot 16 p^{23}} \\ \text { Use the Quotient Property, } \dfrac{a^{m}}{a^{n}}=\dfrac{1}{a^{n-m}} & \dfrac{100}{125 \cdot 16 p^{17}} \\ \text { Simplify. } & \dfrac{1}{20 p^{17}} \end{array}\)
Simplifiez :\(\dfrac{\left(3 r^{3}\right)^{2}\left(r^{3}\right)^{7}}{\left(r^{3}\right)^{3}}\)
- Réponse
-
9\(r^{18}\)
Simplifiez :\(\dfrac{\left(2 x^{4}\right)^{5}}{\left(4 x^{3}\right)^{2}\left(x^{3}\right)^{5}}\)
- Réponse
-
\(\dfrac{2}{x}\)
Diviser les monômes
Vous avez maintenant découvert toutes les propriétés des exposants et vous les avez utilisées pour simplifier les expressions. Vous allez maintenant voir comment utiliser ces propriétés pour diviser les monômes. Plus tard, vous les utiliserez pour diviser des polynômes.
Trouvez le quotient :\(56 x^{7} \div 8 x^{3}\)
- Réponse
-
\[\begin{array} {ll} &56 x^{7} \div 8 x^{3}\\ \text { Rewrite as a fraction. }&\dfrac{56 x^{7}}{8 x^{3}}\\ \text { Use fraction multiplication. }&\dfrac{56}{8} \cdot \dfrac{x^{7}}{x^{3}}\\ \text { Simplify and use the Quotient Property. }&7 x^{4}\end{array}\]
Trouvez le quotient :\(42y^{9} \div 6 y^{3}\)
- Réponse
-
\(7y^{6}\)
Trouvez le quotient :\(48z^{8} \div 8 z^{2}\)
- Réponse
-
\(6z^{6}\)
Trouvez le quotient :\(\dfrac{45 a^{2} b^{3}}{-5 a b^{5}}\)
- Réponse
-
Lorsque nous divisons des monômes avec plus d'une variable, nous écrivons une fraction pour chaque variable.
\(\begin{array} {ll} &\dfrac{45 a^{2} b^{3}}{-5 a b^{5}}\\ \text { Use fraction multiplication. }&\dfrac{45}{-5} \cdot \dfrac{a^{2}}{a} \cdot \dfrac{b^{3}}{b^{5}}\\\text { Simplify and use the Quotient Property. }&-9 \cdot a \cdot \dfrac{1}{b^{2}}\\\text { Multiply. }&-\dfrac{9 a}{b^{2}}\end{array}\)
Trouvez le quotient :\(\dfrac{-72 a^{7} b^{3}}{8 a^{12} b^{4}}\)
- Réponse
-
\(-\dfrac{9}{a^{5} b}\)
Trouvez le quotient :\(\dfrac{-63 c^{8} d^{3}}{7 c^{12} d^{2}}\)
- Réponse
-
\(\dfrac{-9 d}{c^{4}}\)
Trouvez le quotient :\(\dfrac{24 a^{5} b^{3}}{48 a b^{4}}\)
- Réponse
-
\(\begin{array} {ll} &\dfrac{24 a^{5} b^{3}}{48 a b^{4}}\\ \text { Use fraction multiplication. }&\dfrac{24}{48} \cdot \dfrac{a^{5}}{a} \cdot \dfrac{b^{3}}{b^{4}}\\\text { Simplify and use the Quotient Property. }&\dfrac{1}{2} \cdot a^{4} \cdot \dfrac{1}{b}\\\text { Multiply. }&\dfrac{a^{4}}{2 b}\end{array}\)
Trouvez le quotient :\(\dfrac{16 a^{7} b^{6}}{24 a b^{8}}\)
- Réponse
-
\(\dfrac{2 a^{6}}{3 b^{2}}\)
Trouvez le quotient :\(\dfrac{27 p^{4} q^{7}}{-45 p^{12} q}\)
- Réponse
-
\(-\dfrac{3 q^{6}}{5 p^{8}}\)
Une fois que vous vous êtes familiarisé avec le processus et que vous l'avez pratiqué étape par étape à plusieurs reprises, vous pourrez peut-être en simplifier une fraction en une seule étape.
Trouvez le quotient :\(\dfrac{14 x^{7} y^{12}}{21 x^{11} y^{6}}\)
- Réponse
-
Veillez à simplifier\(\dfrac{14}{21}\) en divisant un facteur commun et à simplifier les variables en soustrayant leurs exposants.
\(\begin{array} {ll} &\dfrac{14 x^{7} y^{12}}{21 x^{11} y^{6}}\\ \text { Simplify and use the Quotient Property. } & \dfrac{2 y^{6}}{3 x^{4}}\end{array}\)
Trouvez le quotient :\(\dfrac{28 x^{5} y^{14}}{49 x^{9} y^{12}}\)
- Réponse
-
\(\dfrac{4 y^{2}}{7 x^{4}}\)
Trouvez le quotient :\(\dfrac{30 m^{5} n^{11}}{48 m^{10} n^{14}}\)
- Réponse
-
\(\dfrac{5}{8 m^{5} n^{3}}\)
Dans tous les exemples présentés jusqu'à présent, il n'y avait aucun travail à faire sur le numérateur ou le dénominateur avant de simplifier la fraction. Dans l'exemple suivant, nous allons d'abord trouver le produit de deux monômes dans le numérateur avant de simplifier la fraction. Cela suit l'ordre des opérations. N'oubliez pas qu'une barre de fraction est un symbole de regroupement.
Trouvez le quotient :\(\dfrac{\left(6 x^{2} y^{3}\right)\left(5 x^{3} y^{2}\right)}{\left(3 x^{4} y^{5}\right)}\)
- Réponse
-
\(\begin{array} {lc} &\dfrac{\left(6 x^{2} y^{3}\right)\left(5 x^{3} y^{2}\right)}{\left(3 x^{4} y^{5}\right)}\\ \text { Simplify the numerator. }&\dfrac{30 x^{5} y^{5}}{3 x^{4} y^{5}} \\ \text { Simplify. } &10 x \end{array}\)
Trouvez le quotient :\(\dfrac{\left(6 a^{4} b^{5}\right)\left(4 a^{2} b^{5}\right)}{12 a^{5} b^{8}}\)
- Réponse
-
\(2 a b^{2}\)
Trouvez le quotient :\(\dfrac{\left(-12 x^{6} y^{9}\right)\left(-4 x^{5} y^{8}\right)}{-12 x^{10} y^{12}}\)
- Réponse
-
\(-4 x y^{5}\)
Accédez à ces ressources en ligne pour obtenir des instructions et des exercices supplémentaires sur la division des monômes :
- Expressions rationnelles
- Diviser les monômes
- Diviser les monômes 2
Concepts clés
- Propriété du quotient pour les exposants :
- Si a est un nombre réel\(a\neq 0\), et m, n sont des nombres entiers, alors :\(\dfrac{a^{m}}{a^{n}}=a^{m-n}, m>n \text { and } \dfrac{a^{m}}{a^{n}}=\dfrac{1}{a^{m-n}}, n>m\)
- Exposant zéro
- Si a est un nombre différent de zéro, alors\(a^{0} =1\).
- Quotient à une propriété de puissance pour les exposants :
- Si a et b sont des nombres réels et que mm est un nombre de comptage, alors :\(b\neq 0\)\(\left(\dfrac{a}{b}\right)^{m}=\dfrac{a^{m}}{b^{m}}\)
- Pour élever une fraction à une puissance, augmentez le numérateur et le dénominateur à cette puissance.
- Résumé des propriétés des exposants
- Si a, b sont des nombres réels et m, nm, n sont des nombres entiers, alors\(\begin{array}{lrll} \textbf{Product Property} & a^{m} \cdot a^{n} &=&a^{m+n} \\\textbf{Power Property} & \left(a^{m}\right)^{n} &=&a^{m \cdot n} \\\textbf{Product to a Power} & (a b)^{m} &=&a^{m} b^{m} \\ \textbf{Quotient Property} & \dfrac{a^{m}}{a^{n}} &=&a^{m-n}, a \neq 0, m>n \\ & \dfrac{a^{n}}{a^{n}} &=&1, a \neq 0, n>m \\\textbf{Zero Exponent Definition} &a^0&=&1,a\neq 0 \\\textbf{Quotient to a Power Property} & \left(\dfrac{a}{b}\right)^{m} &=&\dfrac{a^{m}}{b^{m}}, b \neq 0 \end{array}\)


