Skip to main content
Global

6.4 : Produits spéciaux

  1. Last updated
  2. Save as PDF
  • Page ID
    195150

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Objectifs d'apprentissage

    À la fin de cette section, vous serez en mesure de :

    • Mettre un binôme au carré en utilisant le motif des carrés binomiaux
    • Multipliez les conjugués en utilisant le modèle Product of Conjugués
    • Reconnaître et utiliser le modèle de produit spécial approprié
    Remarque

    Avant de commencer, répondez à ce questionnaire de préparation.

    Simplifier : a.\(9^2\) b.\((−9)^2\)\(−9^2\) c.

    Si vous avez oublié ce problème, passez en revue l'exercice 1.5.13.

    Mettre un binôme au carré en utilisant le motif des carrés binomiaux

    Les mathématiciens aiment rechercher des modèles qui faciliteront leur travail. La mise au carré des binômes en est un bon exemple. Bien que vous puissiez toujours obtenir le produit en écrivant le binôme deux fois et en utilisant les méthodes de la dernière section, il y a moins de travail à faire si vous apprenez à utiliser un modèle.

    \[\begin{array}{ll}{\text { Let's start by looking at }(x+9)^{2} \text { . }}& \\ {\text { What does this mean? }} &{(x+9)^{2}} \\ {\text { It means to multiply }(x+9) \text { by itself. }} & {(x+9)(x+9)}\\ {\text { Then, using FOIL, we get: }} & {x^{2}+9 x+9 x+81}\\ {\text { Combining like terms gives: }} &{x^{2}+18 x+81} \\ \\ {\text { Here's another one: }} & {(y-7)^{2}} \\ {\text { Multiply }(y-7) \text { by itself. }} & {(y-7)(y-7)} \\ {\text { Using FOIL, we get: }} & {y^{2}-7 y-7 y+49} \\ {\text { And combining like terms: }} & {y^{2}-14 y+49} \\ \\ {\text { And one more: }} & {(2 x+3)^{2}} \\ {\text { Multiply. }} & {(2 x+3)(2 x+3)} \\ {\text { Use FOIL: }} & {\text { 4x }+6 x+6 x+9} \\ {\text { Combine like terms. }} & {4 x^{2}+12 x+9}\end{array} \nonumber\]

    Regardez ces résultats. Voyez-vous des modèles ?

    Qu'en est-il du nombre de termes ? Dans chaque exemple, nous avons quadrillé un binôme et le résultat a été un trinôme.

    \[(a+b)^{2}=\underline{\qquad}+\underline{\qquad}+\underline{\qquad}\nonumber \]

    Maintenant, regardez le premier terme de chaque résultat. D'où vient-il ?

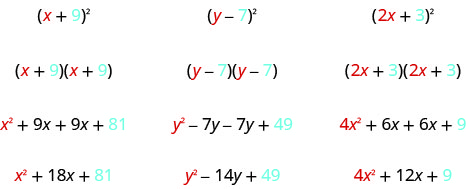
    Cette figure comporte trois colonnes. La première colonne contient l'expression x plus 9, entre parenthèses, au carré. En dessous se trouve le produit de x plus 9 et de x plus 9. En dessous se trouve x au carré plus 9x plus 9x plus 81. En dessous, il y a x au carré plus 18x plus 81. La deuxième colonne contient l'expression y moins 7, entre parenthèses, au carré. En dessous se trouve le produit de y moins 7 et y moins 7. En dessous se trouve y au carré moins 7 ans moins 7 ans plus 49. En dessous se trouve l'expression y au carré moins 14y plus 49. La troisième colonne contient l'expression 2x plus 3, entre parenthèses, au carré. En dessous se trouve le produit de 2x plus 3 et 2x plus 3. En dessous, il y a 4x au carré plus 6x plus 6x plus 9. En dessous, il y a 4x au carré plus 12x plus 9.

    Le premier terme est le produit des premiers termes de chaque binôme. Les binômes étant identiques, il ne s'agit que du carré du premier terme !

    \[(a+b)^{2}=a^{2}+\underline{\qquad}+\underline{\qquad}\nonumber \]

    Pour obtenir le premier terme du produit, mettez le premier terme au carré.

    D'où vient le dernier mandat ? Regardez les exemples et trouvez le modèle.

    Le dernier terme est le produit des derniers termes, qui est le carré du dernier terme.

    \[(a+b)^{2}=\underline{\qquad}+\underline{\qquad}+b^{2}\nonumber \]

    Pour obtenir le dernier terme du produit, mettez le dernier terme au carré.

    Enfin, regardez le moyen terme. Remarquez que cela vient de l'ajout des termes « extérieur » et « intérieur », qui sont tous deux identiques ! Le terme moyen est donc le double du produit des deux termes du binôme.

    \[(a+b)^{2}=\underline{\qquad}+2ab+\underline{\qquad}\nonumber \]

    \[(a+b)^{2}=\underline{\qquad}-2ab+\underline{\qquad}\nonumber \]

    Pour obtenir le terme moyen du produit, multipliez les termes et doublez leur produit.

    Réunir tout cela :

    Motif carré binomial

    Si\(a\) et\(b\) sont des nombres réels, le motif carré binomial est

    \[\underbrace{(a+b)^{2}}_{(\text{binomial})^2} = \underbrace{a^{2}}_{(\text{first term})^2}  +  \underbrace{2 a b}_{2 \times (\text{product of terms})} + \underbrace{a^{2}}_{(\text{last term})^2} \nonumber\]

    Appliquer cela à deux types binomiaux :

    \[\begin{align*} (a+b)^{2} &= a^{2}+2 a b+b^{2} \\[4pt] (a-b)^{2} &=a^{2}- 2 a b + b^{2} \end{align*}\]

    Pour mettre un binôme au carré :

    1. quadriller le premier terme
    2. quadriller le dernier terme
    3. doubler leur produit

    Un exemple numérique permet de vérifier le schéma.

    \(\begin{array}{ll} & {(10+4)^{2}} \\{\text { Square the first term. }}& {10^{2}+\underline{\qquad}+\underline{\qquad}} \\ {\text { Square the last term. }} & {10^{2}+\underline{\qquad}+\frac{1}{4^{2}}} \\ {\text { Double their product. }} & {10^{2}+2 \cdot 10 \cdot 4+4^{2}} \\ {\text { Simplify. }} & {100+80+16} \\ {\text { Simplify. }} & {196}\end{array}\)

    Pour multiplier\((10+4)^2\), vous devez généralement suivre l'ordre des opérations.

    \[\begin{array}{c}{(10+4)^{2}} \\ {(14)^{2}} \\ {196}\end{array}\nonumber \]

    Le patron fonctionne !

    Exemple\(\PageIndex{1}\)

    \(\text { Multiply: }(x+5)^{2}\)

    Solution :

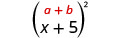      x plus 5, entre parenthèses, au carré. Au-dessus de l'expression se trouve la formule générale a plus b, entre parenthèses, au carré.
    Qualifiez le premier mandat. x au carré, plus le blanc et le blanc. Au-dessus de l'expression se trouve la forme générale a au carré plus 2 a b plus b au carré.
    Qualifier le dernier mandat. x au carré plus 5 au carré.
    Doublez le produit. x au carré plus 2 fois x fois 5 plus 5 au carré. Au-dessus de cette expression se trouve la formule générale a au carré plus 2 fois a fois b plus b au carré.
    Simplifiez. \(x^{2}+10 x+25\)
    Essayez-le ! \(\PageIndex{1}\)

    Multipliez :\((x+9)^{2}\)

    Réponse

    \(x^{2}+18 x+81\)

    Essayez-le ! \(\PageIndex{2}\)

    Multipliez :\((y+11)^{2}\)

    Réponse

    \(y^{2}+22 y+121\)

    Exemple\(\PageIndex{2}\)

    Multipliez :\((y-3)^{2}\)

    Solution :

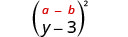      y moins 3, entre parenthèses, au carré. Au-dessus de l'expression se trouve la formule générale a moins b, entre parenthèses, au carré.
    Qualifiez le premier mandat. y au carré moins le blanc et le blanc. Au-dessus de l'expression se trouve la forme générale a au carré plus 2 a b plus b au carré.
    Qualifier le dernier mandat. y au carré moins le blanc plus 3 au carré.
    Doublez le produit. 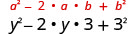y au carré moins y fois y fois 3 plus 3 au carré. Au-dessus de cette expression se trouve la formule générale a au carré plus 2 fois a fois b plus b au carré.
    Simplifiez. \(y^{2}-6 y+9\)
    Essayez-le ! \(\PageIndex{3}\)

    Multipliez :\((x-9)^{2}\)

    Réponse

    \(x^{2}-18 x+81\)

    Essayez-le ! \(\PageIndex{4}\)

    Multipliez :\((p-13)^{2}\)

    Réponse

    \(p^{2}-26 p+169\)

    Exemple\(\PageIndex{3}\)

    Multipliez :\((4 x+6)^{2}\)

    Solution :

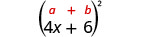      4 x plus 6, entre parenthèses, au carré. Au-dessus de l'expression se trouve la formule générale a plus b, entre parenthèses, au carré.
    Utilise le motif. 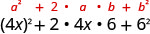4 x au carré plus 2 fois 4 x fois 6 plus 6 au carré. Au-dessus de cette expression se trouve la formule générale a au carré plus 2 fois a fois b plus b au carré.
    Simplifiez. \(16 x^{2}+48 x+36\)
    Essayez-le ! \(\PageIndex{5}\)

    Multipliez :\((6 x+3)^{2}\)

    Réponse

    \(36 x^{2}+36 x+9\)

    Essayez-le ! \(\PageIndex{6}\)

    Multipliez :\((4 x+9)^{2}\)

    Réponse

    \(16 x^{2}+72 x+81\)

    Exemple\(\PageIndex{4}\)

    Multipliez :\((2 x-3 y)^{2}\)

    Solution :

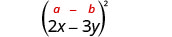      contient 2 x moins 3 y, entre parenthèses, au carré. Au-dessus de l'expression se trouve la formule générale a plus b, entre parenthèses, au carré.
    Utilise le motif. 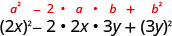2 x au carré moins 2 fois 2 fois 2 fois 3 x fois 3 y plus 3 y au carré. Au-dessus de cette expression se trouve la formule générale a au carré moins 2 fois a fois b plus b au carré.
    Simplifiez. \(4 x^{2}-12 x y+9 y^{2}\)
    Essayez-le ! \(\PageIndex{7}\)

    Multipliez :\((2 c-d)^{2}\)

    Réponse

    \(4 c^{2}-4 c d+d^{2}\)

    Essayez-le ! \(\PageIndex{8}\)

    Multipliez :\((4 x-5 y)^{2}\)

    Réponse

    \(16 x^{2}-40 x y+25 y^{2}\)

    Exemple\(\PageIndex{5}\)

    Multipliez :\(\left(4 u^{3}+1\right)^{2}\)

    Solution :

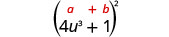      4 u au cube plus 1, entre parenthèses, au carré. Au-dessus de l'expression se trouve la formule générale a plus b, entre parenthèses, au carré.
    Utilise le motif. 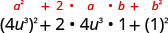4 u en cubes, entre parenthèses, au carré, plus 2 fois 4 u en cubes fois 1 plus 1 au carré. Au-dessus de cette expression se trouve la formule générale a au carré plus 2 fois a fois b plus b au carré.
    Simplifiez. \(16 u^{6}+8 u^{3}+1\)
    Essayez-le ! \(\PageIndex{9}\)

    Multipliez :\(\left(2 x^{2}+1\right)^{2}\)

    Réponse

    \(4 x^{4}+4 x^{2}+1\)

    Essayez-le ! \(\PageIndex{10}\)

    Multipliez :\(\left(3 y^{3}+2\right)^{2}\)

    Réponse

    \(9 y^{6}+12 y^{3}+4\)

    Multipliez les conjugués en utilisant le modèle du produit des conjugués

    Nous venons de voir un modèle de quadrature des binômes que nous pouvons utiliser pour faciliter la multiplication de certains binômes. De même, il existe un modèle pour un autre produit de binômes. Mais avant d'y aller, nous devons introduire du vocabulaire.

    Que remarquez-vous à propos de ces paires de binômes ?

    \[(x-9)(x+9) \qquad(y-8)(y+8)\qquad (2x-5)(2x+5) \nonumber\]

    Regardez le premier terme de chaque binôme dans chaque paire.

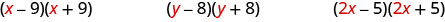
    Cette figurine comporte trois produits. Le premier est x moins 9, entre parenthèses, fois x plus 9, entre parenthèses. La seconde est y moins 8, entre parenthèses, fois y plus 8, entre parenthèses. Le dernier est 2x moins 5, entre parenthèses, fois 2x plus 5, entre parenthèses

    Notez que les premiers termes sont identiques dans chaque paire.

    Examinez les derniers termes de chaque binôme dans chaque paire.

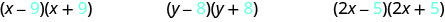
    Cette figurine comporte trois produits. Le premier est x moins 9, entre parenthèses, fois x plus 9, entre parenthèses. La seconde est y moins 8, entre parenthèses, fois y plus 8, entre parenthèses. Le dernier est 2x moins 5, entre parenthèses, fois 2x plus 5, entre parenthèses.

    Notez que les derniers termes sont les mêmes dans chaque paire.

    Remarquez que chaque paire a une somme et une différence.

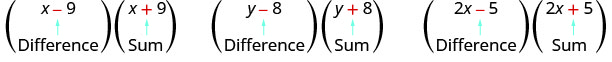
    Cette figurine comporte trois produits. Le premier est x moins 9, entre parenthèses, fois x plus 9, entre parenthèses. Sous le x moins 9 se trouve le mot « différence ». En dessous de x plus 9 se trouve le mot « somme ». La seconde est y moins 8, entre parenthèses, fois y plus 8, entre parenthèses. En dessous de y moins 8 se trouve le mot « différence ». En dessous de y plus 8 se trouve le mot « somme ». Le dernier est 2x moins 5, entre parenthèses, fois 2x plus 5, entre parenthèses. En dessous de 2x moins 5 se trouve le mot « différence » et en dessous de 2x plus 5 se trouve le mot « somme ».

    Une paire de binômes qui ont chacun le même premier terme et le même dernier terme, mais l'un est une somme et l'autre est une différence, porte un nom spécial. Elle est appelée paire conjuguée et se présente sous la forme (a−b), (a+b).

    Définition : paire conjuguée

    Une paire conjuguée est constituée de deux binômes de la forme

    \[(a-b),(a+b)\nonumber \]

    Les deux binômes ont chacun le même premier terme et le même dernier terme, mais l'un des binômes est une somme et l'autre une différence.

    Il existe un bon modèle pour trouver le produit des conjugués. Vous pouvez, bien sûr, simplement FOIL pour obtenir le produit, mais l'utilisation du patron facilite votre travail.

    Cherchons le modèle en utilisant FOIL pour multiplier certaines paires conjuguées.

    \[\begin{array}{cc}{(x-9)(x+9)} & {(y-8)(y+8)} & (2x-5)(2x+5)\\ {x^{2}+9 x-9 x-81} & {y^{2}+8 y-8 y-64} & {4 x^{2}+10 x-10 x-25} \\ {x^{2}-81} & {y^{2}-64} & {4 x^{2}-25}\end{array}\nonumber \]

    Chaque premier terme est le produit des premiers termes des binômes, et comme ils sont identiques, il s'agit du carré du premier terme.

    \[\begin{array}{c}{(a+b)(a-b)=a^{2}-}\underline{\qquad} \\ {\text { To get the}\textbf{ first term, square the first term. }}\end{array}\nonumber \]

    Le dernier terme est obtenu en multipliant les derniers termes, le carré du dernier terme.

    \[\begin{array}{c}{(a+b)(a-b)=a^{2}-b^{2}} \\ {\text { To get the}\textbf{ last term, square the last term. }}\end{array}\nonumber \]

    Qu'observez-vous à propos des produits ?

    Le produit des deux binômes est également un binôme ! La plupart des produits issus du FOIL sont des trinômes.

    Pourquoi n'y a-t-il pas de moyen terme ? Remarquez que les deux termes intermédiaires que vous obtenez avec FOIL se combinent à 0 dans tous les cas, résultat d'une addition et d'une soustraction.

    Le produit des conjugués est toujours de la forme\(a^2-b^2\). C'est ce qu'on appelle une différence de carrés.

    Cela conduit au schéma suivant :

    PRODUIT DU MODÈLE CONJUGATES

    Si\(a\) et\(b\) sont des nombres réels,

    Cette figure est divisée en deux faces. Sur le côté gauche se trouve la formule suivante : le produit de a moins b et de a plus b est égal à un carré moins b au carré. Sur le côté droit se trouve la même formule étiquetée : a moins b et a plus b sont étiquetés « conjugués », le a au carré et le b au carré sont des carrés et le signe moins entre les carrés est intitulé « différence ». Par conséquent, le produit de deux conjugués est appelé différence de carrés.

    Le produit s'appelle une différence de carrés.

    Pour multiplier des conjugués, mettez le premier terme au carré, le dernier terme et écrivez le produit sous la forme d'une différence de carrés.

    Nous allons tester ce modèle à l'aide d'un exemple numérique.

    \(\begin{array}{ll} & (10-2)(10+2)\\ {\text { It is the product of conjugates, so the result will be the }} \\ {\text { difference of two squares. }} & \underline{\qquad} - \underline{\qquad}\\ {\text { Square the first term. }}& 10^2 - \underline{\qquad} \\ {\text { Square the last term. }} & 10^2 - 2^2\\ {\text { Simplify. }} & 100 -4\\ {\text { Simplify. }} & 96\\ {\text { What do you get using the Order of Operations? }} \\ \\ & (10-2)(10+2) \\ & (8)(12) \\ & 96 \end{array}\)

    Remarquez que le résultat est le même !

    Exemple\(\PageIndex{6}\)

    Multipliez :\((x-8)(x+8)\)

    Solution :

    Tout d'abord, reconnaissez qu'il s'agit d'un produit de conjugués. Les binômes ont les mêmes premiers termes et les mêmes derniers termes, et un binôme est une somme et l'autre une différence.

    Cela correspond au motif. 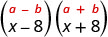Le produit de x moins 8 et x plus 8. Au-dessus se trouve la forme générale a moins b, entre parenthèses, fois a plus b, entre parenthèses.
    Mettre le premier terme au carré, x. 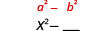x au carré moins le blanc. Au-dessus se trouve la forme générale a au carré moins b au carré.
    Au carré, le dernier mandat, 8. 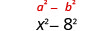x au carré moins 8 au carré.
    Le produit est une différence de carrés. 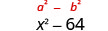x au carré moins 64.
    Essayez-le ! \(\PageIndex{11}\)

    Multipliez :\((x-5)(x+5)\)

    Réponse

    \(x^{2}-25\)

    Essayez-le ! \(\PageIndex{12}\)

    Multipliez :\((w-3)(w+3)\)

    Réponse

    \(w^{2}-9\)

    Exemple\(\PageIndex{7}\)

    Multipliez :\((2 x+5)(2 x-5)\)

    Solution :

    Les binômes sont-ils conjugués ?

    C'est le produit de conjugués. 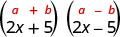Le produit de 2x plus 5 et 2x moins 5. Au-dessus se trouve la forme générale a moins b, entre parenthèses, fois a plus b, entre parenthèses.
    Mettre le premier terme au carré, 2 x 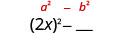2 x carré moins blanc. Au-dessus se trouve la forme générale a au carré moins b au carré.
    Au carré, le dernier terme, 5. 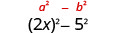2 x au carré moins 5 au carré.
    Simplifiez. Le produit est une différence de carrés. 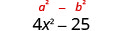4 x au carré moins 25
    Essayez-le ! \(\PageIndex{13}\)

    Multipliez :\((6 x+5)(6 x-5)\)

    Réponse

    \(36 x^{2}-25\)

    Essayez-le ! \(\PageIndex{14}\)

    Multipliez :\((2 x+7)(2 x-7)\)

    Réponse

    \(4 x^{2}-49\)

    Les binômes de l'exemple suivant peuvent regarder en arrière ; la variable se trouve dans le second terme. Mais les deux binômes sont toujours conjugués, nous utilisons donc le même modèle pour les multiplier.

    Exemple\(\PageIndex{8}\)

    Trouvez le produit :\((3+5 x)(3-5 x)\)

    Solution :

    C'est le produit de conjugués. 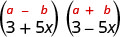Le produit de 3 plus 5 x et 3 moins 5 x. Au-dessus se trouve la forme générale a plus b, entre parenthèses, fois a moins b, entre parenthèses.
    Utilise le motif. 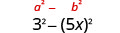3 au carré moins 5 x au carré. Au-dessus se trouve la forme générale a au carré moins b au carré.
    Simplifiez. \(9-25 x^{2}\)
    Essayez-le ! \(\PageIndex{15}\)

    Multipliez :\((7+4 x)(7-4 x)\)

    Réponse

    \(49-16 x^{2}\)

    Essayez-le ! \(\PageIndex{16}\)

    Multipliez :\((9-2 y)(9+2 y)\)

    Réponse

    \(81-4 y^{2}\)

    Nous allons maintenant multiplier les conjugués qui ont deux variables.

    Exemple\(\PageIndex{9}\)

    Trouvez le produit :\((5 m-9 n)(5 m+9 n)\)

    Solution :

    Cela correspond au modèle. 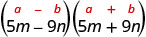5 m moins 9 n et 5 m plus 9 n. Au-dessus se trouve la forme générale a plus b, entre parenthèses, fois a moins b, entre parenthèses.
    Utilise le motif. 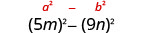5 mm au carré moins 9 m au carré. Au-dessus se trouve la forme générale a au carré moins b au carré.
    Simplifiez. \(25 m^{2}-81 n^{2}\)
    Essayez-le ! \(\PageIndex{17}\)

    Trouvez le produit :\((4 p-7 q)(4 p+7 q)\)

    Réponse

    \(16 p^{2}-49 q^{2}\)

    Essayez-le ! \(\PageIndex{18}\)

    Trouvez le produit :\((3 x-y)(3 x+y)\)

    Réponse

    \(9 x^{2}-y^{2}\)

    Exemple\(\PageIndex{10}\)

    Trouvez le produit :\((c d-8)(c d+8)\)

    Solution :

    Cela correspond au modèle. 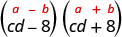Le produit de c d moins 8 et de c d plus 8. Au-dessus se trouve la forme générale a plus b, entre parenthèses, fois a moins b, entre parenthèses.
    Utilise le motif. 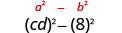c d au carré moins 8 au carré. Au-dessus se trouve la forme générale a au carré moins b au carré.
    Simplifiez. \(c^{2} d^{2}-64\)
    Essayez-le ! \(\PageIndex{19}\)

    Trouvez le produit :\((x y-6)(x y+6)\)

    Réponse

    \(x^{2} y^{2}-36\)

    Essayez-le ! \(\PageIndex{20}\)

    Trouvez le produit :\((a b-9)(a b+9)\)

    Réponse

    \(a^{2} b^{2}-81\)

    Exemple\(\PageIndex{11}\)

    Trouvez le produit :\(\left(6 u^{2}-11 v^{5}\right)\left(6 u^{2}+11 v^{5}\right)\)

    Solution :

    Cela correspond au modèle. 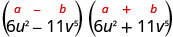Le produit de 6 u au carré moins 11 v à la cinquième puissance et de 6 u au carré plus 11 v à la cinquième puissance. Au-dessus se trouve la forme générale a plus b, entre parenthèses, fois a moins b, entre parenthèses.
    Utilise le motif. 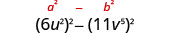6 u au carré, entre parenthèses, au carré, moins 11 v jusqu'à la cinquième puissance, entre parenthèses, au carré. Au-dessus se trouve la forme générale a au carré moins b au carré.
    Simplifiez. \(36 u^{4}-121 v^{10}\)
    Essayez-le ! \(\PageIndex{21}\)

    Trouvez le produit :\(\left(3 x^{2}-4 y^{3}\right)\left(3 x^{2}+4 y^{3}\right)\)

    Réponse

    \(9 x^{4}-16 y^{6}\)

    Essayez-le ! \(\PageIndex{22}\)

    Trouvez le produit :\(\left(2 m^{2}-5 n^{3}\right)\left(2 m^{2}+5 n^{3}\right)\)

    Réponse

    \(4 m^{4}-25 n^{6}\)

    Reconnaître et utiliser le modèle de produit spécial approprié

    Nous venons de développer des modèles de produits spéciaux pour les carrés binomiaux et pour le produit des conjugués. Les produits se ressemblent, il est donc important de savoir quand il est approprié d'utiliser chacun de ces modèles et de remarquer en quoi ils diffèrent. Examinez les deux modèles ensemble et notez leurs similitudes et leurs différences.

    COMPARAISON DES MODÈLES DE PRODUITS SPÉCIAUX

    \(\begin{array}{ll }{\textbf { Binomial Squares }}&{\textbf { Product of Conjugates }} \\ {(a+b)^{2}=a^{2}+2 a b+b^{2}} & {(a-b)(a+b)=a^{2}-b^{2}} \\ {(a-b)^{2}=a^{2}+2 a b+b^{2}} \\ {\text { - Squaring a binomial }}& {\text { - Multiplying conjugates }} \\ {\text { - Product is a trinomial }} & {\text { - Product is a binomial }} \\ {\text { - Inner and outer terms with FOIL are the same. }} &{\text { - Inner and outer terms with FOIL are opposites. }} \\ {\text { - Middle term is double the product of the terms. }} &{\text { - There is no middle term. }} \end{array}\)

    Exemple\(\PageIndex{12}\)

    Choisissez le motif approprié et utilisez-le pour trouver le produit :

    1. \((2 x-3)(2 x+3)\)
    2. \((8 x-5)^{2}\)
    3. \((6 m+7)^{2}\)
    4. \((5 x-6)(6 x+5)\)

    Solution :

    1. \((2x−3)(2x+3)\)Ce sont des conjugués. Ils ont les mêmes premiers nombres et les mêmes derniers chiffres, et un binôme est une somme et l'autre une différence. Il correspond au modèle Product of Conjugués.

    Cela correspond au modèle. 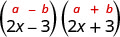Le produit de 2 x moins 3 et 2 x plus 3. Au-dessus se trouve la forme générale a plus b, entre parenthèses, fois a moins b, entre parenthèses.
    Utilise le motif. 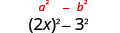2 x au carré moins 3 au carré. Au-dessus se trouve la forme générale a au carré moins b au carré.
    Simplifiez. \(4 x^{2}-9\)

    2. \((8 x-5)^{2}\)On nous demande de quadriller un binôme. Il s'adapte au motif des carrés binomiaux.

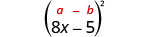      8 x moins 5, entre parenthèses, au carré. Au-dessus se trouve la forme générale a moins b, entre parenthèses, au carré.
    Utilise le motif. 8 x au carré moins 2 fois 8 x fois 5 plus 5 au carré. Au-dessus se trouve la forme générale a au carré moins 2 a b plus b au carré.
    Simplifiez. \(64 x^{2}-80 x+25\)

    3. \((6 m+7)^{2}\)Encore une fois, nous allons mettre un binôme au carré, donc nous utilisons le modèle des carrés binomiaux.

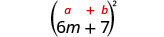      6 m plus 7, entre parenthèses, au carré. Au-dessus se trouve la forme générale a plus b, entre parenthèses, au carré.
    Utilise le motif. 6 m au carré plus 2 fois 6 m fois 7 plus 7 au carré. Au-dessus se trouve la forme générale a au carré plus 2 a b plus b au carré.
    Simplifiez. \(36 m^{2}+84 m+49\)

    4. \((5 x-6)(6 x+5)\)Ce produit ne correspond pas aux motifs, nous utiliserons donc du FOIL.

    \(\begin{array}{ll} & (5 x-6)(6 x+5)\\ {\text { Use FOIL. }} & {30 x^{2}+25 x-36 x-30} \\ {\text { Simplify. }} & {30 x^{2}-11 x-30}\end{array}\)

    Essayez-le ! \(\PageIndex{23}\)

    Choisissez le motif approprié et utilisez-le pour trouver le produit :

    1. \((9b−2)(2b+9)\)
    2. \((9p−4)2\)
    3. \((7y+1)^2\)
    4. \((4r-3)(4r+3)\)
    Réponse
    1. DÉJOUER ;\(18 b^{2}+77 b-18\)
    2. Carrés binomiaux ;\(81 p^{2}-72 p+16\)
    3. Carrés binomiaux ;\(49 y^{2}+14 y+1\)
    4. Produit à base de conjugués ;\(16 r^{2}-9\)
    Essayez-le ! \(\PageIndex{24}\)

    Choisissez le motif approprié et utilisez-le pour trouver le produit :

    1. \((6x+7)^2\)
    2. \((3x−4)(3x+4)\)
    3. \((2x−5)(5x−2)\)
    4. \((6n−1)^2\)
    Réponse
    1. Carrés binomiaux ;\(36 x^{2}+84 x+49\)
    2. Produit à base de conjugués ;\(9 x^{2}-16\)
    3. DÉJOUER ;\(10 x^{2}-29 x+10\)
    4. Carrés binomiaux ;\(36 n^{2}-12 n+1\)
    Remarque

    Accédez à ces ressources en ligne pour obtenir des instructions et des exercices supplémentaires avec des produits spéciaux :

    • Produits spéciaux

    Concepts clés

    • Motif de carrés binomiaux
      • Si a, b sont des nombres réels,
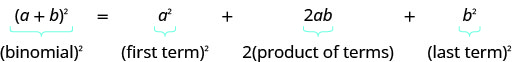
        Pas de texte alternatif
      • \((a+b)^{2}=a^{2}+2 a b+b^{2}\)
      • \((a-b)^{2}=a^{2}-2 a b+b^{2}\)
      • Pour mettre un binôme au carré : mettre au carré le premier terme, mettre le dernier terme au carré, doubler leur produit.
    • Produit de Conjugates Pattern
      • Si a, ba, b sont des nombres réels,
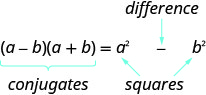
        Pas de texte alternatif
      • \((a-b)(a+b)=a^{2}-b^{2}\)
      • Le produit s'appelle une différence de carrés.
    • Pour multiplier les conjugués :
      • carré le premier terme carré le dernier terme écrivez-le comme une différence de carrés

    Lexique

    paire conjuguée
    Une paire conjuguée est constituée de deux binômes de la forme\((a−b)\) et\((a+b)\) ; les deux binômes ont chacun le même premier terme et le même dernier terme, mais l'un des binômes est une somme et l'autre une différence.