6.3E : Exercices
- Page ID
- 195127
La pratique rend la perfection
Multiplier un polynôme par un monomial
Dans les exercices suivants, multipliez.
4\((w+10)\)
- Réponse
-
4 w+40
6 (b+8)
−3 (a+7)
- Réponse
-
−3a−21
−5 (p+9)
2 (x−7)
- Réponse
-
2x−14
7 (y−4)
−3 (k−4)
- Réponse
-
−3 k+12
−8 (j−5)
q (q+5)
- Réponse
-
\(q^{2}+5 q\)
k (k+7)
−b (b+9)
- Réponse
-
\(-b^{2}-9 b\)
−y (y+3)
−x (x−10)
- Réponse
-
\(-x^{2}+10 x\)
−p (p−15)
6r (4r+s)
- Réponse
-
\(24 r^{2}+6 r s\)
5 cm (9 c+D)
12 fois (x−10)
- Réponse
-
\(12 x^{2}-120 x\)
9 m (m−11)
−9a (3a+5)
- Réponse
-
\(-27 a^{2}-45 a\)
−4p (2p+7)
3\(\left(p^{2}+10 p+25\right)\)
- Réponse
-
\(3 p^{2}+30 p+75\)
6\(\left(y^{2}+8 y+16\right)\)
\(-8 x\left(x^{2}+2 x-15\right)\)
- Réponse
-
\(-8 x^{3}-16 x^{2}+120 x\)
\(-5 t\left(t^{2}+3 t-18\right)\)
5\(q^{3}\left(q^{3}-2 q+6\right)\)
- Réponse
-
\(5 q^{6}-10 q^{4}+30 q^{3}\)
4\(x^{3}\left(x^{4}-3 x+7\right)\)
\(-8 y\left(y^{2}+2 y-15\right)\)
- Réponse
-
\(-8 y^{3}-16 y^{2}+120 y\)
\(-5 m\left(m^{2}+3 m-18\right)\)
5\(q^{3}\left(q^{2}-2 q+6\right)\)
- Réponse
-
\(5 q^{5}-10 q^{4}+30 q^{3}\)
9\(r^{3}\left(r^{2}-3 r+5\right)\)
\(-4 z^{2}\left(3 z^{2}+12 z-1\right)\)
- Réponse
-
\(-12 z^{4}-48 z^{3}+4 z^{2}\)
\(-3 x^{2}\left(7 x^{2}+10 x-1\right)\)
\((2 m-9) m\)
- Réponse
-
\(2 m^{2}-9 m\)
\((8 j-1) j\)
\((w-6) \cdot 8\)
- Réponse
-
\(8 w-48\)
\((k-4) \cdot 5\)
4\((x+10)\)
- Réponse
-
4 x 40
6 (a+8)
15 (r−24)
- Réponse
-
15r−360
12 (v−30)
−3 (m+11)
- Réponse
-
−3 m−33
−4 (p+15)
−8 (z−5)
- Réponse
-
−8 z+40
−3 (x−9)
u (u+5)
- Réponse
-
\(u^{2}+5 u\)
\(q(q+7)\)
\(n\left(n^{2}-3 n\right)\)
- Réponse
-
\(n^{3}-3 n^{2}\)
\(s\left(s^{2}-6 s\right)\)
6\(x(4 x+y)\)
- Réponse
-
\(24 x^{2}+6 x y\)
5a (9a+b)
5 p (11 p−5 q)
- Réponse
-
\(55 p^{2}-25 p q\)
12\(u(3 u-4 v)\)
3\(\left(v^{2}+10 v+25\right)\)
- Réponse
-
\(3 v^{2}+30 v+75\)
6\(\left(x^{2}+8 x+16\right)\)
2\(n\left(4 n^{2}-4 n+1\right)\)
- Réponse
-
\(8 n^{3}-8 n^{2}+2 n\)
3\(r\left(2 r^{2}-6 r+2\right)\)
\(-8 y\left(y^{2}+2 y-15\right)\)
- Réponse
-
\(-8 y^{3}-16 y^{2}+120 y\)
\(-5 m\left(m^{2}+3 m-18\right)\)
5\(q^{3}\left(q^{2}-2 q+6\right)\)
- Réponse
-
\(5 q^{5}-10 q^{4}+30 q^{3}\)
9\(r^{3}\left(r^{2}-3 r+5\right)\)
\(-4 z^{2}\left(3 z^{2}+12 z-1\right)\)
- Réponse
-
\(-12 z^{4}-48 z^{3}+4 z^{2}\)
\(-3 x^{2}\left(7 x^{2}+10 x-1\right)\)
\((2 y-9) y\)
- Réponse
-
\(18 y^{2}-9 y\)
\((8 b-1) b\)
Multipliez un binôme par un binôme
Dans les exercices suivants, multipliez les binômes suivants en utilisant : ⓐ la propriété distributive ⓑ la méthode FOIL ⓒ la méthode verticale.
(w+5) (w+7)
- Réponse
-
\(w^{2}+12 w+35\)
(y+9) (y+3)
(p+11) (p−4)
- Réponse
-
\(p^{2}+7 p-44\)
(q+4) (q−8)
Dans les exercices suivants, multipliez les binômes. Utilisez n'importe quelle méthode.
(x+8) (x+3)
- Réponse
-
\(x^{2}+11 x+24\)
(y+7) (y+4)
(y−6) (y−2)
- Réponse
-
\(y^{2}-8 y+12\)
(x−7) (x−2)
(w−4) (w+7)
- Réponse
-
\(w^{2}+3 w-28\)
\((q-5)(q+8)\)
(p+12) (p−5)
- Réponse
-
\(p^{2}+7 p-60\)
(m+11) (m−4)
(6p+5) (p+1)
- Réponse
-
\(6 p^{2}+11 p+5\)
\((7 m+1)(m+3)\)
(2t−9) (10t+1)
- Réponse
-
\(20 t^{2}-88 t-9\)
(3r−8) (11r+1)
(5 x y) (3 x − 6)
- Réponse
-
\(15 x^{2}-3 x y-30 x+6 y\)
(10a−b) (3a−4)
(a+b) (2a+3b)
- Réponse
-
\(2 a^{2}+5 a b+3 b^{2}\)
(r+s) (3r+2)
(4z−y) (z−6)
- Réponse
-
\(4 z^{2}-24 z-z y+6 y\)
(5x−y) (x−4)
\(\left(x^{2}+3\right)(x+2)\)
- Réponse
-
\(x^{3}+2 x^{2}+3 x+6\)
\(\left(y^{2}-4\right)(y+3)\)
\(\left(x^{2}+8\right)\left(x^{2}-5\right)\)
- Réponse
-
\(x^{4}+3 x^{2}-40\)
\(\left(y^{2}-7\right)\left(y^{2}-4\right)\)
(5 ab−1) (2 ab+3)
- Réponse
-
\(10 a^{2} b^{2}+13 a b-3\)
(2 xy+3) (3 xy+2)
(6 personnes − 3) (4 personnes − 5)
- Réponse
-
\(24 p^{2} q^{2}-42 p q+15\)
(3rs−7) (3rs−4)
Multipliez un trinôme par un binôme
Dans les exercices suivants, multipliez en utilisant ⓐ la propriété distributive ⓑ la méthode verticale.
\((x+5)\left(x^{2}+4 x+3\right)\)
- Réponse
-
\(x^{3}+9 x^{2}+23 x+15\)
\((u+4)\left(u^{2}+3 u+2\right)\)
\((y+8)\left(4 y^{2}+y-7\right)\)
- Réponse
-
\(4 y^{3}+33 y^{2}+y-56\)
\((a+10)\left(3 a^{2}+a-5\right)\)
Dans les exercices suivants, multipliez. Utilisez l'une des deux méthodes.
\((w-7)\left(w^{2}-9 w+10\right)\)
- Réponse
-
\(w^{3}-16 w^{2}+73 w-70\)
\((p-4)\left(p^{2}-6 p+9\right)\)
\((3 q+1)\left(q^{2}-4 q-5\right)\)
- Réponse
-
\(3 q^{3}-11 q^{2}-19 q-5\)
\((6 r+1)\left(r^{2}-7 r-9\right)\)
Pratique mixte
(10 ans − 6 ans) + (4 ans − 7 ans)
- Réponse
-
14 ans et 13 ans
(15 p−4) + (3 p−5)
\(\left(x^{2}-4 x-34\right)-\left(x^{2}+7 x-6\right)\)
- Réponse
-
−11 x −28
\(\left(j^{2}-8 j-27\right)-\left(j^{2}+2 j-12\right)\)
5\(q\left(3 q^{2}-6 q+11\right)\)
- Réponse
-
\(15 q^{3}-30 q^{2}+55 q\)
8\(t\left(2 t^{2}-5 t+6\right)\)
(s−7) (+9)
- Réponse
-
\(s^{2}+2 s-63\)
(x−5) (x+13)
\(\left(y^{2}-2 y\right)(y+1)\)
- Réponse
-
\(y^{3}-y^{2}-2 y\)
\(\left(a^{2}-3 a\right)(4 a+5)\)
\((3 n-4)\left(n^{2}+n-7\right)\)
- Réponse
-
\(3 n^{3}-n^{2}-25 n+28\)
\((6 k-1)\left(k^{2}+2 k-4\right)\)
\((7 p+10)(7 p-10)\)
- Réponse
-
\(49 p^{2}-100\)
(3 ans+8) (3 ans − 8)
\(\left(4 m^{2}-3 m-7\right) m^{2}\)
- Réponse
-
\(4 m^{4}-3 m^{3}-7 m^{2}\)
\(\left(15 c^{2}-4 c+5\right) c^{4}\)
\((5 a+7 b)(5 a+7 b)\)
- Réponse
-
\(25 a^{2}+70 a b+49 b^{2}\)
(3x−11 ans) (3x−11 ans)
(4 ans+12 z) (4 à 12 z)
- Réponse
-
\(16 y^{2}-144 z^{2}\)
Mathématiques quotidiennes
Mathématiques mentales Vous pouvez utiliser la multiplication binomiale pour multiplier des nombres sans calculatrice. Supposons que vous deviez multiplier 13 fois 15. Considérez 13 comme 10+3 et 15 comme 10+5.
- Multipliez (10+3) (10+5) par la méthode FOIL.
- Multipliez 13·15 sans utiliser de calculatrice.
- Quel est le moyen le plus simple pour toi ? Pourquoi ?
Mathématiques mentales Vous pouvez utiliser la multiplication binomiale pour multiplier des nombres sans calculatrice. Supposons que vous deviez multiplier 18 fois 17. Considérez 18 comme 20−2 et 17 comme 20−3.
- Multipliez (20−2) (20−3) par la méthode FOIL.
- Multipliez 18·17 sans utiliser de calculatrice.
- Quel est le moyen le plus simple pour toi ? Pourquoi ?
- Réponse
-
- 306
- 306
- Les réponses peuvent varier.
Exercices d'écriture
Quelle méthode préférez-vous utiliser pour multiplier deux binômes : la propriété distributive, la méthode FOIL ou la méthode verticale ? Pourquoi ?
Quelle méthode préférez-vous utiliser pour multiplier un trinôme par un binôme : la propriété distributive ou la méthode verticale ? Pourquoi ?
- Réponse
-
Les réponses peuvent varier.
Multipliez ce qui suit :
\(\begin{array}{l}{(x+2)(x-2)} \\ {(y+7)(y-7)} \\ {(w+5)(w-5)}\end{array}\)
Expliquez le schéma que vous voyez dans vos réponses.
Multipliez ce qui suit :
\(\begin{array}{l}{(m-3)(m+3)} \\ {(n-10)(n+10)} \\ {(p-8)(p+8)}\end{array}\)
Expliquez le schéma que vous voyez dans vos réponses.
- Réponse
-
Les réponses peuvent varier.
Multipliez ce qui suit :
\(\begin{array}{l}{(p+3)(p+3)} \\ {(q+6)(q+6)} \\ {(r+1)(r+1)}\end{array}\)
Expliquez le schéma que vous voyez dans vos réponses.
Multipliez ce qui suit :
\(\begin{array}{l}{(x-4)(x-4)} \\ {(y-1)(y-1)} \\ {(z-7)(z-7)}\end{array}\)
Expliquez le schéma que vous voyez dans vos réponses.
- Réponse
-
Les réponses peuvent varier.
Auto-vérification
a. Une fois les exercices terminés, utilisez cette liste de contrôle pour évaluer votre maîtrise des objectifs de cette section.
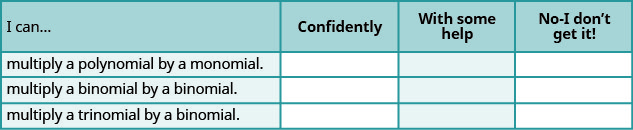
b. Que vous indique cette liste de contrôle sur votre maîtrise de cette section ? Quelles mesures allez-vous prendre pour vous améliorer ?


