Skip to main content
Global

6.3 : Multiplier les polynômes

  1. Last updated
  2. Save as PDF
  • Page ID
    195103

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Objectifs d'apprentissage

    À la fin de cette section, vous serez en mesure de :

    • Multipliez un polynôme par un monomial
    • Multipliez un binôme par un binôme
    • Multipliez un trinôme par un binôme
    Remarque

    Avant de commencer, répondez à ce questionnaire de préparation.

    1. Distribuez :\(2(x+3)\).
      Si vous avez oublié ce problème, passez en revue l'exercice 1.10.31.
    2. Combinez des termes similaires :\(x^{2}+9x+7x+63\).
      Si vous avez oublié ce problème, passez en revue l'exercice 1.3.37.

    Multiplier un polynôme par un monomial

    Nous avons utilisé la propriété distributive pour simplifier des expressions telles que\(2(x−3)\). Vous avez multiplié les deux termes entre parenthèses\(x\) et\(3\), par\(2\), pour obtenir\(2x−6\). Avec le nouveau vocabulaire de ce chapitre, vous pouvez dire que vous multipliez un binôme par un monomial\(2\).\(x−3\)

    Multiplier un binôme par un monomial n'a rien de nouveau pour vous ! Voici un exemple :

    Exercice\(\PageIndex{1}\)

    Multipliez :\(4(x+3)\).

    Réponse
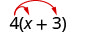
      4 fois x plus 3. Deux flèches partent de 4 et se terminent par x et 3.
    Distribuez. \(4 \cdot x+4 \cdot 3\)
    Simplifiez. \(4 x+12\)
    Exercice\(\PageIndex{2}\)

    Multipliez :\(5(x+7)\).

    Réponse

    5 x 35

    Exercice\(\PageIndex{3}\)

    Multipliez :\(3(y+13)\).

    Réponse

    3 ans+39

    Exercice\(\PageIndex{4}\)

    Multipliez : y (y−2).

    Réponse
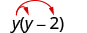
      Y fois y moins 2. Deux flèches partent du coefficient y et se terminent par y et moins 2 entre parenthèses.
    Distribuez. \(y \cdot y-y \cdot 2\)
    Simplifiez. \(y^{2}-2 y\)
    Exercice\(\PageIndex{5}\)

    Multipliez :\(x(x−7)\).

    Réponse

    \(x^{2}-7 x\)

    Exercice\(\PageIndex{6}\)

    Multipliez :\(d(d−11)\).

    Réponse

    \(d^{2}-11d\)

    Exercice\(\PageIndex{7}\)

    Multipliez :\(7x(2 x+y)\)

    Réponse
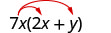
      7 x fois 2 x plus y. Deux flèches partent de 7x et se terminent par 2x et y.
    Distribuez. 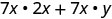7 fois 2 x plus 7 fois y.
    Simplifiez. 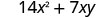14 x au carré plus 7 x y.
    Exercice\(\PageIndex{8}\)

    Multipliez :\(5x(x+4 y)\)

    Réponse

    \(5 x^{2}+20 x y\)

    Exercice\(\PageIndex{9}\)

    Multipliez :\(2p(6 p+r)\)

    Réponse

    \(12 p^{2}+2 p r\)

    Exercice\(\PageIndex{10}\)

    Multipliez :\(-2 y\left(4 y^{2}+3 y-5\right)\)

    Réponse
      Négatif 2 y fois 4 y au carré plus 3 y moins 5. Trois flèches partent de moins 2 y et se terminent par 4 y au carré, 3 y et moins 5.
    Distribuez. 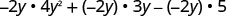Négatif 2 y fois 4 y au carré plus moins 2 y fois 3 y moins moins 2 y fois 5.
    Simplifiez. 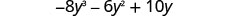Négatif : 8 g en cubes moins 6 g au carré plus 10 g.
    Exercice\(\PageIndex{11}\)

    Multipliez :\(-3 y\left(5 y^{2}+8 y-7\right)\)

    Réponse

    \(-15 y^{3}-24 y^{2}+21 y\)

    Exercice\(\PageIndex{12}\)

    Multipliez :\(4x^{2}\left(2 x^{2}-3 x+5\right)\)

    Réponse

    \(8 x^{4}-24 x^{3}+20 x^{2}\)

    Exercice\(\PageIndex{13}\)

    Multipliez :\(2x^{3}\left(x^{2}-8 x+1\right)\)

    Réponse
      2 fois en cubes x au carré moins 8 x plus 1. Trois flèches partent de 2 x cubes et se terminent par x au carré, moins 8 x et 1.
    Distribuez. \(2 x^{3} \cdot x^{2}+\left(2 x^{3}\right) \cdot(-8 x)+\left(2 x^{3}\right) \cdot 1\)
    Simplifiez. \(2 x^{5}-16 x^{4}+2 x^{3}\)
    Exercice\(\PageIndex{14}\)

    Multipliez : 4\(x\left(3 x^{2}-5 x+3\right)\)

    Réponse

    \(12 x^{3}-20 x^{2}+12 x\)

    Exercice\(\PageIndex{15}\)

    Multipliez :\(-6 a^{3}\left(3 a^{2}-2 a+6\right)\)

    Réponse

    \(-18 a^{5}+12 a^{4}-36 a^{3}\)

    Exercice\(\PageIndex{16}\)

    Multipliez :\((x+3) p\)

    Réponse
    Le monomial est le second facteur. x plus 3, entre parenthèses, fois p. Deux flèches partent du p et se terminent en x et 3.
    Distribuez. \(x \cdot p+3 \cdot p\)
    Simplifiez. \ (\ x p+3 p)
    Exercice\(\PageIndex{17}\)

    Multipliez :\((x+8) p\)

    Réponse

    \(x p+8 p\)

    Exercice\(\PageIndex{18}\)

    Multipliez :\((a+4) p\)

    Réponse

    \(a p+4 p\)

    Multipliez un binôme par un binôme

    Tout comme il existe différentes manières de représenter la multiplication de nombres, il existe plusieurs méthodes qui peuvent être utilisées pour multiplier un binôme par un binôme. Nous allons commencer par utiliser la propriété distributive.

    Multipliez un binôme par un binôme en utilisant la propriété distributive

    Regardez Exercice\(\PageIndex{16}\), où nous avons multiplié un binôme par un monomial.

    Instructions Expression
    Expressions de départ x plus 3, entre parenthèses, fois p. Deux flèches partent du p et se terminent en x et 3.
    Nous l'avons distribué\(p\) pour obtenir : 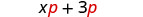x p plus 3 p.
    Et si on l'avait fait à la\((x + 7)\) place de\(p\) ? x plus 3 multiplié par x plus 7. Deux flèches partent de x plus 7 et se terminent au x et au 3 dans le premier binôme.
    Distribuez\((x + 7)\). 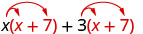La somme de deux produits. Le produit de x et x plus 7, plus le produit de 3 et x plus 7.
    Distribuez à nouveau. \(x^{2}+7 x+3 x+21\)
    Combinez les mêmes termes. \(x^{2}+10 x+21\)

    Notez qu'avant de combiner des termes similaires, vous aviez quatre termes. Vous avez multiplié les deux termes du premier binôme par les deux termes du second binôme, soit quatre multiplications.

    Exercice\(\PageIndex{19}\)

    Multipliez :\((y+5)(y+8)\)

    Réponse
      Le produit de deux binômes, y plus 5 et y plus 8. Deux flèches partent de y plus 8 et se terminent par le y et le 5 dans le premier binôme.
    Répartir (y + 8). 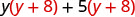Somme de deux produits, le produit de y et y plus 8, plus le produit de 5 et de y plus 8.
    Distribuez à nouveau \(y^{2}+8 y+5 y+40\)
    Combinez les mêmes termes. \ (\ y^ {2} +13 y+40)
    Exercice\(\PageIndex{20}\)

    Multipliez :\((x+8)(x+9)\)

    Réponse

    \(x^{2}+17 x+72\)

    Exercice\(\PageIndex{21}\)

    Multipliez :\((5 x+9)(4 x+3)\)

    Réponse

    \(20 x^{2}+51 x+27\)

    Exercice\(\PageIndex{22}\)

    Multipliez :\((2 y+5)(3 y+4)\)

    Réponse
      Le produit de deux binômes, 2 y plus 5 et 3 y plus 4. Deux flèches partent de 3y plus 4 et se terminent à 2y et 5 dans le premier binôme.
    Répartir (3 y + 4). 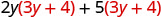Somme de deux produits, le produit de 2 y et 3 y plus 4, plus le produit de 5 et 3 y plus 4.
    Distribuez à nouveau \(6 y^{2}+8 y+15 y+20\)
    Combinez les mêmes termes. \(6 y^{2}+23 y+20\)
    Exercice\(\PageIndex{23}\)

    Multipliez :\((3 b+5)(4 b+6)\)

    Réponse

    \(12 b^{2}+38 b+30\)

    Exercice\(\PageIndex{24}\)

    Multipliez :\((a+10)(a+7)\)

    Réponse

    \(a^{2}+17 a+70\)

    Exercice\(\PageIndex{25}\)

    Multipliez :\((4 y+3)(2 y-5)\)

    Réponse
      Exemple 6.36.jpg
    Distribuer. 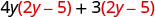La somme de deux produits, le produit de 4y et 2y moins 5, plus le produit de 3 et 2y moins 5.
    Distribuez à nouveau. \(8 y^{2}-20 y+6 y-15\)
    Combinez les mêmes termes. \(8 y^{2}-14 y-15\)
    Exercice\(\PageIndex{26}\)

    Multipliez :\((5 y+2)(6 y-3)\)

    Réponse

    \(30 y^{2}-3 y-6\)

    Exercice\(\PageIndex{27}\)

    Multipliez :\((3 c+4)(5 c-2)\)

    Réponse

    \(15 c^{2}+14 c-8\)

    Exercice\(\PageIndex{28}\)

    Multipliez :\((x-2)(x-y)\)

    Réponse
      Produit de deux binômes, x moins 2 et x moins y. Deux flèches partent de x moins y et se terminent par x et 2 dans le premier binôme.
    Distribuer. La différence entre deux produits. Le produit de x et x moins 7, moins le produit de 2 et x moins y.
    Distribuez à nouveau. \(x^{2}-x y-2 x+2 y\)
    Il n'y a pas de termes similaires à combiner.  
    Exercice\(\PageIndex{29}\)

    Multipliez :\((a+7)(a-b)\)

    Réponse

    \(a^{2}-a b+7 a-7 b\)

    Exercice\(\PageIndex{30}\)

    Multipliez :\((x+5)(x-y)\)

    Réponse

    \(x^{2}-x y+5 x-5 y\)

    Multipliez un binôme par un binôme en utilisant la méthode FOIL

    N'oubliez pas que lorsque vous multipliez un binôme par un binôme, vous obtenez quatre termes. Parfois, vous pouvez combiner des termes similaires pour obtenir un trinôme, mais parfois, comme dans Exercice\(\PageIndex{28}\), il n'y a pas de termes similaires à combiner.

    Regardons le dernier exemple et prêtons une attention particulière à la façon dont nous avons obtenu les quatre termes.

    \[\begin{array}{c}{(x-2)(x-y)} \\ {x^{2}-x y-2 x+2 y}\end{array} \nonumber\]

    D'où vient le premier mandat ?\(x^{2}\)

    Cette figure explique comment multiplier un binôme à l'aide de la méthode FOIL. Il comporte deux colonnes, avec des instructions écrites à gauche et des instructions mathématiques à droite. En haut de la figure, le texte de la colonne de gauche indique « C'est le produit de x et x, les premiers termes de x moins 2 et x moins y ». Dans la colonne de droite se trouve le produit de x moins 2 et x moins y. Une flèche part du x en x moins 2 et se termine au x en x moins y. En dessous se trouve le mot « Premier ». Une ligne plus bas, le texte de la colonne de gauche indique « Les termes suivants, négatif xy, sont le produit de x et de moins y, les deux termes extérieurs ». Dans la colonne de droite se trouve le produit de x moins 2 et de x moins y, avec une autre flèche allant du x en x moins 2 au y en x moins y. En dessous se trouve le mot « Extérieur ». Une ligne plus bas, le texte de la colonne de gauche indique « Le troisième terme, moins 2 x, est le produit de moins 2 et x, les deux termes internes ». Dans la colonne de droite se trouve le produit de x moins 2 et de x moins y avec une troisième flèche partant de moins 2 en x moins 2 et se terminant par le x en x moins y. En dessous se trouve le mot « Intérieur ». Dans la dernière rangée, le texte de la colonne de gauche indique « Et le dernier terme, plus 2 ans, provient de la multiplication des deux derniers termes, moins 2 et moins y ». Dans la colonne de droite se trouve le produit de x moins 2 et x moins y, avec une quatrième flèche allant du moins 2 dans x moins 2 au moins y dans x moins y. En dessous se trouve le mot « Dernier ».

    Nous abrégeons « First, Outer, Inner, Last » en FOIL. Les lettres signifient « F first, O outer, I inner, L ast ». Le mot FOIL est facile à retenir et permet de trouver les quatre produits.

    \[\begin{array}{c}{(x-2)(x-y)} \\ {x^{2}-x y-2 x+2 y} \\ {F \qquad O\qquad I\qquad L}\end{array}\]

    Regardons (x+3) (x+7).

    Propriété distributive DÉJOUER
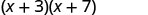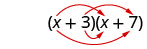    Le produit de x plus 3 et de x plus 7. Produit de x plus 3 et x plus y. Une flèche s'étend du x dans x plus 3 jusqu'au x dans x plus 7. Une deuxième flèche s'étend du x dans x plus 3 jusqu'au 7 dans x plus 7. Une troisième flèche s'étend du 3 en x plus 3 au x en x plus 7. Une quatrième flèche s'étend du 3 en x plus 3 au 7 en x plus 7.
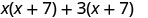    La somme de deux produits, le produit de x et x plus 7, et le produit de 3 et x plus 7.  
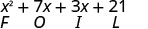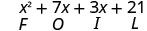    x au carré plus 7 x plus 3 x plus 21. En dessous de x au carré se trouve la lettre F, en dessous de 7 x est la lettre O, en dessous de 3 x est la lettre I et en dessous de 21 se trouve la lettre L, orthographiée FOIL. x au carré plus 7 x plus 3 x plus 21. En dessous de x au carré se trouve la lettre F, en dessous de 7 x est la lettre O, en dessous de 3 x est la lettre I et en dessous de 21 se trouve la lettre L, orthographiée FOIL.
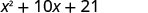    x au carré plus 10 x plus 21. \(x^{2}+10 x+21\)

    Remarquez comment les termes de la troisième ligne correspondent au modèle FOIL.

    Nous allons maintenant faire un exemple où nous utilisons le modèle FOIL pour multiplier deux binômes.

    Exercice\(\PageIndex{31}\): How to Multiply a Binomial by a Binomial using the FOIL Method

    Multipliez selon la méthode FOIL :\((x+5)(x+9)\)

    Réponse

    Cette figure est un tableau composé de trois colonnes et de cinq lignes. La première colonne est une colonne d'en-tête qui contient les noms et les numéros de chaque étape. Les deuxième et troisième colonnes contiennent des données mathématiques. Dans la rangée supérieure du tableau, la première cellule de gauche indique « Étape 1. Multipliez les premiers termes. » La deuxième colonne contient le produit des binômes x plus 5 et x plus 9. En dessous se trouve le produit de x plus 5 et de x plus 9, avec une flèche allant du x dans le premier binôme au x dans le second binôme. La troisième colonne contient x au carré plus blanc plus blanc plus blanc plus blanc plus blanc. Sous le x carré se trouve la lettre F, et sous chacun des trois espaces se trouvent les lettres O, I et L, respectivement.
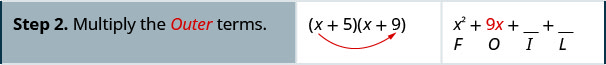
    Dans la deuxième rangée, la première cellule indique « Étape 2. Multipliez les termes extérieurs. » Dans la deuxième cellule se trouve le produit de x plus 5 et de x plus 9 à nouveau, avec une flèche allant de x dans le premier binôme au 9 dans le second binôme. La troisième cellule contient x au carré plus 9x plus un blanc et un blanc, avec la lettre F sous le x au carré, O sous le 9x et I et L sous les deux blancs.
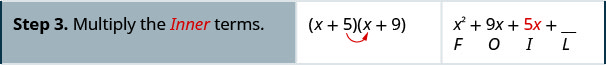
    Dans la troisième rangée, la première cellule indique « Étape 3. Multipliez les termes internes. » La deuxième cellule contient le produit de x plus 5 et de x plus 9, avec une flèche allant de 5 dans le premier binôme au x dans le second binôme. La troisième cellule contient x au carré plus 9x plus 5x plus un blanc, avec F en dessous de x au carré, O en dessous de 9x, I en dessous de 5x et L sous le blanc.
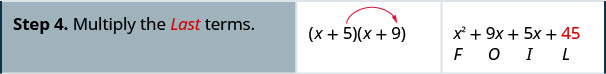
    Dans la quatrième rangée, la première cellule indique « Étape 4. Multipliez les derniers termes. » Dans la deuxième cellule se trouve le produit de x plus 5 et de x plus 9 à nouveau, avec une flèche allant de 5 dans le premier binôme à 9 dans le second binôme. La troisième cellule contient x au carré plus 9x plus 6x plus 45, avec F en dessous de x au carré, O en dessous de 9x, I en dessous de 6x et L en dessous de 45.
    Dans la dernière rangée, la première cellule indique « Étape 5. Combinez les mêmes termes, lorsque c'est possible. » La deuxième cellule est vide. La troisième cellule contient l'expression finale : x au carré plus 15x plus 45.

    Exercice\(\PageIndex{32}\)

    Multipliez selon la méthode FOIL :\((x+6)(x+8)\)

    Réponse

    \(x^{2}+14 x+48\)

    Exercice\(\PageIndex{33}\)

    Multipliez selon la méthode FOIL :\((y+17)(y+3)\)

    Réponse

    \(y^{2}+20 y+51\)

    Nous résumons les étapes de la méthode FOIL ci-dessous. La méthode FOIL ne s'applique qu'à la multiplication de binômes, pas d'autres polynômes !

    MULTIPLIEZ DEUX BINÔMES EN UTILISANT LA MÉTHODE FOIL
    .

    Lorsque vous multipliez par la méthode FOIL, tracer les lignes aidera votre cerveau à se concentrer sur le motif et à le rendre plus facile à appliquer.

    Exercice\(\PageIndex{34}\)

    Multipliez :\((y−7)(y+4)\).

    Réponse

    Cette figure comporte trois colonnes, avec des instructions écrites dans la première colonne et des instructions mathématiques dans les deuxième et troisième colonnes. En haut de la figure, le texte de la première colonne indique « Multipliez les premiers termes ». La deuxième colonne contient le produit de deux binômes, y moins 7 et y plus 4, avec une flèche allant du y dans le premier binôme au y dans le second binôme. La troisième colonne contient y au carré plus un blanc plus un blanc plus un blanc. Sous y au carré se trouve la lettre F et sous chaque blanc se trouvent les lettres O, I et L, respectivement. Une ligne plus bas, le texte de la première colonne indique « Multipliez les termes externes ». La deuxième colonne contient le produit de y moins 7 et de y plus 4, avec une deuxième flèche allant de y dans le premier binôme à 4 dans le second binôme. La troisième colonne contient y au carré plus 4 y plus un blanc plus un blanc. En dessous de y au carré se trouve F, en dessous de 4y est O et en dessous des blancs se trouvent I et L. Une ligne plus bas, le texte de la première colonne indique « Multipliez les termes internes ». La colonne du milieu contient le produit de y moins 7 et de y plus 4, avec une troisième flèche allant du moins 7 dans le premier binôme au y dans le second binôme. La troisième colonne contient y au carré plus 4 y moins 7 ans plus un espace vide. Une ligne plus bas, le texte de la première colonne indique « Multipliez les derniers termes ». La deuxième colonne contient le produit de y moins 7 et de y plus 4, avec une quatrième flèche allant de moins 7 dans le premier binôme à 4 dans le second binôme. Dans la troisième colonne se trouve l'expression complète, y au carré plus 4y moins 7y moins 28, avec chaque lettre de FOIL sous chacun des termes. Au bas de l'image, le texte de la première colonne indique « Combiner des termes similaires ». Dans la colonne de droite se trouve y au carré moins 3 y moins 28.

    Exercice\(\PageIndex{35}\)

    Multipliez :\((x−7)(x+5)\).

    Réponse

    \(x^{2}-2 x-35\)

    Exercice\(\PageIndex{36}\)

    Multipliez : (b−3) (b+6).

    Réponse

    \(b^{2}+3 b-18\)

    Exercice\(\PageIndex{37}\)

    Multipliez :\((4x+3)(2x−5)\).

    Réponse

    Cette figure comporte trois colonnes. En haut de la figure, la deuxième colonne contient le produit de deux binômes, 4x plus 3 et 2x moins 5. Une ligne plus bas, le texte de la première colonne indique « Multipliez les premiers termes. 4 fois 2 ». La deuxième colonne contient 8 fois le carré plus le blanc plus le blanc plus le blanc et le blanc. Sous 8x au carré se trouve la lettre F et sous chaque blanc se trouvent les lettres O, I et L, respectivement. Une ligne plus bas, le texte de la première colonne indique « Multipliez les termes extérieurs. 4 fois moins 5 ». La deuxième colonne contient 8 fois le carré moins 20 fois plus le blanc et le blanc. En dessous de 8x au carré se trouve F, en dessous de 20x est O et en dessous des blancs se trouvent I et L. Une ligne plus bas, le texte de la première colonne dit « Multipliez les termes internes. 3 fois 2x ». La deuxième colonne contient 8x au carré moins 20x plus 6x plus un blanc. Une ligne plus bas, le texte de la première colonne indique « Multipliez les derniers termes. 3 fois moins 5 ». La deuxième colonne contient l'expression complète, 8x au carré moins 20x plus 6x moins 15, avec chaque lettre de FOIL sous chacun des termes. Au bas de l'image, le texte de la première colonne indique « Combiner des termes similaires ». Dans la colonne de droite, il y a 8x au carré moins 14x moins 15. Dans la troisième colonne se trouve à nouveau le produit des deux binômes, 4x plus 3 fois 2x moins 5. Une flèche s'étend de 4x dans le premier binôme à 2x dans le second binôme. Une seconde flèche s'étend de 4x dans le premier binôme à moins 5 dans le second binôme. Une troisième flèche s'étend de 3 dans le premier binôme à 2x dans le second binôme. Une quatrième flèche s'étend de 3 dans le premier binôme à moins 5 dans le second binôme.

    Exercice\(\PageIndex{38}\)

    Multipliez :\((3x+7)(5x−2)\).

    Réponse

    \(15 x^{2}+29 x-14\)

    Exercice\(\PageIndex{39}\)

    Multipliez :\((4y+5)(4y−10)\).

    Réponse

    \(16 y^{2}-20 y-50\)

    Les produits finaux des quatre derniers exemples étaient des trinômes, car nous pouvions combiner les deux termes intermédiaires. Ce n'est pas toujours le cas.

    Exercice\(\PageIndex{40}\)

    Multipliez :\((3x−y)(2x−5)\).

    Réponse
      \((3 x-y)(2 x-5)\)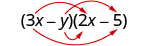
      Une flèche s'étend de 3 x dans le premier binôme à 2 x dans le second binôme. Une seconde flèche s'étend de 3 x dans le premier binôme à moins 5 dans le second binôme. Une troisième flèche s'étend de y dans le premier binôme à 2 x dans le second binôme. Une quatrième flèche s'étend de y dans le premier binôme à moins 5 dans le second binôme.
    Multipliez le premier. 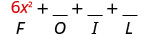6 carrés, plus blanc, blanc et blanc. En dessous de 6 x au carré se trouve la lettre F.
    Multipliez l'extérieur. 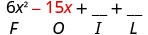6 x au carré moins 15 x plus le blanc et le blanc. Sous 15 x se trouve la lettre O.
    Multipliez l'intérieur. 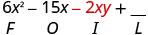6 x au carré moins 15 x moins 2 x plus le blanc. Sous moins 2 x y se trouve la lettre I.
    Multipliez le dernier. 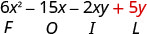6 x au carré moins 15 x moins 2 x y plus 5 y. Sous 5 y se trouve la lettre L.
    Combinez les mêmes termes, il n'y en a pas. \(6 x^{2}-15 x-2 x y+5 y\)
    Exercice\(\PageIndex{41}\)

    Multipliez : (10c−d) (c−6).

    Réponse

    \(10 c^{2}-60 c-c d+6 d\)

    Exercice\(\PageIndex{42}\)

    Multipliez : (7x−y) (2x−5).

    Réponse

    \(14 x^{2}-35 x-2 x y+10 y\)

    Faites attention aux exposants de l'exemple suivant.

    Exercice\(\PageIndex{43}\)

    Multipliez :\(\left(n^{2}+4\right)(n-1)\)

    Réponse
      \(\left(n^{2}+4\right)(n-1)\)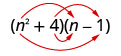
      Le produit de deux binômes, n au carré plus 4 et n moins 1. Une flèche s'étend de n au carré dans le premier binôme à n dans le second binôme. Une seconde flèche s'étend de n au carré dans le premier binôme à moins 1 dans le second binôme. Une troisième flèche s'étend de 4 dans le premier binôme à n dans le second binôme. Une quatrième flèche s'étend de 4 dans le premier binôme à moins 1 dans le second binôme.
    Multipliez le premier. 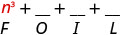n cubes plus blanc plus blanc plus blanc plus blanc. Sous n cubique se trouve la lettre F.
    Multipliez l'extérieur. 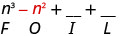n cubes moins n au carré plus blanc plus blanc plus blanc. Sous moins n au carré se trouve la lettre O.
    Multipliez l'intérieur. 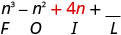n au cube moins n au carré plus 4 n plus le blanc. Sous 4 n se trouve la lettre I.
    Multipliez le dernier. 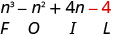n au cube moins n au carré plus 4 n moins 4. Sous moins 4 se trouve la lettre L.
    Combinez les mêmes termes, il n'y en a pas. \ (\ n^ {3} -n^ {2} +4 n-4)
    Exercice\(\PageIndex{44}\)

    Multipliez :\(\left(x^{2}+6\right)(x-8)\)

    Réponse

    \(x^{3}-8 x^{2}+6 x-48\)

    Exercice\(\PageIndex{45}\)

    Multipliez :\(\left(y^{2}+7\right)(y-9)\)

    Réponse

    \(y^{3}-9 y^{2}+7 y-63\)

    Exercice\(\PageIndex{46}\)

    Multipliez :\((3 p q+5)(6 p q-11)\)

    Réponse
      \((3 p q+5)(6 p q-11)\)  
    Multipliez le premier. 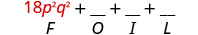18 p au carré q au carré plus blanc plus blanc plus blanc plus blanc. En dessous de 18 p au carré, q au carré se trouve la lettre F. Le produit de deux binômes, 3 p q plus 5 et 6 p q moins 11. Une flèche s'étend de 3 p q dans le premier binôme à 6 p q dans le second binôme. Une seconde flèche s'étend de 3 p q dans le premier binôme à moins 11 dans le second binôme. Une troisième flèche s'étend de 5 dans le premier binôme à 6 p q dans le second binôme. Une quatrième flèche s'étend de 5 dans le premier binôme à moins 11 dans le second binôme.
    Multipliez l'extérieur. 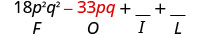18 p au carré q au carré moins 33 p q plus blanc plus blanc. En dessous de moins 33 p q se trouve la lettre O.
    Multipliez l'intérieur. 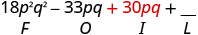18 p au carré q moins 33 p q plus 30 p q plus blanc. En dessous de 30 p q se trouve la lettre I.  
    Multipliez le dernier. 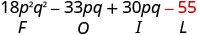18 p au carré q moins 33 p q plus 30 p q moins 55. En dessous de moins 55 se trouve la lettre L.  
    Combinez les mêmes termes, il n'y en a pas. \(18 p^{2} q^{2}-3 p q-55\)
    Exercice\(\PageIndex{47}\)

    Multipliez :\((2 a b+5)(4 a b-4)\)

    Réponse

    \(8 a^{2} b^{2}+12 a b-20\)

    Exercice\(\PageIndex{48}\)

    Multipliez :\((2 x y+3)(4 x y-5)\)

    Réponse

    \(8 x^{2} y^{2}+2 x y-15\)

    Multiplier un binôme par un binôme en utilisant la méthode verticale

    La méthode FOIL est généralement la méthode la plus rapide pour multiplier deux binômes, mais elle ne fonctionne que pour les binômes. Vous pouvez utiliser la propriété distributive pour trouver le produit de deux polynômes quelconques. Une autre méthode qui fonctionne pour tous les polynômes est la méthode verticale. Elle ressemble beaucoup à la méthode que vous utilisez pour multiplier des nombres entiers. Examinez attentivement cet exemple de multiplication de nombres à deux chiffres.

    Cette figure montre la multiplication verticale de 23 et 46. Le chiffre 23 est supérieur au chiffre 46. En dessous, il y a le produit partiel 138 au-dessus du produit partiel 92. Le produit final se trouve en bas et est de 1058. Le texte sur le côté droit de l'image dit « Commencez par multiplier 23 par 6 pour obtenir 138. Ensuite, multipliez 23 par 4 en alignant le produit partiel dans les bonnes colonnes. Enfin, vous ajoutez les produits partiels. »

    Nous allons maintenant appliquer cette même méthode pour multiplier deux binômes.

    Exercice\(\PageIndex{49}\)

    Multipliez en utilisant la méthode verticale :\((3 y-1)(2 y-6)\)

    Réponse

    Peu importe le binôme qui se trouve en haut.

    \[\begin{array}{lll}{\text { Multiply } 3 y-1 \text { by }-6 \text { . }}&& \\ {\text { Multiply } 3 y-1 \text { by } 2 y \text { . }}& &\\ \\ &{\qquad\space3 y-1} & \\& {\dfrac{ \space\space\times 2 y-6}{\quad-18 y+6}} & \text{partial product} & \\ &

    ParseError: EOF expected (click for details)
    Callstack:
    at (Francais/Livre_:_Algèbre_élémentaire_(OpenStax)/06:_Polynômes/6.03:_Multiplier_les_polynômes), /content/body/div[4]/div[3]/div[1]/div/dl/dd/p[2]/span/span, line 1, column 3
    & \text{partial product} & \\ \text{Add like terms.} &&\text{product} \end{array}\]

    Notez que les produits partiels sont identiques aux termes de la méthode FOIL.

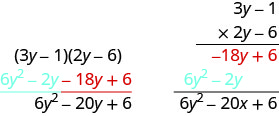
    Cette figure comporte deux colonnes. Dans la colonne de gauche se trouve le produit de deux binômes, 3y moins 1 et 2y moins 6. En dessous, il y a 6 ans au carré moins 2 ans moins 18 ans plus 6. En dessous, il y a 6 ans au carré moins 20 ans plus 6. Dans la colonne de droite se trouve la multiplication verticale de 3y moins 1 et de 2y moins 6. En dessous se trouve le produit partiel négatif 18y plus 6. En dessous se trouve le produit partiel 6 ans au carré moins 2 ans. En dessous, il y a 6 ans au carré moins 20 ans plus 6.

    Exercice\(\PageIndex{50}\)

    Multipliez en utilisant la méthode verticale :\((5 m-7)(3 m-6)\)

    Réponse

    \(15 m^{2}-51 m+42\)

    Exercice\(\PageIndex{51}\)

    Multipliez en utilisant la méthode verticale :\((6 b-5)(7 b-3)\)

    Réponse

    \(42 b^{2}-53 b+15\)

    Nous avons maintenant utilisé trois méthodes pour multiplier les binômes. Assurez-vous de pratiquer chaque méthode et essayez de décider laquelle vous préférez. Les méthodes sont répertoriées ici dans leur intégralité, pour vous aider à vous en souvenir.

    MULTIPLIER DEUX BINÔMES

    Pour multiplier des binômes, utilisez :

    • Propriété distributive
    • Méthode FOIL
    • Méthode verticale

    N'oubliez pas que FOIL ne fonctionne que lorsque vous multipliez deux binômes.

    Multipliez un trinôme par un binôme

    Nous avons multiplié les monômes par les monômes, les monômes par les polynômes et les binômes par les binômes. Nous sommes maintenant prêts à multiplier un trinôme par un binôme. N'oubliez pas que FOIL ne fonctionnera pas dans ce cas, mais nous pouvons utiliser la propriété distributive ou la méthode verticale. Nous examinons d'abord un exemple utilisant la propriété distributive.

    Exercice\(\PageIndex{52}\)

    Multipliez en utilisant la propriété distributive :\((b+3)\left(2 b^{2}-5 b+8\right)\)

    Réponse
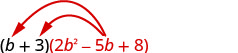
      Le produit d'un binôme, b plus 3, et d'un trinôme, 2 b au carré moins 5 b plus 8. Deux flèches partent du trinôme et se terminent en b et en 3 dans le binôme.
    Distribuez. 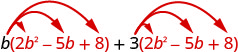La somme de deux produits, le produit de b et 2 b au carré moins 5 b plus 8, et le produit de 3 et 2 b au carré moins 5 b plus 8.
    Multipliez. \(2 b^{3}-5 b^{2}+8 b+6 b^{2}-15 b+24\)
    Combinez les mêmes termes. \(2 b^{3}+b^{2}-7 b+24\)
    Exercice\(\PageIndex{53}\)

    Multipliez en utilisant la propriété distributive :\((y-3)\left(y^{2}-5 y+2\right)\)

    Réponse

    \(y^{3}-8 y^{2}+17 y-6\)

    Exercice\(\PageIndex{54}\)

    Multipliez en utilisant la propriété distributive :\((x+4)\left(2 x^{2}-3 x+5\right)\)

    Réponse

    \(2 x^{3}+5 x^{2}-7 x+20\)

    Faisons maintenant la même multiplication en utilisant la méthode verticale.

    Exercice\(\PageIndex{55}\)

    Multipliez en utilisant la méthode verticale :\((b+3)\left(2 b^{2}-5 b+8\right)\)

    Réponse

    Il est plus facile de placer le polynôme avec moins de termes en bas, car nous obtenons ainsi moins de produits partiels.

    Multipliez\((2b^2 − 5b + 8)\) par 3. .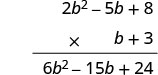
      .
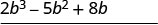
    Multipliez\((2b^2 − 5b + 8)\) par\(b\). \(2 b^{3}+b^{2}-7 b+24\)
    Ajoutez des termes similaires.
    Exercice\(\PageIndex{56}\)

    Multipliez en utilisant la méthode verticale :\((y-3)\left(y^{2}-5 y+2\right)\)

    Réponse

    \(y^{3}-8 y^{2}+17 y-6\)

    Exercice\(\PageIndex{57}\)

    Multipliez en utilisant la méthode verticale :\((x+4)\left(2 x^{2}-3 x+5\right)\)

    Réponse

    \(2 x^{3}+5 x^{2}-7 x+20\)

    Nous avons maintenant vu deux méthodes que vous pouvez utiliser pour multiplier un trinôme par un binôme. Après avoir pratiqué chaque méthode, vous constaterez probablement que vous préférez une méthode à l'autre. Nous listons que les deux méthodes sont répertoriées ici, pour faciliter la consultation.

    MULTIPLIER UN TRINÔME PAR UN BINÔME

    Pour multiplier un trinôme par un binôme, utilisez :

    • Propriété distributive
    • Méthode verticale
    Remarque

    Accédez à ces ressources en ligne pour obtenir des instructions et des exercices supplémentaires sur la multiplication des polynômes :

    • Multiplier les exposants 1
    • Multiplier les exposants 2
    • Multiplier les exposants 3

    Concepts clés

    • Méthode FOIL pour multiplier deux binômes —Pour multiplier deux binômes :
      1. Multipliez les premiers termes.
      2. Multipliez les termes extérieurs.
      3. Multipliez les termes internes.
      4. Multipliez les derniers termes.
    • Multiplier deux binômes —Pour multiplier des binômes, utilisez :
    • Multiplier un trinôme par un binôme —Pour multiplier un trinôme par un binôme, utilisez :