6.2 : Utiliser les propriétés de multiplication des exposants
- Page ID
- 195051
À la fin de cette section, vous serez en mesure de :
- Simplifier les expressions à l'aide
- Simplifier les expressions à l'aide de la propriété de produit pour
- Simplifiez les expressions en utilisant la propriété Power pour les exposants
- Simplifier les expressions en utilisant la propriété Product to a Power
- Simplifier les expressions en appliquant plusieurs propriétés
- Multiplier les monômes
Avant de commencer, répondez à ce questionnaire de préparation.
- Simplifier :\(\frac{3}{4}\cdot \frac{3}{4}\)
si vous avez oublié ce problème, passez en revue l'exercice 1.6.13. - Simplifiez :\((−2)(−2)(−2)\).
Si vous avez oublié ce problème, passez en revue l'exercice 1.5.13.
Simplifier les expressions à l'aide
N'oubliez pas qu'un exposant indique une multiplication répétée de la même quantité. Par exemple,\(2^4\) signifie le produit de\(4\) facteurs de\(2\), donc\(2^4\) signifie\(2·2·2·2\).
Revoyons le vocabulaire des expressions avec des exposants.
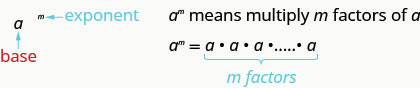
C'est lu\(a\) au\(m^{th}\) pouvoir.
Dans l'expression\(a^{m}\), l'exposant nous\(m\) indique combien de fois nous utilisons la base a comme facteur.

Avant de commencer à travailler avec des expressions variables contenant des exposants, simplifiez quelques expressions impliquant uniquement des nombres.
Simplifiez :
- \(4^{3}\)
- \(7^{1}\)
- \(\left(\frac{5}{6}\right)^{2}\)
- \((0.63)^{2}\)
- Réponse
-
- \(\begin{array}{ll} & 4^{3}\\ {\text { Multiply three factors of } 4 .} & {4 \cdot 4 \cdot 4} \\ {\text { Simplify. }} & {64}\end{array}\)
- \(\begin{array}{ll} & 7^{1}\\ \text{Multiply one factor of 7.} & 7\end{array}\)
- \(\begin{array}{ll} &\left(\frac{5}{6}\right)^{2}\\ {\text { Multiply two factors. }} & {\left(\frac{5}{6}\right)\left(\frac{5}{6}\right)} \\ {\text { Simplify. }} & {\frac{25}{36}}\end{array}\)
- \(\begin{array}{ll} &(0.63)^{2}\\ {\text { Multiply two factors. }} & {(0.63)(0.63)} \\ {\text { Simplify. }} & {0.3969}\end{array}\)
Simplifiez :
- \(6^{3}\)
- \(15^{1}\)
- \(\left(\frac{3}{7}\right)^{2}\)
- \((0.43)^{2}\)
- Réponse
-
- 216
- 15
- \(\frac{9}{49}\)
- 0,149
Simplifiez :
- \(2^{5}\)
- \(21^{1}\)
- \(\left(\frac{2}{5}\right)^{3}\)
- \((0.218)^{2}\)
- Réponse
-
- 32
- 21
- \(\frac{8}{125}\)
- 0,047524
Simplifiez :
- \((-5)^{4}\)
- \(-5^{4}\)
- Réponse
-
- \(\begin{array}{ll} &(-5)^{4}\\{\text { Multiply four factors of }-5} & {(-5)(-5)(-5)} \\ {\text { Simplify. }} & {625}\end{array}\)
- \(\begin{array}{ll} &-5^{4}\\{\text { Multiply four factors of } 5 .} & {-(5 \cdot 5 \cdot 5 \cdot 5)} \\ {\text { Simplify. }} & {-625}\end{array}\)
Remarquez les similitudes et les différences entre l'exemple\(\PageIndex{4}\) partie 1 et l'exemple\(\PageIndex{4}\) partie 2 ! Pourquoi les réponses sont-elles différentes ? Lorsque nous suivons l'ordre des opérations dans la partie 1, les parenthèses nous indiquent de l'élever\((−5)\) à la 4e puissance. Dans la deuxième partie, nous élevons juste la\(5\) 4e puissance, puis nous prenons l'inverse.
Simplifiez :
- \((-3)^{4}\)
- \(-3^{4}\)
- Réponse
-
- 81
- −81
Simplifiez :
- \((-13)^{4}\)
- \(-13^{4}\)
- Réponse
-
- 169
- −169
Simplifier les expressions à l'aide de la propriété de produit pour
Vous avez vu que lorsque vous combinez des termes similaires en les additionnant et en les soustrayant, vous devez avoir la même base avec le même exposant. Mais lorsque vous multipliez et divisez, les exposants peuvent être différents, et parfois les bases peuvent également être différentes.
Nous allons déduire les propriétés des exposants en recherchant des modèles dans plusieurs exemples.
Nous allons d'abord examiner un exemple qui mène à la propriété du produit.
 |
|
| Qu'est-ce que cela signifie ? Combien de facteurs au total ? |
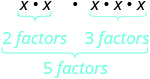 |
| Donc, nous avons | 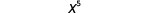 |
| Notez que 5 est la somme des exposants 2 et 3. | 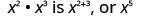 |
Nous écrivons :\[\begin{array}{c}{x^{2} \cdot x^{3}} \\ {x^{2+3}} \\ {x^{5}}\end{array}\]
La base est restée la même et nous avons ajouté les exposants. Cela conduit à la propriété de produit pour les exposants.
Si\(a\) c'est un nombre réel,\(m\) et que vous\(n\) comptez des nombres, alors
\[a^{m} \cdot a^{n}=a^{m+n}\]
Pour multiplier avec des bases similaires, ajoutez les exposants.
Un exemple avec des chiffres permet de vérifier cette propriété.
\[\begin{array}{rll} {2^3\cdot2^2} &\stackrel{?}{=} & 2^{2+3}\\ {4\cdot 8} &\stackrel{?}{=} & 2^{5} \\ {32} &=& 32\checkmark\end{array}\]
Simplifiez :\(y^{5} \cdot y^{6}\)
- Réponse
-
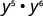
Utilisez la propriété du produit,\(a^{m} \cdot a^{n}=a^{m+n}\). 
Simplifiez. 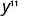
Simplifiez :\(b^{9} \cdot b^{8}\)
- Réponse
-
\(b^{17}\)
Simplifiez :\(x^{12} \cdot x^{4}\)
- Réponse
-
\(x^{16}\)
Simplifiez :
- \(2^{5} \cdot 2^{9}\)
- \(3\cdot 3^{4}\)
- Réponse
-
un.

Utilisez la propriété du produit,\(a^{m} \cdot a^{n}=a^{m+n}\). 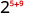
Simplifiez. 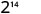
b.
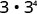
Utilisez la propriété du produit,\(a^{m} \cdot a^{n}=a^{m+n}\). 
Simplifiez. 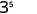
Simplifiez :
- \(5\cdot 5^{5}\)
- \(4^{9} \cdot 4^{9}\)
- Réponse
-
- \(5^{6}\)
- \(4^{18}\)
Simplifiez :
- \(7^{6} \cdot 7^{8}\)
- \(10 \cdot 10^{10}\)
- Réponse
-
- \(7^{14}\)
- \(10^{11}\)
Simplifiez :
- \(a^{7} \cdot a\)
- \(x^{27} \cdot x^{13}\)
- Réponse
-
un.
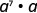
Réécrire,\(a = a^1\) 
Utilisez la propriété du produit,\(a^m\cdot a^n = a^{m+n}\). 
Simplifiez. 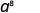
b.

Remarquez que les bases sont les mêmes, alors ajoutez les exposants. 
Simplifiez. 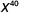
Simplifiez :
- \(p^{5} \cdot p\)
- \(y^{14} \cdot y^{29}\)
- Réponse
-
- \(p^{6}\)
- \(y^{43}\)
Simplifiez :
- \(z \cdot z^{7}\)
- \(b^{15} \cdot b^{34}\)
- Réponse
-
- \(z^{8}\)
- \(b^{49}\)
Nous pouvons étendre la propriété du produit pour les exposants à plus de deux facteurs.
Simplifiez :\(d^{4} \cdot d^{5} \cdot d^{2}\)
- Réponse
-
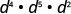
Ajoutez les exposants, car les bases sont les mêmes. 
Simplifiez. 
Simplifiez :\(x^{6} \cdot x^{4} \cdot x^{8}\)
- Réponse
-
\(x^{18}\)
Simplifiez :\(b^{5} \cdot b^{9} \cdot b^{5}\)
- Réponse
-
\(b^{19}\)
Simplifier les expressions en utilisant la propriété Power pour les exposants
Examinons maintenant une expression exponentielle qui contient une puissance portée à une puissance. Voyez si vous pouvez découvrir une propriété générale.
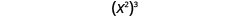 |
|
| Qu'est-ce que cela signifie ? Combien de facteurs au total ? |
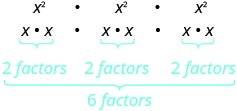 |
| Nous avons donc | 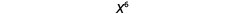 |
| Notez que 6 est le produit des exposants 2 et 3. | 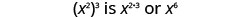 |
Nous écrivons :
\[\begin{array}{c}{\left(x^{2}\right)^{3}} \\ {x^{2 \cdot 3}} \\ {x^{6}}\end{array}\]
Nous avons multiplié les exposants. Cela conduit à la propriété Power pour les exposants.
Si\(a\) est un nombre réel et que\(m\) et\(n\) sont des nombres entiers, alors
\[\left(a^{m}\right)^{n}=a^{m \cdot n}\]
Pour élever une puissance à une puissance, multipliez les exposants.
Un exemple avec des chiffres permet de vérifier cette propriété.
\[\begin{array} {lll} \left(3^{2}\right)^{3} &\stackrel{?}{=}&3^{2 \cdot 3} \\(9)^{3} &\stackrel{?}{=} & 3^{6} \\ 729 &=&729\checkmark \end{array}\]
Simplifiez :
- \(\left(y^{5}\right)^{9}\)
- \(\left(4^{4}\right)^{7}\)
- Réponse
-
un.
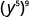
Utilisez la propriété power,\(\big(a^m\big)^n = a^{m\cdot n}\). 
Simplifiez. 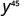
b.
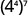
Utilisez la propriété power. 
Simplifiez. 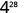
Simplifiez :
- \( \left(b^{7}\right)^{5} \)
- \(\left(5^{4}\right)^{3}\)
- Réponse
-
- \( b^{35}\)
- \(5^{12}\)
Simplifiez :
- \(\left(z^{6}\right)^{9}\)
- \(\left(3^{7}\right)^{7}\)
- Réponse
-
- \(z^{54}\)
- \(3^{49}\)
Simplifier les expressions en utilisant le produit pour une propriété de puissance
Nous allons maintenant examiner une expression contenant un produit qui est élevé à une puissance. Pouvez-vous trouver ce modèle ?
\(\begin{array}{ll}{\text { What does this mean? }} & {\text { (2x) }^{3}} \\ {\text { We group the like factors together. }} & {2 x \cdot 2 x \cdot 2 x} \\ {\text { How many factors of } 2 \text { and of } x ?} & {2 \cdot 2 \cdot x^{3}} \\ {\text { Notice that each factor was raised to the power and }(2 x)^{3} \text { is } 2^{3} \cdot x^{3}}\end{array}\)
\(\begin{array}{ll}\text{We write:} & {(2 x)^{3}} \\ & {2^{3} \cdot x^{3}}\end{array}\)
L'exposant s'applique à chacun des facteurs ! Cela conduit au produit à une propriété de puissance pour les exposants.
Si\(a\) et\(b\) sont des nombres réels et\(m\) un nombre entier, alors
\[(a b)^{m}=a^{m} b^{m}\]
Pour élever un produit à une puissance, augmentez chaque facteur à cette puissance.
Un exemple avec des chiffres permet de vérifier cette propriété :
\ [\ begin {array} {lll} (2 \ cdot 3) ^ {2} & \ stackrel {?} {=} &2^ {2} \ cdot 3^ {2} \ \ 6^ {2} & \ stackrel {?} {=} &4 \ cdot 9 \ \ 36 &=&36
\ checkmark \ end {array} \]
Simplifiez :
- \((-9 d)^{2}\)
- \((3mn)^{3}\).
- Réponse
-
un.
b.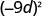
Utiliser la puissance d'une propriété du produit,\((ab)^m=a^m b^m\). 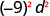
Simplifiez. 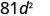
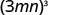
Utiliser la puissance d'une propriété du produit,\((ab)^m=a^m b^m\). 
Simplifiez. 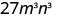
Simplifiez :
- \((-12 y)^{2}\)
- \((2 w x)^{5}\)
- Réponse
-
- \(144y^{2}\)
- \(32w^{5} x^{5}\)
Simplifiez :
- \((5 w x)^{3}\)
- \((-3 y)^{3}\)
- Réponse
-
- 125\(w^{3} x^{3}\)
- \(-27 y^{3}\)
Simplifier les expressions en appliquant plusieurs propriétés
Nous disposons désormais de trois propriétés permettant de multiplier des expressions par des exposants. Résumons-les, puis nous donnerons quelques exemples qui utilisent plusieurs propriétés.
Si\(a\) et\(b\) sont des nombres réels, et\(m\) et\(n\) sont des nombres entiers, alors
\[\begin{array}{llll} \textbf{Product Property } & a^{m} \cdot a^{n}&=&a^{m+n} \\ \textbf {Power Property } &\left(a^{m}\right)^{n}&=&a^{m n} \\ \textbf {Product to a Power } &(a b)^{m}&=&a^{m} b^{m} \end{array}\]
Toutes les propriétés des exposants sont vraies pour tous les nombres réels\(m\) et\(n\). À l'heure actuelle, nous n'utilisons que des exposants entiers.
Simplifiez :
- \(\left(y^{3}\right)^{6}\left(y^{5}\right)^{4}\)
- \(\left(-6 x^{4} y^{5}\right)^{2}\)
- Réponse
-
- \(\begin{array}{ll}& \left(y^{3}\right)^{6}\left(y^{5}\right)^{4}\\ {\text { Use the Power Property. }}& y^{18} \cdot y^{20} \\ {\text { Add the exponents. }} & y^{38} \end{array}\)
- \(\begin{array}{ll}& \left(-6 x^{4} y^{5}\right)^{2}\\ {\text { Use the Product to a Power Property. }} & {(-6)^{2}\left(x^{4}\right)^{2}\left(y^{5}\right)^{2}} \\ {\text { Use the Power Property. }} & {(-6)^{2}\left(x^{8}\right)\left(y^{10}\right)^{2}} \\ {\text { Simplify. }} & {36 x^{8} y^{10}}\end{array}\)
Simplifiez :
- \(\left(a^{4}\right)^{5}\left(a^{7}\right)^{4}\)
- \(\left(-2 c^{4} d^{2}\right)^{3}\)
- Réponse
-
- \(a^{48}\)
- \(-8 c^{12} d^{6}\)
Simplifiez :
- \(\left(-3 x^{6} y^{7}\right)^{4}\)
- \(\left(q^{4}\right)^{5}\left(q^{3}\right)^{3}\)
- Réponse
-
- 81\(x^{24} y^{28}\)
- \(q^{29}\)
Simplifiez :
- \((5 m)^{2}\left(3 m^{3}\right)\)
- \(\left(3 x^{2} y\right)^{4}\left(2 x y^{2}\right)^{3}\)
- Réponse
-
- \(\begin{array}{ll}& (5 m)^{2}\left(3 m^{3}\right)\\{\text { Raise } 5 m \text { to the second power. }} & {5^{2} m^{2} \cdot 3 m^{3}} \\ {\text { Simplify. }} & {25 m^{2} \cdot 3 m^{3}} \\ {\text { Use the Commutative Property. }} & {25 \cdot 3 \cdot m^{2} \cdot m^{3}} \\ {\text { Multiply the constants and add the exponents. }} & {75 m^{5}}\end{array}\)
- \(\begin{array}{ll} & \left(3 x^{2} y\right)^{4}\left(2 x y^{2}\right)^{3} \\ \text{Use the Product to a Power Property.} & \left(3^{4} x^{8} y^{4}\right)\left(2^{3} x^{3} y^{6}\right)\\\text{Simplify.} & \left(81 x^{8} y^{4}\right)\left(8 x^{3} y^{6}\right)\\ \text{Use the Commutative Property.} &81\cdot 8 \cdot x^{8} \cdot x^{3} \cdot y^{4} \cdot y^{6} \\\text{Multiply the constants and add the exponents.} & 648x^{11} y^{10}\\ \end{array}\)
Simplifiez :
- \((5 n)^{2}\left(3 n^{10}\right)\)
- \(\left(c^{4} d^{2}\right)^{5}\left(3 c d^{5}\right)^{4}\)
- Réponse
-
- 75\(n^{12}\)
- 81\(c^{24} d^{30}\)
Simplifiez :
- \(\left(a^{3} b^{2}\right)^{6}\left(4 a b^{3}\right)^{4}\)
- \((2 x)^{3}\left(5 x^{7}\right)\)
- Réponse
-
- 256\(a^{22} b^{24}\)
- 40\(x^{10}\)
Multiplier les monômes
Comme un monomial est une expression algébrique, nous pouvons utiliser les propriétés des exposants pour multiplier les monômes.
Multipliez :\(\left(3 x^{2}\right)\left(-4 x^{3}\right)\)
- Réponse
-
\ (\ begin {array} {ll} & \ left (3 x^ {2} \ right) \ left (-4 x^ {3} \ right) \ \ \ text {Utilisez la propriété de commutation pour réorganiser les termes.} & 3 \ cdot (-4) \ cdot x^ {2} \ cdot x^ {3} \ \
\ text {Multipliez.} & -12 x^ {5} \ end {tableau} \)
Multipliez :\(\left(5 y^{7}\right)\left(-7 y^{4}\right)\)
- Réponse
-
\(-35 y^{11}\)
Multipliez :\(\left(-6 b^{4}\right)\left(-9 b^{5}\right)\)
- Réponse
-
54\(b^{9}\)
Multipliez :\(\left(\frac{5}{6} x^{3} y\right)\left(12 x y^{2}\right)\)
- Réponse
-
\(\begin{array}{ll} & \left(\frac{5}{6} x^{3} y\right)\left(12 x y^{2}\right)\\ \text{Use the Commutative Property to rearrange the terms.} & \frac{5}{6} \cdot 12 \cdot x^{3} \cdot x \cdot y \cdot y^{2}\\ \text{Multiply.} &10x^{4} y^{3}\end{array}\)
Multipliez :\(\left(\frac{2}{5} a^{4} b^{3}\right)\left(15 a b^{3}\right)\)
- Réponse
-
6\(a^{5} b^{6}\)
Multipliez :\(\left(\frac{2}{3} r^{5} s\right)\left(12 r^{6} s^{7}\right)\)
- Réponse
-
8\(r^{11} s^{8}\)
Accédez à ces ressources en ligne pour obtenir des instructions supplémentaires et vous entraîner à utiliser les propriétés de multiplication des exposants :
- Propriétés de multiplication des exposants
Concepts clés
- Notation exponentielle
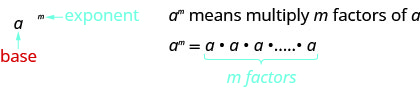
- Propriétés des exposants
- Si\(a\) et\(b\) sont des nombres réels\(m\) et\(n\) des nombres entiers, alors
\[\begin{array}{llll} \textbf{Product Property } & a^{m} \cdot a^{n}&=&a^{m+n} \\ \textbf {Power Property } &\left(a^{m}\right)^{n}&=&a^{m n} \\ \textbf {Product to a Power } &(a b)^{m}&=&a^{m} b^{m} \end{array}\]


