4.3 : Graphe avec interceptions

Last updated
Save as PDF

Page ID: 194789

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objectifs d'apprentissage

À la fin de cette section, vous serez en mesure de :

Identifiez les interceptions x et y sur un graphique
Trouvez les interceptions x et y à partir de l'équation d'une droite
Tracez une ligne à l'aide des interceptions

Remarque

Avant de commencer, répondez à ce questionnaire de préparation.

Résoudre :$3\cdot 0+4y=−2$.
Si vous avez oublié ce problème, passez en revue l'exercice 2.2.13.

Identifier les interceptions x et y sur un graphique

Chaque équation linéaire peut être représentée par une ligne unique qui montre toutes les solutions de l'équation. Nous avons vu que lorsque vous tracez une ligne en traçant des points, vous pouvez utiliser trois solutions quelconques pour représenter graphiquement. Cela signifie que deux personnes qui tracent la ligne peuvent utiliser différents ensembles de trois points.

À première vue, leurs deux lignes peuvent ne pas sembler identiques, car des points différents seraient étiquetés. Mais si tout le travail a été fait correctement, les lignes devraient être exactement les mêmes. Une façon de reconnaître qu'il s'agit bien de la même droite est de regarder où la droite croise l'axe x et l'axe y. Ces points sont appelés les points d'intersection de la ligne.

INTERCEPTIONS D'UNE LIGNE

Les points où une ligne croise l'axe x et l'axe y sont appelés points d'intersection d'une ligne.

Regardons les graphiques des lignes de la figure$\PageIndex{1}$.

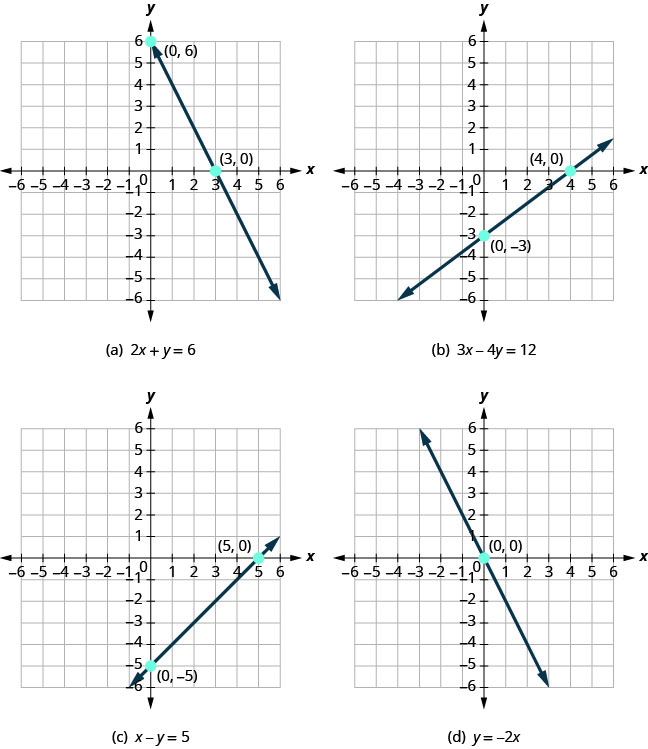
Quatre figures, chacune représentant une ligne droite différente sur le plan de coordonnées x y. L'axe X des plans va de moins 7 à 7. L'axe y des plans va de moins 7 à 7. La figure a montre une ligne droite croisant l'axe x au point (3, 0) et croisant l'axe y au point (0, 6). Le graphique est étiqueté avec l'équation 2x plus y égale 6. La figure b montre une ligne droite croisant l'axe x au point (4, 0) et croisant l'axe y au point (0, moins 3). Le graphique est étiqueté avec l'équation 3x moins 4y égale 12. La figure c montre une ligne droite croisant l'axe x au point (5, 0) et croisant l'axe y au point (0, moins 5). Le graphique est étiqueté avec l'équation x moins y égale 5. La figure d montre une ligne droite croisant les axes x et y au point (0, 0). Le graphique est étiqueté avec l'équation y égale moins 2x. — Figure$\PageIndex{1}$ : Exemples de graphes croisant l'axe X négatif.

Tout d'abord, remarquez où chacune de ces lignes croise l'axe x négatif. Voir la figure$\PageIndex{1}$.

Tableau$\PageIndex{1}$
Figurine	La ligne traverse l'axe X à :	Paire commandée de ce point
Figure (a)	3	(3,0)
Graphique (b)	4	(4,0)
Figure (c)	5	(5,0)
Chiffre (d)	0	(0,0)

Voyez-vous un schéma ?

Pour chaque ligne, la coordonnée y du point où la ligne croise l'axe x est nulle. Le point où la ligne croise l'axe x a la forme (a,0) et s'appelle l'intersection x d'une droite. L'intersection x - se produit lorsque y est égal à zéro. Maintenant, regardons les points où ces lignes croisent l'axe y. Voir le tableau$\PageIndex{2}$.

Tableau$\PageIndex{2}$
Figurine	La ligne traverse l'axe X à l'endroit suivant :	Paire commandée de ce point
Figure (a)	6	(0,6)
Graphique (b)	−3	(0, −3)
Figure (c)	−5	(0,5)
Chiffre (d)	0	(0,0)

Quel est le schéma ici ?

Dans chaque ligne, la coordonnée x du point où la ligne croise l'axe y est nulle. Le point où la droite croise l'axe y a la forme (0, b) et s'appelle l'intersection y de la droite. L'intersection y - se produit lorsque x est égal à zéro.

INTERCEPTION X ET INTERCEPTION Y D'UNE LIGNE

L'intersection x est le point (a,0) où la ligne croise l'axe des x.

L'intersection y est le point (0, b) où la ligne croise l'axe y.

Pas de texte alternatif — Figurine$\PageIndex{2}$

Exercice$\PageIndex{1}$

Trouvez les points d'intersection x et y sur chaque graphique.

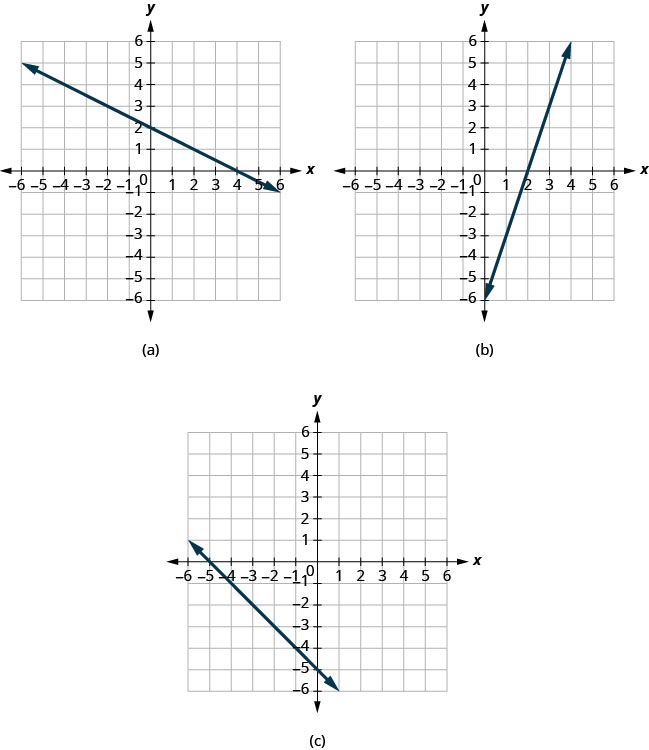
Trois figures, chacune représentant une ligne droite différente sur le plan de coordonnées x y. L'axe X des plans va de moins 7 à 7. L'axe y des plans va de moins 7 à 7. La figure a montre une ligne droite passant par les points (négatif 6, 5), (négatif 4, 4), (négatif 2, 3), (0, 2), (2, 1), (4, 0) et (6, négatif 1). La figure b montre une ligne droite passant par les points (0, moins 6), (1, moins 3), (2, 0), (3, 3) et (4, 6). La figure c montre une ligne droite passant par les points (négatif 6, 1), (négatif 5, 0), (négatif 4, négatif 1), (négatif 3, négatif 2), (négatif 2, négatif 3), (négatif 1, négatif 4), (0, négatif 5) et (1, négatif 6). — Figurine$\PageIndex{3}$

Réponse: (a) Le graphique croise l'axe des X au point (4,0). L'intersection x - est (4,0).
Le graphique traverse l'axe y au point (0,2). L'intersection y - est (0,2).

(b) Le graphique croise l'axe des X au point (2,0). L'intersection x est (2,0).
Le graphique croise l'axe y au point (0, −6). L'intersection y - est (0, −6).

(c) Le graphique croise l'axe x au point (−5,0). L'intersection x - est (−5,0).
Le graphique traverse l'axe y au point (0, −5). L'intersection y - est (0, −5).

Exercice$\PageIndex{2}$

Trouvez les points d'intersection x et y sur le graphique.

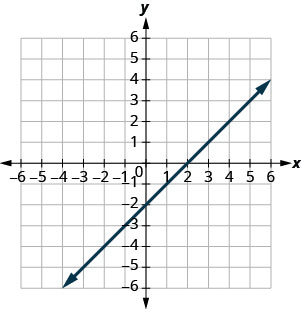
$Figure représentant une ligne droite sur le plan de coordonnées x y. L'axe X du plan va de moins 10 à 10. L'axe y des plans va de moins 10 à 10. La ligne droite passe par les points (négatif 8, négatif 10), (négatif 6, négatif 8), (négatif 4, négatif 6), (négatif 2, négatif 4), (0, négatif 2), (2, 0), (4, 2), (6, 4), (8, 6) et (10, 8).$

Réponse: x - interception : (2,0) ; y - interception : (0, −2)

Exercice$\PageIndex{3}$

Trouvez les points d'intersection x et y sur le graphique.

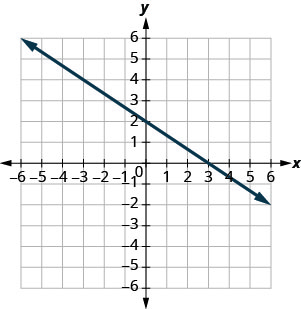
$La figure montre une ligne droite sur le plan de coordonnées x y. L'axe X du plan va de moins 10 à 10. L'axe y des plans va de moins 10 à 10. La ligne droite passe par les points (négatif 9, 8), (négatif 6, 6), (négatif 3, 4), (0, 2), (3, 0), (6, négatif 2) et (9, négatif 4).$

Réponse: x - interception : (3,0), y - interception : (0,2)

Trouvez les interceptions x et y à partir de l'équation d'une droite

Reconnaître que l'intersection x se produit lorsque y est nul et que l'intersection y se produit lorsque x est zéro, nous donne une méthode pour trouver les interceptions d'une droite à partir de son équation. Pour trouver l'intersection x -, laissez y=0 et résolvez pour x. Pour trouver l'intersection y -, laissez x=0 et résolvez pour y.

X- ET Y - INTERCEPTIONS À PARTIR DE L'ÉQUATION D'UNE DROITE

Utilisez l'équation de la droite. Pour trouver :

l'intersection x - de la ligne, soit y=0 et résolvez pour x.
l'intersection y - de la ligne, soit x=0 et résolvez pour y.

Exercice$\PageIndex{4}$

Trouvez les points d'intersection de 2x+y=6.

Réponse

Nous allons laisser y=0 pour trouver l'intersection x, et x=0 pour trouver l'intersection y -. Nous allons remplir le tableau, qui nous rappelle ce que nous devons trouver.

$La figure montre un tableau composé de quatre lignes et de deux colonnes. La première ligne est une ligne de titre et elle étiquette le tableau avec l'équation 2 x plus y est égal à 6. La deuxième ligne est une ligne d'en-tête et elle étiquette chaque colonne. L'en-tête de la première colonne est « x » et le second est « y ». La troisième ligne est intitulée « X- Intercept » ; la première colonne est vide et la deuxième colonne a un 0. La quatrième ligne est intitulée « Interception y » et comporte un 0 dans la première colonne, la deuxième colonne étant vide.$

Pour trouver l'intersection x -, soit y=0.

Tableau$\PageIndex{3}$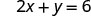
	$.$
Soit y = 0.	$.$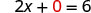
Simplifiez.	$.$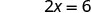
	$.$
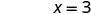
L'intersection x est	(3, 0)
Pour trouver l'intersection y, soit x = 0.
	$.$
Soit x = 0.	$.$
Simplifiez.	$.$
	$.$
L'intersection y est	(0, 6)

Les points d'interception sont les points (3,0) et (0,6), comme indiqué dans le tableau$\PageIndex{4}$.

Tableau$\PageIndex{4}$
2x+y=6
x	y
3	0
0	6

Exercice$\PageIndex{5}$

Trouvez les points d'intersection de 3x+y=12.

Réponse: x - interception : (4,0), y - interception : (0,12)

Exercice$\PageIndex{6}$

Détermine les points d'intersection de x+4y=8.

Réponse: x - interception : (8,0), y - interception : (0,2)

Exercice$\PageIndex{7}$

Trouvez les points d'intersection de 4x—3y=12.

Réponse

Pour trouver l'intersection x, laissez y = 0.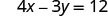
	$.$
Soit y = 0.	$.$
Simplifiez.	$.$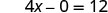
	$.$
	$.$
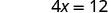
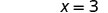
L'intersection x est	(3, 0)
Pour trouver l'intersection y, soit x = 0.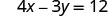
	$.$
Soit x = 0.	$.$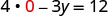
Simplifiez.	$.$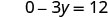
	$.$
	$.$
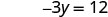
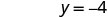
L'intersection y est	(0, −4)

Tableau$\PageIndex{5}$

Les points d'interception sont les points (3, 0) et (0, −4) comme indiqué dans le tableau suivant.

Tableau$\PageIndex{6}$
4x−3 y=12
x	y
3	0
0	−4

Exercice$\PageIndex{8}$

Trouvez les points d'intersection de 3x—4y=12.

Réponse: x - interception : (4,0), y - interception : (0, −3)

Exercice$\PageIndex{9}$

Trouvez les points d'intersection de 2x—4y=8.

Réponse: x - interception : (4,0), y - interception : (0, −2)

Tracez une ligne à l'aide des interceptions

Pour représenter graphiquement une équation linéaire en traçant des points, vous devez trouver trois points dont les coordonnées sont des solutions à l'équation. Vous pouvez utiliser les interceptions x et y comme deux de vos trois points. Trouvez les points d'interception, puis trouvez un troisième point pour garantir la précision. Assurez-vous que les points s'alignent, puis tracez la ligne. Cette méthode est souvent la méthode la plus rapide pour tracer une ligne.

Exercice$\PageIndex{10}$: How to Graph a Line Using Intercepts

Graphe —x+2y=6 en utilisant les interceptions.

Réponse: $La figure montre un tableau avec la procédure générale pour tracer une ligne à l'aide des interceptions, ainsi qu'un exemple spécifique utilisant l'équation négative x plus 2y égale 6. L'étape 1 de la procédure générale est la suivante : « Trouvez les interceptions x et y de la ligne. Soit y est égal à 0 et résolvez pour x. Soit x est égal à 0 et résolvez pour y ». L'étape 1 de l'exemple est une série d'instructions et d'équations : « Trouvez l'intersection X. Soit y égal 0 », moins x plus 2y est égal à 6, moins x plus 2 (0) est égal à 6 (où le 0 est rouge), moins x est égal à 6, x est égal à moins 6, « L'intersection x- est (négatif 6, 0) », « Trouvez l'intersection y-. Soit x égal à 0 », moins x plus 2y est égal à 6, moins 0 plus 2y est égal à 6 (où le 0 est rouge), 2y est égal à 6, y est égal à 3 et « L'intersection y- est (0, 3) ».$ $L'étape 2 de la procédure générale est « Trouver une autre solution à l'équation ». L'étape 2 de l'exemple est une série d'instructions et d'équations : « Nous utiliserons x égal à 2 », « Let x égal à 2 », moins x plus 2y est égal à 6, moins 2 plus 2y est égal à 6 (où les 2 premiers sont rouges), 2y est égal à 8, y est égal à 4 et « Un troisième point est (2, 4) ». L'étape 3 de la procédure générale est la suivante : « Tracez les trois points. Vérifiez que les points s'alignent. 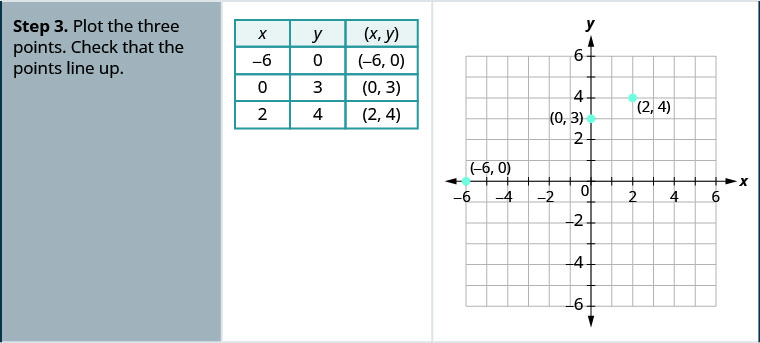»$ $L'étape 3 de l'exemple est un tableau et un graphique. Le tableau comporte quatre lignes et trois colonnes. La première ligne est une ligne d'en-tête et elle étiquette chaque colonne. L'en-tête de la première colonne est « x », le second est « y » et le troisième est « (x, y) ». Sous la première colonne se trouvent les chiffres négatifs 6, 0 et 2. Sous la deuxième colonne se trouvent les chiffres 0, 3 et 4. Sous la troisième colonne se trouvent les paires ordonnées (moins 6, 0), (0, 3) et (2, 4). Le graphique comporte trois points sur le plan de coordonnées x-y. L'axe X du plan va de moins 7 à 7. L'axe y des plans va de moins 7 à 7. 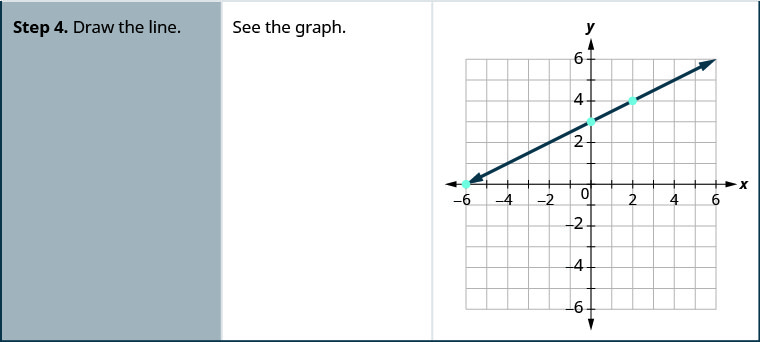Trois points sont marqués à (négatif 6, 0), (0, 3) et (2, 4).$ $L'étape 4 de la procédure générale est « Tracer la ligne ». Pour l'exemple spécifique, il y a l'énoncé « Voir le graphique » et un graphique représentant une ligne droite passant par trois points sur le plan de coordonnées x y. L'axe X du plan va de moins 7 à 7. L'axe y des plans va de moins 7 à 7. Trois points sont marqués à (négatif 6, 0), (0, 3) et (2, 4). La ligne droite passe par les points (négatif 6, 0), (négatif 4, 1), (négatif 2, 2), (0, 3), (2, 4), (4, 5) et (6, 6).$

Exercice$\PageIndex{11}$

Graphe x—2y=4 en utilisant les interceptions.

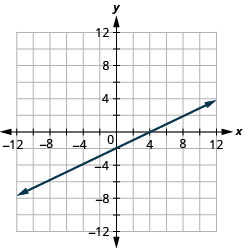
Réponse: $La figure montre une ligne droite sur le plan de coordonnées x y. L'axe X du plan va de moins 12 à 12. L'axe y des plans va de moins 12 à 12. La ligne droite passe par les points (négatif 10, négatif 7), (négatif 8, négatif 6), (négatif 6, négatif 5), (négatif 4, négatif 4), (négatif 2, négatif 3), (0, négatif 2), (2, négatif 1), (4, 0), (6, 1), (8, 2) et (10, 3).$

Exercice$\PageIndex{12}$

Graphe —x+3y=6 en utilisant les interceptions.

Réponse: $La figure montre une ligne droite sur le plan de coordonnées x y. L'axe X du plan va de moins 12 à 12. L'axe y des plans va de moins 12 à 12. La ligne droite passe par les points (négatif 12, moins 2), (négatif 9, négatif 1), (négatif 6, 0), (négatif 3, 1), (0, 2), (3, 3), (6, 4), (9, 5) et (12, 6).$

Les étapes pour représenter graphiquement une équation linéaire à l'aide des interceptions sont résumées ci-dessous.

REPRÉSENTEZ UNE ÉQUATION LINÉAIRE EN UTILISANT LES INTERCEPTS.

Trouvez les points d'intersection x et y de la ligne.
- Soit y = 0 et résolvez pour x
- Soit x=0 et résolvez pour y.
Trouvez une troisième solution à l'équation.
Tracez les trois points et vérifiez qu'ils s'alignent.
Tracez la ligne.

Exercice$\PageIndex{13}$

Graphique 4x—3y=12 en utilisant les interceptions.

Réponse

Trouvez les points d'interception et un troisième point.

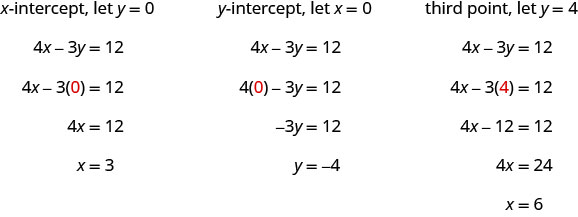
$La figure montre une série d'instructions et d'équations : « Trouvez l'intersection X. Soit y égal à 0 », 4x moins 3y est égal à 12, 4x moins 3 (0) est égal à 12 (où le 0 est rouge), 4x est égal à 12, x est égal à 3, « Trouvez l'intersection y- ». Soit x égal à 0 », 4x moins 3y est égal à 12, 4 (0) moins 3y est égal à 12 (où le 0 est rouge), moins 3y est égal à 12, y est égal à moins 4, « troisième point, soit y égal à 4 », 4x moins 3y est égal à 12, 4x moins 3 (4) est égal à 12 (où le second 4 est rouge), 4x moins 12 est égal à 12, 4x est égal à 24, et x est égal à 6.$

Nous listons les points dans le tableau$\PageIndex{7}$ et montrons le graphique ci-dessous.

4x−3 y=12
x	y	(x, y)
3	0	(3,0)
0	−4	(0, −4)
6	4	(6,4)

Tableau$\PageIndex{7}$

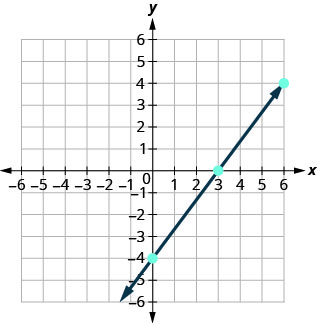
$La figure montre le graphique d'une ligne droite passant par trois points sur le plan de coordonnées x y. L'axe X du plan va de moins 7 à 7. L'axe y des plans va de moins 7 à 7. Trois points sont marqués à (0, moins 4), (3, 0) et (6, 4). La ligne droite passe par les points (0, moins 4), (3, 0) et (6, 4).$

Exercice$\PageIndex{14}$

Graphique 5x—2y=10 en utilisant les interceptions.

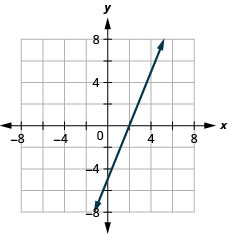
Réponse: $La figure montre le graphique d'une ligne droite sur le plan de coordonnées x y. L'axe X du plan va de moins 7 à 7. L'axe y des plans va de moins 7 à 7. La ligne droite passe par les points (0, moins 5), (2, 0) et (4, 5).$

Exercice$\PageIndex{15}$

Graphique 3x—4y=12 en utilisant les interceptions.

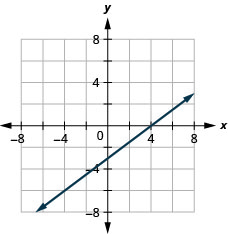
Réponse: $La figure montre le graphique d'une ligne droite sur le plan de coordonnées x y. L'axe X du plan va de moins 7 à 7. L'axe y des plans va de moins 7 à 7. La ligne droite passe par les points (moins 4, moins 6), (0, moins 3) et (4, 0).$

Exercice$\PageIndex{16}$

Graphe y=5x en utilisant les interceptions.

Réponse

$La figure montre deux ensembles d'instructions et d'équations permettant de trouver les interceptions à partir d'une équation. Le premier ensemble d'instructions et d'équations est « x- intercepter », « laisser y égal 0 », y est égal à 5x, 0 est égal à 5x (où le 0 est rouge), 0 est égal à x, (0, 0). Le deuxième ensemble d'instructions et d'équations est « y- intercepter », « laisser x égal à 0 », y est égal à 5x, y est égal à 5 (0) (où le 0 est rouge), y est égal à 0, (0, 0).$

Cette ligne n'a qu'une seule interception. C'est le point (0,0).

Pour garantir la précision, nous devons tracer trois points. Puisque les points d'intersection x et y sont identiques, nous avons besoin de deux points supplémentaires pour tracer la ligne.

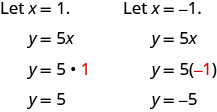
$La figure montre deux ensembles d'énoncés et d'équations permettant de trouver deux points à partir d'une équation. Le premier ensemble d'énoncés et d'équations est « Let x égal à 1 », y est égal à 5x, y est égal à 5 (1) (où le 1 est rouge), y est égal à 5. Le deuxième ensemble d'énoncés et d'équations est « Soit x égal à moins 1 », y est égal à 5x, y est égal à 5 (négatif 1) (où le négatif 1 est rouge), y est égal à moins 5.$

Voir le tableau$\PageIndex{8}$.

y = 5 x
x	y	(x, y)
		(0,0)
		(1,5)
−1	−5	(−1, −5)

Tableau$\PageIndex{8}$

Tracez les trois points, vérifiez qu'ils s'alignent et tracez la ligne.

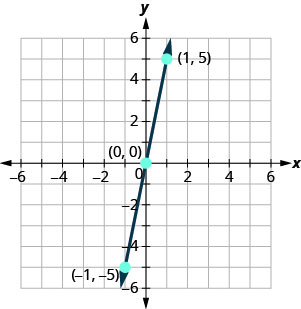
$La figure montre le graphique d'une ligne droite passant par trois points sur le plan de coordonnées x y. L'axe X du plan va de moins 10 à 10. L'axe y des plans va de moins 10 à 10. Trois points sont marqués et étiquetés avec leurs coordonnées à (négatif 1, négatif 5), (0, 0) et (1, 5). La ligne droite passe par les points (moins 1, moins 5), (0, 0) et (1, 5).$

Exercice$\PageIndex{17}$

Graphe y=4x en utilisant les interceptions.

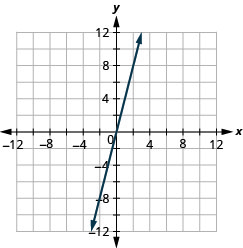
Réponse: $La figure montre une ligne droite sur le plan de coordonnées x y. L'axe X du plan va de moins 12 à 12. L'axe y des plans va de moins 12 à 12. La ligne droite passe par les points (négatif 4, négatif 12), (négatif 3, négatif 9), (négatif 2, négatif 6), (négatif 1, négatif 3), (0, 0), (1, 3), (2, 6), (3, 9) et (4, 12).$

Exercice$\PageIndex{18}$

Tracez y=−x les interceptions.

Réponse: $La figure montre une ligne droite sur le plan de coordonnées x y. L'axe X du plan va de moins 12 à 12. L'axe y des plans va de moins 12 à 12. La ligne droite passe par les points (négatif 10, 10), (négatif 9, 9), (négatif 8, 8), (négatif 7, 7), (négatif 6, 6), (négatif 5, 5), (négatif 4, 4), (négatif 3, 3), (négatif 2, 2), (négatif 1, 1), (0, 0), (1, négatif 1), (2, négatif 2)), (3, négatif 3), (4, négatif 4), (5, négatif 5), (6, négatif 6), (7, négatif 7), (8, négatif 8), (9, négatif 9) et (10, négatif 10).$

Concepts clés

Trouvez les interceptions x et y à partir de l'équation d'une droite
- Utilisez l'équation de la droite pour trouver l'intersection x de la droite, soit y=0 et résolvez pour x.
- Utilisez l'équation de la droite pour trouver l'intersection y - de la droite, soit x=0 et résolvez pour y.
Tracez une équation linéaire à l'aide des interceptions
1. Trouvez les points d'intersection x et y de la ligne.
  Soit y = 0 et résolvez pour x.
  Soit x=0 et résolvez pour y.
2. Trouvez une troisième solution à l'équation.
3. Tracez les trois points, puis vérifiez qu'ils s'alignent.
4. Tracez la ligne.
Stratégie pour choisir la méthode la plus pratique pour tracer une ligne :
- Examinez la forme de l'équation.
- S'il ne comporte qu'une seule variable, il s'agit d'une ligne verticale ou horizontale.
  x=a est une ligne verticale passant par l'axe x - en a
  y=b est une ligne horizontale passant par l'axe y en b.
- Si y est isolé d'un côté de l'équation, tracez un graphique en traçant des points.
- Choisissez trois valeurs quelconques pour x, puis résolvez les valeurs y correspondantes.
- Si l'équation est de la forme ax+by=c, trouvez les points d'intersection. Trouvez les points d'intersection x et y, puis un troisième point.

Lexique

interceptions d'une ligne: Les points où une ligne croise l'axe x et l'axe y sont appelés points d'intersection de la ligne.

x - intercepter: Le point (a,0) où la ligne croise l'axe x ; l'intersection x - se produit lorsque y est égal à zéro.

par -intercept: Le point (0, b) où la ligne croise l'axe y ; l'intersection y se produit lorsque x est nul.

INTERCEPTIONS D'UNE LIGNE

INTERCEPTION X ET INTERCEPTION Y D'UNE LIGNE

Exercice\(\PageIndex{1}\)

Exercice\(\PageIndex{2}\)

Exercice\(\PageIndex{3}\)

X- ET Y - INTERCEPTIONS À PARTIR DE L'ÉQUATION D'UNE DROITE

Exercice\(\PageIndex{4}\)

Exercice\(\PageIndex{5}\)

Exercice\(\PageIndex{6}\)

Exercice\(\PageIndex{7}\)

Exercice\(\PageIndex{8}\)

Exercice\(\PageIndex{9}\)

Exercice\(\PageIndex{10}\): How to Graph a Line Using Intercepts

Exercice\(\PageIndex{11}\)

Exercice\(\PageIndex{12}\)

REPRÉSENTEZ UNE ÉQUATION LINÉAIRE EN UTILISANT LES INTERCEPTS.

Exercice\(\PageIndex{13}\)

Exercice\(\PageIndex{14}\)

Exercice\(\PageIndex{15}\)

Exercice\(\PageIndex{16}\)

Exercice\(\PageIndex{17}\)

Exercice\(\PageIndex{18}\)