Skip to main content
Global

1.9 : Les vrais chiffres

  1. Last updated
  2. Save as PDF
  • Page ID
    195300

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Objectifs d'apprentissage

    À la fin de cette section, vous serez en mesure de :

    • Simplifiez les expressions avec des racines
    • Identifiez les entiers, les nombres rationnels, les nombres irrationnels et les nombres réels
    • Localisez les fractions sur la ligne numérique
    • Localiser les décimales sur la ligne numérique
    Remarque

    Vous trouverez une introduction plus complète aux sujets abordés dans cette section dans les chapitres sur la préalgèbre, Décimaux et propriétés des nombres réels.

    Simplifiez les expressions avec des racines

    N'oubliez pas que lorsqu'un nombre\(n\) est multiplié par lui-même, nous l'écrivons\(n^{2}\) et le lisons «\(n\) au carré ». Le résultat s'appelle le carré de\(n\). Par exemple,

    \[\begin{array} { l l } { 8 ^ { 2 } } & { \text { read '8 squared' } } \\ { 64 } & { 64 \text { is called the square of } 8 \text { . } } \end{array}\]

    De même, 121 est le carré de 11, car\(11^{2}\) c'est 121.

    CARRÉ D'UN CHIFFRE

    Si\(n^{2}=m\), alors\(m\) est le carré de\(n\).

    Remarque

    L'activité de mathématiques manipulatrices « Nombres carrés » vous aidera à mieux comprendre les nombres carrés parfaits.

    Remplissez le tableau suivant pour afficher les carrés des nombres de comptage de 1 à 15.

    Il y a un tableau composé de deux rangées et de 17 colonnes. La première ligne se lit de gauche à droite : Number, n, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14 et 15. La deuxième ligne se lit de gauche à droite : Carré, n au carré, blanc, blanc, blanc, blanc, blanc, blanc, blanc, blanc, blanc, 64, blanc, blanc, blanc, blanc, blanc, blanc, blanc et blanc.
    Figurine\(\PageIndex{1}\)

    Les nombres de la deuxième rangée sont appelés nombres carrés parfaits. Il sera utile d'apprendre à reconnaître les nombres carrés parfaits.

    Les carrés des nombres de comptage sont des nombres positifs. Qu'en est-il des carrés de nombres négatifs ? Nous savons que lorsque les signes de deux nombres sont identiques, leur produit est positif. Ainsi, le carré de tout nombre négatif est également positif.

    \[( - 3 ) ^ { 2 } = 9 \quad ( - 8 ) ^ { 2 } = 64 \quad ( - 11 ) ^ { 2 } = 121 \quad ( - 15 ) ^ { 2 } = 225\]

    Avez-vous remarqué que ces carrés sont identiques aux carrés des nombres positifs ?

    Parfois, nous devrons examiner la relation entre les nombres et leurs carrés à l'envers. Parce\(10^{2}=100\) que nous disons que 100 est le carré de 10. Nous disons également que 10 est une racine carrée de 100. Un nombre dont le carré est mm est appelé racine carrée de\(m\).

    RACINE CARRÉE D'UN NOMBRE

    Si\(n^{2}=m\), alors\(n\) est une racine carrée de\(m\).

    Remarquez\((−10)^{2}=100\) également qu'il en\(−10\) va de même pour la racine carrée de\(100\). Par conséquent, les deux\(10\) et\(−10\) sont des racines carrées de\(100\).

    Ainsi, chaque nombre positif a deux racines carrées : une positive et une négative. Et si nous ne voulions que la racine carrée positive d'un nombre positif ? Le signe radical,\(\sqrt{m}\), indique la racine carrée positive. La racine carrée positive est appelée racine carrée principale. Lorsque nous utilisons le signe radical, cela signifie toujours que nous voulons la racine carrée principale.

    Nous utilisons également le signe radical pour la racine carrée de zéro. Parce que\(0^{2}=0, \sqrt{0}=0\). Notez que zéro n'a qu'une seule racine carrée.

    NOTATION À RACINES CARRÉES

    \(\sqrt{m}\)est lu « la racine carrée de\(m\) »

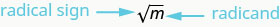
    Une racine carrée est donnée, avec une flèche pointant vers le signe radical (cela ressemble à une coche avec une ligne horizontale partant de son extrémité longue) indiquant le signe radical et une flèche pointant vers le chiffre situé sous le signe radical, qui est marqué radical.

    Si\(m = n^{2}\), alors\(\sqrt{m} = n\), pour\(n\geq 0\).

    La racine carrée de\(m\)\(\sqrt{m}\), est le nombre positif dont le carré est\(m\).

    Puisque 10 est la racine carrée principale de 100, nous écrivons\(\sqrt{100}=10\). Vous pouvez remplir le tableau suivant pour vous aider à reconnaître les racines carrées.

    Il y a un tableau à deux rangées et 15 colonnes. La première rangée se lit de gauche à droite comme suit : racine carrée de 1, racine carrée de 4, racine carrée de 9, racine carrée de 16, racine carrée de 25, racine carrée de 36, racine carrée de 49, racine carrée de 64, racine carrée de 81, racine carrée de 100, racine carrée de 121, racine carrée de 144, racine carrée de 169, racine carrée de 196, et racine carrée de 225. La deuxième ligne comprend tous les espaces, à l'exception de la dixième cellule située sous la racine carrée de 100, qui indique 10.
    Figurine\(\PageIndex{2}\)
    Exercice\(\PageIndex{1}\)

    Simplifiez :

    1. \(\sqrt{25}\)
    2. \(\sqrt{121}\)
    Réponse
    1. \[\begin{array} {ll} {} &{\sqrt{25}} \\ {\text {Since }5^{2} = 25} &{5} \end{array}\]
    2. \[\begin{array} {ll} {} &{\sqrt{121}} \\ {\text {Since }11^{2} = 121} &{11} \end{array}\]
    Exercice\(\PageIndex{2}\)

    Simplifiez :

    1. \(\sqrt{36}\)
    2. \(\sqrt{169}\)
    Réponse
    1. 6
    2. 13
    Exercice\(\PageIndex{3}\)

    Simplifiez :

    1. \(\sqrt{16}\)
    2. \(\sqrt{196}\)
    Réponse
    1. 4
    2. 14

    Nous savons que chaque nombre positif a deux racines carrées et que le signe radical indique la racine positive. Nous écrivons\(\sqrt{100)=10\). Si nous voulons trouver la racine carrée négative d'un nombre, nous plaçons un négatif devant le signe radical. Par exemple,\(-\sqrt{100)=-10\). Nous nous lisons\(-\sqrt{100)\) comme « l'opposé de la racine carrée de 10 ».

    Exercice\(\PageIndex{4}\)

    Simplifiez :

    1. \(-\sqrt{9}\)
    2. \(-\sqrt{144}\)
    Réponse
    1. \[\begin{array} {ll} {} &{-\sqrt{9}} \\ {\text {The negative is in front of the radical sign.}} &{-3} \end{array}\]
    2. \[\begin{array} {ll} {} &{-\sqrt{144}} \\ {\text {The negative is in front of the radical sign.}} &{-12} \end{array}\]
    Exercice\(\PageIndex{5}\)

    Simplifiez :

    1. \(\sqrt{16}\)
    2. \(\sqrt{196}\)
    Réponse
    1. −2
    2. −15
    Exercice\(\PageIndex{6}\)

    Simplifiez :

    1. \(\sqrt{16}\)
    2. \(\sqrt{196}\)
    Réponse
    1. −9
    2. −10

    Identifier les entiers, les nombres rationnels, les nombres irrationnels et les nombres réels

    Nous avons déjà décrit les nombres comme comptant le nombre s, le nombre entier s et les entiers. Quelle est la différence entre ces types de chiffres ?

    \[\begin{array} { l l } { \text { Counting numbers } } & { 1,2,3,4 , \ldots } \\ { \text { Whole numbers } } & { 0,1,2,3,4 , \ldots } \\ { \text { Integers } } & { \dots - 3 , - 2 , - 1,0,1,2,3 , \ldots } \end{array}\]

    Quel type de nombres obtiendrions-nous si nous commencions par tous les entiers et que nous incluions ensuite toutes les fractions ? Les nombres que nous aurions forment l'ensemble des nombres rationnels. Un nombre rationnel est un nombre qui peut être écrit sous la forme d'un ratio de deux entiers.

    NUMÉRO RATIONNEL

    Un nombre rationnel est un nombre de la forme\(\dfrac{p}{q}\), où p et q sont des nombres entiers et\(q \neq 0\)

    Un nombre rationnel peut être écrit comme le ratio de deux entiers.

    Toutes les fractions signées, telles que\(\dfrac{4}{5}\),\(-\dfrac{7}{8}\),\(\dfrac{13}{4}\),\(-\dfrac{20}{3}\) sont des nombres rationnels. Chaque numérateur et chaque dénominateur sont des nombres entiers.

    Les entiers sont-ils des nombres rationnels ? Pour décider si un entier est un nombre rationnel, nous essayons de l'écrire sous la forme d'un ratio de deux entiers. Chaque entier peut être écrit sous forme de ratio d'entiers de nombreuses manières. Par exemple, 3 est équivalent à\(\dfrac{3}{1}\),\(-\dfrac{6}{2}\),\(\dfrac{9}{3}\),\(\dfrac{12}{4}\),\(-\dfrac{15}{5} \ldots\)

    Un moyen simple d'écrire un entier sous forme de ratio d'entiers est de l'écrire sous forme de fraction avec le dénominateur un.

    \[3 = \frac { 3 } { 1 } \quad - 8 = - \frac { 8 } { 1 } \quad 0 = \frac { 0 } { 1 }\]

    Comme tout entier peut être écrit comme le ratio de deux entiers, tous les entiers sont des nombres rationnels ! N'oubliez pas que les nombres de comptage et les nombres entiers sont également des nombres entiers et qu'ils sont donc également rationnels.

    Qu'en est-il des décimales ? Sont-ils rationnels ? Examinons quelques-uns pour voir si nous pouvons écrire chacun d'eux comme le ratio de deux entiers.

    Nous avons déjà vu que les entiers sont des nombres rationnels. L'entier\(−8\) peut être écrit sous forme décimale\(−8.0\). Il est donc clair que certaines décimales sont rationnelles.

    Pense à la décimale\(7.3\). Pouvons-nous l'écrire comme un ratio de deux entiers ? Parce que\(7.3\) cela signifie\(7\dfrac{3}{10}\) que nous pouvons l'écrire comme une fraction impropre,\(\dfrac{73}{10}\). Il en\(7.3\) va de même pour le ratio des nombres entiers\(73\) et\(10\). C'est un chiffre rationnel.

    En général, toute décimale qui se termine après un certain nombre de chiffres (par exemple,\(7.3\) ou\(−1.2684\)) est un nombre rationnel. Nous pouvons utiliser la valeur de position du dernier chiffre comme dénominateur lors de l'écriture de la décimale sous forme de fraction.

    Exercice\(\PageIndex{7}\)

    Écrivez comme le ratio de deux entiers :

    1. −27
    2. 7,31
    Réponse
    1. \[\begin{array} {ll} {} &{-27} \\ {\text {Write it as a fraction with denominator 1.}} &{\dfrac{-27}{1}} \end{array}\]
    2. \[\begin{array} {ll} {} &{7.31} \\ {\text {Write is as a mixed number. Remember.}} &{} \\ {\text {7 is the whole number and the decimal}} &{7\dfrac{31}{100}} \\ {\text {part, 0.31, indicates hundredths.}} &{} \\ {\text{Convert to an improper fraction.}} &{\dfrac{731}{100}} \end{array}\]

    Nous voyons donc que −27 et 7,31 sont tous deux des nombres rationnels, puisqu'ils peuvent être écrits comme le ratio de deux entiers.

    Exercice\(\PageIndex{8}\)

    Écrivez comme le ratio de deux entiers :

    1. −24
    2. 3,57
    Réponse
    1. \(\dfrac{-24}{1}\)
    2. \(\dfrac{357}{100}\)
    Exercice\(\PageIndex{9}\)

    Écrivez comme le ratio de deux entiers :

    1. −19
    2. 8,41
    Réponse
    1. \(\dfrac{-19}{1}\)
    2. \(\dfrac{841}{100}\)
    Regardons la forme décimale des nombres dont nous savons qu'ils sont rationnels.

    Nous avons vu que chaque entier est un nombre rationnel, puisque\(a = \dfrac{a}{1}\) pour tout entier,\(a\). Nous pouvons également changer n'importe quel entier en décimal en ajoutant un point décimal et un zéro.

    \[\begin{array} { l l l l l l l } { \text { Integer } } & { - 2 } & { - 1 } & { 0 } & { 1 } & { 2 } & { 3 } \\ { \text { Decimal form } } & { - 2.0 } & { - 1.0 } & { 0.0 } & { 1.0 } & { 2.0 } & { 3.0 } \\ { } & { \text { These decimal numbers stop. } } \end{array}\]

    Nous avons également vu que chaque fraction est un nombre rationnel. Regardez la forme décimale des fractions que nous avons considérées ci-dessus.

    \[\begin{array} { l l l l } { \text { Ratio of integers } } & { \frac { 4 } { 5 } } & { - \frac { 7 } { 8 } } & { \frac { 13 } { 4 } } & { - \frac { 20 } { 3 } } \\ { \text { The decimal form } } & { 0.8 } & { - 0.875 } & { 3.25 } & { - 6.666 \dots } \\ { } & { } & { } & { - 6.\overline{6} } \\ { } & { \text { These decimal either stop or repeat. } } \end{array}\]

    Que nous apprennent ces exemples ?

    Chaque nombre rationnel peut être écrit à la fois sous la forme d'un ratio d'entiers\(\dfrac{p}{q}\), (, où p et q sont des nombres entiers et\(q\neq 0\)), et sous la forme d'une décimale qui s'arrête ou se répète.

    Voici les nombres que nous avons examinés ci-dessus exprimés sous forme de ratio d'entiers et de décimales :

    Fractions Entiers
    Numéro \(\frac{4}{5}\) \(\frac{7}{8}\) \(\frac{13}{4}\) \(-\frac{20}{3}\) −2 −1 0 1 2 3
    Ratio de nombres entiers \(\frac{4}{5}\) \(\frac{7}{8}\) \(\frac{13}{4}\) \(-\frac{20}{3}\) \(-\frac{2}{1}\) \(-\frac{1}{1}\) \(\frac{0}{1}\) \(\frac{1}{1}\) \(\frac{2}{1}\) \(\frac{3}{1}\)
    Forme décimale 0,8 −0,875 3,25 \(−6.\overline{6}\) −2,0 −1,0 0,0 1,0 2,0 3,0
    Tableau\(\PageIndex{1}\)
    NUMÉRO RATIONNEL

    Un nombre rationnel est un nombre de la forme\(\frac{p}{q}\), où p et q sont des nombres entiers et\(q\neq 0\)

    Sa forme décimale s'arrête ou se répète.

    Y a-t-il des décimales qui ne s'arrêtent pas ou ne se répètent pas ? Oui !

    Le nombre\(\pi\) (la lettre grecque pi, prononcée « pie »), qui est très important pour décrire les cercles, a une forme décimale qui ne s'arrête pas et ne se répète pas.

    \[\pi =3.141592654\ldots\]

    Nous pouvons même créer un schéma décimal qui ne s'arrête pas et ne se répète pas, tel que

    \[2.01001000100001\ldots\]

    Les nombres dont la forme décimale ne s'arrête pas ou ne se répète pas ne peuvent pas être écrits sous forme de fraction d'entiers. Nous disons que ces chiffres sont irrationnels.

    NOMBRE IRRATIONNEL

    Un nombre irrationnel est un nombre qui ne peut pas être écrit comme le ratio de deux entiers.

    Sa forme décimale ne s'arrête pas et ne se répète pas.

    Résumons une méthode que nous pouvons utiliser pour déterminer si un nombre est rationnel ou irrationnel.

    RATIONNEL OU IRRATIF ?

    Si la forme décimale d'un nombre

    • se répète ou s'arrête, le nombre est rationnel.
    • ne se répète pas et ne s'arrête pas, le nombre est irrationnel.
    Exercice\(\PageIndex{10}\)

    Compte tenu de la\(0.58\overline{3}, 0.47, 3.605551275\ldots\) liste des numéros

    1. nombres rationnels
    2. nombres irrationnels.
    Réponse
    1. \[\begin{array} {ll} {\text{Look for decimals that repeat or stop}} &{\text{The 3 repeats in }0.58\overline{3}.} \\ {} &{\text {The decimal 0.47 stops after the 7.}}\\ {} &{\text {So } 0.58\overline{3} \text{ and } 0.47 \text{are rational}} \end{array}\]
    2. \[\begin{array} {ll} {\text{Look for decimals that repeat or stop}} &{3.605551275\ldots\text{has no repeating block of}} \\ {} &{\text {digits and it does not stop.}}\\ {} &{\text {So } 3.605551275\ldots \text{ is irrational.}} \end{array}\]
    Exercice\(\PageIndex{11}\)

    Pour les numéros donnés, listez les

    1. nombres rationnels
    2. nombres irrationnels :\(0.29, 0.81\overline{6}, 2.515115111….\)
    Réponse
    1. \(0.29, 0.81\overline{6}\)
    2. \(2.515115111….\)
    Exercice\(\PageIndex{12}\)

    Pour les numéros donnés, listez les

    1. nombres rationnels
    2. nombres irrationnels :\(2.6\overline{3}, 0.125, 0.418302…\)
    Réponse
    1. \(2.6\overline{3}, 0.125\)
    2. \(0.418302…\)
    Exercice\(\PageIndex{13}\)

    Pour chaque chiffre donné, déterminez s'il est rationnel ou irrationnel :

    1. \(\sqrt{36}\)
    2. \(\sqrt{44}\)
    Réponse
    1. Reconnaissez que 36 est un carré parfait, puisque\(6^{2} = 36\). Donc\(\sqrt{36} = 6\),\(\sqrt{36}\) c'est rationnel.
    2. N'oubliez pas que\(6^{2} = 36\) ce n'\(44\)est pas un carré parfait.\(7^{2} = 49\) Par conséquent, la forme décimale de ne se\(\sqrt{44}\) répétera jamais et ne s'arrêtera jamais,\(\sqrt{44}\) elle est donc irrationnelle.
    Exercice\(\PageIndex{14}\)

    Pour chaque chiffre donné, déterminez s'il est rationnel ou irrationnel :

    1. \(\sqrt{81}\)
    2. \(\sqrt{17}\)
    Réponse
    1. rationnel
    2. irrationnel
    Exercice\(\PageIndex{15}\)

    Pour chaque chiffre donné, déterminez s'il est rationnel ou irrationnel :

    1. \(\sqrt{116}\)
    2. \(\sqrt{121}\)
    Réponse
    1. irrationnel
    2. rationnel

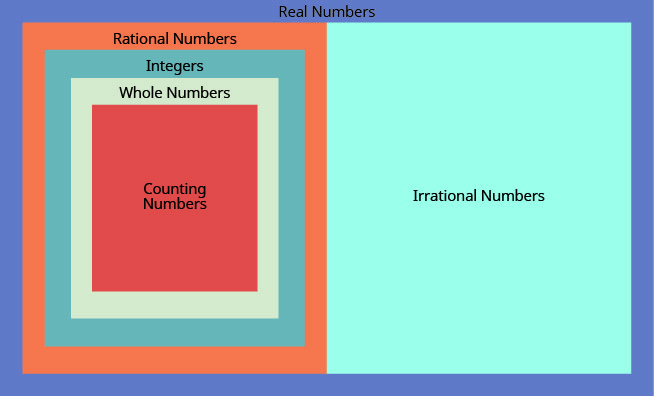
    Nous avons vu que tous les nombres de comptage sont des nombres entiers, que tous les nombres entiers sont des entiers et que tous les nombres entiers sont des nombres rationnels. Les nombres irrationnels sont des nombres dont la forme décimale ne s'arrête pas et ne se répète pas. Lorsque nous réunissons les nombres rationnels et les nombres irrationnels, nous obtenons l'ensemble des nombres réels s.

    NUMÉRO RÉEL

    Un nombre réel est un nombre rationnel ou irrationnel.

    Tous les nombres que nous utilisons en algèbre élémentaire sont des nombres réels. La figure\(\PageIndex{3}\) montre comment les ensembles de numéros dont nous avons parlé dans cette section s'imbriquent.

    Cette figure consiste en un diagramme de Venn. Pour commencer, il y a un grand rectangle marqué Nombres réels. La moitié droite du rectangle est constituée de nombres irrationnels. La moitié gauche est constituée de nombres rationnels. Dans le rectangle des nombres rationnels, il y a des entiers..., moins 2, moins 1, 0, 1, 2,... Dans le rectangle des entiers, il y a des nombres entiers 0, 1, 2, 3,... Dans le rectangle des nombres entiers, il y a des nombres de comptage 1, 2, 3,...
    Figure\(\PageIndex{3}\) : Ce graphique montre les ensembles de nombres qui constituent l'ensemble des nombres réels. Le terme « nombres réels » vous semble étrange ? Y a-t-il des chiffres qui ne sont pas « réels » et, dans l'affirmative, quels pourraient-ils être ?

    Pouvons-nous simplifier\(\sqrt{-25}\) ? Y a-t-il un nombre dont le carré est\(−25\) ?

    \[(\quad)^{2}=−25?\]

    Aucun des chiffres que nous avons traités jusqu'à présent n'a de carré\(−25\). Pourquoi ? Tout nombre positif au carré est positif. Tout nombre négatif au carré est positif. Nous disons donc qu'il n'y a pas de nombre réel égal à\(\sqrt{-25}\).

    La racine carrée d'un nombre négatif n'est pas un nombre réel.

    Exercice\(\PageIndex{16}\)

    Pour chaque nombre donné, déterminez s'il s'agit d'un nombre réel ou non :

    1. \(\sqrt{-169}\)
    2. \(-\sqrt{64}\)
    Réponse
    1. Il n'y a pas de nombre réel dont le carré est\(−169\). \(\sqrt{-169}\)Ce n'est donc pas un nombre réel.
    2. Puisque le négatif est devant le radical,\(-\sqrt{64}\) c'est\(−8\), puisque c'\(−8\)est un nombre réel,\(-\sqrt{64}\) c'est un nombre réel.
    Exercice\(\PageIndex{17}\)

    Pour chaque nombre donné, déterminez s'il s'agit d'un nombre réel ou non :

    1. \(\sqrt{-196}\)
    2. \(-\sqrt{81}\)
    Réponse
    1. ce n'est pas un vrai chiffre
    2. nombre réel
    Exercice\(\PageIndex{18}\)

    Pour chaque nombre donné, déterminez s'il s'agit d'un nombre réel ou non :

    1. \(-\sqrt{49}\)
    2. \(\sqrt{-121}\)
    Réponse
    1. nombre réel
    2. ce n'est pas un vrai chiffre
    Exercice\(\PageIndex{19}\)

    Compte tenu des chiffres\(−7, \frac{14}{5}, 8, \sqrt{5}, 5.9, \sqrt{64}\), énumérez les

    1. nombres entiers
    2. entiers
    3. nombres rationnels
    4. nombres irrationnels
    5. nombres réels
    Réponse
    1. N'oubliez pas que les nombres entiers sont 0, 1, 2, 3,... et 8 est le seul nombre entier donné.
    2. Les entiers sont les nombres entiers, leurs contraires et 0. Donc, le nombre entier 8 est un entier, et −7 est l'opposé d'un nombre entier, donc c'est aussi un entier. Notez également que 64 est le carré de 8 donc\(-\sqrt{64} = -8\). Donc, les nombres entiers le sont\(−7, 8, \sqrt{64}\).
    3. Puisque tous les entiers sont rationnels, ils\(-7, 8, -\sqrt{64}\) sont rationnels. Les nombres rationnels incluent également les fractions et les décimales qui se répètent ou s'arrêtent, donc\(\frac{14}{5}\) et\(5.9\) sont rationnels. Donc, la liste des nombres rationnels est\(−7, \frac{14}{5}, 8, 5.9, \sqrt{64}\)
    4. N'oubliez pas que 5 n'est pas un carré parfait, il\(\sqrt{5}\) est donc irrationnel.
    5. Tous les nombres listés sont des nombres réels.
    Exercice\(\PageIndex{20}\)

    Pour les numéros donnés, listez les

    1. nombres entiers
    2. entiers
    3. nombres rationnels
    4. nombres irrationnels
    5. nombres réels :\(−3, -\sqrt{2}, 0.\overline{3}, \frac{9}{5}, 4, \sqrt{49}\)
    Réponse
    1. \(4, \sqrt{49}\).
    2. \(−3, 4, \sqrt{49}\)
    3. \(−3, 0.\overline{3}, \frac{9}{5}, 4, \sqrt{49}\)
    4. \( -\sqrt{2}\)
    5. \(−3, \sqrt{2}, 0.\overline{3}, \frac{9}{5}, 4, \sqrt{49}\)
    Exercice\(\PageIndex{21}\)

    Pour les numéros donnés, listez les

    1. nombres entiers
    2. entiers
    3. nombres rationnels
    4. nombres irrationnels
    5. nombres réels :\(−\sqrt{25},−\frac{3}{8}, −1, 6, \sqrt{121}, 2.041975…\)
    Réponse
    1. \(6, \sqrt{121}\).
    2. \(−\sqrt{25}, −1, 6, \sqrt{121}\)
    3. \(−\sqrt{25},−\frac{3}{8}, −1, 6, \sqrt{121}\)
    4. \(2.041975…\)
    5. \(−\sqrt{25},−\frac{3}{8}, −1, 6, \sqrt{121}, 2.041975…\)

    Localiser les fractions sur la droite numérique

    La dernière fois que nous avons examiné la ligne numérique, elle ne contenait que des entiers positifs et négatifs. Nous voulons maintenant y inclure des fractions s et des décimales.

    Remarque

    L'activité Mathématiques manipulatrices « Ligne numérique, partie 3 » vous aidera à mieux comprendre l'emplacement des fractions sur la droite numérique.

    Commençons par les fractions et localisons\(\frac{1}{5}, -\frac{4}{5}, 3, \frac{7}{4}, -\frac{9}{2}, -5\) et\(\frac{8}{3}\) sur la ligne numérique.

    Nous allons commencer par les nombres entiers 3 et −5, car ce sont les plus faciles à tracer. Voir la figure\(\PageIndex{4}\).

    Les fractions appropriées répertoriées sont\(\frac{1}{5}\text{ and } -\frac{4}{5}\). Nous savons que la fraction appropriée\(\frac{1}{5}\) a une valeur inférieure à un et qu'elle se situerait donc entre 0 et 1. Le dénominateur est 5, nous divisons donc l'unité de 0 à 1 en 5 parties égales\(\frac{1}{5}, \frac{2}{5}, \frac{3}{5}, \frac{4}{5}\). Nous complotons\(\frac{1}{5}\). Voir la figure\(\PageIndex{4}\).

    De même,\(-\frac{4}{5}\) est compris entre 0 et -1. Après avoir divisé l'unité en 5 parties égales, nous tracons\(-\frac{4}{5}\). Voir la figure\(\PageIndex{4}\).

    Enfin, examinez les fractions inappropriées\(\frac{7}{4}, -\frac{9}{2}, \frac{8}{3}\). Il s'agit de fractions dans lesquelles le numérateur est supérieur au dénominateur. Il peut être plus facile de localiser ces points si vous remplacez chacun d'eux par un nombre mixte. Voir la figure\(\PageIndex{4}\).

    \[\frac { 7 } { 4 } = 1 \frac { 3 } { 4 } \quad - \frac { 9 } { 2 } = - 4 \frac { 1 } { 2 } \quad \frac { 8 } { 3 } = 2 \frac { 2 } { 3 }\]

    La figure\(\PageIndex{4}\) montre la ligne numérique avec tous les points tracés.

    Une ligne numérique s'affiche qui va de moins 6 à 6 positif. De gauche à droite, les nombres marqués sont moins 5, moins 9/2, moins 4/5, 1/5, 4/5, 8/3 et 3. Le nombre négatif 9/2 se situe à mi-chemin entre moins 5 et moins 4. Le chiffre négatif 4/5 se trouve légèrement à droite du chiffre négatif 1. Le chiffre 1/5 est légèrement à droite de 0. Le chiffre 4/5 est légèrement à gauche de 1. Le chiffre 8/3 se situe entre 2 et 3, mais un peu plus proche de 3.
    Figurine\(\PageIndex{4}\)
    Exercice\(\PageIndex{22}\)

    Localisez et étiquetez les éléments suivants sur une ligne numérique :\(4, \frac{3}{4}, -\frac{1}{4}, -3, \frac{6}{5}, -\frac{5}{2}\) et\(\frac{7}{3}\).

    Réponse

    Localisez et tracez les nombres entiers, 4, −3.

    Trouvez d'\(\frac{3}{4}\)abord la fraction appropriée. La fraction\(\frac{3}{4}\) est comprise entre 0 et 1. Divisez la distance entre 0 et 1 en quatre parties égales, puis nous tracons\(\frac{3}{4}\). Diagramme similaire\(-\frac{1}{4}\).

    Localisez maintenant les fractions inappropriées\(\frac{6}{5}\),\(-\frac{5}{2}\),\(\frac{7}{3}\). Il est plus facile de les tracer si nous les convertissons en nombres mixtes, puis les traçons comme décrit ci-dessus :\(\frac{6}{5} = 1\frac{1}{5}\),\(-\frac{5}{2} = -2\frac{1}{2}\),\(\frac{7}{3} = 2\frac{1}{3}\).

    Une ligne numérique s'affiche qui va de moins 6 à 6 positif. De gauche à droite, les nombres marqués sont moins 3, moins 5/2, moins 1/4, 3/4, 6/5, 7/3 et 4. Le nombre négatif 5/2 est à mi-chemin entre moins 3 et moins 2. Le nombre moins 1/4 se trouve légèrement à gauche de 0. Le chiffre 3/4 est légèrement à gauche de 1. Le chiffre 6/5 est légèrement à droite de 1. Le chiffre 7/3 est compris entre 2 et 3, mais un peu plus proche de 2.

    Exercice\(\PageIndex{23}\)

    Localisez et étiquetez les éléments suivants sur une ligne numérique :\(-1, \frac{1}{3}, \frac{6}{5}, -\frac{7}{4}, \frac{9}{2}, 5\) et\(-\frac{8}{3}\).

    Réponse

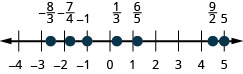
    Une ligne numérique s'affiche, qui va du négatif 4 au positif 5. De gauche à droite, les nombres marqués sont négatifs 8/3, moins 7/4, moins 1, 1/3, 6/5, 9/2 et 5. Le nombre négatif 8/3 se situe entre moins 3 et moins 2 mais légèrement plus proche de moins 3. Le chiffre négatif 7/4 se trouve légèrement à droite du chiffre négatif 2. Le chiffre 1/3 est légèrement à droite de 0. Le chiffre 6/5 est légèrement à droite de 1. Le chiffre 9/2 se situe à mi-chemin entre 4 et 5.

    Exercice\(\PageIndex{24}\)

    Localisez et étiquetez les éléments suivants sur une ligne numérique :\(\frac{1}{5}, -\frac{4}{5}, 3, \frac{7}{4}, -\frac{9}{2}, -5\) et\(\frac{8}{3}\).

    Réponse

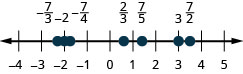
    Une ligne numérique s'affiche, qui va du négatif 4 au positif 5. De gauche à droite, les nombres marqués sont négatifs 7/3, moins 2, moins 7/4, 2/3, 7/5, 3 et 7/2. Le nombre négatif 7/3 se situe entre moins 3 et moins 2 mais légèrement plus proche de moins 2. Le chiffre négatif 7/4 se trouve légèrement à droite du chiffre négatif 2. Le chiffre 2/3 est légèrement à gauche de 1. Le chiffre 7/5 est compris entre 1 et 2, mais plus proche de 1. Le chiffre 7/2 se situe à mi-chemin entre 3 et 4.

    Dans l'exercice\(\PageIndex{25}\), nous utiliserons les symboles d'inégalité pour classer les fractions. Dans les chapitres précédents, nous avons utilisé la ligne numérique pour classer les numéros.

    • \(a < b\)« a est inférieur à b » lorsque a se trouve à gauche de b sur la ligne numérique
    • \(a > b\)« a est supérieur à b » lorsque a se trouve à droite de b sur la ligne numérique

    Lorsque nous nous déplaçons de gauche à droite sur une ligne numérique, les valeurs augmentent.

    Exercice\(\PageIndex{25}\)

    Classez chacune des paires de nombres suivantes, en utilisant\(<\) ou\(>\). Il peut être utile de se référer à la figure\(\PageIndex{5}\).

    1. \(−\frac{2}{3}\text{___}-1\)
    2. \(−3\frac{1}{2}\text{___}-3\)
    3. \(−\frac{3}{4}\text{___}-\frac{1}{4}\)
    4. \(−2\text{___}-\frac{8}{3}\)
    Une ligne numérique s'affiche, qui va du négatif 4 au positif 4. De gauche à droite, les nombres marqués sont moins 3 et 1/2, moins 3, moins 8/3, moins 8/3, moins 2, moins 1, moins 3/4, moins 2/3 et moins 1/4. Le nombre négatif 3 et 1/2 est compris entre moins 4 et moins 3. Le nombre négatif 8/3 est compris entre moins 3 et moins 2, mais plus proche de moins 3. Les nombres négatifs 3/4, moins 2/3 et moins 1/4 sont tous compris entre moins 1 et 0.
    Figurine\(\PageIndex{5}\)
    Réponse

    Soyez prudent lorsque vous commandez des nombres négatifs.

    1. \(\begin{array} { r r } { } & { - \frac { 2 } { 3 } \text{ ___ } -1 } \\ { - \frac { 2 } { 3 } \text { is to the right of } - 1 \text { on the number line. } } & { - \frac { 2 } { 3 } > - 1 } \end{array}\)
    2. \(\begin{array} { r r } { } & { - 3\frac { 1 } { 2 } \text{ ___ } -3 } \\ { - 3\frac { 1 } { 2 } \text { is to the right of } - 3 \text { on the number line. } } & { - \frac { 2 } { 3 } > - 1 } \end{array}\)
    3. \(\begin{array} { r r } { } & { - \frac { 3 } { 4 } \text{ ___ } -\frac{1}{4} } \\ { - \frac { 3 } { 4 } \text { is to the right of } - \frac{1}{4} \text { on the number line. } } & { - \frac{3}{4} < - \frac{1}{4} } \end{array}\)
    4. \(\begin{array} { r r } { } & { - \-2 \text{ ___ } -\frac{8}{3} } \\ { -2 \text { is to the right of } - \frac{8}{3} \text { on the number line. } } & { -2 > -\frac{8}{3} } \end{array}\)
    Exercice\(\PageIndex{26}\)

    Classez chacune des paires de nombres suivantes, en utilisant\(<\) ou\(>\).

    1. \(−\frac{1}{3}\text{___}-1\)
    2. \(−1\frac{1}{2}\text{___}-2\)
    3. \(−\frac{2}{3}\text{___}-\frac{1}{3}\)
    4. \(−3\text{___}-\frac{7}{3}\)
    Réponse
    1. \(>\)
    2. \(>\)
    3. \(<\)
    4. \(<\)
    Exercice\(\PageIndex{27}\)

    Classez chacune des paires de nombres suivantes, en utilisant\(<\) ou\(>\).

    1. \(−1\text{___}-\frac{2}{3}\)
    2. \(−2\frac{1}{4}\text{___}-2\)
    3. \(−\frac{3}{5}\text{___}-\frac{4}{5}\)
    4. \(−4\text{___}-\frac{10}{3}\)
    Réponse
    1. \(<\)
    2. \(<\)
    3. \(>\)
    4. \(<\)

    Localiser les décimales sur la ligne numérique

    Les décimales étant des formes de fractions, la localisation des décimales sur la ligne numérique est similaire à la localisation des fractions sur la ligne numérique.

    Exercice\(\PageIndex{28}\)

    Localisez 0,4 sur la ligne numérique.

    Réponse

    Une fraction appropriée a une valeur inférieure à un. Le nombre décimal\(0.4\) est équivalent à\(\frac{4}{10}\) une fraction propre et se\(0.4\) situe donc entre 0 et 1. Sur une ligne numérique, divisez l'intervalle entre 0 et 1 en 10 parties égales. Maintenant, étiquetez les pièces\(0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0\). Nous écrivons 0 comme 0,0 et 1 et 1,0, de sorte que les nombres soient toujours en dixièmes. Enfin, marquez\(0.4\) sur la ligne numérique. Voir la figure\(\PageIndex{6}\).

    Une ligne numérique s'affiche entre 0,0 et 1. Le seul point indiqué est 0,4, soit entre 0,3 et 0,5.
    Figurine\(\PageIndex{6}\)
    Exercice\(\PageIndex{29}\)

    Localisez sur la ligne numérique : 0,6.

    Réponse

    Une ligne numérique s'affiche entre 0,0 et 1. Le seul point indiqué est 0,6, soit entre 0,5 et 0,7.

    Exercice\(\PageIndex{30}\)

    Localisez sur la ligne numérique : 0,9.

    Réponse

    Une ligne numérique s'affiche entre 0,0 et 1. Le seul point indiqué est 0,9, soit entre 0,8 et 1.

    Exercice\(\PageIndex{31}\)

    Localisez\(−0.74\) sur la ligne numérique.

    Réponse

    La décimale (−0,74 \) est équivalente à\(-\frac{74}{100}\), elle est donc située entre 0 et −1. Sur une ligne numérique, cochez et étiquetez les centièmes de l'intervalle compris entre 0 et −1. Voir la figure\(\PageIndex{7}\).

    Une ligne numérique s'affiche, allant de moins 1,00 à 0,00. Le seul point indiqué est négatif 0,74, qui se situe entre moins 0,8 et moins 0,7.
    Figurine\(\PageIndex{7}\)
    Exercice\(\PageIndex{32}\)

    Localisez sur la ligne numérique : −0,6.

    Réponse

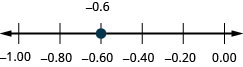
    Une ligne numérique s'affiche, allant de moins 1,00 à 0,00. Le seul point indiqué est négatif 0,6, qui se situe entre moins 0,8 et moins 0,4.

    Exercice\(\PageIndex{33}\)

    Localisez sur la ligne numérique : −0,7.

    Réponse

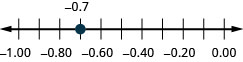
    Une ligne numérique s'affiche, allant de moins 1,00 à 0,00. Le seul point indiqué est négatif 0,7, qui se situe entre moins 0,8 et moins 0,6.

    Lequel est le plus grand, 0,04 ou 0,40 ? Si vous considérez cela comme de l'argent, vous savez que 0,40$ (quarante cents) est supérieur à 0,04$ (quatre cents). Donc,\(0.40 > 0.04\)

    Encore une fois, nous pouvons utiliser la ligne numérique pour commander des numéros.

    • \(a < b\)« a est inférieur à b » lorsque a se trouve à gauche de b sur la ligne numérique
    • \(a > b\)« a est supérieur à b » lorsque a se trouve à droite de b sur la ligne numérique

    Où se situent 0.04 et 0.40 sur la ligne numérique ? Voir la figure\(\PageIndex{8}\).

    Une ligne numérique s'affiche entre 0,0 et 1,0. De gauche à droite, les points 0,04 et 0,4 sont marqués. Le point 0,04 est compris entre 0,0 et 0,1. Le point 0,4 est compris entre 0,3 et 0,5.
    Figurine\(\PageIndex{8}\)

    Nous voyons que 0,40 est à droite de 0,04 sur la ligne numérique. C'est une autre façon de le démontrer\(0.40 > 0.04\).

    Comment se compare 0,31 à 0,308 ? Cela ne se traduit pas par de l'argent pour faciliter la comparaison. Mais si nous convertissons 0,31 et 0,308 en fractions, nous pouvons déterminer laquelle est la plus grande.

      0,31 0,308
    Convertir en fractions. \(\frac{31}{100}\) \(\frac{308}{1000}\)
    Nous avons besoin d'un dénominateur commun pour les comparer. . .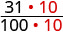
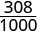      \(\frac{310}{1000}\) \(\frac{308}{1000}\)
    Tableau\(\PageIndex{2}\)

    Parce\(310 > 308\) que nous le savons\(\frac{310}{1000} > \frac{308}{1000}\). Par conséquent,\(0.31 > 0.308\).

    Remarquez ce que nous avons fait lors\(0.31\) de la conversion en fraction : nous avons commencé par la fraction\(\frac{31}{100}\) et nous avons terminé avec la fraction équivalente. La\(\frac{310}{1000}\)\(\frac{310}{1000}\) reconversion en décimale donne 0,310. Donc, 0,31 équivaut à 0,310. Écrire des zéros à la fin d'une décimale ne change pas sa valeur !

    \[\frac { 31 } { 100 } = \frac { 310 } { 1000 } \quad \text { and } \quad 0.31 = 0.310\]

    Nous disons que 0,31 et 0,310 sont des décimales équivalentes.

    DÉCIMALES ÉQUIVALENTES

    Deux décimales sont équivalentes si elles sont converties en fractions équivalentes.

    Nous utilisons des décimales équivalentes lorsque nous commandons des décimales.

    Les étapes que nous prenons pour classer les décimales sont résumées ici.

    COMMANDEZ DES DÉCIMALES.
    1. Écrivez les nombres les uns sous les autres, en alignant les décimales.
    2. Vérifiez si les deux numéros comportent le même nombre de chiffres. Si ce n'est pas le cas, écrivez des zéros à la fin de celui contenant le moins de chiffres pour les faire correspondre.
    3. Comparez les nombres comme s'ils étaient des nombres entiers.
    4. Classez les nombres en utilisant le signe d'inégalité approprié.
    Exercice\(\PageIndex{34}\)

    Commandez\(0.64 \text{ ___ } 0.6\) en utilisant\(<\) ou\(>\).

    Réponse

    \(\begin{array} { ll } { \text {Write the numbers one under the other, } } &{0.64} \\ { \text {lining up the decimal points. } } &{0.6} \\ \\ { \text {Add a zero to 0.6 to make it a decimal } } &{0.64} \\ {\text{with 2 decimal places.}} &{0.60} \\ {\text{Now they are both hundredths.}} &{} \\ \\ {\text{64 is greater than 60.}} &{64 > 60} \\ \\ {\text{64 hundredths is greater than 60 hundredths.}} &{0.64 > 0.60} \\ \\ {} &{0.64 > 0.6}\end{array}\)

    Exercice\(\PageIndex{35}\)

    Classez chacune des paires de nombres suivantes, en utilisant\(<\) ou\(>\) :\(0.42 \text{ ___ } 0.4\).

    Réponse

    \(>\)

    Exercice\(\PageIndex{36}\)

    Classez chacune des paires de nombres suivantes, en utilisant\(<\) ou\(>\) :\(0.18 \text{ ___ } 0.1\).

    Réponse

    \(>\)

    Exercice\(\PageIndex{37}\)

    Commandez\(0.83 \text{ ___ } 0.803\) en utilisant\(<\) ou\(>\).

    Réponse

    \(\begin{array} { ll } {} &{0.83\text{ ___ }0.803} \\ \\{ \text {Write the numbers one under the other, } } &{0.83} \\ { \text {lining up the decimal points. } } &{0.803} \\ \\ { \text {They do not have the same number of} } &{0.830} \\ {\text{digits.}} &{0.803} \\ {\text{Write one zero at the end of 0.83.}} &{} \\ \\ {\text{Since 830 > 803, 830 hundredths is}} &{0.830 > 0.803} \\ {\text{greater than 803 thousandths.}} &{}\\ \\ {} &{0.83 > 0.803}\end{array}\)

    Exercice\(\PageIndex{38}\)

    Classez chacune des paires de nombres suivantes, en utilisant\(<\) ou\(>\) :\(0.76 \text{ ___ } 0.706\).

    Réponse

    \(>\)

    Exercice\(\PageIndex{39}\)

    Classez chacune des paires de nombres suivantes, en utilisant\(<\) ou\(>\) :\(0.305 \text{ ___ } 0.35\).

    Réponse

    \(<\)

    Lorsque nous ordonnons des nombres décimaux négatifs, il est important de se rappeler comment ordonner les nombres entiers négatifs. N'oubliez pas que les plus grands nombres se trouvent à droite sur la ligne de numérotation. Par exemple, comme −2 se trouve à droite de -3 sur la ligne numérique, nous le savons\(−2>−3\). De même, les plus petits nombres se trouvent à gauche sur la ligne numérique. Par exemple, comme −9 se trouve à gauche de −6 sur la ligne numérique, nous le savons\(−9<−6\). Voir la figure\(\PageIndex{9}\).

    Une ligne numérique s'affiche qui va de moins 10 à 0. Aucun point n'est indiqué et les hashmarks existent à chaque entier compris entre moins 10 et 0.
    Figurine\(\PageIndex{9}\)

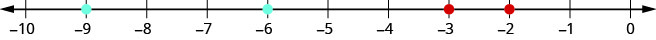
    Si nous zoomions sur l'intervalle entre 0 et -1, comme indiqué dans Exercice\(\PageIndex{40}\), nous verrions de la même manière que\(−0.2>−0.3\) et\(−0.9<−0.6\).

    Exercice\(\PageIndex{40}\)

    À utiliser\(<\) ou\(>\) à commander\(−0.1\text{ ___ }−0.8\).

    Réponse

    \(\begin{array} { ll } {} &{-0.1 \text{ ___ } -0.8} \\ \\ { \text { Write the numbers one under the other, lining up the } } &{-0.1} \\ { \text { decimal points. } } &{-0.8} \\ { \text { They have the same number of digits. } } &{} \\ \\ { \text { since } - 1 > - 8 , - 1 \text { tenth is greater than } - 8 \text { tenths. } } &{-0.1 > -0.8} \end{array}\)

    Exercice\(\PageIndex{41}\)

    Commandez la paire de chiffres suivante, en utilisant\(<\) ou\(>\) :\(−0.3\text{ ___ }−0.5\).

    Réponse

    \(>\)

    Exercice\(\PageIndex{42}\)

    Commandez la paire de chiffres suivante, en utilisant\(<\) ou\(>\) :\(−0.6\text{ ___ }−0.7\).

    Réponse

    \(>\)

    Concepts clés

    • La notation à racine carrée
      \(\sqrt{m}\) se lit comme suit : « la racine carrée de »\(m\). Si\(m = n^{2}\), alors\(\sqrt{m} = n\), pour\(n \geq 0\).
    • Décimales de commande
      1. Écrivez les nombres les uns sous les autres, en alignant les décimales.
      2. Vérifiez si les deux numéros comportent le même nombre de chiffres. Si ce n'est pas le cas, écrivez des zéros à la fin de celui contenant le moins de chiffres pour les faire correspondre.
      3. Comparez les nombres comme s'ils étaient des nombres entiers.
      4. Classez les nombres en utilisant le signe d'inégalité approprié.

    La pratique rend la perfection

    Simplifiez les expressions avec des racines

    Dans les exercices suivants, simplifiez.