1.6 : Visualiser les fractions
- Page ID
- 195301
À la fin de cette section, vous serez en mesure de :
- Trouvez des fractions équivalentes
- Simplifier les
- Multiplier les fractions
- Diviser les fractions
- Simplifier les expressions écrites avec une barre de fraction
- Traduisez des phrases en expressions avec des fractions
Vous trouverez une introduction plus complète aux sujets abordés dans cette section dans le chapitre sur la préalgèbre, Fractions.
Trouver des fractions équivalentes
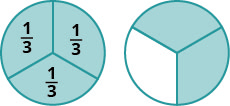
Les fractions sont un moyen de représenter des parties d'un tout. La fraction\(\dfrac{1}{3}\) signifie qu'un tout a été divisé en 3 parties égales et que chaque partie est l'une des trois parties égales. Voir la figure\(\PageIndex{1}\). La fraction\(\dfrac{2}{3}\) représente deux des trois parties égales. Dans la fraction\(\dfrac{2}{3}\), le 2 est appelé numérateur et le 3 est appelé dénominateur.
Une fraction est écrite\(\dfrac{a}{b}\), où\(b\neq 0\) et
- \(a\)est le numérateur et\(b\) le dénominateur.
Une fraction représente des parties d'un tout. Le dénominateur\(b\) est le nombre de parties égales en lesquelles l'ensemble a été divisé, et le numérateur\(a\) indique le nombre de parties incluses.
Si une tarte entière a été coupée en 6 morceaux et que nous mangeons les 6 morceaux, nous en avons mangé des\(\dfrac{6}{6}\) morceaux ou, en d'autres termes, une tarte entière.
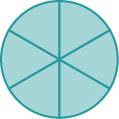
Donc\(\dfrac{6}{6}=1\). Cela nous amène à la propriété de l'un qui nous indique que n'importe quel nombre, sauf zéro, divisé par lui-même l'est\(1\).
\[\dfrac{a}{a} = 1 \quad (a \neq 0)\]
Tout nombre, sauf zéro, divisé par lui-même est un.
L'activité de mathématiques manipulatrices « Fractions équivalentes à une » vous aidera à mieux comprendre les fractions équivalentes à une.
Si une tarte était coupée en 6 morceaux et que nous mangions tous les 6, nous mangions des\(\dfrac{6}{6}\) morceaux ou, en d'autres termes, une tarte entière. Si la tarte était coupée en 8 morceaux et que nous mangions tous les 8, nous mangions des\(\dfrac{8}{8}\) morceaux ou une tarte entière. Nous avons mangé la même quantité, une tarte entière.
Les fractions\(\dfrac{6}{6}\) et\(\dfrac{8}{8}\) ont la même valeur, 1, et sont donc appelées fractions équivalentes. Les fractions équivalentes sont des fractions qui ont la même valeur.
Pensons aux pizzas cette fois. La figure\(\PageIndex{3}\) montre deux images : une pizza sur la gauche, coupée en deux morceaux égaux, et une deuxième pizza de même taille, coupée en huit morceaux sur la droite. C'est une façon de montrer qui\(\dfrac{1}{2}\) est équivalente à\(\dfrac{4}{8}\). En d'autres termes, ce sont des fractions équivalentes.
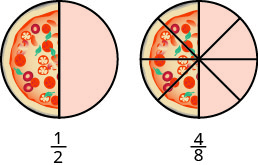
Les fractions équivalentes sont des fractions qui ont la même valeur.
Comment pouvons-nous utiliser les mathématiques pour\(\dfrac{1}{2}\) évoluer\(\dfrac{4}{8}\) ? Comment pourrait-on prendre une pizza coupée en 2 morceaux et la couper en 8 morceaux ? Nous pourrions couper chacune des 2 plus grandes pièces en 4 pièces plus petites ! La pizza entière serait ensuite coupée en 88 morceaux au lieu de 2. Mathématiquement, ce que nous avons décrit pourrait être écrit comme suit\(\dfrac{1\cdot 4}{2\cdot 4} = \dfrac{4}{8}\). Voir la figure\(\PageIndex{4}\).
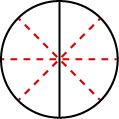
Ce modèle conduit à la propriété suivante :
Si\(a,b,c\) les chiffres sont où\(b\neq 0, c\neq 0\), alors
\[\dfrac{a}{b} = \dfrac{a\cdot c}{b\cdot c}\]
Si nous avions coupé la pizza différemment, nous aurions pu obtenir
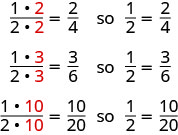
Donc, nous disons\(\dfrac{1}{2}\),\(\dfrac{2}{4}\)\(\dfrac{3}{6}\), et\(\dfrac{10}{20}\) sont des fractions équivalentes.
L'activité de mathématiques manipulatrices « Fractions équivalentes » vous aidera à mieux comprendre ce que signifie l'équivalence de deux fractions.
Trouvez trois fractions équivalentes à\(\dfrac{2}{5}\).
- Réponse
-
Pour trouver une fraction équivalente à\(\dfrac{2}{5}\), on multiplie le numérateur et le dénominateur par le même nombre. Nous pouvons choisir n'importe quel nombre, sauf zéro. Multiplions-les par 2, 3, puis 5.
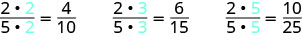
-
Donc,\(\dfrac{4}{10}\)\(\dfrac{6}{15}\), et\(\dfrac{10}{25}\) sont équivalents à\(\dfrac{2}{5}\).
Trouvez trois fractions équivalentes à\(\dfrac{3}{5}\).
- Réponse
-
\(\dfrac{6}{10}\),\(\dfrac{9}{15}\),\(\dfrac{12}{20}\) ; les réponses peuvent varier
Trouvez trois fractions équivalentes à\(\dfrac{4}{5}\).
- Réponse
-
\(\dfrac{8}{10}\),\(\dfrac{12}{15}\),\(\dfrac{16}{20}\) ; les réponses peuvent varier
Simplifier les
Une fraction est considérée comme simplifiée s'il n'existe aucun facteur commun, autre que 1, dans son numérateur et son dénominateur.
Par exemple,
- \(\dfrac{2}{3}\)est simplifié car il n'y a pas de facteurs communs de 2 et 3.
- \(\dfrac{10}{15}\)n'est pas simplifié car 5 est un facteur commun de 10 et 15.
Une fraction est considérée comme simplifiée si son numérateur et son dénominateur ne présentent aucun facteur commun.
L'expression réduire une fraction signifie simplifier la fraction. Nous simplifions ou réduisons une fraction en supprimant les facteurs communs que sont le numérateur et le dénominateur. Une fraction n'est pas simplifiée tant que tous les facteurs communs n'ont pas été supprimés. Si une expression contient des fractions, elle n'est pas complètement simplifiée tant que les fractions ne sont pas simplifiées.
Dans l'exercice\(\PageIndex{4}\), nous avons utilisé la propriété des fractions équivalentes pour trouver des fractions équivalentes. Nous allons maintenant utiliser la propriété des fractions équivalentes en sens inverse pour simplifier les fractions. Nous pouvons réécrire la propriété pour afficher les deux formes ensemble.
Si\(a,b,c\) sont des nombres où\(b\neq 0,c\neq 0\),
\[\text{then } \dfrac{a}{b} = \dfrac{a\cdot c}{b\cdot c} \text{ and } \dfrac{a\cdot c}{b\cdot c} = \dfrac{a}{b}\]
Simplifiez :\(-\dfrac{32}{56}\)
- Réponse
-
\(-\dfrac{32}{56}\) Réécrivez le numérateur et le dénominateur en indiquant les facteurs communs. \(-\dfrac{4\cdot 8}{7\cdot 8}\) Simplifiez en utilisant la propriété des fractions équivalentes \(-\dfrac{4}{7}\) Notez que la fraction\(-\dfrac{4}{7}\) est simplifiée car il n'y a plus de facteurs communs.
Simplifiez :\(-\dfrac{42}{54}\)
- Réponse
-
\(-\dfrac{7}{9}\)
Simplifiez :\(-\dfrac{42}{54}\)
- Réponse
-
\(-\dfrac{5}{9}\)
Parfois, il n'est pas facile de trouver les facteurs communs du numérateur et du dénominateur. Lorsque cela se produit, une bonne idée est de factoriser le numérateur et le dénominateur en nombre premier s. Ensuite, divisez les facteurs communs en utilisant la propriété des fractions équivalentes.
Simplifiez :\(-\dfrac{210}{385}\)
- Réponse
-



Simplifiez :\(-\dfrac{69}{120}\)
- Réponse
-
\(-\dfrac{23}{40}\)
Simplifiez :\(-\dfrac{120}{192}\)
- Réponse
-
\(-\dfrac{5}{8}\)
Nous résumons maintenant les étapes à suivre pour simplifier les fractions.
- Réécrivez le numérateur et le dénominateur pour montrer les facteurs communs.
Au besoin, factorisez d'abord le numérateur et le dénominateur en nombres premiers. - Simplifiez l'utilisation de la propriété des fractions équivalentes en divisant les facteurs communs.
- Multipliez les facteurs restants, si nécessaire.
Simplifiez :\(\dfrac{5x}{5y}\)
- Réponse
-
\(\dfrac{5x}{5y}\) Réécrivez en indiquant les facteurs communs, puis divisez les facteurs communs. 
Simplifiez. \(\dfrac{x}{y}\)
Simplifiez :\(\dfrac{7x}{7y}\)
- Réponse
-
\(\dfrac{x}{y}\)
Simplifiez :\(\dfrac{3a}{3b}\)
- Réponse
-
\(\dfrac{a}{b}\)
Multiplier les fractions
De nombreuses personnes trouvent qu'il est plus facile de multiplier et de diviser des fractions que d'ajouter et de soustraire des fractions. Nous allons donc commencer par la multiplication des fractions.
L'activité de mathématiques manipulatrices « Multiplication de fractions modèles » vous aidera à mieux comprendre la multiplication des fractions.Nous utiliserons un modèle pour vous montrer comment multiplier deux fractions et pour vous aider à vous souvenir de la procédure. Commençons par\(\dfrac{3}{4}\).

Maintenant, nous allons\(\dfrac{1}{2}\) décoller\(\dfrac{3}{4}\).

Notez que maintenant, l'ensemble est divisé en 8 parties égales. Donc\(\dfrac{1}{2}\cdot \dfrac{3}{4}=\dfrac{3}{8}\).
Pour multiplier les fractions, on multiplie les numérateurs et on multiplie les dénominateurs.
Si\(a,b,c\) et\(d\) sont des nombres où\(b\neq 0\) et\(d\neq 0\), alors
\[\dfrac{a}{b}\cdot\dfrac{c}{d} = \dfrac{ac}{bd}\]
Pour multiplier les fractions, multipliez les numérateurs et multipliez les dénominateurs.
Lors de la multiplication de fractions, les propriétés des nombres positifs et négatifs s'appliquent toujours, bien entendu. Il est conseillé de déterminer le signe du produit dans un premier temps. Dans l'exercice\(\PageIndex{13}\), nous allons multiplier le négatif et le positif, de sorte que le produit sera négatif.
Multipliez :\(-\dfrac{11}{12}\cdot \dfrac{5}{7}\)
- Réponse
-
La première étape consiste à trouver le signe du produit. Comme les signes sont différents, le produit est négatif.
\[\begin{array} {ll} {} & {-\dfrac{11}{12}\cdot \dfrac{5}{7}} \\{\text{Determine the sign of the product; multiply.}} &{-\dfrac{11\cdot 5}{12\cdot 7}} \\ {\text{Are there any common factors in the numerator}} &{} \\ {\text{and the denominator? No}} &{-\dfrac{55}{84}} \end{array}\]
Multipliez :\(-\dfrac{10}{28}\cdot \dfrac{8}{15}\)
- Réponse
-
\(-\dfrac{4}{21}\)
Multipliez :\(-\dfrac{9}{20}\cdot \dfrac{5}{12}\)
- Réponse
-
\(-\dfrac{3}{16}\)
Lorsque vous multipliez une fraction par un entier, il peut être utile d'écrire l'entier sous forme de fraction. Tout entier, a, peut être écrit sous la forme\(\dfrac{a}{1}\). Ainsi, par exemple,\(3 = \dfrac{3}{1}\).
Multipliez :\(-\dfrac{12}{5}(-20x)\)
- Réponse
-
Déterminez le signe du produit. Les signes sont les mêmes, donc le produit est positif.
\(-\dfrac{12}{5}(-20x)\) Écrivez\(20x\) sous forme de fraction. \(\dfrac{12}{5}(\dfrac{20x}{1})\) Multipliez. Réécrivez\(20\) pour montrer le facteur commun\(5\) et divisez-le. 
Simplifiez. \(48x\)
Multipliez :\(\dfrac{11}{3}(-9a)\)
- Réponse
-
\(-33a\)
Multipliez :\(\dfrac{13}{7}(-14b)\)
- Réponse
-
\(-26b\)
Diviser les fractions
Maintenant que nous savons comment multiplier les fractions, nous sommes presque prêts à diviser. Avant de pouvoir le faire, nous avons besoin d'un peu de vocabulaire.
L'inverse d'une fraction est trouvé en inversant la fraction, en plaçant le numérateur dans le dénominateur et le dénominateur dans le numérateur. La réciproque de l'\(\dfrac{2}{3}\)est\(\dfrac{3}{2}\).
Remarquez que\(\dfrac{2}{3}\cdot\dfrac{3}{2} = 1\). Un nombre et son inverse se multiplient par\(1\).
Pour obtenir un produit positif\(1\) lors de la multiplication de deux nombres, les nombres doivent avoir le même signe. Les réciproques doivent donc avoir le même signe.
La réciproque de\(-\dfrac{10}{7}\) est\(-\dfrac{7}{10}\), puisque\(-\dfrac{10}{7}(-\dfrac{7}{10}) = 1\).
La réciproque de l'\(\dfrac{a}{b}\)est\(\dfrac{b}{a}\).
Un nombre et son inverse se multiplient par un\(\dfrac{a}{b}\cdot\dfrac{b}{a} = 1\)
L'activité de mathématiques manipulatrices « Division des fractions modèles » vous aidera à mieux comprendre la division des fractions.
Pour diviser des fractions, on multiplie la première fraction par l'inverse de la seconde.
Si\(a,b,c\) et\(d\) sont des nombres où\(b\neq 0, c\neq 0\) et\(d\neq 0\), alors
\[\dfrac{a}{b}\div\dfrac{c}{d} = \dfrac{a}{b}\cdot\dfrac{d}{c}\]
Pour diviser des fractions, on multiplie la première fraction par l'inverse de la seconde.
Nous devons le dire\(b\neq 0, c\neq 0\) et\(d\neq 0\) être sûrs de ne pas diviser par zéro !
Diviser :\(-\dfrac{2}{3}\div\dfrac{n}{5}\)
- Réponse
-
\[\begin{array} {ll} {} & {-\dfrac{2}{3}\div \dfrac{n}{5}} \\{\text{To divide, multiply the first fraction by the}} &{-\dfrac{2}{3}\cdot\dfrac{5}{n}} \\ {\text{reciprocal of the second.}} &{} \\ {\text{Multiply.}} &{-\dfrac{10}{3n}} \end{array}\]
Diviser :\(-\dfrac{3}{5}\div\dfrac{p}{7}\).
- Réponse
-
\(-\dfrac{21}{5p}\)
Diviser :\(-\dfrac{5}{8}\div\dfrac{q}{3}\).
- Réponse
-
\(-\dfrac{15}{8q}\)
Trouvez le quotient :
\(-\dfrac{7}{18}\div (-\dfrac{14}{27})\)
- Réponse
-
\(-\dfrac{7}{18}\div(-\dfrac{14}{27})\) Pour diviser, multipliez la première fraction par l'inverse de la seconde. \(-\dfrac{7}{18}\cdot -\dfrac{27}{14}\) Déterminez le signe du produit, puis multipliez. \(\dfrac{7\cdot 27}{18\cdot 14}\) Réécrivez en indiquant les facteurs communs. 
Supprimez les facteurs courants. \(\dfrac{3}{2\cdot 2}\) Simplifiez. \(\dfrac{3}{4}\)
Trouvez le quotient :
\(-\dfrac{7}{8}\div (-\dfrac{14}{27})\)
- Réponse
-
\(\dfrac{4}{15}\)
Trouvez le quotient :
\(-\dfrac{7}{8}\div (-\dfrac{14}{27})\)
- Réponse
-
\(\dfrac{2}{3}\)
Il existe plusieurs façons de se souvenir des étapes à suivre pour multiplier ou diviser des fractions. L'une des solutions consiste à vous répéter les appels. Si vous faites cela à chaque fois que vous faites un exercice, les étapes seront mémorisées.
- « Pour multiplier les fractions, multipliez les numérateurs et multipliez les dénominateurs. »
- « Pour diviser des fractions, multipliez la première fraction par l'inverse de la seconde. »
Une autre méthode consiste à garder deux exemples à l'esprit :
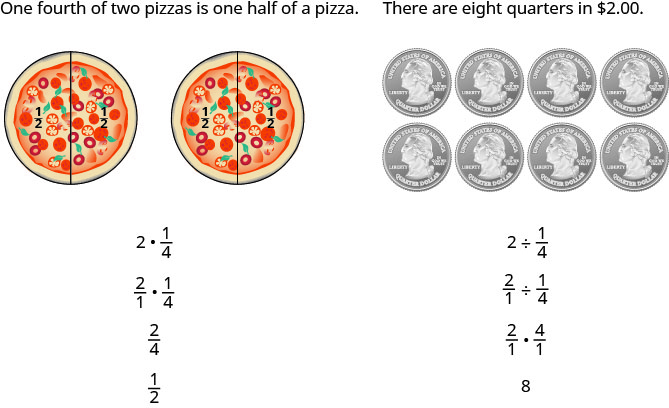
Les numérateurs ou dénominateurs de certaines fractions contiennent eux-mêmes des fractions. Une fraction dont le numérateur ou le dénominateur est une fraction est appelée fraction complexe.
Une fraction complexe est une fraction dont le numérateur ou le dénominateur contient une fraction.
Voici quelques exemples de fractions complexes :
\[\dfrac{\frac{6}{7}}{3} \quad \dfrac{\frac{3}{4}}{\frac{5}{8}} \quad \dfrac{\frac{x}{2}}{\frac{5}{6}}\]
Pour simplifier une fraction complexe, rappelons que la barre de fraction signifie division. Par exemple, la fraction complexe\(\dfrac{\frac{3}{4}}{\frac{5}{8}}\) signifie\(\dfrac{3}{4} \div \dfrac{5}{8}\).
Simplifiez :\(\dfrac{\frac{3}{4}}{\frac{5}{8}}\)
- Réponse
-
\(\dfrac{\frac{3}{4}}{\frac{5}{8}}\) Réécrivez en tant que division. \(\dfrac{3}{4} \div \dfrac{5}{8}\) Multipliez la première fraction par l'inverse de la seconde. \(\dfrac{3}{4} \cdot \dfrac{8}{5}\) Multipliez. \(\dfrac{3\cdot 8}{4\cdot 5}\) Recherchez les facteurs communs. 
Répartissez les facteurs communs et simplifiez. \(\dfrac{6}{5}\)
Simplifiez :\(\dfrac{\frac{2}{3}}{\frac{5}{6}}\)
- Réponse
-
\(\dfrac{4}{5}\)
Simplifiez :\(\dfrac{\frac{3}{7}}{\frac{6}{11}}\)
- Réponse
-
\(\dfrac{11}{14}\)
Simplifiez :\(\dfrac{\frac{x}{2}}{\frac{xy}{6}}\)
- Réponse
-
\(\dfrac{\frac{x}{2}}{\frac{xy}{6}}\) Réécrivez en tant que division. \(\dfrac{x}{2} \div \dfrac{xy}{6}\) Multipliez la première fraction par l'inverse de la seconde. \(\dfrac{x}{2} \cdot \dfrac{6}{xy}\) Multipliez. \(\dfrac{x\cdot 6}{2\cdot xy}\) Recherchez les facteurs communs. 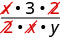
Répartissez les facteurs communs et simplifiez. \(\dfrac{3}{y}\)
Simplifiez :\(\dfrac{\frac{a}{8}}{\frac{ab}{6}}\)
- Réponse
-
\(\dfrac{3}{4b}\)
Simplifiez :\(\dfrac{\frac{p}{2}}{\frac{pq}{8}}\)
- Réponse
-
\(\dfrac{4}{q}\)
Simplifier les expressions avec une barre de fraction
La ligne qui sépare le numérateur du dénominateur d'une fraction est appelée barre de fraction. Une barre de fraction fait office de symbole de regroupement. L'ordre des opérations nous indique ensuite de simplifier le numérateur puis le dénominateur. Ensuite, nous nous divisons.
Pour simplifier l'expression\(\dfrac{5 - 3}{7 + 1}\), nous avons d'abord simplifié le numérateur et le dénominateur séparément. Ensuite, nous nous divisons.
\[\begin{array} {l} {\dfrac{5 - 3}{7 + 1}} \\ {\dfrac{2}{8}} \\ {\dfrac{1}{4}} \end{array}\]
- Simplifiez l'expression dans le numérateur. Simplifiez l'expression dans le dénominateur.
- Simplifiez la fraction.
Simplifiez :\(\dfrac{4 - 2(3)}{2^{2} + 2}\)
- Réponse
-
\[\begin{array} {ll} {} &{\dfrac{4 - 2(3)}{2^{2} + 2}} \\ {\text{Use the order of operations to simplify the}} &{\dfrac{4 - 6}{4 + 2}} \\ {\text{numerator and the denominator.}} &{} \\ {\text{Simplify the numerator and the denominator}} &{\dfrac{-2}{6}} \\ {\text{Simplify. A negative divided by a positive is negative.}} &{-\dfrac{1}{3}} \end{array}\]
Simplifiez :\(\dfrac{6 - 3(5)}{3^{2} + 3}\)
- Réponse
-
\(-\dfrac{3}{4}\)
Simplifiez :\(\dfrac{4 - 4(6)}{3^{2} + 3}\)
- Réponse
-
\(-\dfrac{5}{3}\)
Où va le signe négatif en une fraction ? Habituellement, le signe négatif se trouve devant la fraction, mais vous verrez parfois une fraction avec un numérateur négatif, ou parfois avec un dénominateur négatif. N'oubliez pas que les fractions représentent la division. Lorsque le numérateur et le dénominateur ont des signes différents, le quotient est négatif.
\[\begin{array} {ll} {\frac{-1}{3} = -\frac{1}{3}} &{\frac{\text{negative}}{\text{positive}} = \text{negative}} \\ {\frac{1}{-3} = -\frac{1}{3}} &{\frac{\text{positive}}{\text{negative}} = \text{negative}} \end{array}\]
Pour tout chiffre positif\(a\) et\(b\),
\[\dfrac{-a}{b} = \dfrac{a}{-b} = -\dfrac{a}{b}\]
Simplifiez :\(\frac{4(-3) + 6(-2)}{-3(2) - 2}\)
- Réponse
-
La barre de fraction agit comme un symbole de regroupement. Simplifiez donc complètement le numérateur et le dénominateur séparément.
\[\begin{array} {ll} {} &{\frac{4(-3) + 6(-2)}{-3(2) - 2}} \\{\text{Multiply.}} &{\frac{-12 + (-12)}{-6 - 2}} \\ {\text{Simplify.}} &{\frac{-24}{-8}} \\ {\text{Divide.}} &{3} \end{array}\]
Simplifiez :\(\frac{8(-2) + 4(-3)}{-5(2) + 3}\)
- Réponse
-
\(4\)
Simplifiez :\(\frac{7(-1) + 9(-3)}{-5(3) - 2}\)
- Réponse
-
\(2\)
Traduire des phrases en expressions avec des fractions
Maintenant que nous avons travaillé sur les fractions, nous sommes prêts à traduire des phrases qui aboutiraient à des expressions avec des fractions.
Les mots anglais quotient et ratio sont souvent utilisés pour décrire des fractions. Rappelez-vous que « quotient » signifie division. Le quotient de aa et bb est le résultat obtenu en divisant\(a\) par\(b\), ou\(\dfrac{a}{b}\).
Traduisez la phrase anglaise en une expression algébrique : le quotient de la différence entre\( m\) et\(n\) et\(p\).
- Réponse
-
Nous cherchons le quotient de la différence entre\(m\) et\(n\), et\(p\).. Cela signifie que nous voulons diviser la différence entre\(m\)\(n\) et et\(p\).
\[\dfrac{m - n}{p}\]
Traduisez la phrase anglaise en une expression algébrique : le quotient de la différence entre\(a\) et\(b\) et\(cd\).
- Réponse
-
\(\dfrac{a - b}{cd}\)
Traduisez la phrase anglaise en une expression algébrique : le quotient de la somme\(q\) de\(p\) et\(r\).
- Réponse
-
\(\dfrac{p + q}{r}\)
Concepts clés
- Propriété des fractions équivalentes : si ce\(a, b, c\) sont des nombres où\(b\neq 0, c\neq 0\), alors
\(\dfrac{a}{b} = \dfrac{a\cdot c}{b\cdot c}\) et\(\dfrac{a\cdot c}{b\cdot c} = \dfrac{a}{b}\) - Division des fractions : Si\(a, b, c\) et\(d\) sont des nombres où\(b\neq 0, c\neq 0\) et\(d \neq 0\), alors\(\dfrac{a}{b} \div \dfrac{c}{d} = \dfrac{a}{b} \cdot \dfrac{d}{c}\). Pour diviser des fractions, multipliez la première fraction par l'inverse de la seconde.
- Multiplication de fractions : Si\(a,b,c\) et\(d\) sont des nombres où\(b\neq 0, d\neq 0\), alors\(\dfrac{a}{b} \cdot \dfrac{c}{d} = \dfrac{ac}{bd}\). Pour multiplier les fractions, multipliez les numérateurs et multipliez les dénominateurs.
- Placement du signe négatif dans une fraction : pour tous les nombres positifs\(a\) et\(b\),\(\dfrac{-a}{a} = \dfrac{a}{-a} = -\dfrac{a}{b}\)
- Propriété de 1 :\(\dfrac{a}{a} = 1\) ; Tout nombre, sauf zéro, divisé par lui-même est un.
- Simplifier une fraction
- Réécrivez le numérateur et le dénominateur pour montrer les facteurs communs. Au besoin, factorisez d'abord le numérateur et le dénominateur en nombres premiers.
- Simplifiez l'utilisation de la propriété des fractions équivalentes en divisant les facteurs communs.
- Multipliez tous les facteurs restants.
- Simplifier une expression avec une barre de fraction
- Simplifiez l'expression dans le numérateur. Simplifiez l'expression dans le dénominateur.
- Simplifiez la fraction.
Lexique
- fraction complexe
- Une fraction complexe est une fraction dont le numérateur ou le dénominateur contient une fraction.
- dénominateur
- Le dénominateur est la valeur de la partie inférieure de la fraction qui indique le nombre de parties égales en lesquelles le tout a été divisé.
- fractions équivalentes
- Les fractions équivalentes sont des fractions qui ont la même valeur.
- fraction
- Une fraction est écrite\(\frac{a}{b}\)\(b\neq 0\), où a est le numérateur et b le dénominateur. Une fraction représente des parties d'un tout. Le dénominateur b est le nombre de parties égales en lesquelles l'ensemble a été divisé, et le numérateur aa indique le nombre de parties incluses.
- numérateur
- Le numérateur est la valeur située dans la partie supérieure de la fraction qui indique le nombre de parties de l'ensemble incluses.
- réciproque
- La réciproque de l'\(\frac{a}{b}\)est\(\frac{b}{a}\). Un nombre et son inverse se multiplient par un :\(\frac{a}{b}\cdot \frac{b}{a} = 1\).
- fraction simplifiée
- Une fraction est considérée comme simplifiée si son numérateur et son dénominateur ne présentent aucun facteur commun.


