1.6E : Exercices
- Page ID
- 195318
La pratique rend la perfection
Trouver des fractions équivalentes
Dans les exercices suivants, trouvez trois fractions équivalentes à la fraction donnée. Montrez votre travail en utilisant des chiffres ou de l'algèbre.
\(\dfrac{3}{8}\)
- Réponse
-
\(\dfrac{6}{16}\),\(\dfrac{9}{24}\),\(\dfrac{12}{32}\), les réponses peuvent varier
\(\dfrac{5}{8}\)
\(\dfrac{5}{9}\)
- Réponse
-
\(\dfrac{10}{18}\),\(\dfrac{15}{27}\),\(\dfrac{20}{36}\), les réponses peuvent varier
\(\dfrac{1}{8}\)
Simplifier les
Dans les exercices suivants, simplifiez.
\(-\dfrac{40}{88}\)
- Réponse
-
\(-\dfrac{5}{11}\)
\(-\dfrac{63}{99}\)
\(-\dfrac{108}{63}\)
- Réponse
-
\(-\dfrac{12}{7}\)
\(-\dfrac{104}{48}\)
\(\dfrac{120}{252}\)
- Réponse
-
\(\dfrac{10}{21}\)
\(\dfrac{182}{294}\)
\(-\dfrac{3x}{12y}\)
- Réponse
-
\(-\dfrac{x}{4y}\)
\(-\dfrac{4x}{32y}\)
\(\dfrac{14x^{2}}{21y}\)
- Réponse
-
\(\dfrac{2x^{2}}{3y}\)
\(\dfrac{24a}{32b^{2}}\)
Multiplier les fractions
Dans les exercices suivants, multipliez.
\(\dfrac{3}{4}\cdot \dfrac{9}{10}\)
- Réponse
-
\(\dfrac{27}{40}\)
\(\dfrac{4}{5}\cdot \dfrac{2}{7}\)
\(-\dfrac{2}{3}\cdot -\dfrac{3}{8}\)
- Réponse
-
\(\dfrac{1}{4}\)
\(-\dfrac{3}{4}\left(-\dfrac{4}{9}\right)\)
\(-\dfrac{5}{9}\cdot \dfrac{3}{10}\)
- Réponse
-
\(-\dfrac{1}{6}\)
\(-\dfrac{3}{8}\cdot \dfrac{4}{15}\)
\(\left(-\dfrac{14}{15}\right)\left(\dfrac{9}{20}\right)\)
- Réponse
-
\(-\dfrac{21}{50}\)
\(\left(-\dfrac{9}{10}\right)\left(\dfrac{25}{33}\right)\)
\(\left(-\dfrac{63}{84}\right)\left(-\dfrac{44}{90}\right)\)
- Réponse
-
\(\dfrac{11}{30}\)
\(\left(-\dfrac{63}{60}\right)\left(-\dfrac{40}{88}\right)\)
\(4\cdot \dfrac{5}{11}\)
- Réponse
-
\(\dfrac{20}{11}\)
\(5\cdot \dfrac{8}{3}\)
\(\dfrac{3}{7}\cdot 21n\)
- Réponse
-
9n
\(\dfrac{5}{6}\cdot 30m\)
\(-8\cdot\dfrac{17}{4}\)
- Réponse
-
−34
\((-1)\left(-\dfrac{6}{7}\right)\)
Diviser les fractions
Dans les exercices suivants, divisez.
\(\dfrac{3}{4}\div \dfrac{2}{3}\)
- Réponse
-
\(\dfrac{9}{8}\)
\(\dfrac{4}{5}\div \dfrac{3}{4}\)
\(-\dfrac{7}{9}\div \left(-\dfrac{7}{4}\right)\)
- Réponse
-
1
\(-\dfrac{5}{6}\div \left(-\dfrac{5}{6}\right)\)
\(\dfrac{3}{4}\div \dfrac{x}{11}\)
- Réponse
-
\(\dfrac{33}{4x}\)
\(\dfrac{2}{5}\div \dfrac{y}{9}\)
\(\dfrac{5}{18}\div -\dfrac{15}{24}\)
- Réponse
-
\(-\dfrac{4}{9}\)
\(\dfrac{7}{18}\div \left(-\dfrac{14}{27}\right)\)
\(\dfrac{8u}{15} \div \dfrac{12v}{25}\)
- Réponse
-
\(\dfrac{10u}{9v}\)
\(\dfrac{12r}{25}\div \dfrac{18s}{35}\)
\(-5\div \dfrac{1}{2}\)
- Réponse
-
-10
\(-3\div \dfrac{1}{4}\)
\(\dfrac{3}{4}\div (-12)\)
- Réponse
-
\(\dfrac{1}{16}\)
\(-15\div -\dfrac{5}{3}\)
Dans les exercices suivants, simplifiez.
\(\dfrac{-\dfrac{8}{21}}{\dfrac{12}{35}}\)
- Réponse
-
\(-\dfrac{10}{9}\)
\(\dfrac{-\dfrac{9}{16}}{\dfrac{33}{40}}\)
\(\dfrac{-\dfrac{4}{5}}{2}\)
- Réponse
-
\(-\dfrac{2}{5}\)
\(\dfrac{5}{\dfrac{3}{10}}\)
\(\dfrac{\dfrac{m}{3}}{\dfrac{n}{2}}\)
- Réponse
-
\(\dfrac{2m}{3n}\)
\(\dfrac{-\dfrac{3}{8}}{-\dfrac{y}{12}}\)
Simplifier les expressions écrites avec une barre de fraction
Dans les exercices suivants, simplifiez.
\(\dfrac{22 + 3}{10}\)
- Réponse
-
\(\dfrac{5}{2}\)
\(\dfrac{19 - 4}{6}\)
\(\dfrac{48}{24 - 15}\)
- Réponse
-
\(\dfrac{16}{3}\)
\(\dfrac{46}{4 + 4}\)
\(\dfrac{-6 + 6}{8 + 4}\)
- Réponse
-
0
\(\dfrac{-6 + 3}{17 - 8}\)
\(\dfrac{4\cdot 3}{6\cdot 6}\)
- Réponse
-
\(\dfrac{1}{3}\)
\(\dfrac{6\cdot 6}{9\cdot 2}\)
\(\dfrac{4^{2} - 1}{25}\)
- Réponse
-
\(\dfrac{3}{5}\)
\(\dfrac{7^{2} + 1}{60}\)
\(\dfrac{8\cdot 3 + 2\cdot 9}{14 + 3}\)
- Réponse
-
\(2\dfrac{8}{17}\)
\(\dfrac{9\cdot 6 - 4\cdot 7}{22 + 3}\)
\(\dfrac{5\cdot 6 - 3\cdot 4}{4\cdot 5 -2\cdot 3}\)
- Réponse
-
\(\dfrac{9}{7}\)
\(\dfrac{8\cdot 9 - 7\cdot 6}{5\cdot 6 - 9\cdot 2}\)
\(\dfrac{5^{2} - 3^{2}}{3 - 5}\)
- Réponse
-
\(-8\)
\(\dfrac{6^{2} - 4^{2}}{4 - 6}\)
\(\dfrac{7\cdot 4 - 2(8 - 5)}{9\cdot 3 - 3\cdot 5}\)
- Réponse
-
\(\dfrac{11}{6}\)
\(\dfrac{9\cdot 7 - 3(12- 8)}{8\cdot 7- 6\cdot 6}\)
\(\dfrac{9(8-2)-3(15-7)}{6(7-1) - 3(17-9)}\)
- Réponse
-
\(\dfrac{5}{2}\)
\(\dfrac{8(9-2) - 4(14 - 9)}{7(8-3)-3(16 -9)}\)
Traduisez des phrases en expressions avec des fractions
Dans les exercices suivants, traduisez chaque phrase anglaise en une expression algébrique.
le quotient\(r\) et la somme\(s\) de\(10\)
- Réponse
-
\(\dfrac{r}{s + 10}\)
le quotient\(A\) et la différence entre\(3\) et\(B\)
le quotient de la différence entre\(x\) et\(y\),\(−3\)
- Réponse
-
\(\dfrac{x - y}{-3}\)
le quotient de la somme de\(m\) et\(n\),\(4q\)
Mathématiques quotidiennes
Cuisson. Une recette de biscuits aux pépites de chocolat demande une\(\frac{3}{4}\) tasse de cassonade. Imelda veut doubler la recette.
- De quelle quantité de cassonade aura besoin Imelda ? Montrez votre calcul.
- Les tasses à mesurer sont généralement livrées par lots de\(\frac{1}{4}\)\(\frac{1}{3}\),\(\frac{1}{2}\), et\(1\) de tasses. Dessinez un diagramme pour montrer deux manières différentes dont Imelda peut mesurer la cassonade nécessaire pour doubler la recette de biscuits.
- Réponse
-
- \(1\frac{1}{2}\)tasses
- les réponses varieront
Cuisson. Nina prépare 4 casseroles de fudge à servir après un récital de musique. Pour chaque casserole, elle a besoin d'une\(\frac{2}{3}\) tasse de lait condensé.
- De quelle quantité de lait concentré Nina aura-t-elle besoin ? Montrez votre calcul.
- Les tasses à mesurer sont généralement livrées par lots de\(\frac{1}{4}\)\(\frac{1}{3}\),\(\frac{1}{2}\), et\(1\) de tasses. Dessinez un diagramme pour montrer deux manières différentes dont Nina peut mesurer le lait condensé nécessaire pour\(4\) les casseroles de fudge.
Portions Don a acheté un paquet de bonbons en vrac qui pèse des\(5\) kilos. Il veut vendre les bonbons dans de petits sacs qui contiennent de la\(\frac{1}{4}\) livre. Combien de petits sacs de bonbons peut-il remplir à partir du colis en vrac ?
- Réponse
-
\(20\)sacs
Kristen a des\(\frac{3}{4}\) mètres de ruban qu'elle veut couper à parts\(6\) égales pour fabriquer des rubans à cheveux pour les\(6\) poupées de sa fille. Combien de temps durera le ruban à cheveux de chaque poupée ?
Exercices d'écriture
Rafael voulait commander une demi-pizza de taille moyenne dans un restaurant. Le serveur lui a dit qu'une pizza de taille moyenne pouvait être coupée\(6\) ou\(8\) tranchée. Préférerait-il\(3\) en\(6\) tranches ou\(4\) en\(8\) tranches ? Rafael a répondu que, comme il n'avait pas très faim, il\(3\) préférait ne pas avoir de\(6\) tranches. Expliquez ce qui ne va pas dans le raisonnement de Rafael.
- Réponse
-
Les réponses peuvent varier
Donnez un exemple de la vie de tous les jours qui montre comment cela\(\dfrac{1}{2}\cdot \dfrac{2}{3}\) fonctionne\(\dfrac{1}{3}\).
Expliquez comment vous trouvez l'inverse d'une fraction.
- Réponse
-
Les réponses peuvent varier
Expliquez comment vous trouvez l'inverse d'un nombre négatif.
Auto-vérification
ⓐ Une fois les exercices terminés, utilisez cette liste de contrôle pour évaluer votre maîtrise des objectifs de cette section.
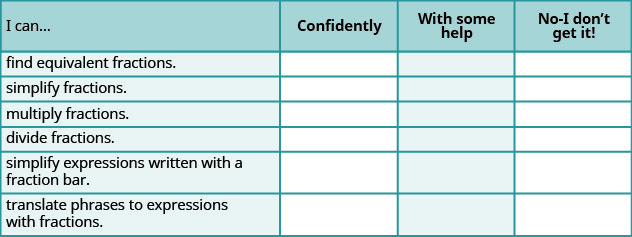
ⓑ Après avoir examiné la liste de contrôle, pensez-vous être bien préparé pour la section suivante ? Pourquoi ou pourquoi pas ?


