1.7 : Ajouter et soustraire des fractions
- Page ID
- 195361
À la fin de cette section, vous serez en mesure de :
- Additionner ou soustraire des fractions ayant un dénominateur commun
- Ajouter ou soustraire des fractions avec différents dénominateurs
- Utilisez l'ordre des opérations pour simplifier les fractions complexes
- Évaluez des expressions variables avec des fractions
Vous trouverez une introduction plus complète aux sujets abordés dans cette section dans le chapitre sur la préalgèbre, Fractions.
Ajouter ou soustraire des fractions avec un dénominateur commun
Lorsque nous avons multiplié des fractions, nous avons simplement multiplié les numérateurs et multiplié les dénominateurs directement. Pour ajouter ou soustraire des fractions, elles doivent avoir un dénominateur commun.
Si\(a,b\) et\(c\) sont des nombres où\(c\neq 0\), alors
\[\dfrac{a}{c} + \dfrac{b}{c} = \dfrac{a + b}{c} \quad \text{and} \quad \dfrac{a}{c} - \dfrac{b}{c} = \dfrac{a - b}{c}\]
Pour ajouter ou soustraire des fractions, ajoutez ou soustrayez les numérateurs et placez le résultat au-dessus du dénominateur commun.
Les activités de mathématiques manipulatrices « Addition de fractions modèles » et « Soustraction de fractions modèles » vous aideront à mieux comprendre l'addition et la soustraction de fractions.
Trouvez la somme :\(\dfrac{x}{3} + \dfrac{2}{3}\).
- Réponse
-
\[\begin{array} {ll} {} &{\dfrac{x}{3} + \dfrac{2}{3}} \\ {\text{Add the numerators and place the sum over the common denominator}} &{\dfrac{x + 2}{3}} \end{array}\]
Trouvez la somme :\(\dfrac{x}{4} + \dfrac{3}{4}\).
- Réponse
-
\(\dfrac{x + 3}{4}\)
Trouvez la somme :\(\dfrac{y}{8} + \dfrac{5}{8}\).
- Réponse
-
\(\dfrac{y + 5}{8}\)
Trouvez la différence :\(-\dfrac{23}{24} - \dfrac{13}{24}\)
- Réponse
-
\[\begin{array} {ll} {} &{-\dfrac{23}{24} - \dfrac{13}{24}} \\ {\text{Subtract the numerators and place the }} &{\dfrac{-23 - 13}{24}} \\ {\text{difference over the common denominator}} &{} \\ {\text{Simplify.}} &{\dfrac{-36}{24}} \\ {\text{Simplify. Remember, }-\dfrac{a}{b} = \dfrac{-a}{b}} &{-\dfrac{3}{2}} \end{array}\]
Trouvez la différence :\(-\dfrac{19}{28} - \dfrac{7}{28}\)
- Réponse
-
\(-\dfrac{26}{28}\)
Trouvez la différence :\(-\dfrac{27}{32} - \dfrac{1}{32}\)
- Réponse
-
\(-\dfrac{7}{8}\)
Trouvez la différence :\(-\dfrac{10}{x} - \dfrac{4}{x}\)
- Réponse
-
\[\begin{array} {ll} {} &{-\dfrac{10}{x} - \dfrac{4}{x}} \\ {\text{Subtract the numerators and place the }} &{\dfrac{-14}{x}} \\ {\text{difference over the common denominator}} &{} \\ {\text{Rewrite with the sign in front of the fraction.}} &{-\dfrac{14}{x}} \end{array}\]
Trouvez la différence :\(-\dfrac{9}{x} - \dfrac{7}{x}\)
- Réponse
-
\(-\dfrac{16}{x}\)
Trouvez la différence :\(-\dfrac{17}{a} - \dfrac{5}{a}\)
- Réponse
-
\(-\dfrac{22}{a}\)
Simplifiez :\(\dfrac{3}{8} + (-\dfrac{5}{8}) - \dfrac{1}{8}\)
- Réponse
-
\[\begin{array} {ll} {\text{Add and Subtract fractions — do they have a }} &{\frac{3}{8} + (-\frac{5}{8}) - \frac{1}{8}} \\ {\text{common denominator? Yes.}} &{} \\ {\text{Add and subtract the numerators and place }} &{\frac{3 + (-5) - 1}{8}} \\ {\text{the result over the common denominator.}} &{} \\ {\text{Simplify left to right.}} &{\frac{-2 - 1}{8}} \\ {\text{Simplify.}} &{-\frac{3}{8}} \end{array}\]
Simplifiez :\(\dfrac{2}{9} + (-\dfrac{4}{9}) - \dfrac{7}{9}\)
- Réponse
-
\(-1\)
Simplifiez :\(\dfrac{2}{5} + (-\dfrac{4}{9}) - \dfrac{7}{9}\)
- Réponse
-
\(-\dfrac{2}{3}\)
Ajouter ou soustraire des fractions avec différents dénominateurs
Comme nous l'avons vu, pour additionner ou soustraire des fractions, leurs dénominateurs doivent être les mêmes. Le plus petit dénominateur commun (LCD) de deux fractions est le plus petit nombre pouvant être utilisé comme dénominateur commun des fractions. L'écran LCD des deux fractions est le plus petit multiple commun (LCM) de leurs dénominateurs.
Le plus petit dénominateur commun (LCD) de deux fractions est le plus petit multiple commun (LCM) de leurs dénominateurs.
L'activité de mathématiques manipulatrices « Trouver le plus petit dénominateur commun » vous aidera à mieux comprendre l'écran LCD.
Après avoir trouvé le plus petit dénominateur commun de deux fractions, nous convertissons les fractions en fractions équivalentes à l'aide de l'écran LCD. La combinaison de ces étapes nous permet d'additionner et de soustraire des fractions car leurs dénominateurs seront les mêmes !
Ajoutez :\(\dfrac{7}{12} + \dfrac{5}{18}\)
- Réponse
-



Ajoutez :\(\dfrac{7}{12} + \dfrac{11}{15}\)
- Réponse
-
\(\dfrac{79}{60}\)
Ajoutez :\(\dfrac{7}{12} + \dfrac{11}{15}\)
- Réponse
-
\(\dfrac{103}{60}\)
- Ont-ils un dénominateur commun ?
- Oui, passez à l'étape 2.
- NON : réécrivez chaque fraction à l'aide de l'écran LCD (le plus petit dénominateur commun). Trouvez l'écran LCD. Changez chaque fraction en une fraction équivalente avec l'écran LCD comme dénominateur.
- Ajoutez ou soustrayez les fractions.
- Simplifiez, si possible.
Pour trouver les fractions équivalentes nécessaires pour créer les dénominateurs communs, il existe un moyen rapide de trouver le nombre dont nous avons besoin pour multiplier à la fois le numérateur et le dénominateur. Cette méthode fonctionne si nous avons trouvé l'écran LCD en tenant compte des nombres premiers.
Examinez les facteurs de l'écran LCD, puis de chaque colonne au-dessus de ces facteurs. Les facteurs « manquants » de chaque dénominateur sont les nombres dont nous avons besoin.

Dans Exercice\(\PageIndex{13}\), l'écran LCD, 36, possède deux facteurs de 2 et deux facteurs de 3.
Le numérateur 12 a deux facteurs de 2 mais un seul de 3, il en « manque » donc un, 3. On multiplie le numérateur et le dénominateur par 3.
Il manque un facteur de 2 au numérateur 18. Nous multiplions donc le numérateur et le dénominateur par 2.
Nous appliquerons cette méthode lorsque nous soustrairons les fractions dans l'exercice\(\PageIndex{16}\).
Soustraire :\(\dfrac{7}{15} - \dfrac{19}{24}\)
- Réponse
-
Les fractions ont-elles un dénominateur commun ? Non, nous devons donc trouver l'écran LCD.
Trouvez l'écran LCD. 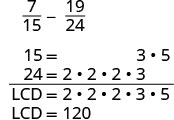
Remarquez que 15 « manque » trois facteurs de 2 et 24 « manque » le 5 parmi les facteurs de l'écran LCD. Nous multiplions donc 8 dans la première fraction et 5 dans la seconde fraction pour obtenir l'écran LCD. Réécrivez sous forme de fractions équivalentes avec l'écran LCD. 
Simplifiez. 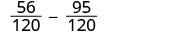
Soustraire. \(-\dfrac{39}{120}\) Vérifiez si la réponse peut être simplifiée. \(-\dfrac{13\cdot3}{40\cdot3}\) 39 et 120 ont tous deux un facteur 3. Simplifiez. \(-\dfrac{13}{40}\) Ne simplifiez pas les fractions équivalentes ! Si vous le faites, vous reviendrez aux fractions d'origine et perdrez le dénominateur commun !
Soustraire :\(\dfrac{13}{24} - \dfrac{17}{32}\)
- Réponse
-
\(\dfrac{1}{96}\)
Soustraire :\(\dfrac{7}{15} - \dfrac{19}{24}\)
- Réponse
-
\(\dfrac{75}{224}\)
Dans l'exemple suivant, l'une des fractions possède une variable dans son numérateur. Notez que nous effectuons les mêmes étapes que lorsque les deux numérateurs sont des nombres.
Ajoutez :\(\dfrac{3}{5} + \dfrac{x}{8}\)
- Réponse
-
Les fractions ont des dénominateurs différents.
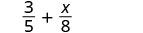
Trouvez l'écran LCD. 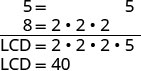
Réécrivez sous forme de fractions équivalentes avec l'écran LCD. 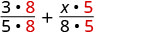
Simplifiez. 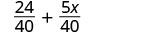
Ajoutez. 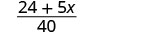
N'oubliez pas que nous ne pouvons ajouter que des termes similaires :\(24\) et ne\(5x\) sommes pas des termes similaires.
Ajoutez :\(\dfrac{y}{6} + \dfrac{7}{9}\)
- Réponse
-
\(\dfrac{3y + 14}{18}\)
Ajoutez :\(\dfrac{x}{6} + \dfrac{7}{15}\)
- Réponse
-
\(\dfrac{15x + 42}{153}\)
Nous avons maintenant les quatre opérations pour les fractions. Le tableau\(\PageIndex{1}\) résume les opérations de fraction.
| Multiplication de | Division des fractions |
| \(\dfrac{a}{b}\cdot \dfrac{c}{d} = \dfrac{ac}{bd}\) Multipliez les numérateurs et multipliez les dénominateurs |
\(\dfrac{a}{b}\div \dfrac{c}{d} = \dfrac{a}{b} \cdot \dfrac{d}{c}\) Multipliez la première fraction par l'inverse de la seconde. |
| Addition de fractions | Soustraction de fractions |
| \(\dfrac{a}{c} + \dfrac{b}{c} = \dfrac{a + b}{c}\) Additionnez les numérateurs et placez la somme au-dessus du dénominateur commun. |
\(\dfrac{a}{c} + \dfrac{b}{c} = \dfrac{a + b}{c}\) Soustrayez les numérateurs et placez la différence au-dessus du dénominateur commun. |
| Pour multiplier ou diviser des fractions, un écran LCD n'est pas nécessaire. Pour ajouter ou soustraire des fractions, un écran LCD est nécessaire. | |
Simplifiez :
- \(\dfrac{5x}{6} - \dfrac{3}{10}\)
- \(\dfrac{5x}{6}\cdot \dfrac{3}{10}\).
- Réponse
-
Demandez d'abord : « En quoi consiste l'opération ? » Une fois que nous aurons identifié l'opération, cela déterminera si nous avons besoin d'un dénominateur commun. N'oubliez pas que nous avons besoin d'un dénominateur commun pour additionner ou soustraire, mais pas pour multiplier ou diviser.
1. En quoi consiste l'opération ? L'opération est la soustraction.
\[\begin{array} {ll} {\text{Do the fractions have a common denominator? No.}} &{\frac{5x}{6} - \frac{3}{10}} \\ {\text{Rewrite each fractions as an equivalent fraction with the LCD.}} &{\frac{5x\cdot 5}{6\cdot 5} - \frac{3\cdot3}{10\cdot3}} \\ {} &{\frac{25x}{30} - \frac{9}{30}} \\{\text{Subtract the numerators and place the difference over the}} &{\frac{25x - 9}{30}} \\ {\text{common denominators.}} &{} \\ {\text{Simplify, if possible. There are no common factors.}} &{} \\ {\text{The fraction is simplified.}} &{} \end{array}\]
2. En quoi consiste l'opération ? Multiplication.
\[\begin{array} {ll} {} &{\frac{5x}{6}\cdot \frac{3}{10}} \\ {\text{To multiply fractions, multiply the numerators and multiply}} &{\frac{5x\cdot 3}{6\cdot 10}} \\ {\text{the denominators}} &{} \\{\text{Rewrite, showing common factors.}} &{\frac{\not 5 x\cdot\not3}{2\cdot\not3\cdot2\cdot\not5}} \\ {\text{common denominators.}} &{} \\ {\text{Simplify.}} &{\frac{x}{4}} \end{array}\]
Simplifiez :
- \(\dfrac{3a}{4} - \dfrac{8}{9}\)
- \(\dfrac{3a}{4}\cdot\dfrac{8}{9}\)
- Réponse
-
- \(\dfrac{27a - 32}{36}\)
- \(\dfrac{2a}{3}\)
Simplifiez :
- \(\dfrac{4k}{5} - \dfrac{1}{6}\)
- \(\dfrac{4k}{5}\cdot\dfrac{1}{6}\)
- Réponse
-
- \(\dfrac{24k - 5}{30}\)
- \(\dfrac{2k}{15}\)
Utiliser l'ordre des opérations pour simplifier les fractions complexes
Nous avons vu qu'une fraction complexe est une fraction dans laquelle le numérat ou le dénominateur contient une fraction. La barre de fraction indique la division. Nous avons simplifié la fraction complexe\(\dfrac{\frac{3}{4}}{\frac{5}{8}}\) en divisant\(\dfrac{3}{4}\) par\(\dfrac{5}{8}\).
Nous allons maintenant examiner les fractions complexes dont le numérateur ou le dénominateur contient une expression qui peut être simplifiée. Il faut donc d'abord simplifier complètement le numérateur et le dénominateur séparément en utilisant l'ordre des opérations. Ensuite, nous divisons le numérateur par le dénominateur.
Simplifiez :\(\dfrac{(\frac{1}{2})^{2}}{4 + 3^{2}}\)
- Réponse
-



Simplifiez :\(\dfrac{(\frac{1}{3})^{2}}{2^{3} + 2}\)
- Réponse
-
\(\dfrac{1}{90}\)
Simplifiez :\(\dfrac{1 + 4^{2}}{(\frac{1}{4})^{2}}\)
- Réponse
-
\(272\)
- Simplifiez le numérateur.
- Simplifiez le dénominateur.
- Divisez le numérateur par le dénominateur. Simplifiez si possible.
Simplifiez :\(\dfrac{\frac{1}{2} + \frac{2}{3}}{\frac{3}{4} - \frac{1}{6}}\)
- Réponse
-
\[\begin{array} {ll} {} &{\frac{(\frac{1}{2} + \frac{2}{3})}{(\frac{3}{4} - \frac{1}{6})}} \\ {\text{Simplify the numerator (LCD = 6) and simplify the denominator (LCD = 12).}} &{\frac{(\frac{3}{6} + \frac{4}{6})}{(\frac{9}{12} - \frac{2}{12})}} \\ {\text{Simplify.}} &{\frac{(\frac{7}{6})}{(\frac{7}{12})}} \\{\text{Divide the numerator by the denominator.}} &{\frac{7}{6}\div\frac{7}{12}} \\ {\text{Simplify.}} &{\frac{7}{6}\cdot\frac{12}{7}} \\ {\text{Divide out common factors.}} &{\frac{7\cdot6\cdot2}{6\cdot7}} \\ {\text{Simplify.}} &{2} \end{array}\]
Simplifiez :\(\dfrac{\frac{1}{3} + \frac{1}{2}}{\frac{3}{4} - \frac{1}{3}}\)
- Réponse
-
\(2\)
Simplifiez :\(\dfrac{\frac{2}{3} - \frac{1}{2}}{\frac{1}{4} + \frac{1}{3}}\)
- Réponse
-
\(\dfrac{2}{7}\)
Évaluer des expressions variables avec des fractions
Nous avons déjà évalué des expressions, mais nous pouvons maintenant évaluer des expressions avec des fractions. N'oubliez pas que pour évaluer une expression, nous substituons la valeur de la variable dans l'expression, puis nous simplifions.
Évaluez\(x + \dfrac{1}{3}\) quand
- \(x = -\dfrac{1}{3}\)
- \(x = -\dfrac{3}{4}\)
- Réponse
-
1. Pour évaluer\(x + \dfrac{1}{3}\) quand\(x = -\dfrac{1}{3}\), remplacez\(-\dfrac{1}{3}\)\(x\) dans l'expression.
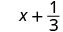
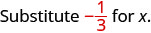
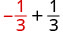
Simplifiez. \(0\)
2. Pour évaluer\(x + \dfrac{1}{3}\) quand\(x = -\dfrac{3}{4}\), remplacez\(-\dfrac{3}{4}\)\(x\) dans l'expression.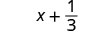

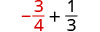
Réécrivez sous forme de fractions équivalentes avec l'écran LCD, 12. 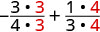
Simplifiez. 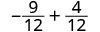
Ajoutez. \(-\dfrac{5}{12}\)
Évaluez\(x + \dfrac{3}{4}\) quand
- \(x = -\dfrac{7}{4}\)
- \(x = -\dfrac{5}{4}\)
- Réponse
-
- \(-1\)
- \(-\dfrac{1}{2}\)
Évaluez\(y + \dfrac{1}{2}\) quand
- \(y = \dfrac{2}{3}\)
- \(y = -\dfrac{3}{4}\)
- Réponse
-
- \(\dfrac{7}{6}\)
- \(-\dfrac{1}{12}\)
Évaluez\(-\dfrac{5}{6} - y\) quand\(y = -\dfrac{2}{3}\)
- Réponse
-
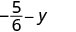
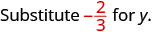
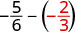
Réécrivez sous forme de fractions équivalentes avec l'écran LCD,\(6\). 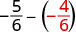
Soustraire. 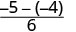
Simplifiez. \(-\dfrac{1}{6}\)
Évaluez\(y + \dfrac{1}{2}\) quand\(y = \dfrac{2}{3}\)
- Réponse
-
\(-\dfrac{1}{4}\)
Évaluez\(y + \dfrac{1}{2}\) quand\(y = \dfrac{2}{3}\)
- Réponse
-
\(-\dfrac{17}{8}\)
Évaluez\(2x^{2}y\) quand\(x = \dfrac{1}{4}\) et\(y = -\dfrac{2}{3}\).
- Réponse
-
Substituez les valeurs dans l'expression.
\(2x^{2}y\) 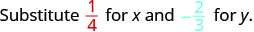
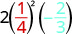
Simplifiez d'abord les exposants \(2(\frac{1}{16})(-\frac{2}{3})\) Multipliez. Répartissez les facteurs communs. Notez\(16\) que nous écrivons\(2\cdot2\cdot4\) pour le rendre facile à retirer \(-\frac{\not2\cdot1\cdot\not2}{\not2\cdot\not2\cdot4\cdot3}\) Simplifiez. \(-\frac{1}{12}\)
Évaluez\(3ab^{2}\) quand\(a = -\dfrac{2}{3}\) et\(b = -\dfrac{1}{2}\).
- Réponse
-
\(-\dfrac{1}{2}\)
Évaluez\(4c^{3}d\) quand\(c = -\dfrac{1}{2}\) et\(d = -\dfrac{4}{3}\).
- Réponse
-
\(\dfrac{2}{3}\)
L'exemple suivant ne comportera que des variables, pas de constantes.
Évaluez\(\dfrac{p + q}{r}\) quand\(p = -4, q = -2\), et\(r = 8\).
- Réponse
-
Pour évaluer\(\dfrac{p + q}{r}\) quand et\(p = -4, q = -2\)\(r = 8\), nous substituons les valeurs dans l'expression.
\(\dfrac{p + q}{r}\) 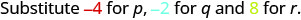
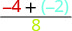
Ajoutez d'abord le numérateur. \(\dfrac{-6}{8}\) Simplifiez. \(-\dfrac{3}{4}\)
Évaluez\(\dfrac{a+b}{c}\) quand\(a = -8, b = -7\), et\(c = 6\).
- Réponse
-
\(-\dfrac{5}{2}\)
Évaluez\(\dfrac{x+y}{z}\) quand\(x = 9, y = -18\), et\(z = -6\).
- Réponse
-
\(\dfrac{3}{2}\)
Concepts clés
- Addition et soustraction de fractions : Si\(a, b\) et\(c\) sont des nombres où\(c\neq 0\), alors
\(\dfrac{a}{c} + \dfrac{b}{c} = \dfrac{a+b}{c}\) et\(\dfrac{a}{c} - \dfrac{b}{c} = \dfrac{a-b}{c}\)
Pour ajouter ou soustraire des fractions, ajoutez ou soustrayez les numérateurs et placez le résultat au-dessus du dénominateur commun.
- Stratégie pour ajouter ou soustraire des fractions
- Ont-ils un dénominateur commun ?
Oui, passez à l'étape 2.
Non : réécrivez chaque fraction à l'aide de l'écran LCD (Least Common Denominator). Trouvez l'écran LCD. Changez chaque fraction en une fraction équivalente avec l'écran LCD comme dénominateur. - Ajoutez ou soustrayez les fractions.
- Simplifiez, si possible. Pour multiplier ou diviser des fractions, aucun écran LCD n'est nécessaire. Pour ajouter ou soustraire des fractions, un écran LCD est nécessaire.
- Ont-ils un dénominateur commun ?
- Simplifier les fractions
- Simplifiez le numérateur.
- Simplifiez le dénominateur.
- Divisez le numérateur par le dénominateur. Simplifiez si possible.


