5.3 : Propriétés des exposants et notation scientifique
- Page ID
- 194191
À la fin de cette section, vous serez en mesure de :
- Simplifier les expressions à l'aide des propriétés des exposants
- Utiliser la définition d'un exposant négatif
- Utiliser la notation scientifique
Avant de commencer, répondez à ce questionnaire de préparation.
Simplifier les expressions à l'aide des propriétés des exposants
N'oubliez pas qu'un exposant indique une multiplication répétée de la même quantité. Par exemple, dans l'expression\(a^m\), l'exposant nous\(m\) indique combien de fois nous utilisons la base\(a\) comme facteur.
\[a^{m}= \underbrace{a \cdot a \cdot a \cdot \ldots \cdot a}_{\color{cyan}{\text{m factors}}} \nonumber\]
Par exemple
\[(-9)^{5}= \underbrace{ (-9)\cdot (-9)\cdot (-9)\cdot (-9) \cdot (-9)}_{\color{cyan}{\text{5 factors}}} \nonumber\]
Revoyons le vocabulaire des expressions avec des exposants.
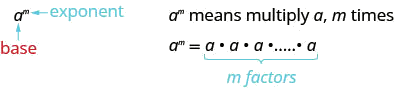
C'est lu\(a\) au\(m^{th}\) pouvoir.
Dans l'expression\(a^m\), l'exposant nous\(m\) indique combien de fois nous utilisons la base\(a\) comme facteur.
Lorsque nous combinons des termes similaires en les additionnant et en les soustrayant, nous devons avoir la même base avec le même exposant. Mais lorsque vous multipliez et divisez, les exposants peuvent être différents, et parfois les bases peuvent également être différentes.
Tout d'abord, nous allons examiner un exemple qui mène à la propriété du produit.
|
\(x^{2} \cdot x^{3}\) |
||
| Qu'est-ce que cela signifie ? |
\(\underbrace{x \cdot x}_{2 factors} \color{cyan}{\cdot} \underbrace{\color{black}{} x\cdot x \cdot x}_{3 factors}\) |
|
| \(x^{5}\) |
Notez que 5 est la somme des exposants 2 et 3. Nous voyons\(x_2 \cdot x_3\) son\(x^{2+3}\) ou\(x^5\).
La base est restée la même et nous avons ajouté les exposants. Cela conduit à la propriété de produit pour les exposants.
Si a est un nombre réel et que\(m\) et\(n\) sont des nombres entiers, alors
\[a^m·a^n=a^{m+n} \nonumber\]
Pour multiplier avec des bases similaires, ajoutez les exposants.
Simplifiez chaque expression :
- \(y^5·y^6\)
- \(2^x·2^{3x}\)
- \(2a^7·3a\).
- Réponse
-
ⓐ
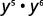
Utilisez la propriété du produit,\(a^m·a^n=a^{m+n}\). 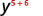
Simplifiez. 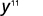
ⓑ
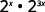
Utilisez la propriété du produit,\(a^m·a^n=a^{m+n}\). 
Simplifiez. 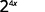
ⓒ
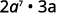
Réécrire,\(a=a^1\). 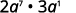
Utilisez la propriété commutative et
utilisez la propriété du produit,\(a^m·a^n=a^{m+n}\).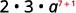
Simplifiez. 
ⓓ
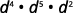
Ajoutez les exposants, car les bases sont les mêmes. 
Simplifiez. 
Simplifiez chaque expression :
- \(b^9·b^8\)
- \(4^{2x}·4^x\)
- \(3p^5·4p\)
- \(x^6·x^4·x^8\).
- Réponse
-
ⓐ\(b^{17}\) ⓑ\(4^{3x}\) ⓒ\(12p^6\)
ⓓ\(x^{18}\)
Simplifiez chaque expression :
- \(x^{12}·x4\)
- \(10·10^x\)
- \(2z·6z^7\)
- \(b^5·b^9·b^5\).
- Répondez à
-
\(x^{16}\)
- Réponse b
-
\(10^{x+1}\)
- Réponse c
-
\(12z^8\)
- Réponse d
-
\(b^{19}\)
Nous allons maintenant examiner une propriété d'exposant pour la division. Comme précédemment, nous allons essayer de découvrir une propriété à l'aide de quelques exemples.
| Considérez | \(\dfrac{x^5}{x^2}\) | et | \(\dfrac{x^2}{x^3}\) |
| Qu'est-ce qu'ils veulent dire ? | \(\dfrac{x·x·x·x·x}{x·x}\) | \(\dfrac{x·x}{x·x·x}\) | |
| Utilisez la propriété Fractions équivalentes. | \(\dfrac{\cancel{x}·\cancel{x}·x·x·x}{\cancel{x}·\cancel{x}}\) | \(\dfrac{\cancel{x}·\cancel{x}·1}{\cancel{x}·\cancel{x}·x}\) | |
| Simplifiez. | \(x^3\) |
\(\dfrac{1}{x}\) |
Remarquez que dans chaque cas, les bases étaient les mêmes et nous avons soustrait des exposants. Nous voyons\(\dfrac{x^5}{x^2}\) son\(x^{5−2}\) ou\(x^3\). Nous voyons\(\dfrac{x^2}{x^3}\) son ou\(\dfrac{1}{x}\). Lorsque le plus grand exposant se trouvait dans le numérateur, il nous restait des facteurs dans le numérateur. Lorsque le plus grand exposant se trouvait dans le dénominateur, il ne nous restait que des facteurs dans le dénominateur : notez le numérateur de 1. Lorsque tous les facteurs du numérateur ont été supprimés, n'oubliez pas que cela divise réellement les facteurs en un, et nous avons donc besoin d'un 1 dans le numérateur. \(\dfrac{\cancel{x}}{\cancel{x}}=1\). Cela conduit à la propriété du quotient pour les exposants.
Si\(a\) est un nombre réel\(a \neq 0\), et\(m\) et\(n\) sont des nombres entiers, alors
\[ \begin{array} {lllll} {\dfrac{a^m}{a^n}=a^{m−n},} &{m>n} &{\text{and}} &{\dfrac{a^m}{a^n}=\dfrac{1}{a^{n−m}},} &{n>m} \\ \nonumber \end{array} \]
Simplifiez chaque expression :
- \(\dfrac{x^9}{x^7}\)
- \(\dfrac{3^{10}}{3^2}\)
- \(\dfrac{b^8}{b^{12}}\)
- \(\dfrac{7^3}{7^5}\).
- Réponse
-
Pour simplifier une expression avec un quotient, nous devons d'abord comparer les exposants du numérateur et du dénominateur.
ⓐ
Depuis\(9>7\), il y a plus de facteurs\(x\) dans le numérateur. 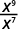
Utilisez la propriété du quotient,\(\dfrac{a^m}{a^n}=a^{m−n}\). 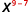
Simplifiez. 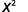
ⓑ
Depuis\(10>2\), il y a plus de facteurs\(3\) dans le numérateur. 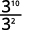
Utilisez la propriété du quotient,\(\dfrac{a^m}{a^n}=a^{m−n}\). 
Simplifiez. 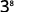
Notez que lorsque le plus grand exposant se trouve dans le numérateur, il nous reste des facteurs dans le numérateur.
ⓒ
Depuis\(12>8\), il y a plus de facteurs bb dans le dénominateur. 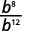
Utilisez la propriété du quotient,\(\dfrac{a^m}{a^n}=a^{m−n}\). 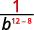
Simplifiez. 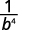
ⓓ
Depuis\(5>3\), il y a plus de facteurs\(3\) dans le dénominateur. 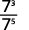
Utilisez la propriété du quotient,\(\dfrac{a^m}{a^n}=a^{m−n}\). 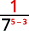
Simplifiez. 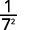
Simplifiez. 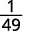
Notez que lorsque le plus grand exposant se trouve dans le dénominateur, il nous reste des facteurs dans le dénominateur.
Simplifiez chaque expression :
- \(\dfrac{x^{15}}{x^{10}}\)
- \(\dfrac{6^{14}}{6^5}\)
- \(\dfrac{x^{18}}{x^{22}}\)
- \(\dfrac{12^{15}}{12^{30}}\).
- Réponse
-
ⓐ\(x^5\)
ⓑ\(6^9\)
ⓒ\(\dfrac{1}{x^4}\)
ⓓ\(\dfrac{1}{12^{15}}\)
Simplifiez chaque expression :
- \(\dfrac{y^{43}}{y^{37}}\)
- \(\dfrac{10^{15}}{10^{7}}\)
- \(\dfrac{m^7}{m^{15}}\)
- \(\dfrac{9^8}{9^{19}}\).
- Réponse
-
ⓐ\(y_6\)
ⓑ\(108\)
ⓒ\(1m8\)
ⓓ\(\dfrac{1}{9^{11}}\)
Un cas particulier de la propriété du quotient est celui où les exposants du numérateur et du dénominateur sont égaux, comme dans le cas d'une expression telle que\(\dfrac{a^m}{a^m}\). Nous savons\(\dfrac{x}{x}=1\), pour tous,\(x(x\neq 0)\) puisque tout nombre divisé par lui-même est 1.
La propriété du quotient pour les exposants nous montre comment simplifier\(\dfrac{a^m}{a^m}\). quand\(m>n\) et quand n<mn<m en soustrayant les exposants. Et si\(m=n\) ? Nous allons simplifier de deux\(\dfrac{a^m}{a^m}\) manières pour nous amener à la définition de la propriété d'exposant zéro. En général, pour\(a \neq 0\) :
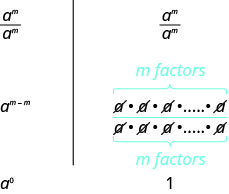
Nous voyons des\(\dfrac{a^m}{a^m}\) simplifications vers\(a^0\) et vers 1. Donc\(a^0=1\). Toute base différente de zéro portée à la puissance zéro est égale\(1\).
Si\(a\) c'est un nombre différent de zéro, alors\(a^0=1\).
Si\(a\) est un nombre différent de zéro, alors\(a\) à la puissance de zéro est égal à\(1\).
Tout nombre différent de zéro élevé à la puissance zéro est\(1\).
Dans ce texte, nous supposons que toute variable que nous élevons à la puissance zéro n'est pas nulle.
Simplifiez chaque expression : ⓐ\(9^0\) ⓑ\(n^0\).
- Réponse
-
La définition indique que tout nombre différent de zéro élevé à la puissance zéro est\(1\).
ⓐ Utilisez la définition de l'exposant zéro. \(9^0 = 1\)
ⓑ Utilisez la définition de l'exposant zéro. \(n^0 = 1\)
Pour simplifier l'expression\(n\) portée à la puissance nulle, nous utilisons simplement la définition de l'exposant zéro. Le résultat est\(1\).
Simplifiez chaque expression : ⓐ\(11^0\) ⓑ\(q^0\).
- Réponse
-
ⓐ 1
ⓑ 1
Simplifiez chaque expression : ⓐ\(23^0\) ⓑ\(r^0\).
- Réponse
-
ⓐ 1
ⓑ 1
Utiliser la définition d'un exposant négatif
Nous avons vu que la propriété du quotient pour les exposants a deux formes selon que l'exposant est plus grand au numérateur ou au dénominateur. Et si nous soustrayions simplement les exposants, quel que soit le plus grand ?
Considérons\(\dfrac{x^2}{x^5}\). Nous soustrayons l'exposant du dénominateur de l'exposant du numérateur. Nous voyons\(\dfrac{x^2}{x^5}\) son\(x^{2−5}\) ou\(x^{−3}\).
Nous pouvons également simplifier\(\dfrac{x^2}{x^5}\) en divisant les facteurs communs :
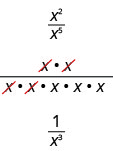
Cela implique cela\(x^{−3}=\dfrac{1}{x^3}\) et cela nous amène à la définition d'un exposant négatif. Si n est un entier et\(a\neq 0\), alors\(a^{−n}=\dfrac{1}{a^n}\).
Voyons maintenant ce qu'il advient d'une fraction dont le numérateur est un et dont le dénominateur est un entier élevé à un exposant négatif.
\( \begin{array} {ll} {} &{\dfrac{1}{a^{-n}}} \\ {} &{} \\ {\text{Use the definition of a negative exponent, } a^{-n}= \dfrac{1}{a^n}} &{\dfrac{1}{\dfrac{1}{a^n}}} \\ {} &{} \\ {\text{Simplify the complex fraction.}} &{1·\dfrac{a^n}{1}} \\ {} &{} \\ {\text{Multiply.}} &{a^n} \\ \end{array} \)
Cela implique\(\dfrac{1}{a^{−n}}=a^n\) et constitue une autre forme de définition des propriétés des exposants négatifs.
Si\(n\) est un entier et\(a\neq 0\), alors\(a^{−n}=\dfrac{1}{a^n}\) ou\(\dfrac{1}{a^{−n}}=a^n\).
L'exposant négatif nous indique que nous pouvons réécrire l'expression en prenant l'inverse de la base puis en changeant le signe de l'exposant.
Toute expression qui possède des exposants négatifs n'est pas considérée comme étant sous sa forme la plus simple. Nous utiliserons la définition d'un exposant négatif et d'autres propriétés des exposants pour écrire l'expression avec uniquement des exposants positifs.
Par exemple, si après avoir simplifié une expression, nous obtenons l'expression\(x^{−3}\), nous ferons une étape supplémentaire et écrirons\(\dfrac{1}{x^3}\). La réponse est considérée comme étant dans sa forme la plus simple lorsqu'elle ne comporte que des exposants positifs.
Simplifiez chaque expression : ⓐ\(x^{−5}\) ⓑ\(10^{−3}\) ⓒ\(\dfrac{1}{y^{−4}}\) ⓓ\(13^{−2}\).
- Réponse
-
ⓐ
\(\begin{array} {ll} {} &{x^{−5}} \\ {\text{Use the definition of a negative exponent, } a^{−n}=\dfrac{1}{a^n}.} &{\dfrac{1}{x^5}} \\ \end{array}\)
ⓑ
\(\begin{array} {ll} {} &{10^{-3}} \\ {\text{Use the definition of a negative exponent, }a^{−n}=\dfrac{1}{a^n}.} &{\dfrac{1}{10^3}} \\ {\text{Simplify.}} &{\dfrac{1}{1000}} \\ \end{array}\)
ⓒ
\(\begin{array} {ll} {} &{\dfrac{1}{y^{-4}}} \\ {\text{Use the property of a negative exponent, } \dfrac{1}{a^{−n}}=a^n.} &{y^4} \\ \end{array}\)
ⓓ
\(\begin{array} {ll} {} &{\dfrac{1}{3^{-2}}} \\ {\text{Use the property of a negative exponent, } \dfrac{1}{a^{−n}}=a^n.} &{3^2} \\ {\text{Simplify.}} &{9} \\ \end{array}\)
Simplifiez chaque expression : ⓐ\(z^{−3}\) ⓑ\(10^{−7}\) ⓒ\(\dfrac{1}{p^{−8}}\) ⓓ\(\dfrac{1}{4^{−3}}\).
- Réponse
-
ⓐ\(\dfrac{1}{z^3}\) ⓑ\(\dfrac{1}{10^7}\) ⓒ\(p^8\) ⓓ\(64\)
Simplifiez chaque expression : ⓐ\(n^{−2}\) ⓑ\(10^{−4}\) ⓒ\(\dfrac{1}{q^{−7}}\) ⓓ\(\dfrac{1}{2^{−4}}\).
- Réponse
-
ⓐ\(\dfrac{1}{n^2}\) ⓑ\(\dfrac{1}{10,000}\) ⓒ\(q^7\)
ⓓ\(16\)
Supposons maintenant que nous ayons une fraction élevée à un exposant négatif. Utilisons notre définition des exposants négatifs pour nous mener à une nouvelle propriété.
\(\begin{array} {ll} {} &{\left( \dfrac{3}{4} \right)^{-2}} \\ {} &{} \\ {\text{Use the definition of a negative exponent, } a^{−n}=\dfrac{1}{a^n}.} &{\dfrac{1}{\left( \dfrac{3}{4} \right)^{2}}} \\ {} &{} \\ {\text{Simplify the denominator.}} &{\dfrac{1}{\dfrac{9}{16}}} \\{} &{} \\ {\text{Simplify the complex fraction.}} &{\dfrac{16}{9}} \\ {} &{} \\ {\text{But we know that }\dfrac{16}{9}\text{ is } \left( \dfrac{4}{3} \right)^{2}.} &{} \\ {\text{This tells us that}} &{\left( \dfrac{3}{4} \right)^{-2} = \left( \dfrac{4}{3} \right)^{2}} \\ \end{array} \)
Pour passer de la fraction initiale élevée à un exposant négatif au résultat final, nous avons pris l'inverse de la base, la fraction, et avons changé le signe de l'exposant.
Cela nous amène au quotient d'une propriété de puissance négative.
Si\(a\) et\(b\) sont des nombres réels\(a\neq 0\),\(b\neq 0\) et\(n\) est un entier, alors
\[\left(\dfrac{a}{b}\right)^{−n}=\left(\dfrac{b}{a}\right)^n \nonumber \].
Simplifiez chaque expression : ⓐ\(\left( \dfrac{5}{7} \right)^{−2}\) ⓑ\(\left( −\dfrac{x}{y} \right)^{−3}\).
- Réponse
-
ⓐ
\(\begin{array} {ll} {} &{\left( \dfrac{5}{7}\right)^{-2}} \\ {\text{Use the Quotient to a Negative Exponent Property, } \left(\dfrac{a}{b} \right)^{−n}= \left( \dfrac{b}{a} \right)^n.} &{} \\ {\text{Take the reciprocal of the fraction and change the sign of the exponent.}} &{\left( \dfrac{7}{5}\right)^2} \\ {\text{Simplify.}} &{\dfrac{49}{25}} \\ \end{array} \)
ⓑ
\(\begin{array} {ll} {} &{\left( -\dfrac{x}{y}\right)^{-3}} \\ {\text{Use the Quotient to a Negative Exponent Property, } \left(\dfrac{a}{b} \right)^{−n}= \left( \dfrac{b}{a} \right)^n.} &{} \\ {\text{Take the reciprocal of the fraction and change the sign of the exponent.}} &{\left( -\dfrac{y}{x}\right)^3} \\ {\text{Simplify.}} &{-\dfrac{y^3}{x^3}} \\ \end{array} \)
Simplifiez chaque expression : ⓐ\(\left(\dfrac{2}{3}\right)^{−4}\) ⓑ\(\left(−\dfrac{m}{n}\right)^{−2}\).
- Réponse
-
ⓐ\(\dfrac{81}{16}\) ⓑ\(\dfrac{n^2}{m^2}\)
Simplifiez chaque expression : ⓐ\(\left(\dfrac{3}{5}\right)^{−3}\) ⓑ\(\left(−\dfrac{a}{b}\right)^{−4}\).
- Réponse
-
ⓐ\(\dfrac{125}{27}\) ⓑ\(\dfrac{b^4}{a^4}\)
Maintenant que nous avons des exposants négatifs, nous allons utiliser la propriété du produit avec des expressions qui ont des exposants négatifs.
Simplifiez chaque expression : ⓐ\(z^{−5}·z^{−3}\) ⓑ\((m^4n^{−3})(m^{−5}n^{−2})\) ⓒ\((2x^{−6}y^8)(−5x^5y^{−3})\).
- Réponse
-
ⓐ
\(\begin{array} {ll} {} &{z^{−5}·z^{−3}} \\ {\text{Add the exponents, since the bases are the same.}} &{z^{−5−3}} \\ {\text{Simplify.}} &{z^{−8}} \\ {\text{Use the definition of a negative exponent.}} &{\dfrac{1}{z^8}} \\ \end{array} \)
ⓑ
\(\begin{array} {ll} {} &{(m^4n^{−3})(m^{−5}n^{−2})} \\ {\text{Use the Commutative Property to get like}} &{} \\ {\text{bases together.}} &{m^4m^{−5}·n^{−2}n^{−3}} \\ {\text{Add the exponents for each base.}} &{m^{−1}·n^{−5}} \\ {\text{Take reciprocals and change the signs of the exponents.}} &{\dfrac{1}{m^1}·\dfrac{1}{n^5}} \\ {\text{Simplify.}} &{\dfrac{1}{mn^5}} \\ \end{array} \)
ⓒ
\(\begin{array} {ll} {} &{(2x^{−6}y^8)(−5x^5y^{−3})} \\ {\text{Rewrite with the like bases together.}} &{2(−5)·(x^{−6}x^5)·(y^8y^{−3})} \\ {\text{Multiply the coefficients and add the exponents}} &{} \\ {\text{of each variable.}} &{−10·x^{−1}·y5} \\ {\text{Use the definition of a negative exponent,} a^{−n}=\dfrac{1}{a^n}.} &{−10·\dfrac{1}{x}·y^5} \\ {\text{Simplify.}} &{−10y^5x} \\ \end{array} \)
Simplifiez chaque expression :
ⓐ\(z^{−4}·z^{−5}\) ⓑ\((p^6q^{−2})(p^{−9}q^{−1})\) ⓒ\((3u^{−5}v^7)(−4u^4v^{−2})\).
- Réponse
-
ⓐ\(\dfrac{1}{z^9}\) ⓑ\(\dfrac{1}{p^3q^3}\) ⓒ\(−\dfrac{12v^5}{u}\)
Simplifiez chaque expression :
ⓐ\(c^{−8}·c^{−7}\) ⓑ\((r^5s^{−3})(r^{−7}s^{−5})\) ⓒ\((−6c^{−6}d^4)(−5c^{−2}d^{−1})\).
- Réponse
-
ⓐ\(\dfrac{1}{c^15}\) ⓑ\(\dfrac{1}{r^2s^8}\) ⓒ\(\dfrac{30d^3}{c^8}\)
Examinons maintenant une expression exponentielle qui contient une puissance portée à une puissance. Voyez si vous pouvez découvrir une propriété générale.
\(\begin{array} {ll} {} &{(x^2)^3} \\ {\text{What does this mean?}} &{x^2·x^2·x^2} \\ \end{array} \)
| Combien de facteurs au total ? | 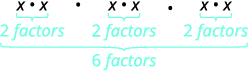 |
| Nous avons donc | 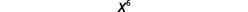 |
Remarquez que le 6 est le produit des exposants 2 et 3. Nous voyons que\((x^2)^3\) c'est\(x^{2·3}\) ou\(x^6\).
Nous avons multiplié les exposants. Cela conduit à la propriété Power pour les exposants.
Si\(a\) est un nombre réel et que\(m\) et\(n\) sont des nombres entiers, alors
\[(a^m)^n=a^{m·n} \nonumber \]
Pour élever une puissance à une puissance, multipliez les exposants.
Simplifiez chaque expression : ⓐ\((y^5)^9\) ⓑ\((4^4)^7\) ⓒ\((y^3)^6(y^5)^4\).
- Réponse
-
ⓐ
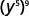
Utilisez la propriété Power,\((a^m)^n=a^{m·n}\). 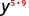
Simplifiez. 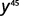
ⓑ
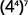
Utilisez la propriété Power. 
Simplifiez. 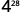
ⓒ
\(\begin{array} {ll} {} &{(y^3)^6(y^5)^4} \\ {\text{Use the Power Property.}} &{y^{18}·y^{20}} \\ {\text{Add the exponents.}} &{y^{38}} \\ \end{array} \)
Simplifiez chaque expression : ⓐ\((b^7)^5\) ⓑ\((5^4)^3\) ⓒ\((a^4)^5(a^7)^4\).
- Réponse
-
ⓐ\(b^{35}\) ⓑ\(5^{12}\) ⓒ\(a^{48}\)
Simplifiez chaque expression : ⓐ\((z^6)^9\) ⓑ\((3^7)^7\) ⓒ\((q^4)^5(q^3)^3\).
- Réponse
-
ⓐ\(z^{54}\) ⓑ\(3^{49}\) ⓒ\(q^{29}\)
Nous allons maintenant examiner une expression contenant un produit qui est élevé à une puissance. Pouvez-vous trouver ce modèle ?
\(\begin{array} {ll} {} &{(2x)^3} \\ {\text{What does this mean?}} &{2x·2x·2x} \\ {\text{We group the like factors together.}} &{2·2·2·x·x·x} \\ {\text{How many factors of 2 and of }}x &{2^3·x^3} \\ \end{array} \)
Remarquez que chaque facteur a été élevé au pouvoir et\((2x)^3\) qu'il est\(2^3·x^3\).
L'exposant s'applique à chacun des facteurs ! Cela conduit au produit à une propriété de puissance pour les exposants.
Si\(a\) et\(b\) sont des nombres réels et\(m\) sont un nombre entier, alors
\[(ab)^m=a^mb^m \nonumber \]
Pour élever un produit à une puissance, augmentez chaque facteur à cette puissance.
Simplifiez chaque expression : ⓐ\((−3mn)^3\) ⓑ\((−4a^2b)^0\) ⓒ\((6k^3)^{−2}\) ⓓ\((5x^{−3})^2\).
- Réponse
-
ⓐ
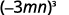
Utiliser la puissance d'une propriété du produit,\((ab)^m=a^mb^m\). 
Simplifiez. 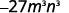
ⓑ
\(\begin{array} {ll} {} &{(−4a^2b)^0} \\ {\text{Use Power of a Product Property, }(ab)^m=a^mb^m.} &{(−4)^0(a^2)^0(b)^0} \\ {\text{Simplify.}} &{1·1·1} \\ {\text{Multiply.}} &{1} \\ \end{array} \)
ⓒ
\(\begin{array} {ll} {} &{(6k^3)^{−2}} \\ {\text{Use Power of a Product Property, }(ab)^m=a^mb^m.} &{(6)^{−2}(k^3)^{−2}} \\ {\text{Use the Power Property, }(a^m)^n=a^{m·n}.} &{6^{−2}k^{−6}} \\ {\text{Use the Definition of a negative exponent, }a^{−n}=\dfrac{1}{a^n}.} &{\dfrac{1}{6^2}·\dfrac{1}{k^6}} \\ {\text{Simplify.}} &{\dfrac{1}{36k^6}} \\ \end{array} \)
ⓓ
\(\begin{array} {ll} {} &{(5x^{−3})^2} \\ {\text{Use Power of a Product Property, }(ab)^m=a^mb^m.} &{5^2(x^{−3})^2} \\ {\text{Simplify.}} &{25·x^{−6}} \\ {\text{Rewrite }x−6 \text{using, }a^{−n}=\text{1}{a^n}.} &{25·\dfrac{1}{x^6}} \\ {\text{Simplify.}} &{\dfrac{25}{x^6}} \\ \end{array} \)
Simplifiez chaque expression : ⓐ\((2wx)^5\) ⓑ\((−11pq3)^0\) ⓒ\((2b^3)^{−4}\) ⓓ\((8a^{−4})^2\).
- Réponse
-
ⓐ\(32w^5x^5\) ⓑ 1 ⓒ\(\dfrac{1}{16b^{12}}\)
ⓓ\(\dfrac{64}{a^8}\)
Simplifiez chaque expression : ⓐ\((−3y)^3\) ⓑ\((−8m^2n^3)^0\) ⓒ\((−4x^4)^{−2}\) ⓓ\((2c^{−4})^3\).
- Réponse
-
ⓐ\(−27y^3\) ⓑ 1 ⓒ\(\dfrac{1}{16x^8}\)
ⓓ\(8c^{12}\)
Nous allons maintenant examiner un exemple qui nous mènera au quotient d'une propriété énergétique.
\( \begin{array} {ll} {} &{\left( \dfrac{x}{y}\right)^3} \\ {\text{This means}} &{\dfrac{x}{y}·\dfrac{x}{y}·\dfrac{x}{y}} \\ {\text{Multiply the fractions.}} &{\dfrac{x·x·x}{y·y·y}} \\ {\text{Write with exponents.}} &{\dfrac{x^3}{y^3}} \\ \end{array} \)
Notez que l'exposant s'applique à la fois au numérateur et au dénominateur.
Nous voyons que c'\(\left(\dfrac{x}{y}\right)^3\)est le cas\(\dfrac{x^3}{y^3}\).
Cela conduit au quotient d'une propriété de puissance pour les exposants.
Si\(a\) et\(b\) sont des nombres réels\(b\neq 0\), et\(m\) est un entier, alors
\[\left(\dfrac{a}{b}\right)^m=\dfrac{a^m}{b^m} \nonumber \]
Pour élever une fraction à une puissance, augmentez le numérateur et le dénominateur à cette puissance.
Simplifiez chaque expression :
ⓐ\(\left(\dfrac{b}{3}\right)^4\) ⓑ\(\left(\dfrac{k}{j}\right)^{−3}\) ⓒ\(\left(\dfrac{2xy^2}{z}\right)^3\) ⓓ\(\left(\dfrac{4p^{−3}}{q^2}\right)^2\).
- Réponse
-
ⓐ
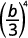
Utilisez le quotient pour une propriété de puissance,\((ab)^m=a^mb^m\). 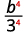
Simplifiez. 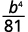
ⓑ
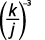
Augmentez le numérateur et le dénominateur à la puissance. 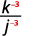
Utilisez la définition d'un exposant négatif. 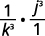
Multipliez. 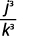
ⓒ
\(\begin{array} {ll} {} &{\left(\dfrac{2xy^2}{z}\right)^3} \\ {\text{Use Quotient to a Power Property, }\left(\dfrac{a}{b}\right)^m=\dfrac{a^m}{b^m}.} &{\dfrac{(2xy^2)^3}{z^3}} \\ {\text{Use the Product to a Power Property, }(ab)^m=a^mb^m.} &{\dfrac{8x^3y^6}{z^3}} \\ \end{array} \)
ⓓ
\(\begin{array} {ll} {} &{\left(\dfrac{4p^{−3}}{q^2}\right)^2} \\ {\text{Use Quotient to a Power Property, }\left(\dfrac{a}{b}\right)^m=\dfrac{a^m}{b^m}.} &{\dfrac{(4p^{−3})^2}{(q^2)^2}} \\ {\text{Use the Product to a Power Property, }(ab)^m=a^mb^m.} &{\dfrac{4^2(p^{−3})^2}{(q^2)^2}} \\ {\text{Simplify using the Power Property, }(a^m)^n=a^{m·n}.} &{\dfrac{16p^{−6}}{q^4}} \\ {\text{Use the definition of negative exponent.}} &{\dfrac{16}{q^4}·\dfrac{1}{p^6}} \\ {\text{Simplify.}} &{\dfrac{16}{p^6q^4}} \\ \end{array} \)
Simplifiez chaque expression :
ⓐ\(\left(\dfrac{p}{10}\right)^4\) ⓑ\(\left(\dfrac{m}{n}\right)^{−7}\) ⓒ\(\left(\dfrac{3ab^3}{c^2}\right)^4\) ⓓ\(\left(\dfrac{3x^{−2}}{y^3}\right)^3\).
- Réponse
-
ⓐ\(\dfrac{p^4}{10000}\) ⓑ\(\dfrac{n^7}{m^7}\)
ⓒ\(\dfrac{81a^4b^{12}}{c^8}\) ⓓ\(\dfrac{27}{x^6y^9}\)
Simplifiez chaque expression :
ⓐ\(\left(\dfrac{−2}{q}\right)^3\) ⓑ\(\left(\dfrac{w}{x}\right)^{−4}\) ⓒ\(\left(\dfrac{xy^3}{3z^2}\right)^2\) ⓓ\(\left(\dfrac{2m^{−2}}{n^{−2}}\right)^3\).
- Réponse
-
ⓐ\(\dfrac{−8}{q^3}\) ⓑ\(\dfrac{x^4}{w^4}\) ⓒ\(\dfrac{x^2y^6}{9z^4}\)
ⓓ\( \dfrac{8n^6}{m^6}\)
Nous avons maintenant plusieurs propriétés pour les exposants. Résumons-les, puis nous donnerons d'autres exemples utilisant plus d'une des propriétés.
Si\(a\) et\(b\) sont des nombres réels, et\(m\) et\(n\) sont des nombres entiers, alors
| Propriété | Désignation |
|---|---|
| Propriété du produit | \(a^m·a^n=a^{m+n}\) |
| Propriété énergétique | \((a^m)^n=a^{m·n}\) |
| Du produit à une puissance | \((ab)^n=a^nb^n\) |
| Propriété du quotient | \(\dfrac{a^m}{a^n}=a^{m−n},a\neq 0\) |
| Propriété d'exposant zéro | \(a^0=1,a \neq 0\) |
| Quotient par rapport à une propriété énergétique | \(\left(\dfrac{a}{b}\right)^m=\dfrac{a^m}{b^m},b \neq 0 \) |
| Propriétés des exposants négatifs | \(a^{−n}=\dfrac{1}{a^n}\)et\(\dfrac{1}{a^{−n}}=a^n\) |
| Quotient par rapport à un exposant négatif | \(\left(\dfrac{a}{b}\right)^{−n}=\left(\dfrac{b}{a}\right)^n\) |
Simplifiez chaque expression en appliquant plusieurs propriétés :
ⓐ\((3x^2y)^4(2xy^2)^3\) ⓑ\(\dfrac{(x^3)^4(x^{−2})^5}{(x^6)^5}\) ⓒ\(\left(\dfrac{2xy^2}{x^3y^{−2}}\right)^2 \left(\dfrac{12xy^3}{x^3y^{−1}}\right)^{−1}\).
- Réponse
-
ⓐ
\(\begin{array} {ll} {} &{(3x^2y)^4(2xy^2)^3} \\ {} &{} \\ {\text{Use the Product to a Power Property, }(ab)^m=a^mb^m.} &{(3^4x^8y^4)(2^3x^3y^6)} \\ {} &{} \\ {\text{Simplify.}} &{(81x^8y^4)(8x^3y^6)} \\ {} &{} \\ {\text{Use the Commutative Property.}} &{81·8·x^8·x^3·y^4·y^6} \\ {} &{} \\ {\text{Multiply the constants and add the exponents.}} &{648x^{11}y^{10}} \\ \end{array} \)
ⓑ
\( \begin{array} {ll} {} &{\dfrac{(x^3)^4(x^{−2})^5}{(x^6)^5}} \\ {\text{Use the Power Property, }(a^m)^n=a^{m·n}.} &{(x^{12})(x^{−10})(x^{30})} \\ {\text{Add the exponents in the numerator.}} &{\dfrac{x^2}{x^{30}}} \\ {\text{Use the Quotient Property, }\dfrac{a^m}{a^n}=\dfrac{1}{a^{n−m}}.} &{\dfrac{1}{x^{28}}} \\ \end{array} \)
ⓒ
\( \begin{array} {ll} {} &{\left(\dfrac{2xy^2}{x^3y^{−2}}\right)^2 \left(\dfrac{12xy^3}{x^3y^{−1}}\right)^{−1}} \\ {\text{Simplify inside the parentheses first.}} &{\left(\dfrac{2y^4}{x^2}\right)^2\left(\dfrac{12y^4}{x^2}\right)^{−1}} \\ {\text{Use the Quotient to a Power Property, }\left(\dfrac{a}{b}\right)^m=\dfrac{a^m}{b^m}.} &{\dfrac{(2y^4)^2}{(x^2)^2}\dfrac{(12y^4)^{−1}}{(x^2)^{−1}}} \\ {\text{Use the Product to a Power Property, }(ab)^m=a^mb^m.} &{\dfrac{4y^8}{x^4}·\dfrac{12^{−1}y^{−4}}{x^{−2}}} \\ {\text{Simplify.}} &{\dfrac{4y^4}{12x^2}} \\ {\text{Simplify.}} &{\dfrac{y^4}{3x^2}} \\ \end{array} \)
Simplifiez chaque expression :
ⓐ\((c^4d^2)^5(3cd^5)^4\) ⓑ\(\dfrac{(a^{−2})^3(a^2)^4}{(a^4)^5}\) ⓒ\(\left(\dfrac{3xy^2}{x^2y^{−3}}\right)^2\)
- Réponse
-
ⓐ\(81c^{24}d^{30}\) ⓑ\(\dfrac{1}{a^{18}}\)
ⓒ\(\dfrac{9y^{10}}{x^2}\)
Simplifiez chaque expression :
ⓐ\((a^3b^2)^6(4ab^3)^4\) ⓑ\(\dfrac{(p^{−3})^4(p^5)^3}{(p^7)^6}\) ⓒ\(\left(\dfrac{4x^3y^2}{x^2y^{−1}}\right)^2\left(\dfrac{8xy^{−3}}{x^2y}\right)^{−1}\).
- Réponse
-
ⓐ\(256a^{22}b^{24}\) ⓑ\(\dfrac{1}{p^{39}}\)
ⓒ\(2x^3y^{10}\)
Utiliser la notation scientifique
Travailler avec des nombres très grands ou très petits peut être gênant. Comme notre système de numérotation est basé sur dix, nous pouvons utiliser des puissances de dix pour réécrire des nombres très grands ou très petits afin de les rendre plus faciles à utiliser. Considérez les nombres 4 000 et 0,004.
En utilisant la valeur de position, nous pouvons réécrire les nombres 4 000 et 0,004. Nous savons que 4 000 signifie\(4\times1,000\) et 0,004 signifie\(4\times\dfrac{1}{1,000}\).
Si nous écrivons les 1 000 comme une puissance de dix sous forme exponentielle, nous pouvons réécrire ces nombres de la manière suivante :
| 4 000 | \(4\times1,000\) | \(4\times103\) | |
| 0,004 | \(4\times\dfrac{1}{1,000}\) | \(4\times\dfrac{1}{103}\) | \(4\times10^{−3}\) |
Lorsqu'un nombre est écrit comme le produit de deux nombres, où le premier facteur est un nombre supérieur ou égal à un mais inférieur à dix, et le second facteur est une puissance de 10 écrite sous forme exponentielle, on dit que c'est en notation scientifique.
Un nombre est exprimé en notation scientifique lorsqu'il est de la forme
\[\begin{array} {llllllllllll} {a} &{\times} &{10^n} &{\text{where}} &{1} &{\leq} &{a} &{<} &{10} &{\text{and}} &{n} &{\text{is an integer.}} \\ \nonumber \end{array}\]
Il est habituel en notation scientifique de l'utiliser comme signe de\(\times\) multiplication, même si nous évitons d'utiliser ce signe ailleurs en algèbre.
Si nous examinons ce qui est arrivé à la virgule décimale, nous pouvons voir une méthode permettant de passer facilement de la notation décimale à la notation scientifique.

Dans les deux cas, la décimale a été déplacée de 3 places pour obtenir le premier facteur entre 1 et 10.
La puissance de 10 est positive lorsque le nombre est supérieur à\(1: 4,000=4\times10^3\)
La puissance de 10 est négative lorsque le nombre est compris entre 0 et 1 :\(0.004=4\times10^{−3}\)
- Déplacez la virgule décimale de manière à ce que le premier facteur soit supérieur ou égal à 1 mais inférieur à 10.
- Comptez le nombre de décimales sur\(n\) lesquelles le point décimal a été déplacé.
- Écrivez le nombre sous la forme d'un produit d'une puissance de 10. Si le numéro d'origine est.
- supérieure à 1, la puissance de 10 sera\(10^n\).
- entre 0 et 1, la puissance de 10 sera\(10^{−n}\).
- Vérifiez.
Écrivez en notation scientifique : ⓐ\(37,000\) ⓑ\(0.0052\).
- Réponse
-
ⓐ
Le nombre initial, 37 000, est supérieur à 1
donc nous aurons une puissance positive de 10.37 000 Déplacez le point décimal pour obtenir 3,7, un nombre
compris entre 1 et 10.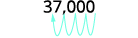
Comptez le nombre de décimales pendant lesquelles le point
a été déplacé.
Écrivez comme un produit d'une puissance de 10. 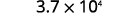
\(\begin{array} {ll} {} &{3.7\times 10^4 } \\ {\text{Check:}} &{3.7 \times 10,000 } \\ {} &{37,000} \\ \end{array} \)
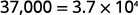
ⓑ
Le nombre d'origine, 0,0052, est compris entre 0
et 1, donc nous aurons une puissance négative de 10.0,0052 Déplacez le point décimal pour obtenir 5,2, un nombre
compris entre 1 et 10.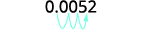
Comptez le nombre de décimales pendant lesquelles le point
a été déplacé.
Écrivez comme un produit d'une puissance de 10. 
\(\begin{array} {ll} {\text{Check:}} &{5.2\times10^{−3}} \\ {} &{5.2\times\dfrac{1}{10^3}} \\ {} &{5.2\times\dfrac{1}{1000}} \\ {} &{5.2\times 0.001} \\ {} &{0.0052} \\ \end{array} \)
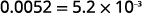
Écrivez en notation scientifique : ⓐ 96 000 ⓑ 0,0078.
- Réponse
-
ⓐ\(9.6\times 10^4\) ⓑ\(7.8\times 10^{−3}\)
Écrivez en notation scientifique : ⓐ 48 300 ⓑ 0,0129.
- Réponse
-
ⓐ\(4.83\times10^4\)
ⓑ\(1.29\times10^{−2}\)
Comment passer de la notation scientifique à la forme décimale ? Regardons deux nombres écrits en notation scientifique et voyons.
\[\begin{array} {lll} {9.12\times10^4} &{} &{9.12\times10^{−4}} \\ {9.12\times10,000} &{} &{9.12\times0.0001} \\ {91,200} &{} &{0.000912} \\ \nonumber \end{array} \]
Si nous examinons l'emplacement de la virgule décimale, nous pouvons voir une méthode simple pour convertir un nombre de la notation scientifique à la forme décimale.

Dans les deux cas, le point décimal s'est déplacé de 4 places. Lorsque l'exposant était positif, la décimale se déplaçait vers la droite. Lorsque l'exposant était négatif, le point décimal se déplaçait vers la gauche.
- Déterminez l'exposant,\(n\), sur le facteur 10.
- Déplacez les\(n\) décimales, en ajoutant des zéros si nécessaire.
- Si l'exposant est positif, déplacez la virgule\(n\) décimale vers la droite.
- Si l'exposant est négatif, déplacez la virgule\(|n|\) décimale vers la gauche.
- Vérifiez.
Convertir au format décimal : ⓐ\(6.2\times10^3\) ⓑ\(−8.9\times 10^{−2}\).
- Réponse
-
ⓐ
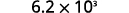
Déterminez l'exposant,\(n\), sur le facteur 10. L'exposant est 3. Puisque l'exposant est positif, déplacez la
virgule décimale de 3 places vers la droite.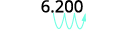
Ajoutez des zéros si nécessaire pour les espaces réservés. 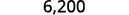
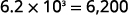
ⓑ

Déterminez l'exposant,\(n\), sur le facteur 10. L'exposant est −2.−2. Comme l'exposant est négatif, déplacez la
virgule décimale de 2 places vers la gauche.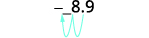
Ajoutez des zéros si nécessaire pour les espaces réservés. 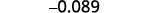
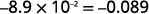
Convertir au format décimal : ⓐ\(1.3\times 10^3\) ⓑ\(−1.2\times 10^{−4}\).
- Réponse
-
ⓐ 1 300 ⓑ\(−0.00012\)
Convertir au format décimal : ⓐ\(−9.5\times 10^4\) ⓑ\(7.5\times 10^{−2}\).
- Réponse
-
ⓐ\(−950,000\) ⓑ 0,075
Lorsque les scientifiques effectuent des calculs avec des nombres très grands ou très petits, ils utilisent la notation scientifique. La notation scientifique permet d'effectuer les calculs sans écrire beaucoup de zéros. Nous verrons comment les propriétés des exposants sont utilisées pour multiplier et diviser des nombres en notation scientifique.
Multipliez ou divisez comme indiqué. Écrivez les réponses sous forme décimale : ⓐ\((−4\times10^5)(2\times10^{−7})\) ⓑ\(\dfrac{9\times10^3}{3\times10^{−2}}\).
- Réponse
-
ⓐ
\(\begin{array} {ll} {} &{(−4\times10^5)(2\times10^{−7})} \\ {\text{Use the Commutative Property to rearrange the factors.}} &{−4·2·10^5·10^{−7}} \\ {\text{Multiply.}} &{−8\times10^{−2}} \\ {} &{} \\ {\text{Change to decimal form by moving the decimal two}} &{} \\ {\text{places left.}} &{−0.08} \\ \end{array}\)
ⓑ
\(\begin{array} {ll} {} &{\dfrac{9\times10^3}{9\times10^{−2}}} \\ {\text{Separate the factors, rewriting as the product of two}} &{} \\ {\text{fractions.}} &{\dfrac{9}{3}\times\dfrac{10^3}{10^{−2}}} \\ {\text{Divide.}} &{3\times10^5} \\ {\text{Change to decimal form by moving the decimal five}} &{} \\ {\text{places right.}} &{300,000} \\ \end{array}\)
Multipliez ou divisez comme indiqué. Écrivez les réponses sous forme décimale :
ⓐ\((−3\times10^5)(2\times10^{−8})\) ⓑ\(\dfrac{8\times10^2}{4\times10^{−2}}\).
- Réponse
-
ⓐ\(−0.006\) ⓑ 20 000
Multipliez ou divisez comme indiqué. Écrivez les réponses sous forme décimale :
ⓐ\((−3\times10^{−2})(3\times10^{−1})\) ⓑ\(\dfrac{8\times10^4}{2\times10^{−1}}\).
- Réponse
-
ⓐ\(−0.009\) ⓑ 400 000
Accédez à ces ressources en ligne pour obtenir des instructions supplémentaires et vous entraîner à utiliser les propriétés de multiplication des exposants.
- Propriétés des exposants
- Exposants négatifs
- Notation scientifique
Concepts clés
- Notation exponentielle
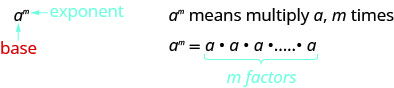
Ceci est lu\(a\) à la\(m^{th}\) puissance.
Dans l'expression\(a^m\), l'exposant nous\(m\) indique combien de fois nous utilisons la base\(a\) comme facteur. - Propriété du produit pour les exposants
Si\(a\) est un nombre réel\(m\) et\(n\) sont des entiers, alors\[a^m·a^n=a^{m+n} \nonumber \]
Pour multiplier avec des bases similaires, ajoutez les exposants. - Propriété de quotient pour les exposants
Si\(a\) est un nombre réel\(a\neq 0\),,\(m\) et et\(n\) sont des entiers, alors\[\begin{array} {lllll} {\dfrac{a^m}{a^n}=a^{m−n},} &{m>n} &{\text{and}} &{\dfrac{a^m}{a^n}=\dfrac{1}{a^{n−m}},} &{n>m}\\ \nonumber \end{array}\]
- Exposant zéro
- Si\(a\) c'est un nombre différent de zéro, alors\(a^0=1\).
- Si\(a\) est un nombre différent de zéro, alors\(a\) à la puissance de zéro est égal à\(1\).
- Tout nombre différent de zéro élevé à la puissance zéro est\(1\).
- Exposant négatif
- Si\(n\) est un entier et\(a\neq 0\), alors\(a^{−n}=\dfrac{1}{a^n}\) ou\(\dfrac{1}{a^{−n}}=a^n\).
- Quotient d'une propriété d'exposant négatif
Si\(a\) et\(b\) sont des nombres réels\(a\neq 0\),,\(b\neq 0\) et\(n\) sont un entier, alors\[(ab)^{−n}=(ba)^n\nonumber \]
- Propriété de puissance pour les exposants
Si\(a\) est un nombre réel\(m\) et\(n\) sont des entiers, alors\[(a^m)^n=a^{m·n}\nonumber \]
Pour élever une puissance à une puissance, multipliez les exposants. - Produit par une propriété de puissance pour les exposants
Si\(a\) et\(b\) sont des nombres réels et\(m\) un nombre entier, alors\[(ab)^m=a^mb^m \nonumber \]
Pour élever un produit à une puissance, augmentez chaque facteur à cette puissance. - Quotient d'une propriété de puissance pour les exposants
Si\(a\) et\(b\) sont des nombres réels\(b\neq0\), et\(m\) est un entier, alors\[\left(\dfrac{a}{b}\right)^m=\dfrac{a^m}{b^m} \nonumber \]
Pour élever une fraction à une puissance, augmentez le numérateur et le dénominateur à cette puissance. - Résumé des propriétés de l'exposant
Si\(a\) et\(b\) sont des nombres réels et que\(m\) et\(n\) sont des entiers, alorsPropriété Désignation Propriété du produit \(a^m·a^n=a^{m+n}\) Propriété énergétique \((a^m)^n=a^{m·n}\) Du produit à une puissance \((ab)^n=a^nb^n\) Propriété du quotient \(\dfrac{a^m}{a^n}=a^{m−n}, a\neq 0\) Propriété d'exposant zéro \(a^0=1,a\neq 0\) Quotient par rapport à une propriété de puissance : \(\left(\dfrac{a}{b}\right)^m=\dfrac{a^m}{b^m}, b\neq 0\) Propriétés des exposants négatifs \(a^{−n}=\dfrac{1}{a^n}\)et\(\dfrac{1}{a^{−n}}=a^n\) Quotient par rapport à un exposant négatif \(\left(\dfrac{a}{b}\right)^{−n}=\left(\dfrac{b}{a}\right)^n\) - Notation scientifique
Un nombre est exprimé en notation scientifique lorsqu'il est de la forme\[a\space\times\space10^n \text{ where }1\leq a<10\text{ and } n \text{ is an integer.} \nonumber \]
- Comment convertir une décimale en notation scientifique.
- Déplacez la virgule décimale de manière à ce que le premier facteur soit supérieur ou égal à 1 mais inférieur à 10.
- Comptez le nombre de décimales sur\(n\) lesquelles le point décimal a été déplacé.
- Écrivez le nombre sous la forme d'un produit d'une puissance de 10. Si le numéro d'origine est.
- supérieure à 1, la puissance de 10 sera\(10^n\).
- entre 0 et 1, la puissance de 10 sera\(10^{−n}\).
- Vérifiez.
- Comment convertir la notation scientifique en forme décimale.
- Déterminez l'exposant,\(n\), sur le facteur 10.
- Déplacez les\(n\) décimales, en ajoutant des zéros si nécessaire.
- Si l'exposant est positif, déplacez la virgule\(n\) décimale vers la droite.
- Si l'exposant est négatif, déplacez la virgule\(|n|\) décimale vers la gauche.
- Vérifiez.
Lexique
- Propriété du produit
- Selon la propriété du produit,\(a\)\(a\) au\(m\) temps\(a\) égal\(a\) au\(m\) plus\(n\).
- Propriété énergétique
- Selon la propriété de puissance,\(a\)\(m\) au\(n\) égal\(a\) aux\(m\) temps\(n\).
- Du produit à une puissance
- Selon le produit d'une propriété de puissance,\(b\) les\(a\) temps entre parenthèses sont\(m\) égaux\(a\)\(b\) aux\(m\) fois au\(m\).
- Propriété du quotient
- Selon la propriété du quotient,\(a\)\(m\) diviser par\(a\) à\(n\) égal\(a\) à\(m\) moins\(n\) tant que ce n'\(a\)est pas zéro.
- Propriété d'exposant zéro
- Selon la propriété Zero Exponent,\(a\) la valeur zéro est\(1\) aussi longue qu'elle n'\(a\)est pas nulle.
- Quotient par rapport à une propriété énergétique
- Selon le quotient d'une propriété de puissance,\(a\) divisé par entre\(b\) parenthèses, la puissance de\(m\) est égale\(a\) à la\(m\) division par\(b\) le\(m\) tant que ce n'\(b\)est pas zéro.
- Propriétés des exposants négatifs
- Selon les propriétés des exposants négatifs,\(a\) au négatif\(n\) est égal\(a\) à\(1\) divisé par\(n\) et\(1\) divisé par\(a\) au négatif\(n\) est égal\(a\) à\(n\).
- Quotient par rapport à un exposant négatif
- L'élévation d'un quotient à un exposant négatif se produit lorsqu'il est\(a\) divisé par entre\(b\) parenthèses à la puissance des\(n\) égaux négatifs\(b\) divisée par entre\(a\) parenthèses à la puissance de\(n\).