10.5E:练习
- Page ID
- 204481
练习成就完美
识别两个变量中二次方程的图
在以下练习中,绘制图表:
\(y=x^2+3\)
- 回答
-
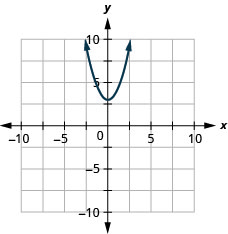
\(y=−x^2+1\)
在以下练习中,确定抛物线是向上还是向下打开。
\(y=−2x^2−6x−7\)
- 回答
-
向下
\(y=6x^2+2x+3\)
y=4x^2+x−4
- 回答
-
向上
\(y=−9x^2−24x−16\)
找到抛物线的对称轴和顶点
在以下练习中,找到 ⓐ 对称轴和 ⓑ 顶点。
\(y=x^2+8x−1\)
- 回答
-
ⓐ x=−4 ⓑ (−4, −17)
\(y=x^2+10x+25\)
\(y=−x^2+2x+5\)
- 回答
-
ⓐ x=1 ⓑ (1,6)
\(y=−2x^2−8x−3\)
找到抛物线的截取点
在以下练习中,找到 x 和 y 截距。
\(y=x^2+7x+6\)
- 回答
-
y: (0,6); x: (−1,0), (−6,0)
\(y=x^2+10x−11\)
\(y=−x^2+8x−19\)
- 回答
-
y: (0, −19); x: 无
\(y=x^2+6x+13\)
\(y=4x^2−20x+25\)
- 回答
-
y: (0,25); x: (52,0)
\(y=−x^2−14x−49\)
两个变量中的图形二次方程
在以下练习中,使用截距、顶点和对称轴绘制图形。
\(y=x^2+6x+5\)
- 回答
-
y: (0,5); x: (−1,0), (−5,0);
轴:x=−3;顶点 :( −3, −4)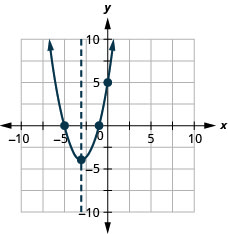
\(y=x^2+4x−12\)
\(y=x^2+4x+3\)
- 回答
-
y: (0,3); x: (−1,0), (−3,0);
轴:x=−2;vertex :( −2, −1)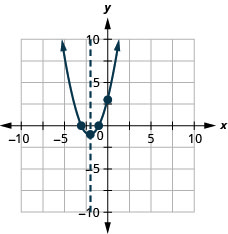
\(y=x^2−6x+8\)
\(y=9x^2+12x+4\)
- 回答
-
y: (0,4); x:\((−\frac{2}{3},0)\);
轴:\((−\frac{2}{3}\); 顶点:\((−\frac{2}{3},0)\)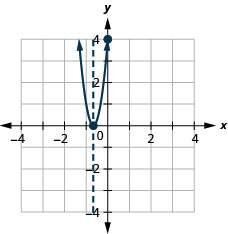
\(y=−x^2+8x−16\)
\(y=−x^2+2x−7\)
- 回答
-
y: (0, −7); x: none; ax
is: x=1; vertex :( 1, −6)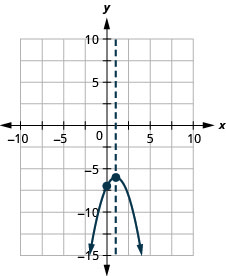
\(y=5x^2+2\)
\(y=2x^2−4x+1\)
- 回答
-
y: (0,1); x: (1.7,0), (0.3,0);
轴:x=1;顶点 :( 1, −1)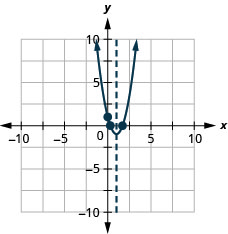
\(y=−4x^2−6x−2\)
\(y=−x^2−4x+2\)
- 回答
-
y: (0,2); x: (−4.4,0), (0.4,0);
轴:x=−2;顶点 :( −2,6)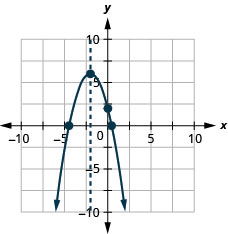
\(y=x^2+6x+8\)
\(y=5x^2−10x+8\)
- 回答
-
y: (0,8);x: 无;
轴:x=1;顶点 :( 1,3)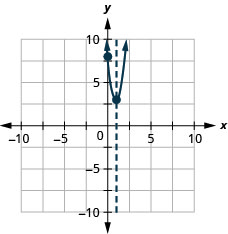
\(y=−16x^2+24x−9\)
\(y=3x^2+18x+20\)
- 回答
-
y: (0,20);x: (−4.5,0),(−1.5,0)
轴:x=−3;vertex :( −3, −7)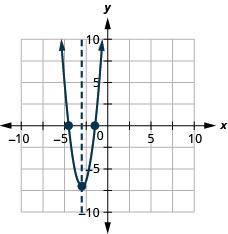
\(y=−2x^2+8x−10\)
求解最大值和最小值应用程序
在以下练习中,找到最大值或最小值。
\(y=2x^2+x−1\)
- 回答
-
最小值为 w\(−\frac{9}{8}\) hen\(x=−\frac{1}{4}\)。
\(y=−4x^2+12x−5\)
\(y=x^2−6x+15\)
- 回答
-
当 x=3 时,最小值为 6。
\(y=−x^2+4x−5\)
\(y=−9x^2+16\)
- 回答
-
当 x=0 时,最大值为 16。
\(y=4x^2−49\)
一支箭从 45 英尺高的平台上以 168 英尺/秒的速度垂直向上射击。 使用二次方程计算\(h=−16t^2+168t+45\)箭头达到其最大高度需要多长时间,然后找到最大高度。
- 回答
-
在 5.3 秒内,箭头将达到 486 英尺的最大高度。
从 20 英尺高的平台上垂直向上投掷一块石头,速度为 160 英尺/秒。 使用二次方程计算\(h=−16t^2+160t+20\)石头达到最大高度需要多长时间,然后找到最大高度。
一家计算机商店老板估计,通过为某台计算机每台收取x美元的费用,他每周可以出售\(40−x\)计算机。 二次方程用于计算当计算机的售价\(R=−x^2+40x\)为 x 时获得的收入 R。找到能给他带来最大收入的销售价格,然后求出最大收入的金额。
- 回答
-
20 台计算机最多可获得 400 美元的收据。
一家销售背包的零售商估计,通过以每件x美元的价格出售\(100−x\)背包,他将能够每月销售背包。 二次方程\(R=−x^2+100x\)用于找出当背包的售价为 x 时收到的 R。找到能给他带来最大收入的卖出价格,然后找到最大收入的金额。
牧场主要在河边围栏的三面围栏。 他需要使用240英尺的围栏最大限度地扩大畜栏面积。 二次方程 A=x (240−2x) 给出了畜栏 A 的面积,表示沿河畜栏的长度 x。 找到沿河畜栏的长度,该长度将给出最大面积,然后找到畜栏的最大面积。
- 回答
-
畜栏河沿岸的长度为120英尺,最大面积为7,200平方英尺。
一位兽医正在他的建筑物旁边封闭一个矩形的户外跑步区,供他照顾的狗使用。 他需要使用 100 英尺的围栏最大限度地扩大面积。 二次方程\(A=x(100−2x)\)给出了狗跑的面积 A,相当于与狗跑接壤的建筑物的长度 x。 找出应与狗跑接壤的建筑物的长度以给出最大面积,然后找到狗跑的最大面积。
日常数学
在上一组练习中,您使用了二次方程\(R=−x^2+40x\),该方程模拟了以 x 美元的价格出售计算机所获得的收入。 您找到了可以提供最大收入的销售价格,并计算了最大收入。 现在,您将了解该模型的更多特征。
1。 绘制方程图\(R=−x^2+40x\)。
2。 找出 x 截距的值。
- 回答
-
1。
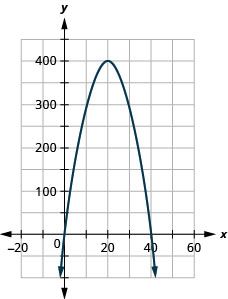
2. (0,0), (40,0)
在前一组练习中,你使用了二次方程\(R=−x^2+100x\),该方程模拟了以 x 美元的价格出售背包所获得的收入。 您找到了可以提供最大收入的销售价格,并计算了最大收入。 现在,您将了解该模型的更多特征。
1。 绘制方程图\(R=−x^2+100x\)。
2. 找出 x 截图的值。
写作练习
自检
a. 完成练习后,使用此清单评估您对本节目标的掌握程度。
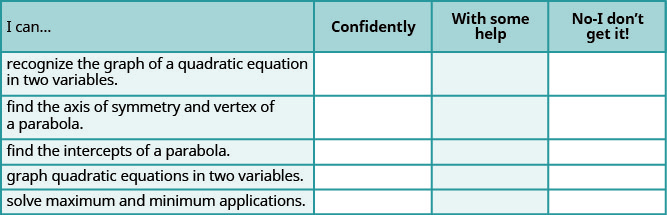
b. 关于你对本部分的掌握程度,这份清单告诉了你什么? 你会采取哪些措施来改进?


