第 10 章复习练习
- Page ID
- 204539
第 10 章复习练习
10.1 使用平方根属性求解二次方程
在以下练习中,使用平方根属性求解。
\(x^2=100\)
- 回答
-
\(x=\pm10\)
\(y^2=144\)
\(m^2−40=0\)
- 回答
-
\(m=\pm2\sqrt{10}\)
\(n^2−80=0\)
\(4a^2=100\)
- 回答
-
\(a=\pm5\)
\(2b^2=72\)
\(r^2+32=0\)
- 回答
-
没有解决办法
\(t^2+18=0\)
\(\frac{4}{3}v^2+4=28\)
- 回答
-
\(v=\pm3\sqrt{2}\)
\(\frac{2}{3}w^2−20=30\)
\(5c^2+3=19\)
- 回答
-
\(c=\pm\frac{4\sqrt{5}}{5}\)
\(3d^2−6=43\)
在以下练习中,使用平方根属性求解。
\((p−5)^2+3=19\)
- 回答
-
p=1、9
\((q+4)^2=9\)
\((u+1)^2=45\)
- 回答
-
\(u=−1\pm3\sqrt{5}\)
\((z−5)^2=50\)
\((x−\frac{1}{4})^2=\frac{3}{16}\)
- 回答
-
\(x=\frac{1}{4}\pm\frac{\sqrt{3}}{4}\)
\((y−\frac{2}{3})^2=\frac{2}{9}\)
\((m−7)^2+6=30\)
- 回答
-
\(m=7\pm2\sqrt{6}\)
\((n−4)^2−50=150\)
\((5c+3)^2=−20\)
- 回答
-
没有解决办法
\((4c−1)^2=−18\)
\(m^2−6m+9=48\)
- 回答
-
\(m=3\pm4\sqrt{3}\)
\(n^2+10n+25=12\)
\(64a^2+48a+9=81\)
- 回答
-
a=−32、34
\(4b^2−28b+49=25\)
10.2 使用完成正方形求解二次方程
在以下练习中,完成正方形以形成完美的三项式方形。 然后将结果写成二项式平方。
\(x^2+22x\)
- 回答
-
\((x+11)^2\)
\(y^2+6y\)
\(m^2−8m\)
- 回答
-
\((m−4)^2\)
\(n^2−10n\)
\(a^2−3a\)
- 回答
-
\((a−\frac{3}{2})^2\)
\(b^2+13b\)
\(p^2+\frac{4}{5}p\)
- 回答
-
\((p+\frac{2}{5})^2\)
\(q^2−13q\)
在以下练习中,通过完成方块来求解。
\(c^2+20c=21\)
- 回答
-
c=1、−21
\(d^2+14d=−13\)
\(x^2−4x=32\)
- 回答
-
x=−4、8
\(y^2−16y=36\)
\(r^2+6r=−100\)
- 回答
-
没有解决办法
\(t^2−12t=−40\)
\(v^2−14v=−31\)
- 回答
-
\(v=7\pm3\sqrt{2}\)
\(w^2−20w=100\)
\(m^2+10m−4=−13\)
- 回答
-
\(m=−9,−1\)
\(n^2−6n+11=34\)
\(a^2=3a+8\)
- 回答
-
\(a=\frac{3}{2}\pm\frac{\sqrt{41}}{2}\)
\(b^2=11b−5\)
\((u+8)(u+4)=14\)
- 回答
-
\(u=−6\pm2\sqrt{2}\)
\((z−10)(z+2)=28\)
\(3p^2−18p+15=15\)
- 回答
-
p=0、6
\(5q^2+70q+20=0\)
\(4y^2−6y=4\)
- 回答
-
\(y=−\frac{1}{2}, 2\)
\(2x^2+2x=4\)
\(3c^2+2c=9\)
- 回答
-
\(c=−\frac{1}{3}\pm\frac{2\sqrt{7}}{3}\)
\(4d^2−2d=8\)
10.3 使用二次公式求解二次方程
在以下练习中,使用二次公式求解。
\(4x^2−5x+1=0\)
- 回答
-
\(x=14, 1\)
\(7y^2+4y−3=0\)
\(r^2−r−42=0\)
- 回答
-
\(r=−6, 7\)
\(t^2+13t+22=0\)
\(4v^2+v−5=0\)
- 回答
-
\(v=−\frac{5}{4}, 1\)
\(2w^2+9w+2=0\)
\(3m^2+8m+2=0\)
- 回答
-
\(m=\frac{−4\pm\sqrt{10}}{3}\)
\(5n^2+2n−1=0\)
\(6a^2−5a+2=0\)
- 回答
-
没有真正的解决方案
\(4b^2−b+8=0\)
\(u(u−10)+3=0\)
- 回答
-
\(u=5\pm2\sqrt{2}\)
\(5z(z−2)=3\)
\(\frac{1}{8}p^2−\frac{1}{5}p=−\frac{1}{20}\)
- 回答
-
\(p=\frac{4\pm\sqrt{6}}{5}\)
\(\frac{2}{5}q^2+\frac{3}{10}q=\frac{1}{10}\)
\(4c^2+4c+1=0\)
- 回答
-
\(c=−\frac{1}{2}\)
\(9d^2−12d=−4\)
在以下练习中,确定每个二次方程的解数。
- \(9x^2−6x+1=0\)
- \(3y^2−8y+1=0\)
- \(7m^2+12m+4=0\)
- \(5n^2−n+1=0\)
- 回答
-
- 1
- 2
- 2
- 无
- \(5x^2−7x−8=0\)
- \(7x^2−10x+5=0\)
- \(25x^2−90x+81=0\)
- \(15x^2−8x+4=0\)
在以下练习中,确定用于求解每个二次方程的最合适的方法(因子分解、平方根或二次公式)。
- \(16r^2−8r+1=0\)
- \(5t^2−8t+3=9\)\(3(c+2)^2=15\)
- 回答
-
- 因素
- 二次方程式
- 平方根
- \(4d^2+10d−5=21\)
- \(25x^2−60x+36=0\)
- \(6(5v−7)^2=150\)
10.4 求解由二次方程建模的应用程序
在以下练习中,使用分解方法、平方根原理或二次公式求解。
找出乘积为 323 的两个连续奇数。
- 回答
-
乘积为 323 的两个连续奇数分别为 17 和 19 以及 −17 和 −19。
找出乘积为 624 的两个连续偶数。
三角旗的面积为 351 平方厘米。 底座的长度比高度的四倍长两厘米。 找出底座的高度和长度。
- 回答
-
横幅的高度为 13 厘米,侧面的长度为 54 厘米。
朱利叶斯为他的硬币收藏制作了一个三角形陈列柜。 陈列柜的高度小于底座宽度的两倍六英寸。 手机壳背面的面积为 70 平方英寸。 找出表壳的高度和宽度。
直角三角形形状的瓷砖马赛克被用作矩形路径的拐角。 马赛克的斜边为 5 英尺。 马赛克的一面长度是另一面的两倍。 两边的长度是多少? 四舍五入到最接近的十分之一。

- 回答
-
马赛克边的长度分别为 2.2 英尺和 4.4 英尺。
一块矩形胶合板的对角线比宽度多两英尺。 胶合板的长度是宽度的两倍。 胶合板对角线的长度是多少? 四舍五入到最接近的十分之一。
从街道到帕姆家的前面步行道面积为250平方英尺。 它的长度比其宽度的四倍小两倍。 找出人行道的长度和宽度。 四舍五入到最接近的十分之一。
- 回答
-
前面步道的宽度为 8.1 英尺,长度为 30.8 英尺。
在索菲亚的毕业典礼上,将端到尾排列几张相同宽度的桌子,形成一张总面积为75平方英尺的餐桌。 表格的总长度将比宽度的三倍多两倍。 找到餐桌的长度和宽度,这样 Sophia 就可以购买正确尺寸的桌布。 将答案四舍五入到最接近的十分之一。
球垂直投向空中,速度为 160 英尺/秒。 使用公式\(h=−16t^2+v_{0}t\)来确定球何时会离地面 384 英尺。 四舍五入到最接近的十分之一。
- 回答
-
球将在 4 秒钟内向上移动 384 英尺,在向下的路上将在 6 秒钟内达到。
子弹以320英尺/秒的速度从地面直接向上发射。 使用该公式\(h=−16t^2+v_{0}t\)来确定子弹何时会达到 800 英尺。 四舍五入到最接近的十分之一。
10.5 在两个变量中绘制二次方程
在以下练习中,逐点绘图。
图表\(y=x^2−2\)
- 回答
-
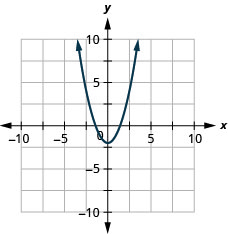
图表\(y=−x^2+3\)
在以下练习中,确定以下抛物线是向上还是向下打开。
\(y=−3x^2+3x−1\)
- 回答
-
向下
\(y=5x^2+6x+3\)
\(y=x^2+8x−1\)
- 回答
-
向上
A\(y=−4x^2−7x+1\)
在以下练习中,找到
- 对称轴和
- 顶点。
\(y=−x^2+6x+8\)
- 回答
-
- x=3
- (3,17)
\(y=2x^2−8x+1\)
在以下练习中,找到 x 和 y 截距。
\(y=x^2−4x+5\)
- 回答
-
y: (0,5); x: (5,0), (−1,0)
\(y=x^2−8x+15\)
\(y=x^2−4x+10\)
- 回答
-
y: (0,10);x: 无
\(y=−5x^2−30x−46\)
\(y=16x^2−8x+1\)
- 回答
-
y: (0,1);x: (14,0)
\(y=x^2+16x+64\)
在以下练习中,使用截距、顶点和对称轴绘制图形。
\(y=x^2+8x+15\)
- 回答
-
y: (0,15); x: (−3,0), (−5,0);
轴:x=−4;vertex :( −4, −1)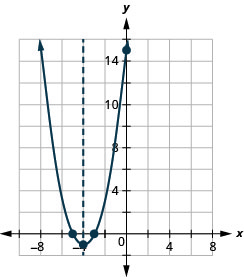
\(y=x^2−2x−3\)
\(y=−x^2+8x−16\)
- 回答
-
y: (0, −16); x: (4,0);
轴:x=4;顶点 :( 4,0)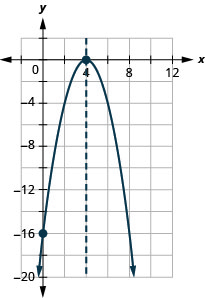
\(y=4x^2−4x+1\)
\(y=x^2+6x+13\)
- 回答
-
y: (0,13); x: none;
轴:x=−3; vertex :( −3,4)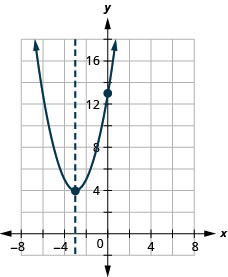
\(y=−2x^2−8x−12\)
\(y=−4x^2+16x−11\)
- 回答
-
y: (0, −11); x: (3.1,0), (0.9,0);
轴:x=2;顶点 :( 2,5)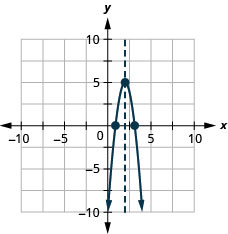
\(y=x^2+8x+10\)
在以下练习中,找到最小值或最大值。
\(y=7x^2+14x+6\)
- 回答
-
当时,最小值为 −1\(x=−1\)。
\(y=−3x^2+12x−10\)
在以下练习中,求解。 将答案四舍五入到最接近的十分之一。
球从地面向上投掷,初始速度为 112 英尺/秒。 使用二次方程计算\(h=−16t^2+112t\)球达到最大高度需要多长时间,然后找到最大高度。
- 回答
-
在 3.5 秒内,球将达到 196 英尺的最大高度。
日托设施在建筑物侧面封闭了一个矩形区域,供孩子们在户外玩耍。 他们需要在院子的三边使用 180 英尺的围栏来最大限度地扩大面积。 二次方程\(A=−2x^2+180x\)给出了码的面积 A,表示与院子接壤的建筑物的长度 x。 找到应与院子接壤的建筑物的长度以最大化面积,然后找到最大面积。
练习测试
使用平方根属性求解二次方程:\(3(w+5)^2=27\).
- 回答
-
w=−2、−8
使用完成方程来求解二次方程:\(a^2−8a+7=23\)
使用二次公式求解二次方程:\(2m^2−5m+3=0\).
- 回答
-
m=1、32
求解以下二次方程。 使用任何方法。
\(8v^2+3=35\)
\(3n^2+8n+3=0\)
- 回答
-
\(n=\frac{−4\pm\sqrt{7}}{3}\)
\(2b^2+6b−8=0\)
\(x(x+3)+12=0\)
- 回答
-
没有真正的解决方案
\(\frac{4}{3}y^2−4y+3=0\)
使用判别来确定每个二次方程的解数。
\(6p^2−13p+7=0\)
- 回答
-
2
\(3q^2−10q+12=0\)
通过因式分解、平方根属性或二次公式求解。
找出乘积为 360 的两个连续偶数。
- 回答
-
两个连续的偶数是 −20 和 −18 以及 18 和 20。
矩形对角线的长度比宽度多三倍。 矩形的长度是宽度的三倍。 找出对角线的长度。 (四舍五入到最接近的十分之一。)
对于每个抛物线,找到
- 它以哪种方式打开,
- 对称轴,
- 顶点,
- x-和 y-截取,以及
- 最大值或最小值。
\(y=3x^2+6x+8\)
- 回答
-
- 向上
- \(x=−1\)
- (−1,5)
- y: (0,8);x: 无;y: (0,8)
- 最小值为 5 时\(x=−1\)。
\(y=x^2−4\)
\(y=x^2+10x+24\)
- 回答
-
- 向上
- \(x=−5\)
- (−5、−1)
- y: (0,24); x: (−6,0), (−4,0)
- 最小值为 −5 时\(x=−1\)
\(y=−3x^2+12x−8\)
\(y=−x^2−8x+16\)
- 回答
-
- 向下
- \(x=−4\)
- (−4,32)
- y; (0,16); x: (−9.7,0), (1.7,0)
- 最大值为 32 时\(x=−4\)
使用截距、顶点和对称轴绘制以下抛物线图。
\(y=2x^2+6x+2\)
\(y=16x^2+24x+9\)
- 回答
-
y: (0,9); x: (−34,0)
轴:\( x=−\frac{3}{4}\); 顶点:\((−\frac{3}{4},0)\)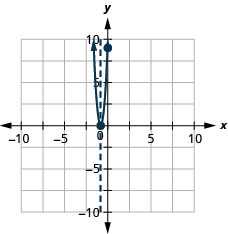
解决。
水气球以 86 英尺/秒的速度向上发射。 使用公式 h=−16t^2+86t,找出气球达到最大高度需要多长时间,然后找到最大高度。 四舍五入到最接近的十分之一。