10.4:求解由二次方程建模的应用程序
- Page ID
- 204466
在本节结束时,您将能够:
- 求解由二次方程建模的应用程序
求解二次公式的应用
我们之前求解了一些由二次方程建模的应用程序,当时我们唯一的求解方法是分解。 现在我们有了更多的求解二次方程的方法,我们再来看一下应用。 为了让我们开始,我们将在这里复制我们通常的问题解决策略,以便我们可以按照步骤操作。
- 阅读问题。 确保所有文字和想法都被理解。
- 确定我们在寻找什么。
- 说出我们要找的东西。 选择一个变量来表示该数量。
- 翻译成方程式。 用一句话用所有重要信息重述问题可能会有所帮助。 然后,将英语句子翻译成代数方程。
- 使用良好的代数技巧求@@ 解方程。
- 检查问题中的答案并确保答案合理。
- 用完整的句子@@ 回答问题。
通过使用线性方程对情况进行建模,我们已经求解了涉及连续偶数整数和连续奇数整数的数字应用程序。 请记住,我们注意到每个偶数都比其前面的数字多 2。 如果我们把第一个叫做 n,那么下一个是\(n+2\). The next one would be \(n+2+2\) or \(n+4\). This is also true when we use odd integers. One set of even integers and one set of odd integers are shown below.
\[\begin{array}{cccc} {}&{\textbf{Consecutive even integers}}&{}&{\textbf{Consecutive odd integers}}\\ {}&{64, 66, 68}&{}&{77, 79, 81}\\ {n}&{1^{st} \text{even number}}&{n}&{1^{st} \text{odd number}}\\ {n+2}&{2^{nd} \text{even number}} &{n+2}&{2^{nd} \text{odd number}}\\ {n+4}&{3^{rd} \text{even number}}&{n+4}&{3^{rd} \text{odd number}}\\ \end{array}\]
连续奇数整数或连续偶数整数的某些应用是通过二次方程建模的。 上面的表示法在你命名变量时会有所帮助。
两个连续奇数整数的乘积为 195。 找到整数。
- 回答
-
第 1 步。 阅读问题。 第 2 步。 确定我们在寻找什么。 我们正在寻找两个连续的奇数整数。 第 3 步。 说出我们要找的东西。 假设\(n=\)第一个奇数整数。
\(n+2=\)下一个奇数整数第 4 步。 翻译成方程式。 用一句话陈述问题。 “两个连续奇数整数的乘积为 195。” 第一个奇数整数和第二个奇数整数的乘积为 195。 翻译成方程式。 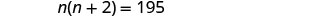
第 5 步。 求解方程。 分发。 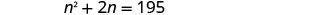
减去 195 得出标准形式的方程式。 
确定 a、b、c 的值。 
写下二次方程。 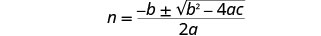
然后用 a、b、c 的值代替。 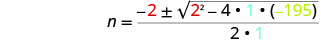
简化。 
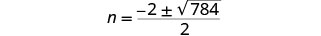
简化激进。 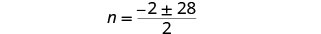
重写以显示两个解决方案。 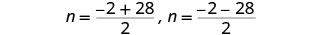
求解每个方程。 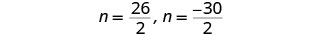
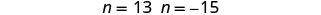
n 有两个值是解。 这将为我们的解提供两对连续的奇数整数。 第一个奇数整数 n=13
下一个奇数整数 n+2
13+2
15第一个奇数整数 n=−15
下一个奇数整数 n+2
−15+2
−13第 6 步。 检查答案。
这些对能起作用吗?
它们是连续的奇数整数吗?
他们的产品是 195 吗?13、15、是的 −13、−15、是的
13⋅15=195,是的 −13 (−15) =195,是的
第 7 步。 回答问题。 乘积为 195 的两个连续奇数整数分别为 13、15 和 −13、−15。
两个连续奇数整数的乘积为 99。 找到整数。
- 回答
-
乘积为 99 的两个连续奇数分别为 9 和 11 以及 −9 和 −11。
两个连续奇数整数的乘积为 168。 找到整数。
- 回答
-
乘积为 168 的两个连续偶数分别为 12 和 14 以及 −12 和 −14。
我们将使用三角形面积的公式来求解下一个示例。
对于以 b 为基数且高度为 h 的三角形,面积 A 由公式给出\(A=\frac{1}{2}bh\)。
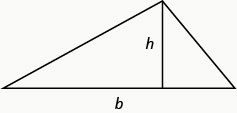
回想一下,当我们求解几何应用程序时,绘制图形会很有帮助。
一位建筑师正在设计一家餐厅的入口通道。 她想在门口上方放一扇三角窗。 由于能源限制,窗户的面积可以为 120 平方英尺,建筑师希望宽度为 4 英尺,而不是高度的两倍。 找出窗口的高度和宽度。
- 回答
-
第 1 步。 阅读问题。
画一张照片。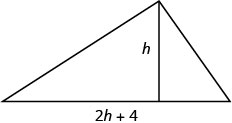
第 2 步。 确定我们在寻找什么。 我们正在寻找高度和宽度。 第 3 步。 说出我们要找的东西。 假\(h=\)设三角形的高度。
\(2h+4=\)三角形的宽度第 4 步。 翻译。 我们知道这个地区。 写出三角形面积的公式。

第 5 步。 求解方程。 在值中替换。 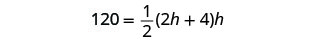
分发。 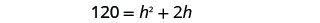
这是一个二次方程,用标准形式重写。 
使用二次公式求解方程。 确定 a、b、 c 的值。 
写下二次方程。 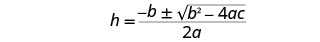
然后用 a、b、c 的值代替。 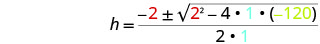
简化。 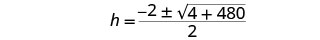
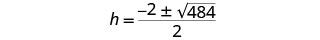
简化激进。 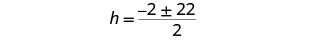
重写以显示两个解决方案。 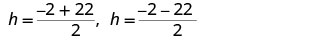
简化。 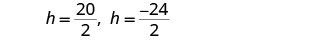
由于 h 是窗口的高度,因此值\(h=−12\)没有意义。 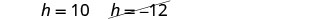
三角形的高度:三角形\(h=10\)
的宽度:\(2h+4\)
\(2⋅10+4\)
\(24\)第 6 步。 检查答案。 高度为 10、宽度为 24 的三角形的面积是否为 120? 是的。 第 7 步。 回答问题。 三角窗的高度为 10 英尺,宽度为 24 英尺。 请注意,解是整数。 这告诉我们,我们可以通过分解来求解方程。
当我们用标准形式编写方程时\(h^2+2h−120=0\),我们本可以将其考虑在内。 如果我们这样做了,我们就会解出这个方程式\((h+12)(h−10)=0\)。
找出一个三角形的尺寸,该三角形的宽度是其高度的四倍以上,面积为 208 平方英寸。
- 回答
-
三角形的高度为 8 英寸,宽度为 52 英寸。
如果面积为 110 平方英尺的三角形的高度小于两倍宽度的两倍,那么它的尺寸是多少?
- 回答
-
三角形的高度为 20 英尺,宽度为 11 英尺。
在前两个示例中,二次公式中激进部分中的数字是一个完美的正方形,因此解是有理数。 如果我们得到一个非理性数作为应用程序问题的解,我们将使用计算器来得到一个近似值。
毕达哥拉斯定理给出了直角三角形的腿和斜边之间的关系。 我们将使用毕达哥拉斯定理来求解下一个例子。
在任何直角三角形中,a 和 b 是腿的长度,c 是斜边的长度,\(a^2+b^2=c^2\)
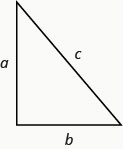
Rene 正在设置节日灯光显示屏。 他想做一棵两个直角三角形的 “树”,如下所示,两侧有两根 10 英尺长的灯串可供使用。 他会把灯固定在杆子的顶部和地上的两个木桩上。 他希望杆子的高度与杆底到每个木桩的距离相同。 杆子应该有多高?
- 回答
-
第 1 步。 阅读问题。 画一张照片 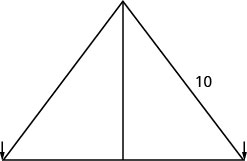
第 2 步。 确定我们在寻找什么。 我们正在寻找杆子的高度。 第 3 步。 说出我们要找的东西。 从杆子底部到任一木桩的距离与杆子的高度相同。 假\(x=\)设杆子的高度。
\(x=\)从杆子到木桩的距离每边都是一个直角三角形。 我们画了其中一张照片。 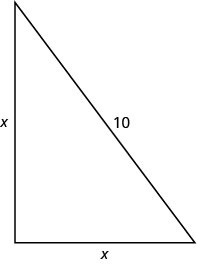
第 4 步。 翻译成方程式。 我们可以使用毕达哥拉斯定理来求解 x。 写下毕达哥拉斯定理。 \(a^2+b^2=c^2\) 第 5 步。 求解方程。 替代。 \(x^2+x^2=10^2\) 简化。 \(2x^2=100\) 除以 2 分离出变量。 \(\frac{2x^2}{2}=\frac{100}{2}\) 简化。 \(x^2=50\) 使用平方根属性。 \(x=\pm\sqrt{50}\) 简化激进。 \(x=\pm5\sqrt{2}\) 重写以显示两个解决方案。 \(x=5\sqrt{2}\)
\(\not{x=−5\sqrt{2}}\)用计算器将这个数字近似到最接近的十分之一。 \(x \approx 7.1\) 第 6 步。 检查答案。
在毕达哥拉斯定理中自己检查一下。第 7 步。 回答问题。 杆子应高约 7.1 英尺。
太阳从旗杆上投下阴影。 旗杆的高度是其阴影长度的三倍。 阴影末端与旗杆顶部之间的距离为 20 英尺。 找出阴影的长度和旗杆的长度。 四舍五入到最接近的十分之一英尺。
- 回答
-
阴影的长度为 6.3 英尺,旗杆的长度为 18.9 英尺。
矩形场的对角之间的距离比该场的宽度多四个。 字段的长度是其宽度的两倍。 找出相反角落之间的距离。 四舍五入到最接近的十分之一。
- 回答
-
到对面角落的距离为 3.2。
迈克想在他的前院放一块 150 平方英尺的人造草皮。 这是他的房主协会允许的最大人造草坪面积。 他想要一个长度小于三倍宽度一英尺的长方形草皮区域。 找到长度和宽度。 四舍五入到最接近的十分之一英尺。
- 回答
-
第 1 步。 阅读问题。 画一张照片。 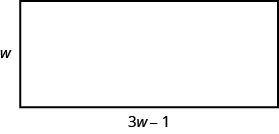
第 2 步。 确定我们在寻找什么。 我们正在寻找长度和宽度。 第 3 步。 说出我们要找的东西。 假\(w=\)设矩形的宽度。
\(3w−1=\)矩形的长度第 4 步。 翻译成方程式。
我们知道这个地区。 写出矩形面积的公式。
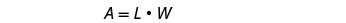
第 5 步。 求解方程。 在值中替换。 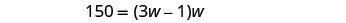
分发。 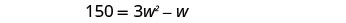
这是一个二次方程,用标准形式重写。 
使用二次公式求解方程。 确定 a、b、c 的值。 
写下二次方程式。 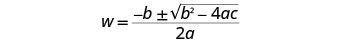
然后用 a、b、c 的值代替。 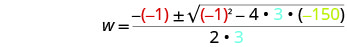
简化。 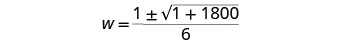
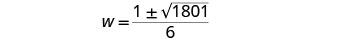
重写以显示两个解决方案。 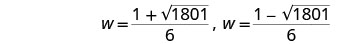
使用计算器估算答案。
我们消除了宽度的负解。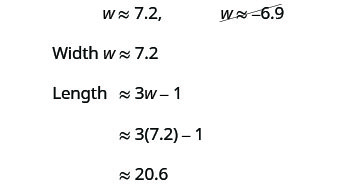
第 6 步。 检查答案。
确保答案有意义。第 7 步。 回答问题。 矩形的宽度约为 7.2 英尺,长度为 20.6 英尺。
200 平方英尺的矩形菜园的长度比宽度的两倍小四英尺。 找出花园的长度和宽度。 四舍五入到最接近的十分之一英尺...
- 回答
-
花园的宽度为 11 英尺,长度为 18 英尺。
矩形桌布的面积为 80 平方英尺。 宽度比长度短 5 英尺。 桌布的长度和宽度是多少? 四舍五入到最接近的十分之一英尺。
- 回答
-
桌布的宽度为 6.8 英尺,长度为 11.8 英尺。
向上射弹的高度由二次方程建模。 初始速度推动物体向上推动,\(v_{0}\)直到重力导致物体向下回落。
t 秒后以初始速度向上射入空中的物体的高度(以英尺 h 为单位)由公式给出:\(v_{0}\)
\(h=−16t^2+v_{0}t\)
我们可以使用弹丸运动的公式来计算烟花达到特定高度需要多少秒。
烟花以每秒 130 英尺的初始速度向上射击。 达到 260 英尺的高度需要几秒钟? 四舍五入到最接近的十分之一秒。
- 回答
-
第 1 步。 阅读问题。 第 2 步。 确定我们在寻找什么。 我们正在寻找秒数,也就是时间。 第 3 步。 说出我们要找的东西。 假\(t=\)设秒数。 第 4 步。 翻译成方程式。 使用公式。 \(h=−16t^2+v_{0}t\) 第 5 步。 求解方程。
我们知道速度\(v_{0}\)是每秒 130 英尺。高度为 260 英尺。 替换这些值。 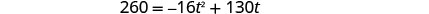
这是一个二次方程,用标准形式重写。 
使用二次公式求解方程。 确定 a、b、c 的值。 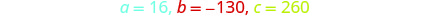
写下二次方程式。 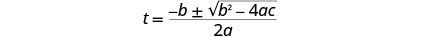
然后用 a、b、c 的值代替。 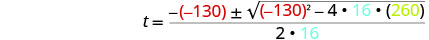
简化。 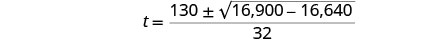
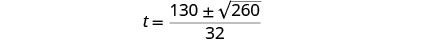
重写以显示两个解决方案。 
用计算器估算答案。 \(t \approx 4.6\)秒,\(t \approx 3.6\) 第 6 步。 检查答案。
支票留给你了。第 7 步。 回答问题。 烟花会上升然后掉下来。
随着烟花上升,
大约 3.6 秒后烟花将达到 260 英尺。 它还将在向下的路上
以 4.6 秒的速度超过这个高度。

一支箭从地面射向空中,初始速度为 108 英尺/秒。 使用公式\(h=−16t^2+v_{0}t\)确定箭头何时离地面 180 英尺。 四舍五入最接近的十分之一秒。
- 回答
-
箭在向上的路上将在 3 秒钟内达到 180,向下的路上将在 3.8 秒后达到 180。
一个人以 96 英尺/秒的速度向空中投球。 使用公式\(h=−16t^2+v_{0}t\)确定何时球的高度将为 48 英尺。 四舍五入到最接近的十分之一秒。
- 回答
-
球将在 0.6 秒内向上移动 48 英尺,在 5.5 秒后向下移动。
访问这些在线资源,获取更多指导和练习使用二次方程解决单词问题:
关键概念
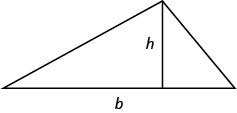
- 三角形的面积对于基数为 b、高度为 h 的三角形,面积 A 由以下公式给出:\(A=\frac{1}{2}bh\)
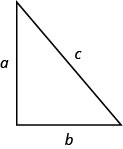
- 毕达哥拉斯定理在任何直角三角形中,其中 a 和 b 是腿的长度,c 是假设的长度,\(a^2+b^2=c^2\)
- 射弹运动在 tt 秒之后,可以用公式建模以初始速度向上射向空中的物体的高度(以英尺 h 为单位)\(v_{0}\)
\(h=−16t^2+v_{0}t\)
词汇表
- 连续的偶数整数
- 连续的偶数整数是紧随其后的偶数整数。 如果一个偶数由 n 表示,则下一个连续的偶数是\(n+2\),后面的下一个偶数是\(n+4\)。
- 连续的奇数整数
- 连续的奇数整数是紧随其后的奇数整数。 如果奇数整数由 n 表示,则下一个连续的奇数整数是\(n+2\),后面的下一个奇数是\(n+4\)。


