10.3E:练习
- Page ID
- 204518
练习成就完美
使用二次公式求解二次方程
在以下练习中,使用二次公式求解。
\(4m^2+m−3=0\)
- 回答
-
\(m=−1\),\(m=\frac{3}{4}\)
\(4n^2−9n+5=0\)
\(2p^2−7p+3=0\)
- 回答
-
\(p=\frac{1}{2}\),\(p=3\)
\(3q^2+8q−3=0\)
\(p^2+7p+12=0\)
- 回答
-
\(p=−4\),\(p=−3\)
\(q^2+3q−18=0\)
\(r^2−8r−33=0\)
- 回答
-
\(r=−3\),\(r=11\)
\(t^2+13t+40=0\)
\(3u^2+7u−2=0\)
- 回答
-
\(u=\frac{−7\pm\sqrt{73}}{6}\)
\(6z^2−9z+1=0\)
\(2a^2−6a+3=0\)
- 回答
-
\(a=\frac{3\pm\sqrt{3}}{2}\)
\(5b^2+2b−4=0\)
\(2x^2+3x+9=0\)
- 回答
-
没有真正的解决方案
\(6y^2−5y+2=0\)
\(v(v+5)−10=0\)
- 回答
-
\(v=\frac{−5\pm\sqrt{65}}{2}\)
\(3w(w−2)−8=0\)
\(\frac{1}{3}m^2+\frac{1}{12}m=\frac{1}{4}\)
- 回答
-
\(m=−1\),\(m=\frac{3}{4}\)
\(\frac{1}{3}n^2+n=−\frac{1}{2}\)
\(16c^2+24c+9=0\)
- 回答
-
\(c=−\frac{3}{4}\)
\(25d^2−60d+36=0\)
5m^2+2m−7=0
- 回答
-
\(m=−\frac{7}{5}\),\(m=1\)
\(8n^2−3n+3=0\)
\(p^2−6p−27=0\)
- 回答
-
\(p=−3\),\(p=9\)
\(25q^2+30q+9=0\)
\(4r^2+3r−5=0\)
- 回答
-
\(r=\frac{−3\pm\sqrt{89}}{8}\)
\(3t(t−2)=2\)
\(2a^2+12a+5=0\)
- 回答
-
\(a=\frac{−6\pm\sqrt{26}}{2}\)
\(4d^2−7d+2=0\)
\(\frac{3}{4}b^2+\frac{1}{2}b=\frac{3}{8}\)
- 回答
-
\(b=\frac{−2\pm\sqrt{11}}{6}\)
\(\frac{1}{9}c^2+\frac{2}{3}c=3\)
\(2x^2+12x−3=0\)
- 回答
-
\(x=\frac{−6\pm\sqrt{42}}{4}\)
\(16y^2+8y+1=0\)
使用判别法预测二次方程的解数
在以下练习中,确定每个二次方程的解数。
- \(4x^2−5x+16=0\)
- \(36y^2+36y+9=0\)
- \(6m^2+3m−5=0\)
- \(18n^2−7n+3=0\)
- 回答
-
- 没有真正的解决方案
- 1
- 2
- 没有真正的解决方案
- \(9v^2−15v+25=0\)
- \(100w^2+60w+9=0\)
- \(5c^2+7c−10=0\)
- \(15d^2−4d+8=0\)
- \(r^2+12r+36=0\)
- \(8t^2−11t+5=0\)
- \(4u^2−12u+9=0\)
- \(3v^2−5v−1=0\)
- 回答
-
- 1
- 没有真正的解决方案
- 1
- 2
- \(25p^2+10p+1=0\)
- \(7q^2−3q−6=0\)
- \(7y^2+2y+8=0\)
- \(25z^2−60z+36=0\)
确定用于求解二次方程的最合适方法
在以下练习中,确定用于求解每个二次方程的最合适的方法(因子分解、平方根或二次公式)。 不要解决。
- \(x^2−5x−24=0\)
- \((y+5)^2=12\)
- \(14m^2+3m=11\)
- 回答
-
- 因素
- 平方根
- 二次公式
- \((8v+3)^2=81\)
- \(w^2−9w−22=0\)
- \(4n^2−10=6\)
- \(6a^2+14=20\)
- \((x−\frac{1}{4})^2=\frac{5}{16}\)
- \(y^2−2y=8\)
- 回答
-
- 因素
- 平方根
- 因素
- \(8b^2+15b=4\)
- \(\frac{5}{9}v^2−\frac{2}{3}v=1\)
- \((w+\frac{4}{3})^2=\frac{2}{9}\)
日常数学
一枚照明弹是从海上船上直接向上发射的。 求解 t 的方程\(16(t^2−13t+40)=0\),即耀斑在 640 英尺的高度所需的秒数。
- 回答
-
5 秒 8 秒
一位建筑师正在设计酒店大堂。 她想要一扇三角形的窗户望向中庭,窗户的宽度比高度多6英尺。 由于能源限制,窗户的面积必须为 140 平方英尺。 求解 h 的方程\(\frac{1}{2}h^2+3h=140\),即窗口的高度。
写作练习
求解方程\(x^2+10x=200\)
- 通过完成正方形
- 使用二次公式
- 你更喜欢哪种方法? 为什么?
- 回答
-
- −20、10
- −20、10
- 答案会有所不同
求解方程\(12y^2+23y=24\)
- 通过完成正方形
- 使用二次公式
- 你更喜欢哪种方法? 为什么?
自检
ⓐ 完成练习后,使用这份清单来评估你对本节目标的掌握程度。
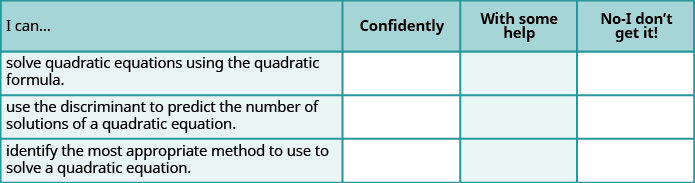
ⓑ 这份清单告诉你你对本部分的掌握情况了什么? 你会采取哪些措施来改进?


