10.3:使用二次公式求解二次方程
- Page ID
- 204499
在本节结束时,您将能够:
- 使用二次公式求解二次方程
- 使用判别函数预测二次方程的解数
- 确定用于求解二次方程的最合适方法
当我们在最后一节中通过完成正方形求解二次方程时,我们每次都采取相同的步骤。 在练习集结束时,你可能想知道 “没有更简单的方法可以做到这一点吗?” 答案是 “是”。 在本节中,我们将推导并使用公式来找到二次方程的解。
我们已经看到了如何 “一般地” 求解特定变量的公式,这样我们就可以只做一次代数步骤,然后使用新公式来找出特定变量的值。 现在,我们将通过完成一般正方形的步骤来求解 x 的二次方程。 看一下最后一节结尾处的其中一个例子可能会有所帮助,当你通读下面的代数步骤时,我们在这个例子中求解了一个形式\( ax^2+bx+c=0\)的方程,这样你就可以看到它们是用数字和 “一般的” 来看的。
| 我们从二次方程的标准形式开始,然后通过完成方程来求解 x。 | \( ax^2+bx+c=0\) | |
| 隔离一侧的变量项。 | \( ax^2+bx=−c\) | |
| 将前导系数 1 除以 a。 | \(\frac{ax^2}{a}+\frac{b}{a}x=−\frac{c}{a}\) | |
| 简化。 | \(x^2+\frac{b}{a}x=−\frac{c}{a}\) | |
|
要完成正方形,请找到\((\frac{1}{2}·\frac{b}{a})^2\)并将其添加到方程的两边。 \((\frac{1}{2}\frac{b}{a})^2=\frac{b^2}{4a^2}\) |
\(x^2+\frac{b}{a}x+\frac{b^2}{4a^2}=−\frac{c}{a}+\frac{b^2}{4a^2}\) | |
| 左边是一个完美的正方形,将其考虑在内。 | \((x+\frac{b}{2a})^2=−\frac{c}{a}+\frac{b^2}{4a^2}\) | |
| 找到右侧的公分母,用公分母写出等效分数。 | \((x+\frac{b}{2a})^2=−\frac{c·4a}{a·4a}+\frac{b^2}{4a^2}\) | |
| 简化。 | \((x+\frac{b}{2a})^2=\frac{b^2}{4a^2}−\frac{4ac}{4a^2}\) | |
| 合并为一个分数。 | \((x+\frac{b}{2a})^2=\frac{b^2−4ac}{4a^2}\) | |
| 使用平方根属性。 | \((x+\frac{b}{2a})=\pm\sqrt{\frac{b^2−4ac}{4a^2}}\) | |
| 简化。 | \((x+\frac{b}{2a})=\pm\frac{\sqrt{b^2−4ac}}{2a}\) | |
| 加\(−\frac{b}{2a} \)到等式的两边。 | \(x=−\frac{b}{2a}\pm\frac{\sqrt{b^2−4ac}}{2a}\) | |
| 合并右侧的术语。 | \(x=\frac{−b\pm\sqrt{b^2−4ac}}{2a}\) | |
最后一个方程是二次公式。
这种形式的\(ax^2+bx+c=0\)二次方程的解由以下公式给出:\(a\ge 0\)
\(x=\frac{−b\pm\sqrt{b^2−4ac}}{2a}\)
要使用二次公式,我们将 a、b 和 c 的值替换为公式右侧的表达式。 然后,我们进行所有数学运算以简化表达式。 结果给出了二次方程的解。
使用二次公式求解\(2x^2+9x−5=0\)。
- 回答
-


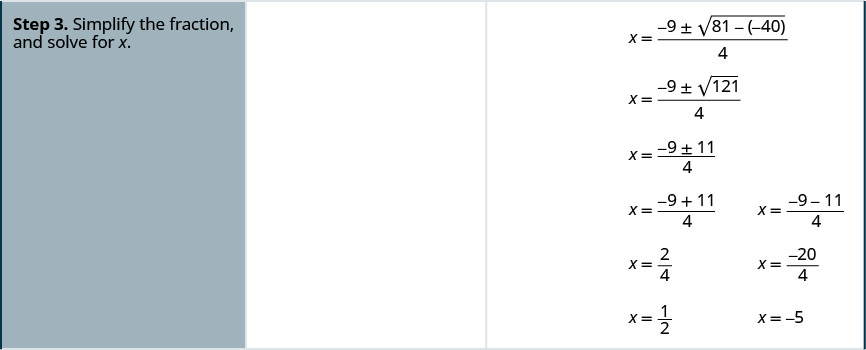

使用二次公式求解\(3y^2−5y+2=0\)。
- 回答
-
\(y=\frac{2}{3}\),\(y=1\)
使用二次公式求解\(4z^2+2z−6=0\)。
- 回答
-
\(z=−\frac{3}{2}\),\(z=1\)
- 用标准形式写下二次公式。 识别 aa、bb 和 cc 的值。
- 写下二次方程式。 然后用 a、b 和 c 的值进行替换。
- 简化。
- 检查解决方案。
如果你在写每个问题时说出这个公式,你很快就会记住它。 请记住,二次公式是一个方程。 请务必以 “\(x=\)” 开头。
使用二次公式求解\(x^2−6x+5=0\)。
- 回答
-

这个方程是标准形式。 
确定 a、b、c 的值。 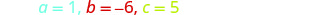
写下二次方程式。 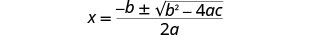
然后用 a、b、c 的值代替。 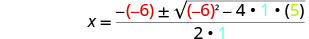
简化。 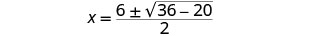
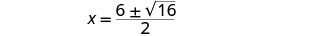
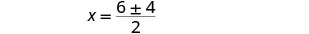
重写以显示两个解决方案。 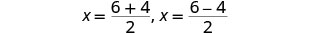
简化。 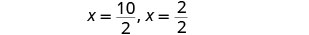
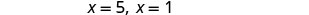
查看。
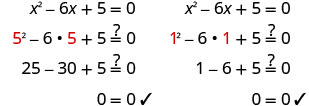
使用二次公式求解\(a^2−2a−15=0\)。
- 回答
-
\(a=−3\),\(a=5\)
使用二次公式求解\(b^2+10b+24=0\)。
- 回答
-
\(b=−6\),\(b=−4\)
当我们使用平方根属性求解二次方程时,我们有时会得到含有激进的答案。 使用二次方程式时也可能发生这种情况。 如果我们以激进作为解决方案,则最终答案必须采用简化形式的激进分子。
使用二次公式求解\(4y^2−5y−3=0\)。
- 回答
-
我们可以使用二次公式求解二次方程中的变量,无论它是否被命名为 “x”。

这个方程是标准形式。 
确定 a、b、c 的值。 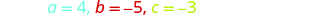
写下二次方程式。 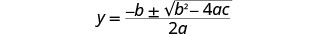
然后用 a、b、c 的值代替。 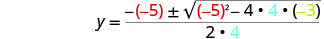
简化。 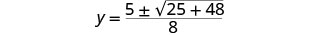
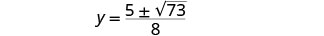
重写以显示两个解决方案。 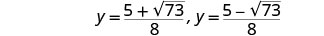
查看。 我们把支票留给你。
使用二次公式求解\(2p^2+8p+5=0\)。
- 回答
-
\(p=\frac{−4\pm\sqrt{6}}{2}\)
使用二次公式求解\(5q^2−11q+3=0\)。
- 回答
-
\(q=\frac{11\pm\sqrt{61}}{10}\)
使用二次公式求解\(2x^2+10x+11=0\)。
- 回答
-

这个方程是标准形式。 
确定 a、b、c 的值。 
写下二次方程式。 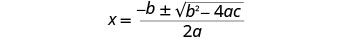
然后用 a、b、c 的值代替。 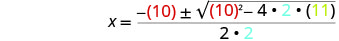
简化。 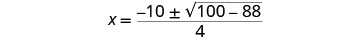
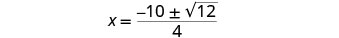
简化激进。 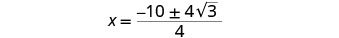
分解出分子中的公因子。 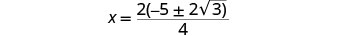
移除常见因素。 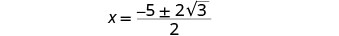
重写以显示两个解决方案。 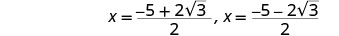
查看。 我们把支票留给你。
使用二次公式求解\(3m^2+12m+7=0\)。
- 回答
-
\(m=\frac{−6\pm\sqrt{15}}{3}\)
使用二次公式求解\(5n^2+4n−4=0\)。
- 回答
-
\(n=\frac{−2\pm2\sqrt{6}}{5}\)
我们不能取负数的平方根。 因此,当我们在二次公式中替换 a、b 和 c 时,如果自由基内部的量为负,则二次方程没有实际解。 我们将在下一个示例中看到这一点。
使用二次公式求解\(3p^2+2p+9=0\)。
- 回答
-
这个方程是标准形式。 
确定 a、b、c 的值。 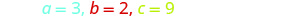
写下二次方程式。 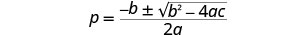
然后用 a、b、c 的值代替。 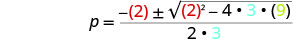
简化。 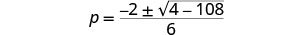
简化激进。 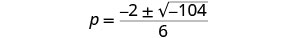
我们不能取负数的平方根。 没有真正的解决方案。
使用二次公式求解\(4a^2−3a+8=0\)。
- 回答
-
没有真正的解决方案
使用二次公式求解\(5b^2+2b+4=0\)。
- 回答
-
没有真正的解决方案
到目前为止,我们在本节中求解的二次方程都是以标准形式编写的\(ax^2+bx+c=0\)。 有时,我们需要先做一些代数才能使方程变为标准形式,然后才能使用二次公式。
使用二次公式求解\(x(x+6)+4=0\)。
- 回答
-

分布以获得标准形式的方程。 
这个方程现在是标准形式。 
确定 a、b、c 的值。 
写下二次方程式。 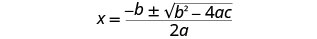
然后用 a、b、c 的值代替。 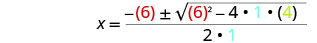
简化。 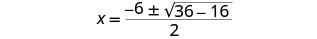
在激进内部进行简化。 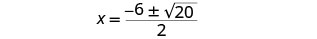
简化激进。 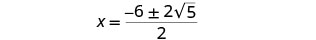
分解出分子中的公因子。 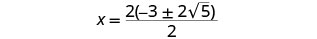
移除常见因素。 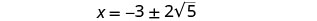
重写以显示两个解决方案。 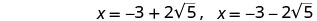
查看。 我们把支票留给你。
使用二次公式求解\(x(x+2)−5=0\)。
- 回答
-
\(x=−1\pm\sqrt{6}\)
使用二次公式求解\(y(3y−1)−2=0\)。
- 回答
-
\(y=−\frac{2}{3}\),\(y=1\)
当我们求解线性方程时,如果一个方程有太多的分数,我们会通过将方程的两边乘以液晶显示屏来 “清除分数”。 这给了我们一个等效方程——没有分数——需要求解。 我们可以对二次方程使用相同的策略。
使用二次公式求解\(\frac{1}{2}u^2+\frac{2}{3}u=\frac{1}{3}\)。
- 回答
-
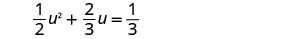
将两边乘以液晶屏 6 以清除分数。 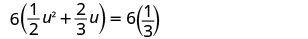
乘。 
减去 2 得到标准形式的方程。 
确定 a、b、c 的值。 
写下二次方程式。 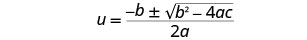
然后用 a、b、c 的值代替。 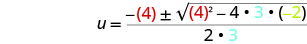
简化。 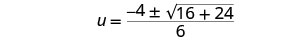
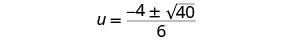
简化激进。 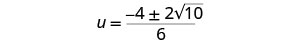
分解出分子中的公因子。 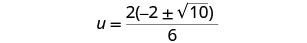
移除常见因素。 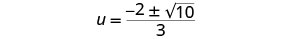
重写以显示两个解决方案。 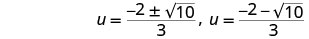
查看。 我们把支票留给你。
使用二次公式求解\(\frac{1}{4}c^2−\frac{1}{3}c=\frac{1}{12}\)。
- 回答
-
\(c=\frac{2\pm\sqrt{7}}{3}\)
使用二次公式求解\(\frac{1}{9}d^2−\frac{1}{2}d=−\frac{1}{2}\)。
- 回答
-
\(d=\frac{3}{2}\),\(d=3\)
想想这个方程式\((x−3)^2=0\). We know from the Zero Products Principle that this equation has only one solution: \(x=3\).
在下一个示例中,我们将看到使用二次公式求解具有完美正方形的方程如何也只能得出一个解。
使用二次公式求解\(4x^2−20x=−25\)。
- 回答
-

加 25 得出标准形式的方程。 
确定 a、b、c 的值。 
写下二次方程式。 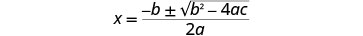
然后用 a、b、c 的值代替。 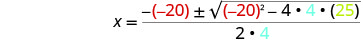
简化。 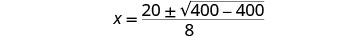
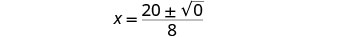
简化激进。 
简化分数。 
查看。 我们把支票留给你。 你认出那\(4x^2−20x+25\)是一个完美的正方形吗?
使用二次公式求解\(r^2+10r+25=0\)。
- 回答
-
\(r=−5\)
使用二次公式求解\(25t^2−40t=−16\)。
- 回答
-
\(t=\frac{4}{5}\)
使用判别法预测二次方程的解数
当我们在前面的例子中求解二次方程时,有时候我们会得到两个解,有时是一个解,有时没有真正的解。 有没有办法在不实际求解方程的情况下预测二次方程的解数?
是的,二次公式的基数内部的量使我们很容易确定解的数量。 这个量被称为判别量。
在二次公式中\(x=\frac{−b\pm\sqrt{b^2−4ac}}{2a}\),量被\(b^2−4ac\)称为判别值。
让我们来看看 “示例” 、 “示例” 和 “示例” 中方程的判别值,以及这些二次方程的解数。
| 二次方程(标准形式) | 判别性\(b^2−4ac\) | 判别者的标志 | 实际解的数量 | |
|---|---|---|---|---|
| 示例 | \(2x^2+9x−5=0\) | \ (b^2−4ac\)” data-valign= “middle” class= “lt-math-15194” >\(9^2−4·2(−5)=121\) | + | 2 |
| 示例 | \(4x^2−20x+25=0\) | \ (b^2−4ac\)” data-valign= “middle” class= “lt-math-15194” >\((−20)^2−4·4·25=0\) | 0 | 1 |
| 示例 | \(3p^2+2p+9=0\) | \ (b^2−4ac\)” data-valign= “middle” class= “lt-math-15194” >\(2^2−4·3·9=−104\) | − | 0 |
当判别值为正时\(x=\frac{−b\pm\sqrt{+}}{2a}\),二次方程有两个解。
当判别值为零\(x=\frac{−b\pm\sqrt{0}}{2a}\)时,二次方程有一个解。
当判别值为负\(x=\frac{−b\pm\sqrt{−}}{2a}\)时,二次方程没有实际解。
对于形式的二次方程\(ax^2+bx+c=0\)\(a \ge 0\),
- if\(b^2−4ac>0\),该方程有两个解。
- if\(b^2−4ac=0\),方程只有一个解。
- if\(b^2−4ac<0\),方程没有实际解。
确定每个二次方程的解数:
- \(2v^2−3v+6=0\)
- \(3x^2+7x−9=0\)
- \(5n^2+n+4=0\)
- \(9y^2−6y+1=0\)
- 回答
-
1。
\(2v^2−3v+6=0\) 方程采用标准形式,标识 a、b、c。 \(a=2\),\(b=−3\),\(c=6\) 写下判别词。 \(b^2−4ac\) 用 a、b、c 的值进行替换。 \((3)^2−4·2·6\) 简化。 \(9−48\)
\(−39\)
由于判别值为负,因此该方程没有真正的解。 2。
\(3x^2+7x−9=0\) 方程采用标准形式,标识 a、b、c。 \(a=3\),\(b=7\),\(c=−9\) 写下判别词。 \(b^2−4ac\) 用 a、b、c 的值进行替换。 \((7)^2−4·3·(−9)\) 简化。 \(49+108\)
\(157\)
由于判别值为正,因此该方程有两个解。 3。
\(5n^2+n+4=0\) 方程采用标准形式,标识 a、b、c。 \(a=5\),\(b=1\),\(c=4\) 写下判别词。 \(b^2−4ac\) 用 a、b、c 的值进行替换。 \((1)^2−4·5·4\) 简化。 \(1−80\)
\(−79\)
由于判别值为负,因此该方程没有真正的解。 4。
\(9y^2−6y+1=0\) 方程采用标准形式,标识 a、b、c。 \(a=9\),\(b=−6\),\(c=1\) 写下判别词。 \(b^2−4ac\) 用 a、b、c 的值进行替换。 \((−6)^2−4·9·1\) 简化。 \(36−36\)
\(0\)
因为判别值为 0,所以方程只有一个解。
确定每个二次方程的解数:
- \(8m^2−3m+6=0\)
- \(5z^2+6z−2=0\)
- \(9w^2+24w+16=0\)
- \(9u^2−2u+4=0\)
- 回答
-
- 没有真正的解决方案
- 2
- 1
- 没有真正的解决方案
确定每个二次方程的解数:
- \( b^2+7b−13=0\)
- \(5a^2−6a+10=0\)
- \(4r^2−20r+25=0\)
- \(7t^2−11t+3=0\)
- 回答
-
- 2
- 没有真正的解决方案
- 1
- 2
确定用于求解二次方程的最合适方法
我们使用了四种方法来求解二次方程:
- 保理
- 平方根属性
- 完成正方形
- 二次方程式
您可以使用二次公式求解任何二次方程,但这并不总是最容易使用的方法。
- 先试试保理。 如果二次因素很容易,则此方法非常快。
- 接下来试试平方根属性。 如果方程符合\(ax^2=k\)或的形式\(a(x−h)^2=k\),则可以使用平方根属性轻松求解。
- 使用二次方程式。 任何二次方程都可以通过使用二次公式求解。
那么完成正方形的方法呢? 大多数人觉得这种方法很麻烦,宁愿不使用它。 我们需要将其包含在本章中,因为我们总体上完成了正方形以得出二次方程式。 你还将在其他代数区域使用完成正方形的过程。
确定用于求解每个二次方程的最合适方法:
- \(5z^2=17\)
- \(4x^2−12x+9=0\)
- \(8u^2+6u=11\)
- 回答
-
1。 \(5z^2=17\)
由于方程在中\(ax^2=k\),因此最合适的方法是使用平方根属性。
2。 \(4x^2−12x+9=0\)
我们认识到,方程的左侧是一个完美的方形三项式,因此分解将是最合适的方法。
3。 \(8u^2+6u=11\)
将方程式以标准形式表示。 \(8u^2+6u−11=0\)
虽然我们首先想到的可能是尝试因子分解,但考虑到所有反复试验的可能性,我们选择二次方程式作为最合适的方法。
确定用于求解每个二次方程的最合适方法:
- \(x^2+6x+8=0\)
- \((n−3)^2=16\)
- \(5p^2−6p=9\)
- 回答
-
- 因素
- 平方根属性
- 二次方程式
确定用于求解每个二次方程的最合适方法:
- \(8a^2+3a−9=0\)
- \(4b^2+4b+1=0\)
- \(5c2=125\)
- 回答
-
- 二次方程式
- 保理
- 平方根属性
访问以下在线资源以获取更多指导和使用二次公式进行练习:
- 求解二次方程:使用二次公式求解
- 如何使用二次公式求解标准形式的二次方程(示例)
- 使用二次公式求解二次方程——示例 3
- 使用二次公式求解二次方程
关键概念
- 二次公式这种形式的\(ax^2+bx+c=0\)二次方程的解由以下公式给出:\(a \ge 0\)
\(x=\frac{−b\pm\sqrt{b^2−4ac}}{2a}\)
- 使用二次公
式求解二次方程使用二次公式求解二次方程。- 以标准形式写出二次公式。 确定 a、b、c 的值。
- 写下二次方程式。 然后用 a、b、c 的值代替。
- 简化。
- 检查解决方案。
- 使用判别法确定二次方程的解数
对于形式的二次方程\(ax^2+bx+c=0\)\(a \ge 0\),\(b^2−4ac\)- if\(b^2−4ac>0\),该方程有 2 个解。
- if\(b^2−4ac=0\),方程有 1 个解。
- if\(b^2−4ac<0\),方程没有实际解。
- 要确定求解二次方程的最合适方法,请执行以下操作:
- 先试试保理。 如果二次因子很容易,则此方法非常快。
- 接下来试试平方根属性。 如果方程符合\(ax^2=k\)或的形式\(a(x−h)^2=k\),则可以使用平方根属性轻松求解。
- 使用二次方程式。 任何其他二次方程最好使用二次公式求解。
词汇表
- 判别的
- 在二次公式\(x=\frac{−b\pm\sqrt{b^2−4ac}}{2a}\)中,量被\(b^2−4ac\)称为判别值。


