10.2:通过完成正方形求解二次方程
- Page ID
- 204498
在本节结束时,您将能够:
- 完成二项式表达式的平方
- \(x^2+bx+c=0\)通过完成正方形求解表格的二次方程
- \(ax^2+bx+c=0\)通过完成正方形求解表格的二次方程
到目前为止,我们已经通过分解和使用平方根属性求解了二次方程。 在本节中,我们将通过一个名为 “完成方程” 的过程求解二次方程。
完成二项式表达式的平方
在最后一节中,我们能够使用平方根属性来求解方程,\((y−7)^2=12\)因为左边是一个完美的正方形。
\[\begin{array}{l} {(y−7)^2=12}\\ {y−7=\pm\sqrt{12}}\\ {y−7=\pm2\sqrt{3}}\\ {y=7\pm2\sqrt{3}}\\ \nonumber \end{array}\]
我们还求解了一个方程,其中左边是一个完美的三项方程,但是\((x−k)^2\)为了使用平方根属性,我们必须将其重写为形式。
\[\begin{array}{l} {x^2−10x+25=18}\\ {(x−5)^2=18}\\ \nonumber \end{array}\]
如果变量不是完美正方形的一部分会发生什么? 我们可以用代数来做一个完美的正方形吗?
让我们研究一下我们多次使用的二项式方形图案。 我们来看两个例子。
\[\begin{array}{ll} {(x+9)^2}&{(y−7)^2}\\ {(x+9)(x+9)}&{(y−7)(y−7)}\\ {x^2+9x+9x+81}&{y^2−7y−7y+49}\\ {x^2+18x+81}&{y^2−14y+49}\\ \nonumber \end{array}\]
如果 a, b 是实数
\((a+b)^2=a^2+2ab+b^2\)
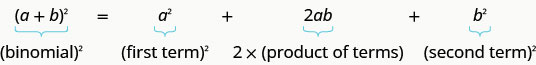
\((a−b)^2=a^2−2ab+b^2\)
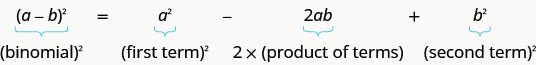
我们可以使用这种图案 “制作” 一个完美的正方形。
我们将从表达式开始\(x^2+6x\)。 由于两个术语之间有一个加号,我们将使用该\((a+b)^2\)模式。
\(a^2+2ab+b^2=(a+b)^2\)
请注意,的第一个项\(x^2+6x\)是正方形\(x^2\)。
我们现在知道了\(a=x\)。
我们可以加什么数字\(x^2+6x\)来构成一个完美的三项方形?
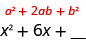
二项式方块图案的中间项 2ab 是二项式两个项的乘积的两倍。 这意味着 x 乘积的两倍,某个数字是 6x。 所以,二倍数必须是六。 我们需要的号码是\(\frac{1}{2}·6=3\)。 二项式中的第二个项 b 必须为 3。
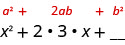
我们现在知道了\(b=3\)。
现在,我们只需对二项式的第二个项进行平方,即可得到完美平方三项式的最后一个项,所以我们求三方得出最后一个项,九个。
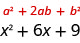
我们现在可以考虑到
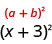
所以,我们发现加九就\(x^2+6x\)是 “完成正方形”,然后我们把它写成\((x+3)^2\)。
要完成以下平方\(x^2+bx\):
- 确定 b,x 的系数。
- 查找\((\frac{1}{2}b)^2\),完成正方形的数字。
- 将添加\( (\frac{1}{2}b)^2\)到\(x^2+bx\)。
完成正方形以形成完美的三项式方形。 然后,将结果写成二项式正方形。
\(x^2+14x\)
- 回答
-
x 的系数为 14。 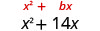
查找\((\frac{1}{2}b)^2\)。
\((\frac{1}{2}⋅14)^2\)
\((7)^2\)
49
在二项式中加 49 以完成正方形。 \(x^2+14x+49\) 重写为二项式方块。 \((x+7)^2\)
完成正方形以形成完美的三项式方形。 将结果写成二项式正方形。
\(y^2+12y\)
- 回答
-
\((y+6)^2\)
完成正方形以形成完美的三项式方形。 将结果写成二项式正方形。
\(z^2+8z\)
- 回答
-
\((z+4)^2\)
完成正方形以形成完美的三项式方形。 然后,将结果写成二项式平方。 \(m^2−26m\)
- 回答
-
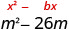
查找\((\frac{1}{2}b)^2\)。
\((\frac{1}{2}⋅(−26))^2\)
\((−13)^2\)
169
向二项式添加 169 以完成正方形。 \(m^2−26m+169\) 重写为二项式方块。 \((m−13)^2\)
完成正方形以形成完美的三项式方形。 将结果写成二项式正方形。
\(a^2−20a\)
- 回答
-
\((a−10)^2\)
完成正方形以形成完美的三项式方形。 将结果写成二项式正方形。
\(b^2−4b\)
- 回答
-
\((b−2)^2\)
完成正方形以形成完美的三项式方形。 然后,将结果写成二项式平方。
\(u^2−9u\)
- 回答
-
u 的系数为 −9。 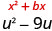
查找\((\frac{1}{2}b)^2\)。
\((\frac{1}{2}⋅(−9))^2\)
\((−\frac{9}{2})^2\)
\(\frac{81}{4}\)
\(\frac{81}{4}\)添加到二项式以完成正方形。 \(u^2−9u+\frac{81}{4}\) 重写为二项式方块。 \((u−\frac{9}{2})^2\)
完成正方形以形成完美的三项式方形。 将结果写成二项式正方形。
\(m^2−5m\)
- 回答
-
\((m−\frac{5}{2})^2\)
完成正方形以形成完美的三项式方形。 将结果写成二项式正方形。
\(n^2+13n\)
- 回答
-
\((n+\frac{13}{2})^2\)
完成正方形以形成完美的三项式方形。 然后,将结果写成二项式平方。
\(p^2+12p\)
- 回答
-
p 的系数为\(\frac{1}{2}\) 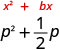
查找\((\frac{1}{2}b)^2\)。
\((\frac{1}{2}⋅\frac{1}{2})^2\)
\((\frac{1}{4})^2\)
\(\frac{1}{16}\)
\(\frac{1}{16}\)添加到二项式以完成正方形。 \(p^2+\frac{1}{2}p+\frac{1}{16}\) 重写为二项式方块。 \((p+\frac{1}{4})^2\)
完成正方形以形成完美的三项式方形。 将结果写成二项式正方形。
\(p^2+\frac{1}{4}p\)
- 回答
-
\((p+\frac{1}{8})^2\)
完成正方形以形成完美的三项式方形。 将结果写成二项式正方形。
\(q^2−\frac{2}{3}q\)
- 回答
-
\((q−\frac{1}{3})^2\)
\(x^2 + bx + c = 0\)通过完成正方形求解表格的二次方程
在求解方程时,我们必须始终对方程的两边做同样的事情。 当然,当我们通过完成方程来求解二次方程时,情况也是如此。 当我们在方程的一侧添加一个项以形成完美的三项方形时,我们还必须将相同的项添加到方程的另一边。
例如,如果我们从方程开始\(x^2+6x=40\),想要完成左边的正方形,我们将在方程的两边加上九个。
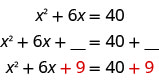
然后,我们在左边考虑因素,在右边进行简化。
\((x+3)^2=49\)
现在,方程采用了使用平方根属性求解的形式。 完成正方形是将方程转换为我们能够使用平方根属性所需的形式的一种方法。
如何\(x^2+bx+c=0\)通过完成正方形来求解形状的二次方程。
\(x^2+8x=48\)通过完成方块来求解。
- 回答
-


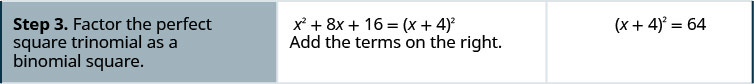



\(c^2+4c=5\)通过完成方块来求解。
- 回答
-
\(c=−5\),\(c=1\)
\(d^2+10d=−9\)通过完成方块来求解。
- 回答
-
\(d=−9\),\(d=−1\)
- 分离一侧的变量项和另一侧的常量项。
- 查找\((\frac{1}{2}·b)^2\),完成正方形的数字。 将其添加到方程的两边。
- 将完美的三项方分解为二项式正方形。
- 使用平方根属性。
- 简化基数,然后求解两个由此产生的方程。
- 检查解决方案。
\(y^2−6y=16\)通过完成方块来求解。
- 回答
-
变量项在左边。 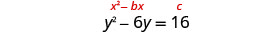
取出 −6 的一半并将其平方。 \((\frac{1}{2}(−6))^2=9\)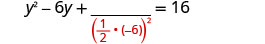
在两边加上 9。 
将完美的三项方分解为二项式正方形。 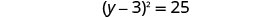
使用平方根属性。 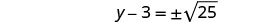
简化激进。 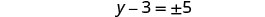
求解 y。 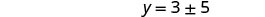
重写以显示两个解决方案。 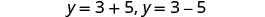
求解方程式。 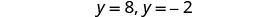
查看。
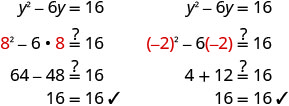
\(r^2−4r=12\)通过完成方块来求解。
- 回答
-
\(r=−2\),\(r=6\)
解决\(t^2−10t=11\) by completing the square.
- 回答
-
\(t=−1\),\(t=11\)
\(x^2+4x=−21\)通过完成方块来求解。
- 回答
-
变量项在左边。 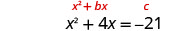
取出 4 的一半并将其平方。 \((\frac{1}{2}(4))^2=4\)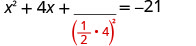
在两边加上 4。 
将完美的三项方分解为二项式正方形。 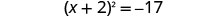
使用平方根属性。 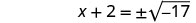
我们不能取负数的平方根。 没有真正的解决办法。
\(y^2−10y=−35\)通过完成方块来求解。
- 回答
-
没有真正的解决方案
\(z^2+8z=−19\)通过完成方块来求解。
- 回答
-
没有真正的解决方案
在前面的示例中,没有真正的解决方案,因为\((x+k)^2\) was equal to a negative number.
\(p^2−18p=−6\)通过完成方块来求解。
- 回答
-
变量项在左边。 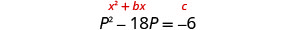
取出 −18 的一半并将其平方。 \((\frac{1}{2}(−18))^2=81\) 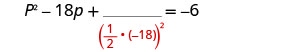
在两边加上 81。 
将完美的三项方分解为二项式正方形。 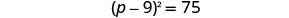
使用平方根属性。 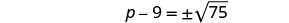
简化激进。 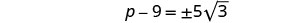
求解 p。 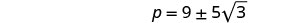
重写以显示两个解决方案。 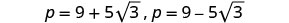
查看。
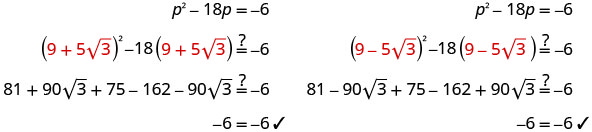
另一种检查方法是使用计算器。 \(p^2−18p\)评估这两种解决方案。 答案应为 −6。
\(x^2−16x=−16\)通过完成方块来求解。
- 回答
-
\(x=8\pm4\sqrt{3}\)
\(y^2+8y=11\)通过完成方块来求解。
- 回答
-
\(y=−4\pm3\sqrt{3}\)
我们将从隔离方程左侧的变量项开始下一个示例。
\(x^2+10x+4=15\)通过完成方块来求解。
- 回答
-
变量项在左边。 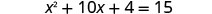
减去 4 得到右侧的常量项。 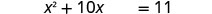
取出 10 分的一半然后将其平方。 \((\frac{1}{2}(10))^2=25\)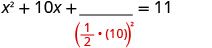
在两边加上 25。 
将完美的三项方分解为二项式正方形。 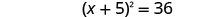
使用平方根属性。 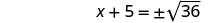
简化激进。 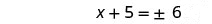
求解 x。 
重写以显示两个方程。 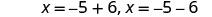
求解方程式。 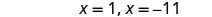
查看。
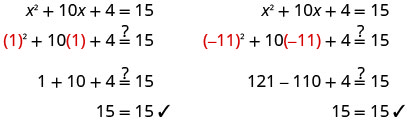
\(a^2+4a+9=30\)通过完成方块来求解。
- 回答
-
\(a=−7\),\(a=3\)
解决\(b^2+8b−4=16\) by completing the square.
- 回答
-
\(b=−10\),\(b=2\)
要求解下一个方程,我们必须首先收集方程左侧的所有变量项。 然后,我们按照前面的示例进行操作。
\(n^2=3n+11\)通过完成方块来求解。
- 回答
-
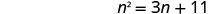
减去 3 n 得到左侧的变量项。 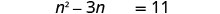
取出 −3 的一半并将其平方。 \((\frac{1}{2}(−3))^2= \frac{9}{4}\) 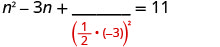
两\(\frac{9}{4}\)边都加上。 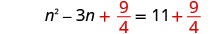
将完美的三项方分解为二项式正方形。 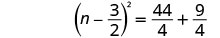
在右侧添加分数。 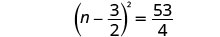
使用平方根属性。 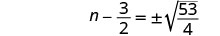
简化激进。 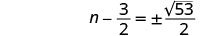
求解 n。 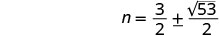
重写以显示两个方程。 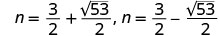
查看。 我们把支票留给你!
\(p^2=5p+9\)通过完成方块来求解。
- 回答
-
\(p=\frac{5}{2}\pm\frac{\sqrt{61}}{2}\)
解决\(q^2=7q−3\) by completing the square.
- 回答
-
\(q=\frac{7}{2}\pm\frac{\sqrt{37}}{2}\)
请注意,下一个方程的左侧是因子形式。 但是右边不是零,所以我们不能使用零积属性。 取而代之的是,我们将因子相乘,然后将方程转换为标准形式,通过完成方程来求解。
\((x−3)(x+5)=9\)通过完成方块来求解。
- 回答
-
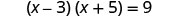
我们在左边乘以二项式。 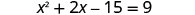
加 15 以获得左侧的变量项。 
取出 2 的一半并将其平方。 \((\frac{1}{2}(2))^2=1\)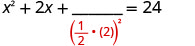
在两边加上 1。 
将完美的三项方分解为二项式正方形。 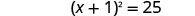
使用平方根属性。 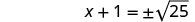
求解 x。 
重写以显示两个解决方案。 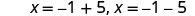
简化。 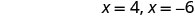
查看。 我们把支票留给你!
\((c−2)(c+8)=7\)通过完成方块来求解。
- 回答
-
\(c=−3\pm4\sqrt{2}\)
\((d−7)(d+3)=56\)通过完成方块来求解。
- 回答
-
\(d=−7\),\(d=11\)
\( ax^2 + bx + c = 0\)通过完成正方形求解表格的二次方程
当前导系数为 1 时,完成正方形的过程效果最好,因此方程左侧的形式为\(x^2+bx+c\)。 如果该\(x^2\)项有系数,我们采取一些初步步骤使该系数等于一。
有时,系数可以从三项式的所有三个项中分解出来。 这将是我们在下一个例子中的策略。
\(3x^2−12x−15=0\)通过完成方块来求解。
- 回答
-
要完成平方,我们需要将的系数\(x^2\)设为一。 如果我们将的系数\(x^2\)作为公因子分解,我们可以通过完成方程来继续求解方程。
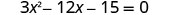
排除最大的共同因素。 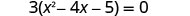
将两边除以 3 以隔离三项式。 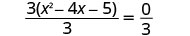
简化。 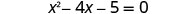
减去 5 得到右边的常量项。 
取出 4 的一半并将其平方。 \((\frac{1}{2}(4))^2=4\)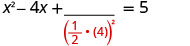
在两边加上 4。 
将完美的三项方分解为二项式正方形。 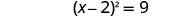
使用平方根属性。 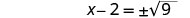
求解 x。 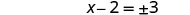
重写以显示 2 个解决方案。 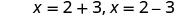
简化。 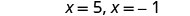
查看。
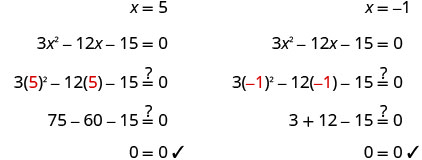
\(2m^2+16m−8=0\)通过完成方块来求解。
- 回答
-
\(m=−4\pm2\sqrt{5}\)
\(4n^2−24n−56=8\)通过完成方块来求解。
- 回答
-
\(n=−2, 8\)
要完成平方,前导系数必须为一。 当前导系数不是所有项的因子时,我们将把方程的两边除以前导系数。 这将为我们提供第二个系数的分数。 在本节中,我们已经看到了如何用分数完成正方形。
\(2x^2−3x=20\)通过完成方块来求解。
- 回答
-
同样,我们的第一步将是将的系数设\(x^2\)为一。 通过将方程的两边除以系数\(x^2\),然后我们可以通过完成方程来继续求解方程。
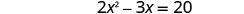
将两边除以 2 得\(x^2\)到 1 的系数。 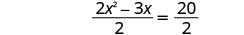
简化。 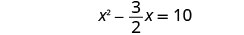
取一半\(−\frac{3}{2}\)然后把它弄成平方。 \((\frac{1}{2}(−\frac{3}{2}))^2=\frac{9}{16}\)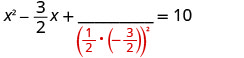
两\(\frac{9}{16}\)边都加上。 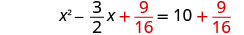
将完美的三项方分解为二项式正方形。 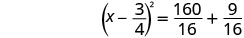
在右侧添加分数。 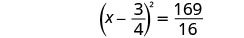
使用平方根属性。 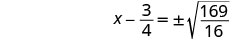
简化激进。 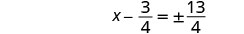
求解 x。 
重写以显示 2 个解决方案。 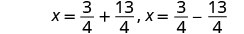
简化。 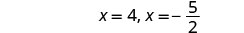
查看。 我们把支票留给你。
\(3r^2−2r=21\)通过完成方块来求解。
- 回答
-
\(r=−\frac{7}{3}\),\(r=3\)
\(4t^2+2t=20\)通过完成方块来求解。
- 回答
-
\(t=−\frac{5}{2}\),\(t=2\)
\(3x^2+2x=4\)通过完成方块来求解。
- 回答
-
同样,我们的第一步将是将的系数设\(x^2\)为一。 通过将方程的两边除以系数\(x^2\),然后我们可以通过完成方程来继续求解方程。
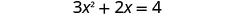
将两边除以 3 使系数\(x^2\)等于 1。 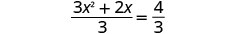
简化。 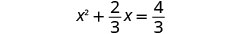
取一半\(\frac{2}{3}\)然后把它弄成平方。 \((\frac{1}{2}⋅\frac{2}{3})^2=\frac{1}{9}\)
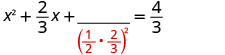
两\(\frac{1}{9}\)边都加上。 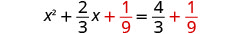
将完美的三项方分解为二项式正方形。 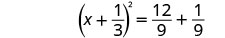
使用平方根属性。 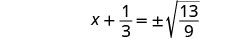
简化激进。 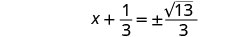
求解 x。 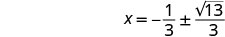
重写以显示 2 个解决方案。 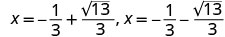
查看。 我们把支票留给你。
\(4x^2+3x=12\)通过完成方块来求解。
- 回答
-
\(x=−\frac{3}{8}\pm\frac{\sqrt{201}}{8}\)
\(5y^2+3y=10\)通过完成方块来求解。
- 回答
-
\(y=−\frac{3}{10}\pm\frac{\sqrt{209}}{10}\)
访问以下在线资源,获取更多指导和练习,通过完成方程求解二次方程:
- 完成正方形的方法简介
- 如何通过完成方块来求解
关键概念
- 二项式正方形图案如果 a、ba、b 是实数,
\((a+b)^2=a^2+2ab+b^2\)
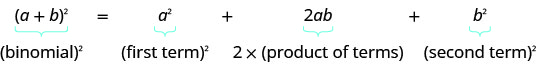
\((a−b)^2=a^2−2ab+b^2\)
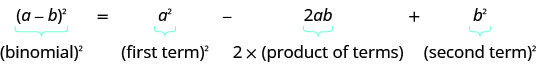
- 完成一个正方形
要完成以下正方形\(x^2+bx\):- 识别 bb,x 的系数。
- 查找\((\frac{1}{2}b)^2\),完成正方形的数字。
- 将添加\((\frac{1}{2}b)^2\)到\(x^2+bx\)。
词汇表
- 完成正方形
- 完成方程是一种用于求解二次方程的方法。


